Introduction

The hydrologic system is essentially a nonlinear system which is sensitive to the heterogeneity of input and processes. Numerous studies have explored the sensitivity of hydrologic response to the spatial–temporal variability of rainfall, antecedent soil moisture, surface and subsurface processes of runoff generation and the flow routing (Robinson et al. 1995; Singh 1997; Koren et al. 1999; Arora et al. 2001; Famiglietti et al. 2008; Huang et al. 2014; Lázaro et al. 2014; Mateo Lázaro et al. 2014; McMillan et al. 2014). All these studies show the importance of spatial–temporal patterns on the hydrologic response. Nowadays, the development of distributed rainfall–runoff models, especially the physically based small-scale processes models, combined with more and more distributed input data and verification information provided by remote sensing (RS), Geographic Information Systems (GIS), leads to significant advances in the accurate representation of spatial–temporal varying field.

However, more recent researches suggest that with the abundant data, the distributed modeling approaches may not always provide improved outlet simulations compared to the lumped conceptual models (Reed et al. 2004; Smith et al. 2004). One of the underlying causes for this is the overparameterization of the distributed model (Beven 1999). The problem of overparameterization not only leads the difficulty in parameter identifying, but also causes the problem of equifinality (Mazzilli et al. 2013). Therefore, the issues of how to avoid excessive model complexity have become a focus in recent research (Sivapalan 2003; Sivakumar 2004; Blöschl et al. 2008). Grayson and Blöschl (2001) proposed the dominant process concept which calls for the new methods to identify the dominant processes in different scales and environments. They pointed out that the current distributed models usually gather more and more data and involve many processes that try to ‘model everything’, but the fact is that only a few processes dominant hydrologic response in a specific catchment. The processes important at one scale may not necessarily be important at others, larger or smaller scales (Blöschl and Sivapalan 1995; Sivapalan 2003). Therefore, not all the processes are required to be embedded for the hydrologic modeling at certain scale. In view of these, the quantitative evaluation of the different hydrologic processes at varying scales and environments is needed to “capture the essential features” of a given catchment’s response (Sivakumar 2004). This analysis can also provide a useful guidance in selecting appropriate model structures and complexity, for particular modeling needs (Woods 2002).

To address this, several attempts have been made by analyzing the contribution of different processes to the hydrologic response. Robinson et al. (1995) and D’Odorico and Rigon (2003) analyzed the relative role of the hillslope and the channel routing at a range of scales. They both suggested that the hillslope governs the hydrologic response in the small basin, and the importance of channel routing increases with the catchment size. Woods and Sivapalan (1999) proposed an analytical variability framework to quantify the contribution of rainfall excess, runoff and flow routing on the flood response, which gives insight into the complex interactions among the key variables affecting the flood response. Based on their works, Viglione et al. (2010a) extended the variability framework by relaxing two of the most restrictive assumptions: (1) the multiplicative space–time separability for both the rainfall and the runoff generation processes; (2) the spatially uniform distribution of the hillslope travel time. Arnaud et al. (2002) thought that the relative role of the spatial variability becomes more significant for the larger catchment due to the spatial variability increasing with the catchment size. Western et al. (2004) summarized the spatial correlation of soil moisture and discussed its relationship to the dominant spatial hydrologic processes. McMillan et al. (2014) illustrate various threshold controls in the response of karst aquifers by the tracer test data. For a comprehensive review see McDonnell et al. (2007) and Sivakumar et al. (2007).

The main scope of this paper is to assess the effect of spatial variability of rainfall and flow routing on the hydrologic response. The variability framework presented by Viglione et al. (2010a) is adopted to quantify the contribution of variability to the main features of hydrograph (order of magnitude of flood, time to peak and dispersion of hydrograph). A set of experiments is designed and carried out at the Yanduhe Basin and its 64 subcatchments, to explore the sensitivity of hydrologic response to the spatial variability at different scales. For a more general conclusion, a stochastic rainfall generator is selected to reproduce the local rainfall structure. The hillslope or channel dominance on shaping the hydrograph is also investigated at varying flow velocity and catchment size conditions. The understanding of relative role of hillslope and channel on the hydrologic response would be of benefit to our modeling strategy by capturing the essential processes.

Study area

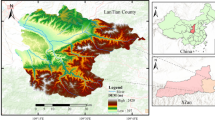
This study is performed at the Yanduhe Basin, which locates in the central China with a catchment area of about 636 km2. The Yanduhe River, the main river of Yanduhe Basin, originating from south of Shennongjia Mountain, flowing into Yangtze River at 31°14′N, 110°18′E, is 60.6 km in length with a mean slope of 9.5 ‰. More than 70 % of the area is covered by vegetation. The watershed climate is humid, and the average annual precipitation is about 1300–1700 mm. As shown in Fig. 1, the rainfall is monitored at five rainfall gauging stations, located in Duizi, Xiagu, Banqiao, Songziyuan and Yanduhe, respectively. Hourly streamflow data is recorded at the outlet of the watershed. The morphology of basin is described by the Digital Elevation Models (DEMs) with 100 m resolution, ranging from 130 to 3031 m. The soil texture data comes from the Harmonized World Soil Dataset of Food and Agriculture Organization (China region, 30 in. resolution). To assess the effect of the spatial variability contribution at different scales, 64 subcatchments are subdivided from the Yanduhe Basin by the seeding technique (Jenson and Domingue 1988). The area of subcatchment ranges from 1 to 636 km2.

Fig. 1
figure 1

Location of the Yanduhe Basin

Full size image

Methodology

Variability framework

The variability framework (called VF model hereinafter) presented by Viglione et al. (2010a) characterizes the flood response in a rainfall event with three quantities: (1) the catchment- and storm-averaged rainfall excess; (2) the mean catchment runoff time; and (3) the variance of the catchment runoff time. They are all expressed in terms of spatial–temporal variability of rainfall, runoff and flow routing with accounting for the interactions of these processes. With these three quantities, the order of magnitude of flood, time to peak and dispersion in time can be roughly estimated. Instead of accurate hydrologic simulation, the aim of VF model is to identify the dominant source of variability. The VF model is a substantial simplification of reality, which can be summarized as: rainfall field transforms to the rainfall excess by a distributed rainfall–runoff model, then rainfall excess is routed to the catchment outlet with a given flow time field. Figure 2 shows a schematic diagram of the VF model. Here, only some basic equations are presented; for more details of the VF model see Viglione et al. (2010a).

Fig. 2
figure 2

Schematic diagram of the VF model

Full size image

Catchment and storm-averaged rainfall excess

In the VF model, the catchment and storm-averaged rainfall excess reflects the order of magnitude of flood in a rainfall event. To explicitly express the effect of the spatial–temporal rainfall and soil moisture state, the rainfall excess \(R(x,y,t)\) [L T −1] at time t and at point (x, y) can be thought as the product of rainfall field \(P(x,y,t)\) [L T −1] is runoff coefficient \(W(x,y,t)\) [–]. In this study, the runoff coefficient \(W(x,y,t)\) is estimated by the Grid-XAJ model (Liu et al. 2009; Yao et al. 2012), which is a distributed hydrologic model widely used in humid and semi-humid area of China. The catchment- and storm-averaged rainfall excess \(R_{xyt}\) [L T −1] can be computed by integrating the rainfall excess \(R(x,y,t)\) in time and space domain:

$$\begin{aligned} R_{xyt} \; = \underbrace {{P_{xyt} \cdot W_{xyt} }}_{R1} + \underbrace {{\text{cov} (P_{xy} (t),W_{xy} (t))}}_{R2} + \underbrace {{\text{cov} (P_{t} \left( {x,y} \right),W_{t} \left( {x,y} \right))}}_{R3} \hfill \\ + \underbrace {{[\text{cov} (P\left( {x,y,t} \right) - P_{xy} (t),W\left( {x,y,t} \right) - W_{xy} (t))]_{xy} }}_{R4}, \hfill \\ \end{aligned}$$
(1)

where \(T_{\text{m}}\) [T] and \(A\) [L 2] are the rainfall duration and the catchment area, \(P_{xyt}\) [L T −1] and \(W_{xyt}\) [–] are the time-averaged catchment-averaged rainfall rates and runoff coefficient, \(P_{xy} (t)\) [L T −1] and \(W_{xy} (t)\) [–] are time series of catchment-averaged rainfall rates and runoff coefficient, \(P_{t} (x,y)\) [L T −1] and \(W_{t} (x,y)\) [–] are the map of the temporally averaged rainfall rates and runoff coefficient, the operator \([ \cdot ]_{xy}\) indicates the spatial averages. In Eq. 1, the catchment- and storm-averaged rainfall excess consists of four terms: \(R1\) represents the contribution of the mean precipitation and runoff coefficient on the rainfall excess, \(R2\) represents the contribution caused by the temporal variability of precipitation and runoff coefficient, \(R3\) represents the contribution caused by the spatial variability of precipitation and runoff coefficient, \(R4\) is a product that accounts for the spatial variation in temporal covariance.

Mean catchment runoff time

For purpose of estimating the runoff time, the VF model defines three stages for a raindrop from the start of the rainfall event to the outlet of watershed: (1) the time for the raindrop falls on the ground from the start of rainfall event \(T_{\text{r}} (x,y)\) [T]; (2) the time of hillslope routing \(T_{\text{h}} (x,y)\) [T]; (3) the time of channel routing \(T_{\text{n}} (x,y)\) [T]. Among them, \(T_{\text{r}} (x,y)\) mainly depends on the characteristic of the rainfall event, so it will not be discussed here. Hence, the total resident time of the raindrop \(T_{\text{q}} (x,y)\) [T] in a rainfall event can be simplified as: \(T_{\text{q}} = T_{\text{h}} + T_{\text{n}}\). According to the mass conservation law, the mean catchment runoff time can be derived as:

$$E(T_{\text{q}} ) = E(T_{\text{h}} ) + E(T_{\text{n}} ).$$
(2)

In more detail, Eq. 2 can be written as:

$$E\left( {T_{\text{h}} } \right) = \underbrace {{[T_{\text{h}} ]_{xy} }}_{{E{\text{h1}} }} + \underbrace {{\frac{{Cov(T_{\text{h}} ,R_{t} (x,y))}}{{R_{xyt} }}}}_{{E{\text{h2}} }}$$
(3)
$$E\left( {T_{{\text{h}}} } \right) = \underbrace {{[T_{{\text{h}}} ]_{{xy}} }}_{{E{\text{n1}}}} + \underbrace {{\frac{{Cov(T_{{\text{h}}} ,R_{t} (x,y))}}{{R_{{xyt}} }}}}_{{E{\text{n2}}}}$$
(4)

where \([T_{\text{h}} ]_{xy}\) [T] is the spatially averaged hillslope travel time, \([T_{\text{n}} ]_{xy}\) [T] is spatially averaged channel travel time, \(R_{t}\) [L T −1] is the map of temporally averaged rainfall excess. \(E\text{h}1\) and \(E\text{n}1\) explain the contribution of catchment-averaged hillslope and channel routing on the mean runoff time. \(E\text{h}2\) and \(E\text{n}1\) result from the contribution of spatial variability with accounting for the spatial interaction of runoff and hillslope or channel routing time.

Variance of catchment runoff time

The variance of catchment runoff time is the measurement of dispersion of hydrograph. It can be expressed as the sum of variance in hillslope and channel routing. There are some covariance terms caused by the relaxation of the separability assumption, which account for the additional variance, resulting from the correlation among these processes. But considering that there is no direct correlation between the runoff and flow routing time, and the covariance terms are one or two order of magnitude less than the variance term (Viglione et al. 2010b), we ignore the effect of the covariance terms in this study. Thus the variance of catchment runoff time simplifies to:

$${\text{Var}}(T_{\text{q}} ) = {\text{Var}}(T_{\text{h}} ) + {\text{Var}}(T_{\text{n}} ).$$
(5)

In more detail:

$${\text{Var}}(T_{\text{h}} ) = \underbrace {{{\text{Var}}(T_{\text{h}} )}}_{\text{Vh1}} + \underbrace {{\frac{{{\text{Cov(}}T_{\text{h}}^{2} ,R_{t} (x,y))}}{{R_{xyt} }} - \frac{{{\text{Cov}}(T_{\text{h}} ,R_{t} )}}{{R_{xyt} }}\left[ {2[T_{\text{h}} ]_{xy} + \frac{{{\text{Cov}}(T_{\text{h}} ,R_{t} (x,y))}}{{R_{xyt} }}} \right]}}_{\text{Vh2}}$$
(6)
$${\text{Var}}(T_{\text{n}} ) = \underbrace {{{\text{Var}}(T_{\text{n}} )}}_{\text{Vn1}} + \underbrace {{\frac{{{\text{Cov}}(T_{\text{n}}^{2} ,R_{t} (x,y))}}{{R_{xyt} }} - \frac{{{\text{Cov}}(T_{\text{n}} ,R_{t} )}}{{R_{xyt} }}\left[ {2[T_{\text{n}} ]_{x,y} + \frac{{{\text{Cov}}(T_{\text{n}} ,R_{t} (x,y))}}{{R_{xyt} }}} \right]}}_{\text{Vn2}}$$
(7)

where \({\text{Vh1}}\) is the variance of hillslope routing time, \({\text{Vh2}}\) is the additional variance caused by the spatial variability of rainfall excess and hillslope routing, \({\text{Vn1}}\) is the variance of channel routing time, \({\text{Vn2}}\) is the additional variance caused by the spatial variability of rainfall excess and channel routing.

Stochastic rainfall field

To avoid the conclusion affected by a specific rainfall event, a stochastic rainfall generator (Over and Gupta 1996; Kang and Ramírez 2010) is selected to provide the rainfall field \(P(x,y,t)\) as input of the VF model. This stochastic rainfall generator allows the hourly rainfall intensities to be capable of preserving the small-scale dependency characteristics. Moreover, it can also ensure the consistency of rainfall characteristic for the comparison across scale. For the purpose of this paper, the areal-averaged rainfall intensity is assumed to be temporally uniform. Then the areal-averaged rainfall intensity is extended to spatial–temporal distribution by a random cascade generator, which assumes the spatial rainfall field is independent and identically distributed (iid) random variables and has a self-similar property.

For the stochastic rainfall generator, three characteristics of rainfall needs to be specified: (1) rainfall duration; (2) total volume of rainfall event; (3) correlation length of rainfall. We perform an analysis to identify the statistical properties of rainfall events at the Yanduhe Basin. Figure 3 shows the analysis results derived from the measured rainfall data from 1996 to 1999. The rainfall duration is defined as the duration of consecutive time recorded at the rainfall gauging stations. The spatial correlation length of rainfall is estimated by the Pearson’s correlation coefficient. Based on the data analysis, the 24-h rainfall duration is selected as the mean of rainfall duration distribution for a rainfall event at the Yanduhe Basin. The spatial correlation length of rainfall field is about 60 km. Figure 4 provides an example of spatial cumulative rainfall field in 24 h with the rainfall intensity of 1 mm/h and the spatial correlation of 60 km.

Fig. 3
figure 3

Rainfall characteristics analysis for the Yanduhe Basin. a The cumulative distribution function (CDF) of rainfall volume. b The CDF of rainfall duration. c The spatial correlation function

Full size image
Fig. 4
figure 4

One example of spatial cumulative rainfall field

Full size image

Antecedent soil moisture

Numerous studies have suggested that the spatial organization of soil moisture is a crucial factor for the hydrologic processes (Goodrich et al. 1994; Western et al. 2004; Vivoni et al. 2009). To obtain a reasonable distribution of antecedent soil moisture, we run a drainage experiment presented by Vivoni et al. (2007), which assumes that the spatial distribution of soil moisture is controlled by the watershed topography. According to the drainage experiment, the watershed starts to drain from a fully saturated status without rainfall and evapotranspiration. The watershed outflux is controlled by the hydraulic gradient. The drainage process stops until the watershed reaches the soil condition we choose. The antecedent soil moisture is used as input of Grid-XAJ model for computing the runoff coefficient \(W(x,y,t)\). In Fig. 5, we show the spatial distribution of soil moisture when the watershed-averaged soil moisture \(\theta\) is 0.8, 0.5 and 0.2, corresponding to the wet, intermediate and dry conditions.

Fig. 5
figure 5

An illustration of the spatial distribution of antecedent soil moisture for the wet, medium and dry conditions

Full size image

Flow routing time

In the VF mode, determining the travel time requires the specification of flow path and velocity for each grid. The flow path is automatically extracted from DEM by ArcGIS. The original VF model adopts the uniform flow velocity hypothesis. Thus, the flow routing is modeled as function of flow velocity in hillslope \(V_{\text{h}}\) and channel \(V_{\text{c}}\). As discussed by Maidment et al. (1996), the flow velocity in hillslope or channel is spatially uneven and highly related to the basin morphology. To explore the effect of the heterogeneity of the flow routing, the spatially uniform flow velocity in the VF model is replaced by a spatially distributed flow velocity. The flow velocity in each grid can be estimated as:

$$V = \frac{{V_{\text{mean}} }}{{[S^{b} A^{c} ]_{\text{mean}} }}S^{b} A^{c} ,$$
(8)

where \(V_{\text{mean}}\) [L T −1] is the watershed average flow velocity in hillslope or channel, \(S\) [–] is the slope in each grid, \(A\) [L 2] is the corresponding upstream drainage area, \(b\) and \(c\) are model parameters.

Results and discussion

Model evaluation

The model evaluation is necessary to ensure the reliability of the VF model prior to the quantitative analysis. For the parameters of the Grid-XAJ model refer to Yao et al. (2012). The flow velocity in hillslope and channel are calibrated by four flood events during 1996–1999 at hourly time step. The precipitation comes from the interpolation of rainfall observation at all five rainfall gauging stations by the inverse distance weighting method. In the VF model, the hydrograph at the outlet of the watershed can be obtained by integrating of product of runoff and travel time in time and space. The Nash–Sutcliffe efficiency coefficient (NSE) is used as the objective function for calibration. We compare the relative error of rainfall excess REr and peak flow REp, the error of time to peak E t in each flood event. The results are summarized in Table 1. It can be seen that due to the some simplification used in the VF model, there remain some errors between the simulation and observation. However, it needs to be noted that the objective of the VF model is to provide insight into the relative importance of spatial–temporal variability, rather than the accurate prediction. The mean NSE of four rainfall events is approximately 0.82, which can be accepted for the following analysis.

Table 1 Performance of the VF model at the Yanduhe Basin
Full size table

Effect of spatial variability of rainfall on rainfall excess

The different spatial–temporal patterns of rainfall and catchment characteristics often lead to the different partitioning of rainfall. According to the VF model, the catchment- and storm-averaged rainfall excess \(R_{xyt}\) is expressed as the sum of the product of time and catchment-averaged rainfall and runoff coefficient (\(R1\)), the temporal and spatial covariance of rainfall and runoff coefficient field (\(R2\), \(R3\) and \(R4\)). Among them, \(R3\) measures the rainfall excess resulting from the spatial variability of rainfall and runoff coefficient. Therefore, the relative contribution of spatial variability of rainfall on the rainfall excess in the rainfall event can be estimated as \(\lambda_{\text{r}} = \left| {R3/R_{xyt} } \right|\). \(\lambda_{\text{r}}\) reflects the relative importance of spatial variability on the estimation of the total rainfall excess.

The rainfall excess in rainfall event is highly dependent on the characteristics of rainfall and antecedent soil moisture (Gabellani et al. 2007; Paschalis et al. 2014). In the first set of experiment, we explore the sensitivity of rainfall excess to spatial variability of rainfall at varying rainfall intensity \(i\). 300 rainfall events are simulated by the stochastic rainfall generator as input of the VF model. The rainfall intensity \(i\) is selected to range from 0.01 to 2.0 mm/h, so as to match with most of the possible total rainfall volume during 24 h at the Yanduhe Basin. The antecedent soil moisture \(\theta\) is assigned a fixed value of 0.5. Figure 6a depicts \(\lambda_{\text{r}}\) as function of the rainfall intensity \(i\). It is observed that the scatter exhibits a convex upward trend. The impact of spatial variability of rainfall is most prominent when \(i\) lies within the range of 0.1–1.0 mm/h. For the Yanduhe Basin, \(\lambda_{\text{r}}\) can attain around 0.2 when the rainfall intensity \(i\) is about 0.25 mm/h. It means that the error of runoff volume estimation can be as high as 20 % if the spatial variability of rainfall is not well represented or only the catchment-averaged rainfall and catchment information is available. When the rainfall is extremely small or larger than 1.0 mm/h, the effect of spatial variability of rainfall is almost negligible. This is because in the case of the drizzle condition, the rainfall volume is too small to cause the runoff generation for the saturation excess mechanism employed by the Grid-XAJ model; while for the rainfall intensity \(i\) larger than 1.5 mm/h, most area of the watershed will reach saturation over a period of time. After that, wherever the raindrop falls on, it will convert into the runoff directly without loss. In this case, the effect of spatial variability of rainfall on the total rainfall excess only depends on the distribution of antecedent water deficit.

Fig. 6
figure 6

Effect of spatial variability of rainfall on the rainfall excess in varying rainfall intensity and antecedent soil moisture

Full size image

In Fig. 6b, we plot the relationship between \(\lambda_{\text{r}}\) and antecedent soil moisture \(\theta\). In this set of simulations, \(\theta\) varies from 0 to 1, while the rainfall intensity \(i\) keeps constant at 0.5 mm/h. We note that the relationship between \(\lambda_{\text{r}}\) and \(\theta\) exhibits a similar pattern as that between \(\lambda_{\text{r}}\) and \(i\). The only difference is that the effect of spatial variability of rainfall is still marked when the antecedent soil moisture is extremely dry. The peak value of \(\lambda_{\text{r}}\) appears when the antecedent soil moisture \(\theta\) is around 0.2. In this case, the spatial variability of rainfall contributes around 18 % of the total rainfall excess. After that, \(\lambda_{\text{r}}\) gradually goes down as \(\theta\) rises. From Fig. 5, it can be observed that the saturated areas reduce rapidly from wet to dry antecedent condition, especially for the areas far from riparian. Compared to the wet soil condition, the variance of soil moisture in the dry condition fluctuates in a larger range. The variance of antecedent water deficit reaches maximum when \(\theta\) is around 0.2. With increasing of antecedent soil moisture, more areas get saturated in this rainfall intensity. Therefore, the effect of spatial variability of rainfall starts to drop. The trend is similar for larger or smaller rainfall intensity, and the upper limit of \(\lambda_{\text{r}}\) will vary as a function of rainfall intensity \(i\) and antecedent soil moisture \(\theta\). These results are in line with Famiglietti et al. (2008).

To investigate how the effect of the spatial variability contribution changes with catchment size, we plot averaged \(\lambda_{\text{r}}\) from all the rainfall events at each subcatchment against the catchment size (Fig. 7). Both the rainfall intensity and the antecedent soil moisture use a fixed value of 0.5 mm/h and 0.5, respectively. It can be seen that \(\lambda_{\text{r}}\) increases with the catchment size. For the small catchment (<10 km2), the spatial variability of rainfall contributes less than 10 % of the total rainfall excess on average. With increase of catchment size, the significance of spatial variability of rainfall increases. For the large catchment (>100 km2), \(\lambda_{\text{r}}\) is almost two or three times than that of the small catchment. This result can be explained by the fact that the spatial correlation of stochastic rainfall is larger than all the subcatchment sizes. For the 60 km spatial correlation length, the variance of spatial rainfall field will keep increasing with the catchments area. However, once the catchment size is larger than the spatial correlation length of rainfall, the spatial variability of rainfall may be filtered as the high-frequency component. Then \(\lambda_{\text{r}}\) will go down with the increase of catchment size.

Fig. 7
figure 7

Effect of spatial variability of rainfall on the rainfall excess for variety of catchment size at the Yanduhe Basin

Full size image

Effect of spatial variability of flow routing on runoff time

The spatial difference of flow routing velocity is another source of variability in the hydrologic processes. The spatial distribution of flow routing velocity is related to the basin morphology, the land cover, etc. Especially for the hillslope routing, the flow velocity is also affected by the preferential flow path (e.g., surface, subsurface and groundwater flow). The flow velocity in the hillslope may present a large difference between fast and slow runoff dominant condition. In the hillslope stage, the flow velocity varies from 0.001 to 0.1 m/s; while in the channel stage, the flow velocity mainly fluctuates between 0.5 and 4 m/s (D’Odorico and Rigon 2003; Hardie et al. 2013). As discussed by Botter and Rinaldo (2003) and Nicótina et al. (2008), the feature of hydrograph is controlled by the flow velocity ratio of hillslope and channel \(V_{\text{h}} /V_{\text{c}}\). Equation 8 is adopted to compute the spatial distribution of flow velocity in hillslope and channel caused by the basin morphology. The watershed average flow velocity in the channel \(V_{\text{c}}\) is assigned as 1 m/s, and the watershed average flow velocity in the hillslope \(V_{\text{h}}\) varies from 0.005 to 0.1 m/h, which corresponds to the runoff response pattern from slow to fast. The VF model measures the contribution of spatial variability of hillslope and channel routing to the time to peak and the dispersion of hydrograph by \({\text{ETh}}\), \({\text{ETn}}\), \({\text{VTh}}\) and \({\text{VTn}}\), respectively. In this section, we explore the hillslope and channel dominance on shaping of hydrograph by computing the ratio of \({\text{ETh}}/{\text{ETn}}\) and \({\text{VTh/}}{\mkern 1mu} {\text{VTn}}\). The same stochastic rainfall field and antecedent soil moisture condition is used as mentioned in the previous section. Figure 8 depicts \({\text{ETh}}/{\text{ETn}}\) and \({\text{VTh/}}{\mkern 1mu} {\text{VTn}}\) as function of the flow velocity ratio \(V_{\text{h}} /V_{\text{c}}\). We can see that the hillslope routing is predominant for slow runoff. When the flow velocity ratio \(V_{\text{h}} /V_{\text{c}}\) is less than 0.04, the mean travel time in the hillslope is large than that in the channel. Due to the relatively short travel time in the channel, the contribution of channel routing to the dispersion of hydrology is also very limited. However, when the flow velocity ratio \(V_{\text{h}} /V_{\text{c}}\) is larger than 0.04, the averaged travel time in the channel already exceeds that in the hillslope. With the growth of runoff response velocity, the dominance of hillslope routing is gradually replaced by the channel routing.

Fig. 8
figure 8

Relative contribution of hillslope and channel to a the time to peak, and b the dispersion of hydrograph in varying velocity ratio

Full size image

The catchment size is another issue we need to consider when we evaluate the relative role of hillslope and channel. To investigate this issue, we extend our analysis to all the subcatchments with fixed flow velocity ratio as 0.05. In Fig. 9, the averaged \({\text{ETh}}/{\text{ETn}}\) and \({\text{VTh/}}{\mkern 1mu} {\text{VTn}}\) from all the rainfall events are plotted against the catchment size. It is observed that the hillslope routing is dominant for the relatively small catchments. For the catchments smaller than 10 km2, the average travel time in the hillslope is 2–10 times than that in the channel (Fig. 9a). With the increase of catchment size, the contribution of channel routing to the average runoff time gradually becomes marked. For all the subcatchments at the Yanduhe Basin, the mean hillslope length do not have obvious change. But the channel length significantly increases with catchment size. For the catchment larger than 100 km2, the average channel time has the same order of magnitude as the travel time in the hillslope routing. It can be concluded that in the case of small catchment or slow runoff condition, it is more important to provide an accurate representation of the spatial variability of hillslope to obtain a realistic hydrologic response; while for large catchment or fast runoff, the effect of channel routing is more significant.

Fig. 9
figure 9

Relative contribution of hillslope and channel to a the time to peak and b the dispersion of hydrograph in varying catchment size

Full size image

Conclusion

In this study, we seek to assess the effect of spatial variability of rainfall and flow routing on the hydrologic response in the rainfall event. The analysis is based on the VF model, which explicitly expresses the contribution of spatial–temporal variability of rainfall, runoff generation and flow routing to the main features of hydrograph. A set of experiments is carried out at the Yanduhe Basin and its 64 subcatchment, with the area ranging over 3 orders of magnitude, to explore the relationship between the sensitivity of hydrologic response and the spatial variability of rainfall and flow routing. To obtain a more general conclusion, a stochastic rainfall generator is selected to reproduce the local rainfall structure as input of the VF model.

The results of this numerical experiment suggest that the dependence of the total rainfall excess on the spatial rainfall variability varies with rainfall and antecedent soil moisture condition. The rainfall excess is the most sensitive to the spatial variability of rainfall in the case of relatively small rainfall intensity or antecedent dry condition. For the Yanduhe Basin, the contribution of spatial variability of rainfall reaches the peak when the rainfall intensity is within the range of 0.1–1.0 mm/h and the antecedent soil moisture is around 0.2. That is because for the saturation excess-dominant runoff process, the rainfall will convert into runoff without loss in the saturated area wherever it falls on. Due to the relatively large correlation length of the local rainfall field (60 km), the variance of rainfall increases with the subcatchment sizes. Thus the spatial variability plays a more and more important role with the increasing catchment size. However, if the catchment size exceeds the characteristic length of rainfall, the spatial variability of rainfall may be filtered as the high-frequency component.

The analysis results show that for the slow runoff response, the shape of hydrograph is largely dominated by the hillslope routing. With increasing of the runoff response velocity, the significance of the channel routing gradually raises. Besides the runoff response velocity, the catchment size is another decisive factor on the relative role of hillslope and channel. For the small catchment, both the time to peak and the dispersion of hydrograph is predominant by the hillslope routing. While for the large catchment, the average travel time in the channel has a significant growth. Therefore, the dominant role governing the shape of hydrograph is replaced by the channel routing.

The analysis in this study involves rainfall, runoff, flow routing and their interaction of their spatial pattern, which provides insight into the effect of the spatial variability in varying characteristics of rainfall and watershed. In addition, it would be useful for the estimation of the possible error of hydrologic response when the spatial distributed information is not available. Further work is required to evaluate the relative contribution of more processes (such as evapotranspiration, canopy interception, runoff partitioning) on the hydrologic response in different scales and environments, so as to guide our modeling strategy.