1 Introduction

One of the issues of optimal power flow (OPF) is the Optimal Reactive Power Dispatch (ORPD), which are the most essential tasks in the power system network operation. Within the limitations, the reduced loss of power and the stability of voltage gets sustained. Dommel and Tinney (1968) proposed a concept on optimized power system enable the optimal voltage generator combination, changing the tap in the transformers enabled taps positions, and the overall capacitors banks to be switched. In recent years, the conventional and non-conventional algorithms are the many optimization techniques are established. A conventional method which is based on mathematical programming was used to perform the OPF. Sun and Ashley (1984) and Bjelogrlic and Ristanovic (1990) proposes with the conventional Newton method such as, linear programming (LP) method that was proposed by the Alsac et al. (1990). Also Granville (1994) put forth the interior point (IP) method. Also Lu and Hsu (1995) comes along with the concept of dynamic programming and quadratic programming method that proposed by Quintana and Santos-Nieto (1989) and Varadarajan and Swarup (2008a; b, c), are used to meet the several objective function necessities the nature restrictions based type of applications. The disadvantages in the above methods consist of poor convergence, stuck at local optimum, and handling qualitative restrictions.

To control the above limitations, Zimmerman et al. (2005), Bakirtzis and Petridis (2002) and Yan et al. (2006) proposes the concept of Genetic Algorithms, followed by Mezura-Montes and Coello (2011) optimization of bio-geography (Lee and Yang 1998; Liang and Chung 2006), programming evolutionary, also followed by evolution methods that was proposed by Das and Patvardhan (2003) and Gomes and Saavedra (2002), and optimization name as Particle Swarm Optimization (PSO) proposed by Abido (2002), Yoshida and Nakanishi (2000), Zhao et al. (2005) and Vlachogiannis and Lee (2006) and differential equation evolution proposed by Varadarajan and Swarup (2008a; b, c) are the evolutionary optimization methods helped to attain the ORPD issues. An unconstrained search done by concerning evolutionary algorithms (EAs) that require the handling restrictions based additional mechanisms. The multiple optimal solutions, which is flexible and through the single run. So the multi objective optimization issues are entirely suitable. The different handling restrictions techniques have been proposed and concerned with Evolutionary Algorithms by Mezura and Coello (2003), Qu and Suganthan (2011) and Zhou and Zhang (2011) represents in literature part. The global optimum solution found in many cases (Ghorbani et al. 2020).

Differential evolution (DE) is the main important handling constrained based optimization issues, which is maximum efficient. DE has some advantages like finding nearest-optimal results not necessary of initial parameters, fast convergence and less control parameters only needed. In this paper, new variant of differential evolutionary, named SBDE is presented which was proposed by Sharma et al. (2014). Global search and local search are the important terms in optimization. To take care of the right balance between the above two search techniques, a replacement mutation operation is introduced. SBDE algorithm helps for discrete optimal dispatch of reactive power issue evaluation. The important thing of discretization process is to realize a solution quality, which is better in ORPD issues. The algorithm gets evaluated on IEEE 14-bus power systems and IEEE 30-bus power systems. The performance of the proposed SBDE algorithm gets compared to the existing methods. The organization of the paper given below: Sect. 2 depicts an ORPD issue formulation. Section 3 explains the overview of DE briefly; Sect. 4 presented the proposed SBDE algorithm for ORPD issue evaluation. Section 5 depicts the proposed SBDE algorithm performance gets examined by testing on IEEE 14-bus power systems and power system of IEEE 30- bus and the results. Section 6 illustrates the concludes the work.

2 Problem statement

The restrictions and the objective functions in the form of mathematical representation that can be represents as follow below:

$$ \min /{\text{Max f}}\left( {{\text{x}},{\text{u}}} \right) $$
(1)
$$ {\text{g}}\left( {{\text{x}},{\text{u}}} \right) = 0 $$
(2)
$$ {\text{h}}\left( {{\text{x}},{\text{u}}} \right) \le 0 $$
(3)
$$ {\text{U}}^{{{\text{min}}}} \le {\text{U}} \le {\text{U}}^{{{\text{max}}}} $$
(4)
$$ {\text{X}}^{{{\text{min}}}} \le {\text{X}} \le {\text{X}}^{{{\text{max}}}} $$
(5)

where \({\text{f}}\left( {{\text{x}},{\text{u}}} \right)\) describes the objective function, \({\text{g}}\left( {{\text{x}},{\text{u}}} \right)\) referred as the restrictions on equal, \({\text{h}}\left( {{\text{x}},{\text{u}}} \right)\) refers the restrictions on unequal vector arguments x and u. x refers the magnitude based load bus voltage, the output of generator based reactive power and the transmission flow line. u describes the control variable consisting of generator bus voltage, settings on taps of the transformer and shunt based VAR compensation.

The transmission network enabled the loss of real power, which is the abridge function. The phase angles, and the magnitude of bus voltage are the control variable functions. The representation function of power loss given below:

$$ {\text{f}} = \min {\text{P}}_{{{\text{loss}}}} = {\text{F}}_{{{\text{obj}}}} \left( {{\text{x}},{\text{u}}} \right) = \mathop \sum \limits_{{\begin{array}{*{20}c} {k \in {\text{N}}_{{\text{l}}} } \\ {k \in \left( {i,j} \right)} \\ \end{array} }} {\text{g}}_{{\text{k}}} \left( {{\text{V}}_{{\text{i}}}^{2} + {\text{V}}_{{\text{j}}}^{2} - 2{\text{V}}_{{\text{i}}} {\text{V}}_{{\text{j}}} {{\cos\theta }}_{{{\text{ij}}}} } \right). $$
(6)

In the above equation, \({\text{P}}_{{{\text{loss}}}}\) is the overall loss of real power, \({\text{N}}_{{\text{l}}}\) is the overall transmission lines, \({\text{g}}_{{\text{k}}}\) is the branch k conductance, \({\text{V}}_{{\text{i}}}\) is the ith bus voltage, \({\text{V}}_{{\text{j}}}\) is the jth bus voltage, \(\theta_{{{\text{ij}}}}\) is the difference of i and j based voltage phase.

2.1 Equality constraints

The equations of power balance for both real and reactive power described as

$$ {\text{P}}_{{\text{i}}} - {\text{V}}_{{\text{i}}} \mathop \sum \limits_{{{\text{j}} = 1}}^{{{\text{N}}_{{\text{B}}} }} {\text{V}}_{{\text{j}}} \left( {{\text{G}}_{{{\text{ij}}}} {{\cos}}\theta_{{{\text{ij}}}} + {\text{B}}_{{{\text{ij}}}} {\text{sin}}\theta_{{{\text{ij}}}} } \right) = 0\quad {\text{i}} = 1,2, \ldots {\text{N}}_{{\text{B}}} - 1 $$
(7)
$$ {\text{Q}}_{{\text{i}}} - {\text{V}}_{{\text{i}}} \mathop \sum \limits_{{{\text{j}} = 1}}^{{{\text{N}}_{{\text{B}}} }} {\text{V}}_{{\text{j}}} \left( {{\text{G}}_{{{\text{ij}}}} {\text{sin}}\theta_{{{\text{ij}}}} - {\text{B}}_{{{\text{ij}}}} {{\cos}}\theta_{{{\text{ij}}}} } \right) = 0\quad {\text{i}} = 1,2, \ldots {\text{N}}_{{{\text{PQ}}}} $$
(8)

where \({\text{P}}_{{\text{i}}}\) is the generation of real power,\({\text{Q}}_{{\text{i}}}\) is the generation of reactive power, \({\text{G}}_{{{\text{ij}}}}\) is mutual conductance, \({\text{B}}_{{{\text{ij}}}}\) is the mutual susceptance, \({\text{N}}_{{\text{B}}}\) is the total buses, \({\text{N}}_{{\text{B}}} - 1\) is the excluding slack bus over the total buses, \({\text{N}}_{{{\text{PQ}}}}\) is the total \({\text{PQ}}\) buses, respectively.

The Inequality constraints given below.

2.2 Restrictions on voltage

The restricted generator bus voltage through the low and high limits given below:

$$ {\text{V}}_{{\text{i}}}^{{{\text{min}}}} \le {\text{V}}_{{\text{i}}} \le {\text{V}}_{{\text{i}}}^{{{\text{max}}}} ;\quad {\text{i}} \in {\text{N}}_{{\text{g}}} $$
(9)

where \({\text{V}}_{{\text{i}}}^{{{\text{min}}}} {\text{ and V}}_{{\text{i}}}^{{{\text{max}}}}\) define minimum and maximum generator voltage.

2.3 Real power capability limit based generator

The restricted real power generator through the low and high limits given below:

$$ {\text{P}}_{{{\text{gi}}}}^{{{\text{min}}}} \le {\text{P}}_{{{\text{gi}}}} \le {\text{P}}_{{{\text{gi}}}}^{{{\text{max}}}} $$
(10)

where \({\text{P}}_{{{\text{gi}}}}^{{{\text{min}}}} {\text{ and P}}_{{{\text{gi}}}}^{{{\text{max}}}}\) define min and max of real power generator.

2.4 Reactive power capability limit based generator

The restricted reactive power generator through the low and high limits given below:

$$ {\text{Q}}_{{{\text{gi}}}}^{{{\text{min}}}} \le {\text{Q}}_{{{\text{gi}}}} \le {\text{Q}}_{{{\text{gi}}}}^{{{\text{max}}}} ;\quad {\text{i}} \in {\text{N}}_{{\text{g}}} $$
(11)

where \({\text{Q}}_{{{\text{gi}}}}^{{{\text{min}}}}\) and \({\text{Q}}_{{{\text{gi}}}}^{{{\text{max}}}}\) define min and max of reactive power generator, Ng is the total generator buses.

2.5 Reactive power compensation limits

The restricted compensation of shunt VAR through the low and high limits given below:

$$ {\text{Q}}_{{{\text{ci}}}}^{{{\text{min}}}} \le {\text{Q}}_{{{\text{ci}}}} \le {\text{Q}}_{{{\text{ci}}}}^{{{\text{max}}}} ;\quad {\text{i}} \in {\text{N}}_{{\text{c}}} $$
(12)

where \({\text{Q}}_{{{\text{ci}}}}^{{{\text{min}}}}\) and \({\text{Q}}_{{{\text{ci}}}}^{{{\text{max}}}}\) define minimum and maximum of ith represents the bank of the capacitor, Nc is the total bank of the capacitor.

2.6 Transformer tap ratio

The transformer tap ratio lower and upper limits can be expressed as:

$$ {\text{t}}_{{\text{k}}}^{{{\text{min}}}} \le {\text{t}}_{{\text{k}}} \le {\text{t}}_{{\text{k}}}^{{{\text{max}}}} ;\quad {\text{k}} \in {\text{N}}_{{\text{T}}} $$
(13)

where \({\text{t}}_{{\text{k}}}^{{{\text{min}}}}\) and \({\text{t}}_{{\text{k}}}^{{{\text{max}}}}\) define minimum and maximum of transformer tap setting at branch k, NT is the total transformer in the system.

2.7 Line flow limits

The apparent line flow limits are expressed as:

$$ {\text{S}}_{{\text{l}}} \le {\text{S}}_{{\text{l}}}^{{{\text{max}}}} \quad {\text{l}} \in {\text{N}}_{{\text{l}}} . $$
(14)

3 Differential evolution algorithms

The Stochastic Population-based Optimization Algorithm based DE algorithm, which is the most powerful. It was created by Storn and Price (1995). The primary thought behind DE is a scheme is for creating a new offspring. The crossover and the mutation are utilized for new offspring generation, selection decides if the objective vector or the survival of preliminary vector to the next generation. The DE exhibition is sensitive to the mutation function, crossover function, and population size.

Algorithm:

The procedure of Differential Evolution algorithm given below:

Step 1: Generation G enabled individual i, which is a multidimensional vector

$$ {\text{X}}_{{{\text{i}},{\text{k}}}}^{{\text{G}}} = { }\left( {{\text{X}}_{{{\text{i}},1}} , \ldots ,{\text{X}}_{{{\text{i}},{\text{D}}}} } \right). $$

To initialized the initial population as given below:

$$ {\text{X}}_{{{\text{i}},{\text{k}}}}^{{\text{G}}} = {\text{X}}_{{{\text{k}},{\text{min}}}} + {\text{rand}}\left( {0,1} \right) \times \left( {{\text{X}}_{{{\text{k}},{\text{max}}}} - {\text{X}}_{{{\text{k}},{\text{min}}}} } \right)\quad {\text{i}} \in \left[ {{\text{i}},{\text{N}}_{{\text{p}}} } \right],{\text{k}} \in \left[ {1.{\text{D}}} \right], $$
(15)

where Np is the total population and D is the total control variables. \({\text{X}}_{{{\text{k}},{\text{min}}}}\), \({\text{X}}_{{{\text{k}},{\text{max}}}}\) define minimum and maximum of each variable k.

Step 2: For each \({\text{i}} \in \left[ {1, \ldots ,{\text{N}}_{{\text{p}}} } \right]\) the arbitrary selected individuals \({\text{X}}_{{{\text{r}}2}}\) and \({\text{X}}_{{{\text{r}}3}}\) i.e. weighted differences, which additioned of other arbitrary selection of an individuals \({\text{X}}_{{{\text{r}}1}}\) to construct a Vi i.e. mutated vector.

Strategy 1: “DE/1/rand/1” (Classical strategy)

$$ {\text{V}}_{{\text{i}}} = {\text{X}}_{{{\text{r}}1}}^{{\text{G}}} + {\text{F}} \cdot { }\left( {{\text{X}}_{{{\text{r}}2}}^{{\text{G}}} - {\text{X}}_{{{\text{r}}3}}^{{\text{G}}} } \right). $$
(16)

Strategy 2: “DE/local-to-best/1”

$$ {\text{V}}_{{\text{i}}} = {\text{old}}_{{\text{i}}}^{{\text{G}}} + {\text{F}}.{ }\left( {{\text{best}}^{{\text{G}}} - {\text{old}}_{{\text{i}}}^{{\text{G}}} } \right){\text{F}}.{ }\left( {{\text{X}}_{{{\text{r}}2}}^{{\text{G}}} - {\text{X}}_{{{\text{r}}3}}^{{\text{G}}} } \right). $$
(17)

Strategy 3: “DE/best/1 with jitter”

$$ {\text{V}}_{{\text{i}}} = {\text{best}}^{{\text{G}}} + {\text{jitter}} + {\text{F}} \cdot \left( {{\text{X}}_{{{\text{r}}2}}^{{\text{G}}} - {\text{X}}_{{{\text{r}}3}}^{{\text{G}}} } \right). $$
(18)

The expression (18) is used, where jitter described as 0.0001 rand + F.

Strategy 4: “DE/rand/1 with per-vector-dither”

$$ {\text{V}}_{{\text{i}}} = {\text{X}}_{{{\text{r}}1}}^{{\text{G}}} + {\text{dither}} \cdot { }\left( {{\text{X}}_{{{\text{r}}2}}^{{\text{G}}} - {\text{X}}_{{{\text{r}}3}}^{{\text{G}}} } \right). $$
(19)

By concerning of this expression, where the evaluation of dither as given, \(\mathrm{dither}=\mathrm{F}+\mathrm{rand}. \left(1-\mathrm{F}\right).\)

By this concern, the DE has a much stronger.

Strategy 5: “DE/rand/1 with per-generation-dither”.

By concerning of strategy 4 described, but dither is only evaluated per-generation once.

Strategy 6: “DE/rand/1 with either-or algorithm”

$$ {\text{V}}_{{\text{i}}} = {\text{X}}_{{{\text{r}}1}}^{{\text{G}}} + {\text{K}} \cdot \left( {{\text{X}}_{{{\text{r}}2}}^{{\text{G}}} - {\text{X}}_{{{\text{r}}3}}^{{\text{G}}} - 2 \cdot {\text{X}}_{{{\text{r}}1}}^{{\text{G}}} } \right). $$
(20)

With \(\mathrm{K}=0.5. \left(\mathrm{F}+1\right).\)

In Eqs. (16)–(20), \(\mathrm{i},{\mathrm{r}}_{1},{\mathrm{r}}_{2}\mathrm{ and }{\mathrm{r}}_{3}\) are reciprocally several indices. \(\mathrm{F}\) is the step size and it gets to selected from the range between [0, 2].

Step 3: The prey vector \({\mathrm{X}}_{\mathrm{i}}\) is combined with \({\mathrm{V}}_{\mathrm{i}}\), the trial vector \({\mathrm{u}}_{\mathrm{i}}\) gets to relented represented as follows:

$$ {\text{u}}_{{\text{i}}} = {\text{u}}_{{{\text{i}},{\text{k}}}}^{{{\text{G}} + 1}} = \left\{ {\begin{array}{*{20}c} {{\text{V}}_{{{\text{i}},{\text{k}}}} } & {if\;{\text{rand}}_{{{\text{k}},{\text{i}}}} \le CR\;\;({\text{or}})\;\;k = {\text{I}}_{{{\text{rand}}}} } \\ {{\text{X}}_{{{\text{i}},{\text{k}}}}^{{\text{G}}} } & {if\;{\text{rand}}_{{{\text{k}},{\text{i}}}} > CR\;\;and\;\;k \ne {\text{I}}_{{{\text{rand}}}} .} \\ \end{array} } \right. $$
(21)

where \({\text{rand}}_{{{\text{k}},{\text{i}}}} \in \left[ {0,1} \right]\) and \({\text{I}}_{{{\text{rand}}}}\) is the random selection within the interval range of \(\left[ {1, \ldots ,{\text{D}}} \right]\). To initiates each vector from Vi. The Eq. (21) represents the each vector component \({\text{i}} \in \left[ {1, \ldots ,{\text{N}}_{{\text{p}}} } \right],\,{\text{k}} \in \left[ {1, \ldots ,{\text{D}}} \right]\). CR is the crossover operator and the wide range between as [0, 1].

Step 4: The next generation based individuals selection as follows:

$$ {\text{X}}_{{\text{i}}}^{{{\text{G}} + 1}} = \left\{ {\begin{array}{*{20}l} {{\text{u}}_{{\text{i}}}^{{{\text{G}} + 1}} } \hfill & {if f\left( {{\text{u}}_{{\text{i}}}^{{{\text{G}} + 1)}} \le f\left( {{\text{X}}_{{\text{i}}}^{{\text{G}}} } \right)} \right)} \hfill \\ {{\text{X}}_{{\text{i}}}^{{\text{G}}} } \hfill & {otherwise.} \hfill \\ \end{array} } \right. $$
(22)

Step 5: Repeat the steps i.e., mutation steps, crossover steps, and selection operator steps till the system termination happen like as the total generations get to maximum and get to met.

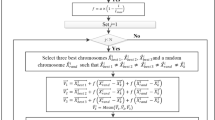
Figure 1 shows the Differential Evolution Algorithm flow diagram. Figure 2 shows the SBDE algorithm implementation for Optimal Reactive Power Dispatch (ORPD) issue.

Fig. 1
figure 1

Differential evolution algorithm flow diagram

Full size image
Fig. 2
figure 2

Flow chart of the implemented SBDE

Full size image

4 Self-balanced differential evolution (SBDE) algorithm

SBDE is a new updation of DE technique, which is proposed by Harish et al. (2014). The proper balance get to sustain between the local and global search, a new mutation operation is introduced. It is given in Eq. (23).

$$ {\text{V}}_{{\text{i}}} = {\text{C*X}}_{{{\text{r}}1}}^{{\text{G}}} + {\text{F}} \cdot \left( {{\text{X}}_{{{\text{r}}2}}^{{\text{G}}} - {\text{X}}_{{{\text{r}}3}}^{{\text{G}}} } \right) $$
(23)

where G define generation and \(\mathrm{C}\) define cognition learning factor.

The probability of fitness is calculated using Eq. (24).

$$ {\text{F}}_{{\text{i}}}^{{{\text{G}} + 1}} = \left( {{\text{rand}}\left( {0,1} \right) - 0.5} \right) \times \left( {1.5 - {\text{prob}}_{{\text{i}}}^{{\text{G}}} } \right). $$
(24)

From above equation the probability is calculated as

$$ {\text{prob}}_{{\text{i}}}^{{\text{G}}} = \frac{{0.9 \times {\text{fitness}}^{{\text{G}}} }}{{{\text{maxfit}}^{{\text{G}}} }} + 0.1 $$
(25)

C varies between [0.1–1]. It controls the balance between search strategies. Hence the scale factor range as \(\mathrm{F}\) gets varied energitically. By varying C and F, DE can be balanced easily.

4.1 Implementation of SBDE for ORPD

The implementation of SBDE is based on the retribution function method. The sum of objective functions and its retribution terms represented as given below:

$$ \begin{aligned} {\text{F}} & = {\text{f}} + {\text{R}}_{1} \left( {{\text{P}}_{{{\text{g}}1}} - {\text{P}}_{{{\text{g}}1}}^{{{\text{lim}}}} } \right)^{2} + \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{N}}_{{{\text{PQ}}}} }} {\text{R}}_{2} \left( {{\text{V}}_{{\text{i}}} - {\text{V}}_{{\text{i}}}^{{{\text{lim}}}} } \right)^{2} \\ & \quad + \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{N}}_{{\text{g}}} }} {\text{R}}_{3} \left( {{\text{Q}}_{{{\text{gi}}}} - {\text{Q}}_{{{\text{gi}}}}^{{{\text{lim}}}} } \right)^{2} + \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{N}}_{{\text{l}}} }} {\text{R}}_{4} \left( {\left| {{\text{S}}_{{\text{l}}} - {\text{S}}_{l}^{{{\text{max}}}} } \right|} \right)^{2} . \\ \end{aligned} $$
(26)

The associated retribution coefficient such as \({\mathrm{R}}_{1}\),\({\mathrm{R}}_{2}\),\({\mathrm{R}}_{3}\), \({\mathrm{R}}_{4}\) with the generation of real power, magnitude of bus voltage, generation of reactive power and the limit violation of apparent line flow independently.

5 Numerical results and discussions

Under several cases, to examine the proposed algorithm ability, the bus system namely as IEEE 14 and IEEE 30 gets review. Each test systems with the optimum solution to examine the proposed algorithms, 50 individual trials. The proposed algorithms implementation in MATLAB Platform and the simulation conducted on a personal computer “2.30 GHz of Turbo Boost up system, Core i5-2410M Processor with the range of 2.90 GHz—4 GB RAM”. The flow power considered concerning the MATPOWER 6.0 software (Zimmerman et al. 2005). Table 1 shows the minimization parameter settings for the proposed algorithms for different system.

Table 1 Minimization parameter settings
Full size table

5.1 Bus power system: IEEE 14

There are 20 branches in the IEEE 14-bus, which consist of five generators at 1, 2, 3, 6 and 8 buses system, three transformer tap settings at 4–7, 4–9 and 5–6 and two capacitors are placed at bus 9 and bus 14. The system data was taken from Palappan and Thangavelu (2018), Amrane et al. (2015) and Ghasemi and Ghavidel (2014) followed by Anuradha et al. (2020). The boundary condition for control variables like the generator voltage magnitude is 0.95–1.1, transformer taps is 0.95–1.1 and shunt VARs are 0–0.3.

The system total generation, load and power loss are as follows:

$$ \sum {\text{P}}_{{\text{G}}} = 272.55{\text{ MW}},{ }\sum {\text{Q}}_{{\text{G}}} = 104.54{\text{ MVAr}}, $$
(27)
$$ {\text{P}}_{{{\text{load}}}} = 259.00{\text{ MW}},{\text{ Q}}_{{{\text{load}}}} = 73.50{\text{ MVAr}}, $$
(28)
$$ {\text{P}}_{{{\text{loss}}}} = 13.393{\text{ MW}}. $$
(29)

The proposed SBDE algorithm, DE strategy, Genetic Algorithm (GA) and some existing algorithm gets to compared and provides the ORPD issue enabled control variables of optimal solution gets attained were described in Table 2a, b. From the Table 2a, b shows all the control factors attained within the well founded protected limitations. By consider the proposed algorithms, Table 3 illustrates overall comparison through the following separation of real power loss such as Minimum, Average, Maximum, Standard Deviation and Average Consumption Time. Above table shows the reduction of real power loss for the SBDE algorithm, DE-strategy techniques and GA of the proposed algorithms and existing methods such as 27.0731%, 27.0626%, 27.0477%, 27.0604%, 27.0462%, 23.8393%, and 27.0276% and 22.9702% respectively. Besides, the computational time is illustrated as 3.5436 s, 3.5589 s, 3.5590 s, 3.5589 s, 3.5590 s, 3.9478 s, 3.5592 s, where the computational times of GA and DFA proposed by Palappan and Thangavelu (2018) is 3.9557 s and 4.0914 s, independently. The performance of the loss reduction as minimum, which is greater with SBDE, DE-strategy 3, 5 and 6. Similarly, SBDE provides the computational time as lesser. The performance characteristics of real power loss by several methods like existing and proposed method illustrates in Figs. 3 and 4. From the simulation results the SBDE gives the better optimal solution compared to all other algorithms.

Table 2 The test system of IEEE 14-bus to the losses of real power and best control variables
Full size table
Table 3 The test power system of IEEE 14 bus based statistical details
Full size table
Fig. 3
figure 3

Performance characteristics of real power loss for IEEE-14 bus system using SBDE-DE 3

Full size image
Fig. 4
figure 4

Performance characteristics of real power loss for IEEE-14 bus system using DE

Full size image

5.2 Bus power system: IEEE 30

IEEE 30-bus system is the second test system there are 41 branches which six generators 1, 2, 5, 8, 11 and 13 at buses. 6–9, 6- 10, 4–12, and 27–28 are the four transformer tap settings. For case 1, to placed the bus 10 and 24 are the two capacitors banks as given in Amrane et al. (2015). In case 2, three capacitor banks were placed at bus 3, 10 and 24 as given in Ghasemi and Ghavidel (2014). The new emplacement of capacitor banks done in case 3, which generated at buses 10, 12, 15, 17, 20, 21, 23, 24 and 29 represented in Sahli and Hamouda (2018). The boundary condition for control variables like the generator voltage magnitude is 0.95–1.1, transformer taps is 0.95–1.1. For case 1 and case 2 the shunt VARs limits is 0–0.3, and for case 3 0–0.05.

The system total generation, load and power loss are as follows:

$$ \sum {\text{P}}_{{\text{G}}} = 290.71\;\;{\text{MW}},\;\;\sum {\text{Q}}_{{\text{G}}} = 122.49\;\;{\text{MVAr}}, $$
(30)
$$ {\text{P}}_{{{\text{load}}}} = 283.40\;\;{\text{MW}},\;\;{\text{Q}}_{{{\text{load}}}} = 126.20\;\;{\text{MVAr}}, $$
(31)
$$ {\text{P}}_{{{\text{loss}}}} = 7.307\;\;{\text{MW}}. $$
(32)

Case 1: The bus test system of IEEE-30 with restrictions used in Sahli and Hamouda (2018), Ghasemi and Ghavidel (2014) and Jeyadevi and Baskar (2011), (12 control variables).

Case 2: The bus test system of IEEE-30 with restrictions used in Ghasemi and Ghavidel (2014) and Sulaiman and Mustaffa (2015) (13 control variables).

Case 3: The bus test system of IEEE-30 with restrictions used in Abaci and Yamacli (2016), Davoodi and Babaei (2019), Villa-Acevedo and Lopez-Lezama (2018) and Medani and Sayah (2017) (19 control variables).

ORPD issue based control variables attained by SBDE, DE-strategy (1–6) and GA algorithm and the several existing algorithms shown in Tables 4a, b, 5a, b, 6a, b. By consider the table, the proposed system seemed as better and all the control factors achieved within the corresponding protected limits. Table 6a, b shows the best optimal solutions calculation through the different systems of 50 runs for the test systems of IEEE 30-bus for three different cases. From the table, the loss of real power for the proposed SBDE performance for three different cases is 0.04905, 0.04571 and 0.042946 p.u, independently. The SBDE algorithm, DE-strategy (1–6) and GA performance for different cases for IEEE 30-bus system in Figs. 5, 6, 7, 8, 9 and 10. From the simulation results the SBDE gives the optimal solution compared to all other algorithms. Table 7 illustrates the overall comparison i.e. the loss of real power, standard deviation and average computation time represented as follows: minimum, average, maximum for proposed algorithms, SBDE, DE strategy (1–6) and the current performance shown in the literature section. From the performance analysis, we can represent that the SBDE gives the better optimal solution matched to the existing DE-strategies technique and GA. At the initial search phase, the control variables have an initial fluctuation, and next settled down at the final search phase to a steady state. The nearest optimal solution achieved by the SBDE algorithm, which gives the best characteristic performance, which is effectiveness and robustness to the other existing algorithms.

Table 4 For case 1, the bus test system of IEEE 30 enabled best control variables
Full size table
Table 5 For case 2, the bus test system of IEEE 30 enabled best control variables
Full size table
Table 6 For case 3, the bus test system of IEEE 30 enabled best control variables
Full size table
Fig. 5
figure 5

Real power loss analysis for IEEE-30 bus system using SBDE-DE3 (Case 1)

Full size image
Fig. 6
figure 6

Real power loss analysis for IEEE-30 bus system using DE 4-GA (Case 1)

Full size image
Fig. 7
figure 7

Real power loss analysis for IEEE-30 bus system using SBDE-DE 3 (Case 2)

Full size image
Fig. 8
figure 8

Real power loss analysis for IEEE-30 bus system using DE 4-GA (Case 2)

Full size image
Fig. 9
figure 9

IEEE-30 bus system voltage profile

Full size image
Fig. 10
figure 10

Real power loss analysis for IEEE-30 bus system using DE 4-GA (Case 3)

Full size image
Table 7 Statistical details for IEEE 30–bus test power system
Full size table

6 Conclusion

The proposed self-balanced differential evolution (SBDE) algorithm, DE-approach (1–6) and GA approaches for ORPD issue evaluation. SBDE algorithm helps to manipulate the mutation and crossover are flexible on the existing suitable value. SBDE algorithm enabled the bus test system like as IEEE 14 and IEEE 30. The performance analysis compared to the DE-strategy, GA and other methods addressed in the reference. From the SBDE algorithm illustrates the losses of real power were minimized more than any other techniques. In addition the computation time is also very less. This demonstrates that the system is progressively powerful in worldwide looking through capacity and computational effectiveness. The investigations of the outcomes are extremely encouraging the proposed system gets accomplished. The minimum loss of real power attained in the state and control variables were carried to its corresponding boundary condition.