Visualizing particle velocity from dual-camera mixed reality video images using 3D particle tracking velocimetry

Abstract

Mixed reality (MR) systems integrate diverse sensors, allowing users to visualize and interact with their surroundings. Mixed reality headsets typically include synchronized front-facing cameras that, among other things, can be used to track tracer particles (such as snowflakes) to estimate particle velocity field in real time. The current work presents a 3D particle tracking velocimetry method for use with MR devices, which combines binocular disparity and various monocular cues to estimate particle distance from an observer. This distance information is then incorporated into a particle tracking velocimetry algorithm to generate a three-dimensional visualization of the particle velocities. The resulting mixed reality particle tracking velocimetry (MR-PTV) approach was initially tested using synthetic particle data obtained by discrete element method simulations, resulting in a detailed error assessment of the method. The approach was then experimentally validated for particles transported in a wind tunnel and in a water flume flow using the Microsoft HoloLens 2 MR headset to image the particle motion. The resulting MR-PTV system can be used for mixed reality particle velocity visualization in a variety of industrial, scientific, and recreational purposes.

Graphical abstract

1 Introduction

Particle Tracking Velocimetry (PTV) is a well-known method to compute the velocity field of a set of particles by tracking the particle positions through a series of time steps. The 2D PTV technique is standard in fluids laboratory environments, where a laser sheet is typically used to illuminate particles passing through a planar transect of the flow, thereby providing the distance between the imaging camera and the illuminated particles (Adrian and Westerweel 2011). A wide variety of different 3D PTV/PIV methods have also been proposed for different applications (Arroyo and Hinsch 2008). For microfluidics problems, the defocusing (or astigmatic) PTV/PIV approach is widely used (Barnkob et al. 2015, 2021; Lin et al. 2008; Liu et al. 2014; Pereira and Gharib 2002). Particle images in defocusing PTV appear as varying shapes or have a change in radial blur in correlation to the particle depth, so the method requires particles to be highly spherical and of uniform size. Holographic PIV (HPIV) uses double-exposed holograms of a field of seed particles using two reference waves (Bryanston-Cross et al. 1992; Hinsch 2002; Pu et al. 2000; Owen and Zozulya 2000; Murata and Yasuda 2000). However, the HPIV method has suffered from low signal-to-noise ratio, limitations to small measurement volumes, and equipment requirements to make holograms not suited for use in field applications. Tomographic PTV/PIV uses an illuminated volume and multiple cameras (typically four or more) aligned in various configurations to reconstruct particle images in a voxel space and track 3D particle motions through time in different sections of the flow field (Scarano 2013; Elsinga et al. 2006). The tomographic PTV/PIV method can give precise results in laboratory situations, but it uses a camera configuration that is not achievable with a headset. Shake-The-Box PTV (Schanz et al. 2016) takes known particle positions from previous time steps to initialize the particle distribution at future time steps followed by a “shaking” alignment process which adjusts the predicted particle position to the actual particle position. New approaches in Lagrangian particle tracking technology have made tremendous progress in recent years (Schröder and Schanz 2023); however, systems require precise camera calibration procedures (Bruecker et al. 2020) and fixed camera apparatuses, making it challenging for use in mobile field applications.

Advances in wearable mixed reality headsets have opened a new avenue for PTV/PIV applications. Cierpka et al. (2021) created a smartphone app with sufficient PIV capabilities, which is suitable for students in a laboratory setting that may not typically have access to advanced PIV systems. There is also opportunity to integrate mobile real-time PTV with wearable technology, such as mixed reality headsets, to be used as a tool for flow visualization and approximate velocity measurement for seed particles (natural or man-made) carried by flow. Mixed reality (MR) devices capable of even rough velocity measurements have potential for industrial and other applications, such as targeting or for estimating dispersal of obscurant clouds or released chemicals. Such MR devices could also be used for visualizing flow about structures (e.g., buildings) or environmental flows generated by thermal or salinity gradients. Advanced MR devices have an inertial measurement unit and two or more synchronized visible light cameras, attached to a small computer. In some MR operations, seed particles would be naturally occurring (such as snowflakes) and flow visualization of particles must be performed with ambient lighting at the frame rate of the video camera. For such systems, the question is, how can we utilize ambient conditions to enhance a particle tracking algorithm?

Relevant to addressing this question, we outline how visual monocular cues (observed with a single eye) can be used to match similar particles in stereo images. Monocular cues include a wide range of observations that often depend on the type of image under consideration. Examples of common monocular cues include relative size and brightness of similar objects, apparent convergence of parallel lines (e.g., railroad tracks), motion parallax (Mizushina et al. 2020), relative degree of blur between objects in field of view (Held et al. 2010), and texture variations (Saxena et al. 2007). Several papers have demonstrated improved depth estimation using various approaches for combining binocular disparity with different monocular cues (Kellnhofer et al. 2016; Kowdle et al. 2012; Saxena et al. 2007); however, this work has dealt with images having a continuous gradation of intensity and textures. By contrast, PTV/PIV images appear as a cloud of dots, each with different distances from the cameras and appearing in the images with different sizes and velocities. Bao and Li (2011) showed that correct particle matching, between left and right stereo images, was significantly improved when using radial blur as an additional constraint to epipolar geometry. In the current paper, we take this idea a step further by using a variety of monocular cues, such as particle image size, intensity, velocity and projected position in novel matching and linking PTV algorithms optimized for ambient conditions.

The current paper presents novel algorithms to combine monocular and binocular cues to enhance particle linking and matching functions in a series of PTV images, consisting of a field of particles and obtained using a dual-camera MR device. Depth estimates are used to reconstruct 3D particle locations, which can be tracked through time to compute particle velocities. The resulting algorithm, referred to as Mixed Reality Particle Tracking Velocimetry (MR-PTV), is shown in Sect. 2. Section 2 also provides a detailed error analysis of the proposed method for particle depth estimation. In Sect. 3, MR-PTV performance is assessed using synthetic particle motion images, both for uniform flow and for homogeneous isotropic turbulence. In Sect. 4, MR-PTV performance is validated experimentally both in hydraulic flume experiments and for particulate flow in a wind tunnel. Conclusions are shown in Sect. 5.

2 Methodology

This section presents a methodology for combining monocular and binocular cues for performing volumetric 3D PTV with a two-camera MR device. It is assumed that both cameras of the MR device are co-directional (front-facing), take synchronized grayscale images at a fixed frame rate, are separated by a baseline distance h in the x-direction of a global Cartesian coordinate system, and have focal length f. The field of view of each camera substantially overlaps that of the other camera, with equal focal lengths for both cameras. The origin of the global Cartesian coordinates is located at the point half-way between the cameras, and the z-direction is taken as the distance away from the cameras in the direction of sight (Fig. 1). Image plane coordinates ($X^{L} ,Y^{L}$) and ($X^{R} ,Y^{R}$) are assigned to the left and right camera, respectively. The origin of each image plane coordinate system is the center of the respective image plane. We use upper-case letters to denote variables in the image plane and lower-case letters to denote variables in the global coordinate system throughout the paper.

Fig. 1

Sketch showing the left (L) and right (R) cameras and the associated global coordinate system (x, y, z), where the image plane is indicated by a red line, with left camera image plane coordinates ($X^{L} ,Y^{L}$) and right camera image plane coordinates ($X^{R} ,Y^{R}$)

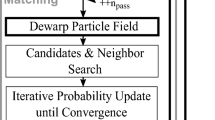
Figure 2 provides a block diagram showing the series of steps required to track particles in 3D space using the two-camera MR device. The first step, on the far left of Fig. 2, is image acquisition by the two cameras. MR devices typically do not offer adjustable image acquisition rates (as is typical for cross-correlation cameras used for PIV and PTV), limiting the velocity of particle motion that can be acquired with the system. The output of the image acquisition step is two synchronized video feeds, one from each stereo camera. Each video frame is taken at a constant time step, then processed using the MR-PTV algorithm shown in Fig. 2. The first step of the MR-PTV algorithm involves particle detection in images by using a local adaptive binarization technique (Sauvola and Pietikäinen 2000). The output from the particle detection step includes measurement of image plane variables such as centroid position ($X^{L} ,Y^{L}$), diameter $D^{L}$, and brightness $B^{L}$ for each particle seen in the image plane of the left camera, with these measurements repeated for the right camera. The particle linking step employs a dynamic linking algorithm, enhanced by monocular features, to link particles between successive frames. The particle matching step matches particles between left and right camera images. The matching algorithm, again, makes use of monocular cues, along with epipolar geometry constraints to match a particle between left and right stereo images. A binocular disparity algorithm is then used to estimate the distance of each particle from the origin. The previous steps result in a series of global position estimates for each particle over a series of frames. To reduce noise in 3D velocity estimates, we utilize a moving least squares method to fit a polynomial to multiple points, which can be differentiated resulting in smoother velocity measurements throughout time.

Fig. 2

Block diagram of the MR-PTV velocity calculation algorithm

2.1 Particle linking algorithm

Since the PTV method estimates velocity based on particle displacement in time, it is necessary to track particles between consecutive video frames, a technique we refer to as "particle linking". Traditional planar 2D PTV systems link particles between frames by a nearest neighbor search method (Crocker and Grier 1996), where a search radius is specified that should be larger than the largest displacement of a particle between frames but smaller than the separation between two neighboring particles in an image. When particles move at a larger displacement between frames than the scale of separation, it can be very difficult to link particles between frames. Two ways to handle this problem are by increasing the framerate of the camera so that particles are displaced a smaller amount between frames and by decreasing the tracer particle density so particles are more dispersed throughout the image. The MR-PTV system is designed to work with stereo cameras at a fixed framerate using seed particles whose density cannot be controlled. We take advantage of the fact that in 3D PTV systems, the particles in the image plane appear to have differences in their size and brightness, even when the physical particle size and field illumination are constant. These differences are examples of “monocular cues” for particle depth, which are used to distinguish particles between frames.

The monocular cues used for particle linking include the apparent particle diameter $D_{n}$ and particle brightness $B_{n}$ measured in the image plane. In general, velocity cannot be used as a monocular cue for the linking step because velocity cannot be calculated until after a particle has been linked between consecutive frames. We implement a predictive linking algorithm to account for effects of particle motion by developing an estimate {$\tilde{X}(t_{n + 1} )$,$\tilde{Y}(t_{n + 1} )$} for the particle position in the image plane at time $t_{n + 1}$ based on the positions at the previous two time steps as

$$\tilde{X}(t_{n + 1} ) = 2X(t_{n} ) - X(t_{n - 1} ), \quad\tilde{Y}(t_{n + 1} ) = 2Y(t_{n} ) - Y(t_{n - 1} ),$$

(1)

where $\{ X(t_{n} ),Y(t_{n} )\}$ denotes the particle position in the image plane at the current time $t_{n}$. Rather than simply linking to the particle that lies nearest to the estimated position, we evaluate the group of particles near to the estimated position using a set of monocular cues. The process used for linking is shown in Fig. 3 for a sample particle denoted by ‘c’. We desire to link particle c, in the current frame at time $t_{n}$, to a particle in the successive frame at time $t_{n + 1}$. The first step after determining the estimated particle position from (1) is to identify a set of candidate target particles for linking using a hard-pass filter based on the location of particles in the image. The hard-pass filter is shown in the figure by a box of side length 2H, shown placed around the current position of particle c at time $t_{n}$ in Fig. 3a and then moved to be around the estimated position of particle c in Fig. 3c. A subset Q_b of particles in the successive frame at time $t_{n + 1}$ are considered as possible matches if the particles pass the spatial hard filter condition, given by

$$x_{n}^{L} - K < x_{m}^{R} < x_{n}^{L}, \quad\left| {\tilde{X}(t_{n + 1}^{{}} ) - X_{b}^{{}} (t_{n + 1} )} \right| \le H, \quad\left| {\tilde{Y}(t_{n + 1}^{{}} ) - Y_{b}^{{}} (t_{n + 1} )} \right| \le H,$$

(2)

where $\{ X_{b} (t_{n + 1} ),Y_{b} (t_{n + 1} )\}$ denotes the position at time $t_{n + 1}$ of a candidate particle b. It is ideal to set H large enough so that all particle links can be captured, but small enough so that relatively small subsets Q_b are considered in order to decrease computational time. A linked particle is selected as the particle from subset Q_b that minimizes the linking function G_bc, defined by

$$G_{bc} = \ell_{1} \left( {\frac{{D_{b}^{L} - D_{c}^{L} }}{{D_{ave} }}} \right)^{2} + \ell_{2} \left( {\frac{{B_{b}^{L} - B_{c}^{L} }}{{B_{ave} }}} \right)^{2} + \ell_{3} \left( {\frac{{X_{b}^{L} - \tilde{X}_{c}^{L} }}{{X_{image} }}} \right)^{2} + \left( {\frac{{Y_{b}^{L} - \tilde{Y}_{c}^{L} }}{{Y_{image} }}} \right)^{2}.$$

(3)

Fig. 3

A sequence of images illustrating the particle linking algorithm: a A field of particles in the image plane of either the left or right camera at time $t_{n}$. The hard filter region surrounding a particle c is indicated by a red box. b A close-up of the particles in the hard filter region surrounding particle c at $t_{n}$. c Four particles in the hard filter box surrounding the estimated position ($\tilde{X}_{c} ,\tilde{Y}_{c}$) of particle c at time $t_{n + 1}$, which together constitute a set Q_b. Particle c is found to link to particle 4 from this set, which minimizes the particle linking function G_bc

The particle linking procedure is performed for each camera, although the linking function is shown in (3) for the left camera. The linking function G_bc incorporates the monocular cues of apparent diameter and brightness in the image plane, and it is defined for a given camera (denoted by the left camera L in (3)) as a function of the estimated position ($\tilde{X}_{c}^{L} ,\tilde{Y}_{c}^{L}$) of particle c from (2) and the measured position ($X_{b}^{L} ,Y_{b}^{L}$) of a particle b from the set Q_b at time $t_{n + 1}$. The coefficients $\ell_{1}$, $\ell_{2}$, and $\ell_{3}$ are prescribed weights whose values are selected to try to make each term in (3) of approximately equal magnitude. The normalizing factors $D_{ave}$ and $B_{ave}$ are defined as the mean diameter and brightness in the image plane for all particles in the image. The normalizing factors $X_{image}$ and $Y_{image}$ are defined as half the image width and height as measured in the image plane, respectively. The optimal link for particle c is selected as the particle in the set Q_b that minimizes G_bc.

2.2 Stereo matching algorithm

Matching particles at each timestep, between two stereo cameras, is necessary to triangulate the depth of each particle, a procedure referred to as ‘stereo matching’. The proposed stereo matching algorithm describes how particles are matched between stereo image pairs at each time step. For a particle n at location ($X_{n}^{L} ,Y_{n}^{L}$) in the image plane of the left camera, we seek to obtain the optimal matching particle m at position ($X_{m}^{R} ,Y_{m}^{R}$) from the image plane of the right camera. A two-pronged approach rapidly identifies the matching particle. First, we employ a hard filter to limit consideration of the candidate particle set for matching of particle n, from the left camera, to only those particles m, from the right camera, for which

$$X_{n}^{L} - K{\text{ < }}X_{m}^{R} {\text{ < }}X_{n}^{L} ,\quad|Y_{n}^{L} - Y_{m}^{R} | \le S,$$

(4)

where S denotes the half-height in the y-direction. The first of these equations requires the particle position along the X-axis of the image plane of the left camera to be greater than the image in the right camera of a candidate particle match, but less than some width K, as shown in Fig. 4. For the current computations, we set K equal to 0.25 times the image width. The second equation in (4) results from the requirement that a matching particle pair should have the same Y-coordinate value based on the epipolar geometry of a co-directional camera configuration, within some range of uncertainty resulting from centroid-finding or time synchronization imperfections. In the current computations, we set S equal to 0.01 times the image height to accommodate a small margin of error. We denote by $\hat{Q}_{n}$ the set of particles from the right camera that satisfy the hard filter (4) for a given particle n in the left camera image plane. If no particle is found satisfying the hard filter (4), the particle n is identified as having no match and eliminated from further consideration.

Fig. 4

Illustration of the stereo matching algorithm, showing a pair of stereo images from the left and right cameras. In the left image, we identify a particle n and a hard filter search region, indicated by a red box. Particles a_m, b_m, and c_m in the lower right-hand image that fall in the hard filter region constitute a subset $\hat{Q}_{n}$, from which the stereo match of n is identified as particle c_m, which minimizes the function $F_{mn}$ defined in Eq. (5)

In much the same way that monocular cues were used in Sect. 2.1 to improve the particle linking algorithm, we employ various monocular cues to determine the optimal selection from the set $\hat{Q}_{n}$ of right camera particles satisfying the hard filter (4). The monocular cues make use of the fact that particles closer to the cameras appear to move faster and be both larger and brighter than particles that are farther from the cameras, even if the particles have the same velocities, diameters and brightness in physical space. The diameter, brightness and velocity differences introduced by distance can be used to distinguish between potential particle matches, since these distance-related effects should appear approximately the same when viewed by either camera. Specifically, we define a matching function $F_{nm}$ for a particle n in the left camera image plane and a candidate particle m in the right particle image plane by

$$F_{nm} = c_{1} \left( {\frac{{D_{n}^{L} - D_{m}^{R} }}{{D_{ave} }}} \right)^{2} + c_{2} \left( {\frac{{U_{n}^{L} - U_{m}^{R} }}{{U_{ave} }}} \right)^{2} + c_{3} \left( {\frac{{B_{n}^{L} - B_{m}^{R} }}{{B_{ave} }}} \right)^{2} + \left( {\frac{{Y_{n}^{L} - Y_{m}^{R} }}{{Y_{image} }}} \right)^{2}.$$

(5)

The velocity U is the apparent velocity magnitude of a particle, measured as the distance a particle moves in the image frame between consecutive frames, divided by the time interval between frames. The X-position is not considered when performing particle stereo matching because a difference in X-position in the image planes of the two cameras is expected to occur as a function of the particle distance from the cameras. Here, $c_{1}$, $c_{2}$ and $c_{3}$ are prescribed weighting coefficients, which are set so that each term in (5) has equal order of magnitude. The normalizing factors $B_{ave}$, $D_{ave}$, and $U_{ave}$ are the mean values of particle brightness, diameter and velocity magnitude in the image plane for all particles in a set of stereo images. The optimal particle match m from the right camera image plane is selected as the particle from the set $\hat{Q}_{n}$ that minimizes $F_{nm}$.

2.3 Distance estimate with binocular disparity

Binocular disparity is used to estimate particle depth in the 3D field. We consider a point P with position ($x_{n} ,y_{n} ,z_{n}$) in the global coordinate system, and position ($X_{n}^{L} ,Y_{n}^{L}$) in the image plane of the left camera and ($X_{m}^{R} ,Y_{m}^{R}$) in the image plane of the right camera, where m is the index of the matching particle from the right camera, to the particle with index n, from the left camera. The depth $z_{n}$ of the particle is the same for both cameras. We seek to back out the particle’s global coordinates based only on the coordinates measured in the two image planes. As shown in Fig. 5, triangle APa, is formed from center, A, of the left camera lens, the center, a, of the right camera lens, and the point P. Triangle, CPc, is formed from the particle apparent position, C, in the left camera image plane, to the particle apparent position, c, in the right camera image plane, and the particle position, P. Since these two triangles are similar, the ratio of base to height is equal, or

$$\frac{h}{{z_{n} }} = \frac{{h + X_{m}^{R} - X_{n}^{L} }}{{z_{n} - f}}.$$

(6)

Fig. 5

Definition of three sets of similar triangles – APa and CPc, ABC and ADP, and acb and aPd – used in distance estimation based on binocular disparity

Solving this equation for $z_{n}$ gives the particle distance from the origin in the global coordinate system as

$$z_{n} = \frac{f\,h}{{X_{n}^{L} - X_{m}^{R} }}.$$

(7)

To calculate the global coordinates, x_n and y_n for particle n, we note two similar triangles from the left camera shown in Fig. 5 by ABC and ADP, as well as two similar triangles from the right camera shown in Fig. 5 by acb and aPd. These similar triangles can be used to solve for the global particle positions in the x- and y-directions as

$$x_{n} = - h/2 + z_{n} X_{n}^{L} /f = h/2 + z_{n} X_{m}^{R} /f, \quad\,y_{n} = z_{n} Y_{n}^{L} /f = z_{n} Y_{m}^{R} /f.$$

(8)

Because we have measurements from each camera for the global coordinates x_n and y_n of each particle, we average the two measurements to reduce uncertainty, giving the global particle positions as

$$x_{n} = \frac{{z_{n} (X_{n}^{L} + X_{m}^{R} )}}{2f}, \quad{y_{n}} = \frac{{z_{n} (Y_{n}^{L} + Y_{m}^{R} )}}{2f}.$$

(9)

A test of the effectiveness of the combined stereo matching and binocular disparity algorithms for estimating particle depth was performed using 100 particles randomly distributed in a cubic computational domain with side length L. All length scales in the global coordinate system are non-dimensionalized by L in the remainder of the paper. The test was performed with particles of physical diameter d = 0.015 and baseline distance h = 0.02, using 480 × 640 pixel resolution. Figure 6 shows a plot of the estimated particle depth from the origin obtained using the MR-PTV algorithm versus the known computational depth, where each scatter point indicates the depth measurement of a particle in the field of view of both cameras. We observe that the MR-PTV estimates are grouped around the exact value, indicated by a dashed red line, and scatter points spread further from the known depth as depth increases. To understand the contribution of each of the terms in the Eq. (5) for the stereo matching function to the depth estimate, the depth estimate was repeated using only one term in the matching function, and the results of these trials are shown in Fig. 7. All the test cases that use only one term in (5) result in some points that are far from the exact values, reinforcing the need to include a variety of distance measures for accurate stereo matching.

Fig. 6

Plot of the predicted particle depth z obtained using the MR-PTV algorithm versus the known particle depth. Each particle is represented by a black circle, and an exact match is indicated by the red line. The MR-PTV predictions were obtained with coefficient values ($c_{1} ,c_{2} ,c_{3}$) = (0.100, 0.036, and 0.018), set so that each term in the matching function in Eq. (5) has approximately equal weight

Fig. 7

Effectiveness of each term in the stereo matching function given in Eq. (5). After application of the hard filter given in Eq. (4), the images in the figure compare the particle depth predicted by the MR-PTV algorithm with the known depth for cases using a only the particle brightness term, b only the particle diameter term, c only the particle velocity term, and d only the particle height Y term. The red dashed line represents an exact match between the predicted and known depth

A second series of tests was conducted to examine how the overall root-mean-square error in prediction of the particle position in the global coordinate system varies with different variables in the computation. In general, the position prediction error is a function of variables characterizing the particles, such as particle diameter d, depth of the measurement value L, and particle concentration c, as well as variables describing the camera system, such as baseline distance h, pixel width $\Delta X_{pixel}$, focal length f and field of view FOV. In Fig. 8, the dimensionless root-mean-square error in the predicted x, y and z particle positions is plotted against key combinations of these variables to characterize three specific sources of uncertainty in the MR-PTV predictions. In these results, the uncertainty associated with predicting the x- and y-positions is very similar, and significantly smaller, than the uncertainty associated with the z-position prediction. One key source of error in the MR-PTV algorithm results from resolution limitations of the particle diameter by the pixel image. This error can be characterized by plotting the root-mean-square position error as a function of the ratio $D_{image} /\Delta X_{pixel}$, where the image diameter $D_{image}$ is defined as the apparent diameter in the image plane of a particle placed at the centroid of the computational domain. The ratio $D_{image} /\Delta X_{pixel}$ is a measure of the number of pixels spanning the characteristic particle diameter in the image plane. Figure 8a was generated using ten different frames each holding 100 particles with diameter d = 0.015. The data was generated by gradually increasing the pixel resolution from 180 × 240 to 1080 × 1440 , while keeping the other variables fixed. The value of root-mean-square error in Fig. 8a increases sharply when the ratio $D_{image} /\Delta X_{pixel}$ is less than about 10.

Fig. 8

Root-mean-square error divided by the computational domain size L for the estimated positions in the x-direction (red circles), y-direction (green deltas), and z-direction (blue squares). Plots are shown comparing root-mean-square error with a number of pixels across the particle standard image-diameter $D_{image}$, b ratio of camera baseline distance h to the domain size L, and c particle area concentration in the image plane $c_{image}$

A second resolution limitation is associated with the ratio of camera baseline distance h to the measurement volume depth L. In Fig. 8b we show results from a series of tests with progressively increasing baseline distance, showing that the root-mean-square error decreases as the baseline distance to measurement volume depth ratio increases. The root-mean-square error in Fig. 8b increases rapidly for value of $h/L$ less than about 0.02. A third source of error occurs when the particle concentration becomes so high that a large amount of overlap occurs between the particles in the image plane. Overlap error can be expressed as a function of the image plane concentration c_image, defined as the ratio of the area covered by particles on the image plane to the total image plane area. A plot of the root-mean-square position error as a function of the image plane concentration is shown in Fig. 8c, where the image concentration was varied by gradually increasing the number of particles in the computation. We observe in Fig. 8c gradual increase in the root-mean-square position error with a corresponding increase in the image plane concentration.

2.4 Moving least squares differentiation

Centroid location errors and pixel resolution limitations introduce noise in estimated first order velocity measurements. To improve the 3D velocity estimate, we utilize the moving least squares method for time differentiation using a curve fit to the acquired position estimates. The moving least square method (Ghazi and Marshall 2014, Levin 1998) is used to obtain accurate derivatives of noisy measured data, denoted by $C_{m}$, $m = 1,N$. The basic idea of this method is to use a set of points in the vicinity of point $t_{n}$ , where the derivative is desired, to obtain a low-order polynomial fit $q_{n} (t)$ of the measured values $C_{m}$ on a set of points surrounding $t_{n}$; we then estimate the function derivative at $t_{n}$ by differentiating $q_{n} (t)$. For instance, selecting a quadratic polynomial as a low-order fitting function, we can write

$$q_{n} (t) = a_{n} + b_{n} (t - t_{n} ) + c_{n} (t - t_{n} )^{2},$$

(10)

where $a_{n} ,b_{n} ,c_{n}$ are undetermined coefficients. This quadratic function is fit to a set of $M$ data points on each side of the point n at which the derivative is desired by minimizing a least-square error of the form

$$E_{n} = \sum\limits_{i = n - M}^{n + M} {} [C_{i} - q_{n} (t_{i} )]^{2},$$

(11)

which yields the coefficients $a_{n} ,b_{n} ,c_{n}$. The time derivative can be estimated at $t_{n}$ using

$$\frac{dC}{{dt}}(t_{n} ) = b_{n}.$$

(12)

If $M = 1$, the moving least square procedure is equivalent to the centered difference scheme for numerical differentiation. Setting $M > 1$ serves to smooth out data fluctuations. Figure 9 demonstrates the effect of selection of M on accuracy of the derivative for the x-component of velocity predicted using the MR-PTV algorithm. Figure 9 compares the predicted velocity of a single neutrally-buoyant particle in a uniform flow for cases with M = 1, 2 and 5 particles on each side of the target particle in the moving-least-square procedure. Use of moving-least-square differentiation is shown to considerably smooth out fluctuations in the velocity calculation, yielding results close to the exact velocity value.

Fig. 9

Plot of the measured x-component of velocity u versus time t for a uniform flow with velocity components (U,V,W) = (1,0,0). The effect of the number of points M used in the moving-least-square differentiation procedure on the smoothness and accuracy of the differentiation is demonstrated, using computations with M = 1 point (red squares), two points (blue circles), and 5 points (green gradients) on each side of the target point

3 Validation with synthetic data

Section 3 presents findings from validation tests of the MR-PTV algorithm using synthetic data obtained by numerical solution of the particle motion in either a prescribed or computed flow field. Cases with particles in both uniform flow and homogeneous isotropic turbulence are examined.

3.1 Generation of synthetic image data

A synthetic camera code was developed to map 3D particle positions to a 2D image plane. Images of the 3D particle transport are produced as image pairs from a set of stereo “synthetic cameras”. Each camera has a prescribed focal length f, diagonal field of view FOV, and X and Y pixel resolutions $N_{pix,X}$ and $N_{pix,Y}$. The baseline distance between the stereo synthetic cameras is denoted by h.

A cube of unit dimensionless side length was selected as the computational domain, consistent with our decision to non-dimensionalize distances by the computational domain depth L. The computational domain was randomly seeded with N particles with uniform diameter d. A particle with global position ($x_{n} ,y_{n} ,z_{n}$) was mapped to a two-dimensional bitmap with center at position ($X_{n}^{L} ,Y_{n}^{L}$) in the left camera and ($X_{n}^{R} ,Y_{n}^{R}$) in the right camera. Mapping each camera is performed by defining a 3D "camera" coordinate system ($x_{C} ,y_{C} ,z_{C}$) and translating the global coordinate system such that the origin coincides with the camera lens center and rotating the global coordinate system such that the z-axis aligns with the camera lens axis. We use particle position in the camera coordinate system to determine the corresponding particle center position in the image plane using the mapping

$$X_{n} = \frac{{fx_{C,n} }}{{z_{C,n} }}, \quad{Y_{n}} = \frac{{fy_{C,n} }}{{z_{C,n} }},$$

(13)

where f is the camera focal length. The apparent diameter D_n and brightness B_n of particle n in the image plane are given by

$$D_{n} = \frac{fd}{{R_{n} }}, \quad{B_{n}} = \frac{\ell }{{4\pi R_{n}^{2} }},$$

(14)

where $R_{n}$ denotes the distance between the centroid of particle n and the origin of the camera coordinate system (i.e., the center of the camera lens) and $\ell$ is a prescribed particle illumination coefficient. Particles closer to the camera appear both larger and brighter in the images than more distant particles, as shown in Figs. 3 and 4.

Pixels in the computationally generated images that are completely covered by a particle n have intensity set to the particle image brightness $B_{n}$, while pixels that are not covered by a particle images have pixel intensity zero. For pixels that are partially covered by a particle image, the pixel intensity is approximated using a two-dimensional version of the edge length method proposed by Galindo-Torres (2013). In this algorithm, the fraction $\varepsilon$ of the pixel cell area covered by a particle image, is estimated using the sum of the pixel cell edge lengths $\ell_{p,i}$ covered by the particle image divided by the total pixel edge length, or

$$\varepsilon \approx \sum\limits_{i = 1}^{4} {\ell_{p,i} /4\Delta X_{pixel} }.$$

(15)

The pixel intensity for partially-covered images is then set equal to $\varepsilon {\kern 1pt} B_{n}$.

3.2 Validation test for uniform flow

We performed computations using $N = 100$ particles of dimensionless diameter $d = 0.015$ in a uniform flow with prescribed particle velocity components ($u,v,w$) = (1,0,-1). Synthetic cameras with dimensionless baseline separation $h = 0.1$ and focal length $f = 0.01$ output stereo image pairs with a frame rate $\Delta t = 0.01$ and 720 × 960 pixel resolution. For any given frame, the velocity vector of a particle is only calculated if the particle appears in the image of both cameras for M = 5 frames on each side of the current frame, where M is the number of frames used on each side of the given frame in the moving least squares differentiation method shown in Sect. 2.4.

Particle velocity predictions from the MR-PTV algorithm are shown in Fig. 10a for a series of 10 frames as a function of particle depth z. The computational predictions compare well with the exact velocities, indicated in the figure by dashed lines for each velocity component. Figure 10b shows the root-mean-square value of each velocity component, normalized by the free-stream velocity U, as functions of particle depth z. The root-mean-square error was computed in each of a series of 20 bins in the z coordinate spanning the channel width. The data shows the error for each velocity component increases with increase in the particle depth z. The root-mean-square error of the out-of-plane velocity component w is roughly 2–3 times greater than that of the in-plane velocity components u and v. Higher error for the out-of-plane velocity component is typical of PIV/PTV systems, as discussed for stereoscopic particle image velocimetry by Prasad (2000).

Fig. 10

In a, the computed particle velocity components in the x, y, and z directions, denoted by u (red circles), v (green deltas), and w (blue squares), respectively, are shown as functions of the particle depth from the camera. The dashed lines are the exact values of known particle velocities. In b, the root-mean square velocity is plotted for each component as functions of particle depth

3.3 Validation test for isotropic turbulence

Validation tests were conducted for synthetic data using neutrally buoyant particles in an isotropic turbulent flow to examine a flow field in which nearby particles observed on the image plane have very different velocities. Direct numerical simulations of isotropic, homogeneous turbulence were obtained using a triply-periodic pseudo-spectral method with second-order Adams–Bashforth time stepping and exact integration of the viscous term (Vincent and Meneguzzi 1991). Forcing of the turbulent flow was assumed to be proportional to the fluid velocity (Lundgren 2003; Rosales and Meneveau 2005).

The turbulence kinetic energy q and dissipation rate $\varepsilon_{diss}$ were obtained from the power spectrum $e(k)$ as

$$q = \int_{0}^{{k_{\max } }} {e(k)dk} \,, \quad{\varepsilon_{diss}} = 2\nu\int_{0}^{{k_{\max } }} {k^{2} e(k)dk}.$$

(16)

where integration over the wavenumber k is conducted out to a maximum value $k_{\max }$ determined by the resolution limitations of the computation. Various dimensionless measures describing the turbulence in the validation computations are shown in Table 1, including the integral velocity scale $u_{0}$, the average turbulence kinetic energy q, the integral length scale $\ell_{0} = 0.5\;u_{0}^{3} /\varepsilon_{diss}$, the Taylor microscale $\lambda = (15\nu /\varepsilon_{diss} )^{1/2} u_{0}$, and the Kolmogorov length scale $\eta = (\nu^{3} /\varepsilon_{diss} )^{1/4}$. The corresponding microscale Reynolds number is ${\text{Re}}_{\lambda } = u_{0} \lambda /\nu = 99$.

Table 1 Dimensionless simulation parameters and physical parameters of the fluid turbulence

Performance of the MR-PTV system in turbulent flow was evaluated computationally using the same matching coefficients as Sect. 3.2, with N = 100 computational particles, dimensionless camera baseline distance h = 0.1, image resolution 720 × 960 pixels, and time step $\Delta t = 0.01$ between frames. Particles are neutrally buoyant tracers advected by the flow field, with diameter d = 0.015. The velocity field was evaluated using the MR-PTV system for a series of 40 frames.

A comparison of the MR-PTV predictions for the three particle velocity components and the known particle velocities is given in Fig. 11a-c, where each scatter point represents a particle velocity at a given time. Figure 11d shows root-mean square error for each velocity component as a function of particle depth z, where the root-mean square of the particle velocities was evaluated within each of a series of 20 bins on the z-axis. Like the uniform flow computational results in Sect. 3.2, we observed an increased root-mean square error for the out-of-plane z-component of velocity compared to the in-plane x- and y-components, with the velocity error generally increasing with particle depth z.

Fig. 11

a-c Scatter plots comparing the x-velocity, y-velocity and z-velocity components, respectively, of particles in an isotropic turbulent flow computed using the MR-PTV algorithm versus the known particle velocity. d Root-mean-square error in predicted velocity as a function of particle depth z. The x, y, and z directions are denoted by u (red circles), v (green deltas), and w (blue squares), respectively

4 Experimental Validation

Experimental validation tests of the MR-PTV algorithm were performed for uniform flow in a wind tunnel and for flow past a sluice gate in a hydraulic flume. These tests are shown in the subsections below.

4.1 Uniform flow wind tunnel validation

4.1.1 Uniform flow experimental method

An experimental validation procedure was conducted to measure the velocity of expanded polystyrene foam particles flowing in an open return wind tunnel using a HoloLens 2 MR headset oriented perpendicular to the direction of flow. Particles were seeded using a particle hopper, which spanned the cross-section of the wind tunnel. The hopper rested on top of the wind tunnel and the particle feed rate was controlled manually by sliding a cover plate that allowed particles to fall into the wind tunnel. Expanded polystyrene foam particles with diameter d = 4.18 ± 0.38 mm were used. Diameter measurements were obtained by measuring the diameter of 50 particles using digital calipers. The particle settling velocity was calculated by measuring a series of 50 foam particles falling 2.0 m at terminal velocity. Flow speed inside the wind tunnel was controlled by the fan speed at the end of the open return wind tunnel. The fluid velocity component x-direction was measured using a hot wire anemometer positioned at the midline of the wind tunnel. Horizontal wind velocity measurements were consistent throughout all areas of the observed test section. A black background curtain was placed at a depth of 110 cm from the camera.

Images were captured using two front-facing visible light cameras on the Microsoft HoloLens 2 mixed reality headset. The stereo cameras are co-directional, synchronized, and separated by a baseline distance h = 9.9 cm. Each camera had video resolution of 480 × 640 pixels and a framerate of 30 Hz. A checkered calibration board was used to verify the camera configuration. The MATLAB stereo camera calibrator app was used to validate that intrinsic and extrinsic camera parameters matched the manufacturing details. Next, we extracted particle images from the HoloLens 2 and processed externally using the MR-PTV algorithm shown in Sect. 2. A limitation of the Microsoft HoloLens 2 is a fixed frame rate of 30 Hz. The fixed camera frame rate makes it more difficult to track and link particles, because a single particle appears in fewer frames and travels a greater distance between frames. Given this limitation, the wind tunnel results were performed using only M = 2 nearest points in the moving least squares gradient filter.

4.1.2 Results

Results from the wind tunnel experiment are shown in Fig. 12. Velocity components are plotted against depth from camera on the horizontal axis. Black dashed lines represent the expected velocity readings (u, v, w) = (1.52, − 1.37, 0) m/s, given by the fluid velocity, the particle sedimentation velocity, and zero, respectively. The root-mean-square values of the velocity measurements are shown in Table 2. The root-mean-square error for the out-of-plane velocity, w, is nearly double that of the in-plane velocity, u, consistent with results from synthetic data in Sect. 3. Table 2 shows agreement between the average MR-PTV velocity component measurements and experimentally measured comparison values of velocity.

Fig. 12

Particle velocity measurements for uniform wind tunnel flow from MR-PTV with three data frames. Red circles, green triangles, and blue squares represent particle x, y, and z velocity components, respectively. Comparison velocities are indicated with dashed lines

Table 2 Average and root-mean square values from MR-PTV measurements for the uniform flow wind tunnel test. Comparison values are the measured particle velocity based on the measured fluid velocity for u, particle sedimentation velocity for v, and zero induced velocity in w

4.2 Sluice gate flume validation

4.2.1 Experimental method

Experimental validation was performed by imaging particles advected by flow in an open channel hydraulic flume. The flume had a width of 50 cm and was filled with water to a height of 40 cm with an outer rectangular footprint of 3.9 × 2.0 m. A motor-controlled water wheel was used to generate flow. Rigid guide vanes were fixed in each corner of the flume to maintain flow uniformity. A honeycomb steel mesh, inserted upstream of the test section, served as a flow conditioner. The flume had a sluice gate body, with a thickness of 1.0 cm, inserted in the flow 26 cm below the water surface. Particles were introduced into the flow using a perforated aluminum hopper fixed 2 mm above water surface. The hopper spanned 33.7 cm across the width of the flume and 22.3 cm in the direction of flow. The hopper midpoint was 57 cm upstream of the camera center.

The flow was seeded with multi-colored spherical water gel particles (Spin Master). Using digital calipers to measure particle diameter for a set of 50 particles, the average particle diameter was found to be $d =$ 10.6 ± 1.3 mm. The water wheel rotation rate controlled free-stream fluid velocity. The comparison particle velocity in the horizontal x-direction in the test section was determined by tracking the time required for a particle to traverse a fixed horizontal distance (0.9 m), yielding a horizontal particle velocity estimate of u = 0.0983 ± 0.005 m/s. The particle sedimentation velocity in the y-direction was measured by tracking the time required for the particle to fall a fixed distance (0.7 m) at terminal velocity, yielding a particle vertical velocity of v = 0.0374 ± 0.003 m/s. The reported uncertainty values were based on the root-mean-square of 25 repeated tests for both u and v. By comparing measured particle sedimentation velocity to the theoretical terminal velocity of the particles, obtained using the Schiller-Naumann drag formula for a sphere (Schiller and Naumann 1933), we estimated the effective density of the particles to be $\rho_{p} =$ 1.006 g/ml.

Images were again captured using two front-facing visible light cameras on the Microsoft HoloLens 2 mixed reality headset. The headset was fixed to a mannequin head aligned perpendicular to the direction of flow with 49 cm between the camera lens and the flume mid-section. Corrections to particle positions accounted for refraction at the flume wall using the refraction correction algorithm of Bao and Li (2011).

4.2.2 Computational approach

This section describes the method used to obtain a numerical solution for fluid and particle velocity around a partially submerged sluice gate, which was used to obtain data to compare with the experimental MR-PTV data. We used ANSYS Fluent finite-volume computational fluid dynamics (CFD) to model incompressible fluid flow in the flume domain and extracted the steady-state fluid velocity field for a simulation of water flowing past a submerged sluice gate. The CFD simulation used a 2D domain, modeled to match the flow inside the flume. The origin of the computational domain is set to the perpendicular position of the HoloLens origin during the experiment. Figure 13 shows boundary conditions used in the simulation. The right wall of the domain is a flow velocity inlet with uniform velocity set to the free-stream flow velocity inside the flume (u = 0.0983 m/s), and the left wall is a pressure outlet. The bottom surface and the sluice gate are no-slip wall boundaries. The top wall of the domain is a fixed, free-shear surface. Our experiments showed that at the low fluid flow rates used in the validation tests, the fluid height difference between the upstream and downstream sides of the side gate were negligible. A uniform Cartesian mesh was used with 2020 elements in the x direction and 800 elements in y direction. Convergence with relative error of less than 10^–6 was reached for both velocity components. Grid independence was demonstrated using both coarser and finer grids and by comparing the velocity field.

Fig. 13

Domain boundary conditions used in CFD simulation, where the origin is where the Microsoft HoloLens 2 was positioned perpendicular to the domain

Theoretical particle motion was determined by solving the particle momentum equation

$$(m + m_{A} )\frac{{d{\mathbf{v}}}}{dt} = - 3\pi \mu \,d({\mathbf{v}} - {\mathbf{u}})f_{I},$$

(17)

where $m_{A} = 0.5\rho_{f} V$ is the particle added mass, m, V and d are the particle mass, volume and diameter, $\mu$ and $\rho_{f}$ are the fluid viscosity and density, v and u are the particle and fluid velocity vectors, and

$${\text{Re}}_{p} \equiv \frac{{\rho_{f} d\left| {{\mathbf{v}} - {\mathbf{u}}} \right|}}{\mu }$$

(18)

is the particle Reynolds number. The factor

$$f_{I} = 1 + 0.15{\text{Re}}_{p}^{0.687}$$

(19)

is an inertial correction factor (Schiller and Naumann 1933), which is valid for ${\text{Re}}_{p} < 800$. We set all values used in the particle momentum equations to match experimental conditions. Here we include the particle inertia and the added mass and drag forces. Other forces on the particles, such as lift, pressure gradient, and history forces, are negligible under the conditions used in the flow computations (Marshall and Li 2014).

For the current sluice gate validation, computational particles were initialized in a horizontal rake on the right-hand side of the computational domain, matching the physical location, where particles were released from the aluminum hopper during the experiment. We determined theoretical particle path lines by tracking the particle positions across the computational domain.

4.2.3 Results

Velocity measurement results using the MR-PTV system and the computed particle velocity fields are shown in Fig. 14. In Fig. 14a, the direction of the experimental MR-PTV velocities, at each measured particle position, are compared to the computed particle path lines, where particle positions and experimental particle velocity direction vectors are plotted overlying a color plot with path lines of the computed fluid velocity field from Sect. 4.2.2. The sluice gate is shown as a vertical white bar protruding into the flow. In Fig. 14b, the velocity magnitude of the experimental MR-PTV velocities are compared to magnitudes of the computed particle velocities from Sect. 4.2.2 at the same locations.

Fig. 14

MR-PTV measured velocity vectors for flow past a sluice gate. a Scatter plot showing experimental particles (yellow) with MR-PTV velocity direction (black arrows) superimposed onto CFD contour plot of velocity field for flow past a sluice gate, with computed particle path lines indicated by black lines. b Comparison of velocity magnitude at particle locations as measured experimentally using the MR-PTV algorithm (y-axis) to simulated velocity magnitude by solving the particle momentum equation with the computed velocity field (x-axis)

The overall comparison of experimental MR-PTV data and computational data in Fig. 14 show good agreement. Most of the experimental MR-PTV velocity vectors in Fig. 14a are oriented along the computed particle path lines, although there is some vector scatter in a few instances. The computational predictions for particle velocity magnitudes are within about 10% of the experimental values obtained from the MR-PTV algorithm (Fig. 14b). While the agreement is close, we do see in Fig. 14b that the MR-PTV predictions underestimate the velocity magnitude relative to the computational predictions. This underestimate is on the order of magnitude of the accuracy of the computational model of particle motion used for comparison to the MR-PTV data.

5 Conclusions

We present a particle tracking velocimetry system compatible for use with a mixed-reality headset, such as the Microsoft HoloLens 2. The system uses video feed from two co-directional, synchronized, stereo cameras to detect and track particles through time to estimate the three-dimensional particle velocity vectors. Adaptive thresholding is used to detect particles in individual images. A stereo matching algorithm is optimized for three-dimensional flow fields using monocular cues, such as brightness, depth, and apparent velocity, to match particles between stereo images. Distance estimate is performed using binocular disparity. A moving least squares gradient filter uses a time series of particle images to reduce noise in performing time differentiation of the particle position in estimating particle velocity.

The approach was validated both computationally using synthetic data and in laboratory experiments. Synthetic data was used to perform a detailed error analysis for determination of particle depth from the camera. Three major sources of error were identified, including pixel resolution of the particle image, baseline distance between the cameras relative to the overall flow dimension, and particle overlap in an image. The error in depth estimation was found to increase substantially when the camera baseline distance is less than 2% of the measurement depth and when the apparent image size of particles is less than 10 pixels. We then used synthetic data to examine accuracy of MR-PTV velocity estimates for particles in uniform flow and in isotropic turbulence, and for both in-plane and out-of-plane particle velocity components. The error generally increased with distance of the particle away from the camera, with higher error for the out-of-plane component.

The MR-PTV approach was experimentally validated using the Microsoft HoloLens 2 mixed reality headset to image particles convected in a wind tunnel and particles flowing around a submerged sluice gate in a hydraulic flume. Mean MR-PTV measurements compared very well with comparison velocity in the wind tunnel tests. The direction of MR-PTV computed velocity vectors agreed with computed particle path lines for particles flowing around a sluice gate body, although with some directional scatter. The magnitude of the experimental MR-PTV velocity vector measurements for the sluice gate flow was within 10% of computed particle velocities, which was within estimated uncertainty of the numerical computations.

The advantage of the proposed MR-PTV algorithm is that velocity measurement can be achieved with only a mixed reality headset and appropriate flow seeding. The seeds can be either synthetic or natural (e.g., snowflakes), and do not need to be highly spherical. This is a stark contrast to most existing 2D or 3D laboratory-based PTV systems, which are typically designed for precision measurements in controlled laboratory settings and require expensive specialized equipment (lasers, multiple cameras, synchronizers, etc.). The proposed MR-PTV algorithm uses monocular artifacts of non-uniformity, which may be present in a natural environment, to match particles between stereo images, which when combined with binocular disparity can generate reasonably accurate velocity estimates without requiring additional specialized equipment. While we have successfully demonstrated and validated the proposed algorithm in the current paper, it is also clear that the use of this algorithm is currently restricted by hardware limitations of the headset cameras in these early generation mixed reality devices. With further improvements in camera resolution and frame rate in mixed reality headsets, the MR-PTV approach has promise for use as a simple particle velocity visualization tool in a variety of industrial, entertainment, and scientific applications.