1 Introduction

One of the most characteristic flow phenomena in a rotating system is the emergence of Taylor columns. A Taylor column is an isolated two-dimensional fluid region uniform along the axis of system rotation, which was first recognized experimentally by Taylor (1917, 1923). A schematic view of his experiment is shown in Fig. 1. In this experiment, a fluid-filled container rotates rapidly around a vertical axis while a three-dimensional object moves slowly through a driving screw fixed inside the container. By dye visualization, he showed the existence of a vertically uniform two-dimensional fluid region above the object, the surface of which dye does not traverse.

Fig. 1
figure 1

Experiment on Taylor columns in a rotating container by Taylor (1923)

Full size image

Not only in a closed container, a similar situation is encountered in an open flow, for example, a horizontally parallel flow in which a three-dimensional object is submerged. Under a system rotating about a vertical axis, the disturbance by the submerged object to the parallel flow may not be localized around it, and a vertically uniform isolated region, that is, a Taylor column, may appear.

The theoretical background is briefly described here. We consider an incompressible flow between horizontal boundaries with the depth H, in which a circular cylinder of the diameter D and the height h (< H) is placed on the bottom, fixed to a system rotating with respect to a vertical axis at a constant angular velocity \(\Omega\). The coordinate system used here is the Cartesian system fixed to the vertically rotating system, which consists of the x-axis in the streamwise, y-axis in the spanwise and z-axis in the vertical direction. The horizontal and vertical coordinates are normalized by D and H, respectively. The (x, y, z) components of the velocity u of the fluid are denoted by (u, v, w), and the pressure by p. The representative velocity in the streamwise direction is denoted by U. We normalize the horizontal and vertical velocity components by U and UH/D, and the time t by D/U. We then obtain the governing equation:

$$\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} + \frac{\partial w}{{\partial z}} = 0} \\ \end{array}$$
(1)
$$\begin{array}{*{20}c} {Ro\left( {\frac{\partial u}{{\partial t}} + \left( {{\varvec{u}} \cdot \nabla } \right)u} \right) - sgn\left( {\Omega } \right) v = - \frac{\partial p}{{\partial x}} + \frac{Ek}{2}\left[ {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \delta^{2} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)} \right] , } \\ \end{array}$$
(2)
$$\begin{array}{*{20}c} {Ro\left( {\frac{\partial v}{{\partial t}} + \left( {{\varvec{u}} \cdot \nabla } \right)v} \right) + sgn\left( {\Omega } \right) u = - \frac{\partial p}{{\partial y}} + \frac{Ek}{2}\left[ {\frac{{\partial^{2} v}}{{\partial z^{2} }} + \delta^{2} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)} \right] ,} \\ \end{array}$$
(3)
$$\begin{array}{*{20}c} {\delta^{2} Ro\left( {\frac{\partial w}{{\partial t}} + \left( {{\varvec{u}} \cdot \nabla } \right)w} \right) = - \frac{\partial p}{{\partial z}} + \frac{{\delta^{2} Ek}}{2}\left[ {\frac{{\partial^{2} w}}{{\partial z^{2} }} + \delta^{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)} \right] .} \\ \end{array}$$
(4)

Equations (1–4) are respectively the continuity equation and the Navier–Stokes equations in the rotating system. The dimensionless parameters in Eqs. (2–4) are defined by

$$\begin{array}{*{20}c} {Ro \equiv \frac{U}{{2D\left| {\Omega } \right|}}, Ek \equiv \frac{\nu }{{H^{2} \left| {\Omega } \right|}}, \delta \equiv \frac{H}{D},} \\ \end{array}$$
(5)

where \(\nu\) is the kinematic viscosity of the fluid. Here the density of the fluid is set to unity, and the pressure p is normalized by \(2UD\left|\Omega \right|\). The gravitational and centrifugal forces are included in the pressure gradient terms by incorporating their potentials \(gz\) and \(-\frac{1}{2}{\Omega }^{2}[{\left(x-{x}_{c}\right)}^{2}+{\left(y-{y}_{c}\right)}^{2}]\) to p, where g is the gravitational acceleration and \(({x}_{c}, {y}_{c})\) is the location of the axis of system rotation. The parameters \(Ro\) and \(Ek\) defined in Eq. (5) are called Rossby number and Ekman number, respectively. If both of \(Ro\) and \(Ek\) are small, we may obtain the zeroth-order equation from Eqs. (2–4) as

$$\begin{array}{*{20}c} {\varvec{k} \times \varvec{u} = - \nabla p,} \\ \end{array}$$
(6)

where \({\varvec{k}}\equiv (0, 0,1)\) is the unit vector in the z direction. Taking the rotation of the both sides of Eq. (4) and applying the continuity Eq. (1), we find the homogeneity of the velocity field in the z direction, as

$$\begin{array}{*{20}c} {\frac{{\partial {\varvec{u}}}}{\partial z} = 0.} \\ \end{array}$$
(7)

This result is known as the Taylor-Proudman theorem (Proudman 1916; Taylor 1917) and gives theoretical support for the emergence of Taylor columns in a rotating flow.

As seen in the derivation of Eq. (7), a Taylor column is not necessarily present in any rotating system. Hide and Ibbetson (1966) pointed out that the critical Rossby number is given by the ratio h/H for the genesis of a Taylor column. Huppert (1975) then suggested a concrete expression of the critical Rossby number that depends on the shape of the submerged object, based on an asymptotic analysis for which geostrophic flow (6) holds. Applying to our case of a flat-topped cylinder, we obtain the criterion as \(2Ro<h/H\). An experiment in a rotating tank by Hide & Ibbetson (1966) showed that a Taylor column exists not directly over the submerged object, but, is displaced downstream. It was also found that the flow inside the Taylor column consists of a single vertical vortex, and its horizontal scale is smaller than that of the submerged object.

As Taylor called it ‘virtual cylinder’, the existence of such an isolated region affects the flow passing around. Under a steady horizontal incoming flow, vortex-shedding from a Taylor column may also occur. In a stably stratified fluid, Huppert and Bryan (1976) showed the existence of a critical incoming velocity above which cyclonic (rotating in the same direction as the system) vortices are shed and advected downstream. On the other hand, vortex-shedding of both cyclonic and anti-cyclonic vortices from a Taylor column has also been observed experimentally in a curved current in a circular rotating tank (Takematsu and Kita 1978; Leader 1992), and numerically above a submerged bluff body (Khaledi and Andersson 2010), which show a characteristic wake flow reminiscent of the well-known Karman’s vortex street.

In nature, this type of flow is typically found in planetary boundary layers (Hide 1961), where not only the system rotation but also stable stratification in the vertical direction is important. In laboratory experiments, it was shown that the length of a Taylor column is reduced by the stratification (Davies 1972). However, since Taylor columns hardly emerge in the Earth’s atmosphere (Stone and Baker 1968), the influence of the system rotation and stratification on the wake at the levels below the top of the topography has been mainly concerned. Under strong enough stratification for the Froude number (\(\equiv U/Nh\), where N is the Brunt-Vaisala frequency) less than 0.4, contour-rotating vortices are observed to be shed alternately behind a topography. The effect of rotation also contributes to the emergence of vortex-shedding (Boyer et al. 1987), while Etling (1990) concluded that stable stratification is essential by comparing the existing laboratory experiments and atmosphere observations. A wake flow exhibiting vortex-shedding of an isolated large island was also examined in detail by a numerical model (Ito and Niino 2016). Furthermore, the vertically decoupling behavior of vortices behind an idealized seamount for further stronger stratification was demonstrated numerically (Perfect et al. 2018).

In contrast, the wake of a Taylor column in a homogeneous rotating flow has been less intensively studied. Especially for a realistic flow of finite Rossby and Ekman numbers, the conditions for whether Taylor columns emerge and, if any, how vortices are shed from Taylor columns have not been revealed. Furthermore, in experimental studies, the main flow passing by the submerged object is typically not straight but curved in a circular duct or circular container, where the effect of the curvature of the streamlines must be considered. Avoiding this effect, we conducted experiments in a straight channel flow long enough to observe a Taylor column and its wake on a large turn table whose rotating speed can be controlled well. This paper aims to clarify the criterion for the emergence of Taylor columns and their influence on the wake under finite values of the system parameters through a visualization and velocity measurement of the surface flow.

2 Experiment

2.1 Rotating open-channel

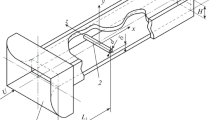
We here consider an open-channel flow in a rotating system (see Fig. 2a and b). The origin of the horizontal (x, y) plane is fixed to the rear end of the horizontal section of the submerged cylinder. The open channel with W = 346 mm and H = 100 mm is embedded within a circular open container of the diameter 1200 mm, as in Fig. 2c. A flow through the channel is driven by two screws placed at each path outside the channel. In these side paths, some cubic blocks taller than the fluid depth are also placed to dampen the surface waves generated by the rotation of the screws. On the upstream side of the channel, a rectifier section made of plastic pipes with 9 mm of diameter is placed. A cylinder is submerged at the center of the channel about 200 mm downstream from the exit of the rectifier. Water at room temperature is used as the working fluid. The container is placed on a circular turn table with 6 m of diameter at Meteorological Research Institute (See Fig. 3). In the present experiments, the turn table was operated at the angular velocity \(\Omega\) up to 4 r.p.m.

Fig. 2
figure 2

a Side- and b top-views of the open channel with a submerged cylinder, c Experimental setup. Point C in c indicates the axis of system rotation, which coincides with the center of the container

Full size image
Fig. 3
figure 3

Rotating table at Meteorological Research Institute

Full size image

2.2 Velocity measurement on surface

We measured the velocity field (u,v) on the free surface of the open channel by a Particle Image Velocimetry (PIV) technique. For the tracer, we used Lycopodium powder with the mean diameter of 35 \(\mu\) m and the density of 1.05 \({{\text{g}}/{\text{cm}}}^{3}\). The surface was recorded by a camera (Victure, AC700) fixed to the turn table at 30 fps with the resolution of 3840 \(\times\) 2160 pixels. An example of the raw images is shown in Fig. 4a. After removing the radial distortion (Zhang 2000) from the raw images, we clipped the image of 458 \(\times\) 208 pixels that covers the horizontal physical area of \(640\times 284 {{\text{mm}}}^{2}\) on the free surface, a sample of which is shown in Fig. 4b. The bottom and sidewalls of the channel are painted in black so that the powder on the surface can be recognized well under incandescent electric lamps. Any laser equipment was not used in the present experiments. The image processing was done using 16 \(\times\) 16 interrogation windows with 50% overlaps in both the x and y directions. The time interval between the two frames to be processed is 0.5 s. The resulting spatial resolution is 11 mm. The PIV was carried out by a standard cross-correlation method implemented by Python. Figure 5 shows an example of the velocity profiles of the streamwise and spanwise velocities obtained by the PIV measurement for the case of \(\Omega =0\). It is confirmed that the flow on the free surface of the open channel resembles the Poiseuille flow between two parallel flat plates. The streamwise velocity at the center of the channel is used as the representative velocity U. The velocity scale U for non-zero \(\Omega\) is given by that for the case of \(\Omega =0\) with the same values of the other parameters (h, D) and the power supply to the driving motors. The parameters for the conducted experiments are listed in Table 1.

Fig. 4
figure 4

An example of pictures used for a PIV analysis. a The original, and b the undistorted and cropped one used for the analysis

Full size image
Fig. 5
figure 5

Profiles of the streamwise and spanwise velocities \((u, v)\) on the surface for \(\Omega =0\) as functions of the spanwise coordinate y at \(x=2\) (blue), 4 (light blue), 6 (green) and 8 (orange) for the case of D = 45 mm. Dashed curves indicate the Poiseuille flow between two parallel planes

Full size image
Table 1 Parameters of the experiments
Full size table

The fine flow structures in and around a Taylor column, if any, cannot be resolved well by the obtained velocity field due to the coarse resolution of our measurement. We here limit ourselves to detecting the emergence of a Taylor column and the following vortex-shedding, and to computing its frequency, for which the present data set is useful.

3 Results

3.1 Emergence of a steady vortex and vortex-shedding

For our Reynolds number \(Re\equiv UD/\nu =2Ro/{\delta }^{2}Ek\) in the order of \({10}^{2}\), the flow is expected to be laminar. When \(Ro\) and \(Ek\) are large enough, the free surface flow is unaffected by the three-dimensional disturbances generated around the submerged cylinder on the bottom. As \(Ro\) is decreased by increasing \(\Omega\), the influence of the submerged cylinder on the surface flow may become apparent. For the flow with the Rossby number slightly below unity, while the streamlines seem parallel to the streamwise direction right above the cylinder, the flow is slightly curved and slowed down about 2D downstream from the cylinder, as shown in Fig. 6a. If \(Ro\) is further decreased, a steady vortex appears, and, more interestingly, vortices are periodically generated and released downstream from the steady vortex. Figure 6b, c respectively show the time-averaged velocity field \((\overline{u }, \overline{v })\) for \(Ro=0.36\) and 0.18, where the periodic motion of vortex-shedding is smoothed out, and only the steady vortex is emphasized. In these cases, the location of the steady vortex deviates from the center of the channel toward the negative side y < 0, and the direction of the rotation coincides with that of system rotation, that is, cyclonic. In Fig. 6, the contours of the vertical vorticity \({\omega }_{z}\) on the surface are superposed. For all the cases, we find that the magnitude of the vorticity is large in the both spanwise sides of a stagnant region whose streamwise position becomes closer to the submerged cylinder as the Rossby number decreases. In the time-dependent cases (b) and (c), these large-vorticity regions are located steadily in the same position as well as the steady vortex in between. After the steady vortex, clockwise and counter-clockwise vortices are alternately generated and released almost along a single line. A dye visualization of the surface flow for such cases, shown in Fig. 7a, is reminiscent of the well-known vortex-shedding in the two-dimensional cylinder wake for \(Re\approx 300\) (Williamson 1996). The snapshots of the velocity fields subtracted by the mean, \((u-\overline{u }, v-\overline{v })\), clearly show a vortex-street advected downstream, as shown in Fig. 7b–d.

Fig. 6
figure 6

Velocity (u, v) and vertical vorticity \({\omega }_{z}\) field on the water surface for a \(Ro=0.72\), b 0.36 and c 0.18. For all the cases, \(Re=291\) and \(h/H=0.5\). For the unsteady cases (b, c), the time-averaged velocity \((\overline{u },\overline{v })\) and vorticity \(\overline{{\omega }_{z}}\) are shown. The red circles indicate the location of the submerged cylinder. The coordinates are normalized by the diameter of the submerged cylinder

Full size image
Fig. 7
figure 7

a Visualization of a vortex-street on the surface over a submerged cylinder, and b, c snapshots of the fluctuating velocity \((u-\overline{u }, v-\overline{v })\) and the vertical vorticity \({\omega }_{z}-\overline{{\omega }_{z}}\) field on the surface. c and d are the snapshots at T/3 and 2 T/3 later from (b). The red circles in b–d indicate the location of the submerged cylinder. The parameters are \(Re=291\), \(Ro=0.18\) and h/H = 0.5. The coordinates are normalized by the diameter of the submerged cylinder

Full size image

Equation (7) implies that the surface flow is a horizontal cross-section of the two-dimensional flow in the inviscid region. Therefore, the observed vortices on the surface evidence the existence of vertically uniform two-dimensional vortices, as illustrated in Fig. 8. The steady vortex behind the submerged cylinder is considered a Taylor column originally observed in Taylor’s experiment (Taylor 1923). This virtual cylinder presumably triggers the vortex-shedding. The fluctuating vertical vorticity field on the surface is also shown in Fig. 7b, c, though it should be noted that, due to the coarse measurement of the velocity field by the present PIV, the computed fluctuating vorticity captures only spatially large-scale variations. We can find that positively and negatively large-vorticity regions are alternately released and advected downstream. Though the vortex-shedding observed here seems similar to that behind a two-dimensional cylinder, the mechanism to supply the vorticity in the present system must be different because of the absence of the solid no-slip boundary (Sun & Chern 1994).

Fig. 8
figure 8

A schematic view of the vertical vortices behind a submerged cylinder in a rotating system

Full size image

If the system rotation is reversed, the steady vortex also becomes reversed and is located in the range of \(y>0\). These facts are simply justified by the symmetry of the system. The Ekman pumping transfers the cyclonic vertical vorticity upward, contributing to the creation of the steady vertical vortex in the inviscid region. The steady vortex is therefore generated above the region where cyclonic vorticity is significant, that is, \(y<0 (>0)\) when \(\Omega >0 (<0)\). A likely related flow is the wake of a two-dimensional rotating cylinder. In such a flow, the rate of the surface speed of the cylinder to that of the incoming flow is small, say, less than 1.5, a vortex street occurs with the inclination to the x-axis (Mittal & Kumar 2003). In the present cases, any significant inclination of the vortex street was not recognized while the averaged vorticity field on the surface was found to be asymmetric with respect to the x-axis, as shown in Fig. 7b, c.

3.2 Conditions for the emergence of vortex-shedding

To investigate the conditions for the development of a periodic flow involving vortex-shedding in the present system, we carried out experiments for several values of \(Ro\), Re and two values of h/H. Figure 9 shows the cases acquired in the present experiments by closed circles on the \((Ro, Re)\) plane. For h/H = 0.25, the vortices appear only in the case of \(Ro=0.15\) and Re = 225. For the case of h/H = 0.5, the vortices are observed approximately for \(Ro\lesssim h/2H\) and \(Re\gtrsim 100.\) The present experiments provide a consistent result to Hide and Ibbetson (1966) and Huppert (1975) for the critical value of the Rossby number, and also imply that Reynolds number must be large enough. The thresholding value of the Reynolds number seems to depend on h/H, but the detail still needs to be clarified.

Fig. 9
figure 9

Observed types of the surface flow on the parameter plane \((Re,2Ro)\) for a h/H = 0.25 and b 0.5. Blue, steady; red, periodic with vortex-shedding. Strouhal number and the normalized distance between successive co-rotating vortices \((St, \Delta /D)\) are added for each periodic case. The horizontal dashed lines indicate \(2Ro=h/H\)

Full size image

The streamwise periodicity in the wake of the Taylor column was obtained by measuring the distance \(\Delta\) between the peeks of the surface vorticity averaged in the y direction in the range of \(-1.5<y<1.5\). For h/H = 0.5, the distance normalized by D depends slightly on the parameters, as shown in Fig. 9. If we assume the effective diameter D’ of the Taylor column determines the periodicity of the vortices by \(\Delta =4D{\prime}\) as in the vortex-street behind a two-dimensional cylinder for large enough Reynolds numbers, it turns out that D’/D falls within the range from 0.9 to 1.1. Therefore, the size of the Taylor column seems comparable to that of the submerged cylinder for h/H = 0.5. For h/H = 0.25, D’ is noticeably smaller than D.

The frequency f of the vortex-shedding was also computed from the time sequence of a velocity component at an appropriate horizontal location on the free surface. The dimensionless frequency, Strouhal number \(St\equiv fD/U\), is also added in Fig. 9. For the parameters in the present experiments, St varies within the range between 0.1 and 0.3. Given the robustness of the effective size of the Taylor column, one of the reasons for this behavior is that the effective velocity scale associated with the vortex-shedding is governed by the three-dimensional flow structure of/around the Taylor column which depends on Re and Ro. An example is shown in Fig. 6b, c: the mean velocity passing by the Taylor column is faster for larger Ro, even though the power supply to the impellers is the same for these two cases.

The dependence of St on Re and \(Ro\) in the present system is still unclear. A further comprehensive study is required to clarify the three-dimensional flow structure around the Taylor column and the scaling of the frequency of vortex-shedding.

4 Conclusions

We experimentally studied the effect of system rotation on the wake over a submerged cylinder in an open channel. If Rossby number \(Ro\) is small and Reynolds number is large enough, a steady vortex and vortex-shedding from this vortex appear on the free surface. It turns out that vertically uniform steady vortex and periodic vortex-shedding may be present behind a submerged cylinder in a rotating system. A necessary condition for the emergence of these vortices is given by \(2Ro\lesssim h/H\). Reynolds number must be large enough, but the thresholding value depends on h/H.

Under these conditions, the estimated size of the emerging Taylor column is comparable to that of the submerged cylinder for h/H = 0.5 and is noticeably smaller for h/H = 0.25, and the Strouhal number of vortex-shedding ranges approximately from 0.1 to 0.3.

We focus on low values of the Reynolds number for which clear (non-turbulent) vortex-shedding is observed. The dependence on Reynolds number in a wider range is also still open.