1 Introduction

The impact of droplets on solid surfaces is a common occurrence not only in nature, as in the case of raindrops (Kim et al. 2020), but also in various industrial applications, including spray cooling (Zhang et al. 2013; Shahmohammadi et al. 2018; Gultekin et al. 2021), spray coating (Pasandideh-Fard et al. 2002; Ma et al. 2020), and many more. When a droplet impacts a surface, various droplet impact dynamics may occur, including splashing, spreading, receding, and bouncing. These dynamics have been thoroughly reviewed in the literature (Yarin 2006). There have been numerous studies conducted on the topic of droplets impacting on solid surfaces (Liang and Mudawar 2017) or thin liquid films (Liang and Mudawar 2016), as outlined in comprehensive reviews. Spreading radial velocities play a critical role in determining the final outcome of droplet impingement. If the radial velocities are too low, the droplet may not adequately cover the surface, resulting in incomplete coating or inefficient heat transfer. Additionally, measuring spreading radial velocities can provide insights into the underlying physics of droplet impingement. The spreading dynamics of a droplet can reveal information about the interaction between the droplet and the solid surface, as well as the formation of a thin liquid film. Understanding the relationship between these parameters and the radial velocities can aid in designing more efficient droplet impingement systems.

In the literature, there are some studies that show that the radial velocity of an impacting droplet on a surface is linearly related to the spreading radius (Yarin and Weiss 1995; Roisman et al. 2002; Wang and Bourouiba 2017, 2018). Yarin and Weiss (1995) as well as Roisman et al. (2002) have put forth an empirical model for the radial velocity distribution in the lamella,

$$\overline{u} = \frac{{\overline{r}}}{{\left( {\tau + c} \right)}}$$
(1)

where \(\overline{r}\) is dimensionless radius, τ is dimensionless time, and c is a constant. The given expression is applicable specifically for the radial velocity field in the lamella that is formed during the spreading process of a droplet with a high Weber number.

Many previous studies have focused on providing limited quantitative data, such as the spreading diameter of droplets and the height of the lamella. Recent developments in visualization and imaging technology have made important progress in measurement methods, providing more accurate and reliable results. Droplet impingement onto solid surface involves a variety of dynamic processes such as kinetic energy conversion, which occurs in a very short time, and these are crucial mechanisms for understanding the physics of droplet and surface interactions (Jung et al. 2016). One major challenge in studying this process is the difficulty of obtaining non-invasive measurements of physical quantities in the target area. In these cases, the PIV measurement method has been particularly successful to visualize and analyze fluid flow. It involves tracking the movement of small particles within the flow over time and can be used to create animations of the flow. PIV is particularly useful for studying dynamic behaviors and changes in the flow over time (Adrian 2005). It involves measuring the velocity of fluid flow within a specific area. However, obtaining high-quality data using PIV often requires careful attention to factors such as illumination and magnification. Higher magnification can improve the accuracy of the measurements, but it also reduces the size of the field of view and the spatial resolution of the data. This trade-off must be carefully considered when using PIV to ensure that the data collected is of sufficient quality.

In the literature, several researchers have utilized the PIV technique to examine the flow field within liquid droplets. The majority of these researches have concentrated on sessile droplets (Kang et al. 2013; He and Qiu 2016; Morozov et al. 2018; Al-Sharafi and Yilbas 2019). Smith and Bertola (2011) employed PIV to measure the velocity field within droplets impacting on a hydrophobic surface. Frommhold et al. (2015) also used PIV to report on the flow field within impacting droplets on both dry and wetted surfaces. In another study, Erkan and Okamoto (2014) used PIV to study the spreading velocities of a single droplet with low Weber number as it impacted a non-heated glass surface at various impact velocities during the early spreading phase. They observed that the radial velocity exhibits a linear trend over a significant range of spreading radius. Erkan (2019) also investigated the radial velocity distributions within a single droplet with low Weber number as it impacted a heated surface. Gultekin et al. (2020) have investigated a pair of droplets impacting a heated surface under various initial droplet velocities using PIV. They observed the formation of another stagnation point in the interaction area for the droplet pair.

The primary aim of this research was to thoroughly examine the behavior of spreading velocities within droplets over a wide range of Weber numbers using advanced measurement techniques. To achieve this goal, experiments were conducted using droplets with velocities from 0.41 to 2.37 m/s and Weber numbers ranging from 5 to 183. The Weber number \(\left( {{\text{We}} = \frac{{\rho U_{o}^{2} D_{o} }}{\sigma }} \right)\) is a dimensionless parameter that is used to quantify the relative importance of inertial and surface tension forces on a droplet, and it plays a crucial role in determining the spreading behavior of droplets upon impact with a solid surface. In this equation, the density (ρ) and surface tension (σ) of the fluid and the impact velocity (Uo) and initial diameter (Do) of the droplet are variables that can be measured from shadowgraph images. To measure and analyze the spreading velocities of the droplets under these conditions, both time-resolved PIV and shadowgraph techniques were employed. These techniques allow for accurate and precise measurement of the velocities of the droplets as they spread and interact with the solid surface. By carefully controlling the experimental parameters and utilizing advanced measurement techniques, it is possible to gain a deep understanding of the mechanisms governing droplet behavior and how these mechanisms change with the Weber number. The results of this research can be used to inform the design and optimization of a variety of industrial and scientific applications involving droplet impact and spreading.

2 Experimental setup

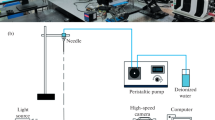
Experimental setup for PIV investigations has been thoroughly described in detail in our former article (Gultekin et al. 2020). However, for the sake of completeness, we will provide a brief overview of the experimental setup and its key components here. Figure 1 shows a schematic diagram of the experimental setup for the PIV experiments. The key components of the PIV system include a laser device and fast cameras. The laser device generates a sheet of laser light that illuminates the droplets as they impact the solid surface, allowing the cameras to capture images of the droplets at high temporal and spatial resolution. The fast cameras, which are synchronized with the laser device, are used to record the images of the droplets, which are then processed using image analysis software to extract the velocity and position information. The experimental setup also includes a droplet generator, which is used to produce droplets with a range of impact velocities and Weber numbers.

Fig. 1
figure 1

Schematic diagram of PIV setup

Full size image

In this study, a laser machine with a 532-nm green wavelength and an output power of 10 W was used to illuminate the droplets. The laser light was directed through a set of lenses to create a planar light sheet, which was then diverged by a lens with a focal length of -25 mm and converged by a lens with a focal length of 100 mm. This setup was used to produce a laser sheet that could be used to visualize the flow of the droplets. The resulting laser sheet was aligned in parallel with a sapphire glass surface, covering a volume that stretched from the sapphire glass surface to a height of 0.2 mm in the axial direction. A Fastcam Mini camera, equipped with a microscopic lens and a long-pass filter, was positioned parallel to the laser-lit surface and recorded the movement of particles. The long-pass filter is used to block wavelengths shorter than 600 nm while allowing longer wavelengths to pass through. The Fastcam Mini was synchronized with a Fastcam SA5 camera, which captured shadowgraphy images from the side using an IR lamp as a backlight source. An IR long-pass filter (800 nm) was used to eliminate laser reflections and only transmit IR wavelengths. To make the flow visible in the measurements, polymeric fluorescent particles with a diameter of 6 µm were added to the fluid, as shown in Fig. 2. However, it should be noted that the addition of these particles can negatively impact the surface tension and viscosity of the water (Sakai et al. 2007). To ensure that the particles were evenly distributed in the fluid, an ultrasonic cleaner was used before conducting the experiments.

Fig. 2
figure 2

Dark regions in the PIV image

Full size image

To examine the radial velocity distribution of the droplets, spatial averaging over a quarter field was performed. This involved selecting regions of the image that were illuminated more uniformly and extracting the dark regions, as shown in Fig. 2. The goal of this averaging process was to produce a more accurate and representative measurement of the velocity distribution of the droplets by eliminating the influence of noise and other sources of error. The averaging was performed on the discrete data of the droplets according to the following equation:

$$U_{a} \left( {r,\tau } \right) = \frac{2}{\pi }\mathop \int \limits_{{\frac{3\pi }{4}}}^{{\frac{5\pi }{4}}} U\left( {r,\varphi ,\tau } \right)d\varphi$$
(2)

where \(U_{a} \left( {r,\tau } \right)\) is the azimuthally averaged velocity magnitude at the radial position r and at dimensionless time τ. This formula allows for the calculation of the spatial average of the velocity data over a selected region of the image. By performing the averaging in this way, it is possible to obtain a more reliable and accurate measurement of the velocity distribution of the droplets.

In order to obtain high-quality data, it is important to have sufficient lighting and high magnification. Increasing the magnification level can improve the accuracy of the measurements made using PIV, but it also reduces the size of the field of view and the spatial resolution of the data. In this study, the PIV camera was set to magnification values of 3.2 and 6, resulting in image resolutions of 0.0125 mm/pixel and 0.0065 mm/pixel, respectively. These magnification levels allowed for detailed imaging of the droplets as they impacted and spread on the solid surface while still providing sufficient spatial resolution to accurately measure the spreading velocities within the droplets. The impact conditions of droplets were determined by analyzing the pixels of shadowgraph images using ImageJ (Schneider et al. 2012).

From the shadowgraph images before the droplet impact, initial droplet diameter and initial droplet velocity can be obtained by pixel analyzing. In order to enhance the visibility of droplet, background subtraction was applied. The droplet images were then converted to an 8-bit black-and-white format using the Otsu method (Otsu 1979), which is one of the available thresholding options in ImageJ. The fill holes filter was also applied to eliminate the white gaps that are often present inside droplet. However, due to potential processing errors, small objects may sometimes appear in the transformed image, and these can be eliminated by adjusting the minimum object size to only retain the main droplet details.

The equivalent initial droplet diameter can be calculated using the collected data by applying an appropriate formula.

$$D_{0} = 2\sqrt {\frac{Area}{\pi }}$$
(3)

The impact velocity of the droplet can be determined by calculating the rate of change in the vertical position of the center of the droplet between consecutive images and dividing this value by the time difference between the images. 20 000 frames per second (fps) are used to capture the shape changes of the droplets, it means time difference between the images is 0.05. This allows for an accurate determination of the droplet’s velocity upon impact.

$$U_{0} = \frac{{y_{2} - y_{1} }}{\Delta t}$$
(4)

In addition, the values of the constant angles for a droplet on sapphire glass were determined to be 90°, 60°, and 110° for equilibrium, advancing, and receding contact angles, respectively.

In this study, measurements of physical parameters are subject to some level of uncertainty. This uncertainty can be attributed to errors in measuring the droplet diameter and droplet impact velocity. These errors can be further divided into random errors and bias errors. Bias errors, which are typically caused by the measurement instrument itself, cannot be fully eliminated, but they can be minimized through accurate calibration. In image processing, the uncertainty in pixel analysis is approximately 1 pixel, which corresponds to a bias error of approximately 0.02 mm. To quantify the uncertainty in the droplet impact conditions, the random errors can be calculated by analyzing the last few frames (5–10) before each droplet impacts the solid surface. The following equation can be used to determine the random errors of X,

$$S_{X} = \sqrt {\frac{1}{N - 1} \mathop \sum \limits_{i = 1}^{N} \left( {X_{i} - \overline{X}} \right)^{2} }$$
(5)
$$\overline{X} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} X_{i}$$
(6)

The overall uncertainty, which combines both the random and bias uncertainties, can be calculated using the following equation:

$$\delta_{X} = \sqrt {\left( {S_{X} } \right)^{2} + \left( {S_{B,X} } \right)^{2} }$$
(7)

This equation allows us to determine the total uncertainty in a measurement, taking into account both the random errors and the bias errors. The uncertainty in the droplet Weber number can be calculated using the following equation:

$$\frac{{\delta_{We} }}{We} = \sqrt {\left( {\frac{{\delta_{{D_{0} }} }}{{D_{0} }}} \right)^{2} + \left( {2\frac{{\delta_{{U_{0} }} }}{{U_{0} }}} \right)^{2} }$$
(8)

This equation allows us to determine the uncertainty in the Weber number, which is a measure of the relative importance of inertial and surface tension forces on a droplet. For different impact conditions, uncertainty values are given in Table 1.

Table 1 The uncertainty values for different impact conditions
Full size table

3 Results and discussion

As stated in the introduction, many researches have been examined about droplet impingement on solid surface. However, many of these investigations have focused on limited quantitative data, such as the variation of the spreading factor and the height of the lamella. While these parameters are important for understanding droplet behavior, they do not provide a complete picture of the droplet’s motion. By using PIV method, it is possible to obtain not only these limited quantitative data but also a more comprehensive understanding of the droplet’s motion through the measurement of the velocity vector field and average radial velocity profiles in the spreading lamella.

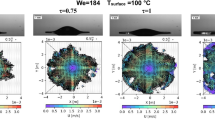
Figure 3 presents qualitative shadowgraph images, velocity vector fields, and radial velocity profiles for a droplet with a Weber number of approximately 5 at ambient temperature at different dimensionless times. Dimensionless time τ is defined as \(\left( {\tau = t\frac{{U_{0} }}{{D_{o} }}} \right)\) where t, \(D_{0}\) and \(U_{0}\) denote physical time, initial droplet diameter, and initial droplet velocity, respectively. During the early spreading process, as seen at a dimensionless time of 0.25, the radial velocity profile is linear. In the middle region of velocity vector field, because of the presence of surface and lateral outflows, a stagnation point develops near the impingement area. As the dimensionless time increases to 0.50, the radial velocity is found to be linear over a comparatively wide range of spreading radius, but due to the influence of capillary and viscous forces, the radial velocity profiles become nonlinear at the exterior radial positions. At a dimensionless time of 0.75, liquid lamella reaches almost maximum spreading diameter value; after that, the liquid lamella begins to recede from the rim toward the center. This can be observed in the velocity vector field, where the velocity vectors at the rim start to change direction. As the dimensionless time increases to 1, the flows from the rim toward the center converge in the center, and the liquid accumulates there, creating an upward flow. This upward flow is caused by the receding of the liquid lamella toward the center as it loses kinetic energy.

Fig. 3
figure 3

a Qualitative shadowgraph images, b velocity vector fields, and c radial velocity profiles for We ≈ 5 case at different dimensionless times. (Droplet diameter is 2.15 mm)

Full size image

The velocity vector fields at ambient temperature for different Weber number cases are presented in Fig. 4 at various dimensionless time values. These vector fields provide information about the movement of the droplets and how they change over time as they impact the solid surface. It is evident from the figures that the spreading behavior of the droplets is influenced by the Weber number. Specifically, for higher Weber cases, the effective spreading area is larger compared to lower Weber cases. This can be attributed to the balance between the impact energy, which drives the droplets outward, and the interfacial energy and viscosity-dissipated energy, which tend to pull the droplets inward. The interplay between these different forces determines the final spreading behavior of the droplets and can be further explored through analysis of the velocity vector fields.

Fig. 4
figure 4

Velocity vector fields for several Weber number cases at different dimensionless times

Full size image

In Fig. 5, the dimensionless radial velocity profiles with dimensionless radius for different Weber number cases at room temperature are displayed at various dimensionless times for all cases. Dimensionless velocity \(\left( {\overline{u} = \frac{U}{{U_{o} }}} \right)\) is obtained by normalizing radial velocity value with respect to the initial droplet velocity, while dimensionless radius \(\left( {\overline{r} = \frac{R}{{D_{0} }}} \right)\) is obtained by normalizing their respective values with respect to the initial droplet diameter. These profiles provide insight into the velocity of the droplets as they spread and recede upon impact with a solid surface. At a dimensionless time of 0.5, the radial velocity profiles for all cases exhibit a similar trend, showing a linear range of spreading radius that becomes nonlinear at the exterior radial positions due to the influence of capillary and viscous forces. This nonlinear behavior is a result of the interplay between the inertial forces driving the droplets outward and the surface tension and viscosity forces pulling the droplets inward. As the dimensionless time increases to 1, the radial velocity profiles for the low and moderate Weber number cases exhibit different trends due to the completion of the spreading process and the onset of the receding process. These trends demonstrate how the Weber number impacts the spreading and receding behavior of the droplets. By analyzing the dimensionless radial velocity profiles, we can gain a better understanding of the mechanisms governing droplet behavior and how these mechanisms change over time.

Fig. 5
figure 5

Dimensionless radial velocity profiles for different Weber number cases at ambient temperature a τ = 0.50 and b τ = 1

Full size image

4 Conclusions

In this study, the impact of radial velocities within droplets on a sapphire glass surface was investigated using PIV and shadowgraph techniques over a wide range of Weber numbers. The results of the study showed that the radial velocity was generally linear throughout a wide range of spreading radius; however, the velocity profiles at the exterior radial positions became nonlinear over time due to the influence of capillary and viscous forces for all cases. This nonlinearity was more pronounced for low Weber numbers, as the viscous forces in the lamella were more significant in comparison to the inertia forces. On the other hand, the radial velocity profile linearity was more apparent for high Weber numbers, as the viscosity effects in the lamella were minor in comparison with the inertia forces. The results also showed that the spreading process was faster for lower Weber numbers, and the receding process began sooner as a result. This was reflected in the different trends observed in the radial velocity profiles for different Weber numbers. Overall, these results demonstrate the complex and dynamic behavior of droplets upon impact with a solid surface and how this behavior changes with the Weber number.