Three-dimensional visualization of columnar vortices in rotating Rayleigh–Bénard convection

Abstract

 To enrich the three-dimensional experimental details of vortex structures in rotating Rayleigh–Bénard convection, we established a technique visualizing three-dimensional vortex structures using scanning planar particle image velocimetry. Experiments were performed at fixed Rayleigh number, $\hbox {Ra} = 1.0 \times 10^7$ and different Taylor numbers from $\hbox {Ta} = 6.0 \times 10^6$ to $1.0 \times 10^8$, corresponding to convective Rossby numbers from $0.1 \le \hbox {Ro} \le 0.5$ at which gradual transition between vortical plumes and convective Taylor columns regime is observed. Stream function distributions calculated from horizontal velocity vector fields visualize the vortex structure formed in the regimes. As quantitative information extracted from the visualized structures, distances between vortices recognized on the distributions show a good agreement with that evaluated by a theory. With the accumulated planar stream function distributions and vertical velocity component calculated from the horizontal velocity vectors, the three-dimensional representations of vortices indicate that quasi-two-dimensional columnar vortices straighten in the vertical direction with increasing Ta.

Graphic abstract

1 Introduction

Rayleigh–Bénard convection (RBC), a natural convection induced by a vertical temperature gradient in a fluid layer, is one of the basic configurations arising in physics and engineering problems on heat transfer. In addition, the confinement of the fluid motion by applying a background rotation in RBCs provides significant opportunities to understand geophysical fluid motion, as, for example, the motion in Earth’s outer-core.

RBC is governed by the Rayleigh number—$\hbox {Ra} = g\beta \varDelta T H^3/(\kappa \nu )$, Prandtl number—$\hbox {Pr} = \nu / \kappa$, and parameter values of the vessel’s shapes including its aspect ratio. Here, g, H, and $\varDelta T$ are the acceleration of gravity, height of the fluid layer, and the vertical temperature difference, respectively; $\beta$, $\nu$, and $\kappa$ are the thermal expansion coefficient, the kinematic viscosity, and the thermal diffusivity of the fluids involved, respectively. The influence of the background rotation is determined by the Taylor number, $\hbox {Ta} = (2\varOmega H^2/\nu )^2$, where $\varOmega$ is the background rotation rate; in representing the relative influence from buoyancy, the (convective) Rossby number, $\hbox {Ro} = [\hbox {Ra}/(\hbox {PrTa}) ]^{1/2} = (g\beta \varDelta T/H)^{1/2}/(2\varOmega )$, has been used. Recent studies have indicated that there are four regimes along decreasing Ro values in sufficiently large Ra conditions with $\hbox {Pr} > 0.2$, namely (rotation-affected) thermal turbulence, vortical plumes, convective Taylor columns (CTCs), and cellular regimes identified by the Nusselt number (Nu) variations and visualization of vortical structures (Liu and Ecke 2009; Weiss and Ahlers 2011; Julien et al. 2012; Stevens et al. 2013). Review of these recent experimental works performed in the vessels with different aspect ratios by Cheng et al. (2018) provides summary of the regime transitions and limitations of parameter ranges which we can explore.

Most interests of the past experimental studies were for investigating power law of Nu variations through the regimes especially for rapidly rotating RBC ($\hbox {Ro} \ll 1$). Some works, however, provided efforts on understanding vortex structures and its motions that dominate the Nu variations, and also local and instantaneous heat transfer characteristics. Cheng et al. (2015) performed flow visualizations of the structures in each regime using flake particles. Kunnen et al. (2008) investigated the breakdown of the large-scale circulation using stereoscopic particle image velocimetry (PIV) and its influence on heat transfer. Vorobieff and Ecke (2002) represented development of structures with Ro as streamline patterns taken by PIV. Rajaei et al. (2017) represented the structures by spatial autocorrelation of vorticity measured by planar PIV. Sakai (1997) visualized temperature field of quasi-two-dimensional columnar vortices using encapsulated thermochromic liquid crystals (TLCs) to confirm the theory for describing stable distance of neighboring vortices. Our group also performed temperature field measurement using TLCs in a fluid layer with a relatively large aspect ratio, and quantified motion of columnar vortices in different time scales (Noto et al. 2018, 2019).

In the gradual transition from vortical plumes to CTCs regimes, vortices increase two-dimensionality. Noto et al. (2019) quantified it as vertical deviation of vertical velocity component measured by PIV on a vertical cross section of a fluid layer. Numerical simulations summarized in Stellmach et al. (2014) also explained that CTCs have “sheath” of different signs of vorticity and prevent interaction with neighboring vortices. Rajaei et al. (2017) represented three-dimensional (3D) shape of the vortices in the different regimes by Q-criterion method with 3D particle tracking velocimetry (3D PTV). Visualized vortex structures, however, are restricted in a small domain obeying the limitation of 3D PTV due to requirement for overlap of focal range of multiple cameras. A classical planar PIV can visualize 2D slices of the vortex structures in wider domains. In addition, a simple methodology based on the planar PIV to capture the 3D character of the vortex structures is efficient to detail quasi-2D or 3D vortex structure in wider domain. For the 3D vortex structures in the CTCs and vortical plumes regimes, this study provides such details by developing a simple visualization technique of the vortex structures based on velocity field data obtained using scanning planar PIV, which is conventional technique with scanning illumination by movable laser sheet (e.g., Ushijima and Tanaka 1996), considering sufficiently slow advection of the columnar vortices, and post-processing.

The structure of this paper is as follows: Details of the experimental setup and scanning PIV system are explained in Sect. 2. The applicability of the scanning PIV and post-processing are summarized in Sect. 3. The 3D vortex structure and its development with increasing Ta are analyzed from global and local perspectives in Sect. 4. Finally, concluding remarks of this study are presented in Sect. 5.

2 Experimental setup and measurements

2.1 Experimental setup

Details of the setup for rotating RBC experiment were given in our previous papers Noto et al. (2018, 2019). Here, we summarize important points from them.

The experiments were conducted on a turntable (Fig. 1), on which a rectangular fluid vessel with dimensions $200 \times 200$ $\hbox {mm}^2$ horizontally and height $H = 40$ mm (aspect ratio $\varGamma = 5$), an automatic elevation system, and an optical measurement system are arranged as the main components of the setup. The working fluid was distilled water containing porous resin particles of specific gravity 1.01 and diameter 63 – 75 $\upmu$m. The vessel has side walls of 10-mm-thick transparent acrylic having sufficiently high thermal insulation, a top plate of 3-mm-thick transparent glass for visualization, and a bottom plate of 10-mm-tick copper sheeting. The vessel is centered on the rotation axis of the turntable. The top- and bottom-plate temperatures were maintained, respectively, by circulating cool water from a thermostatic bath and by a silicone rubber heater embedded in the bottom plate. Temperature differences in the fluid layer for the estimation of Ra value were given from the monitored values in the copper plate and a reference point beneath the glass plate.

Fig. 1

Schematic overview of the experimental systems on the rotating table; 1 high-speed camera, 2 laser sheet with automated elevator (only for scanning PIV), 3 glass plate, 4 cooling water from thermostat bath, 5 rectangular fluid layer ($200 \times 200 \times 40$ $\hbox {mm}^3$), 6 acrylic wall, 7 copper plate with a heater inside, 8 turntable

The turntable is a two-stage table with a round stainless plate of diameter 1 m and is rotated by an AC servo motor via a belt with a set constant speed within 0.01% of fluctuations. Base frames of the table are fixed to the floor by anchor bolts for stable rotation; thus, the levelness of the stages can be kept within 0.05$^\circ$. Using a rotary joint connected to the shaft of table allows cooling water and electricity supply to the table from exterior. The upper table has a hole of diameter 0.2 m at the center through which a video camera images the fluid layer near the center of the bottom table. To obtain the horizontal velocity field in PIV, a horizontal plane was illuminated by a laser light sheet with around 1-mm-thickness created using a 2-W continuous laser source (wavelength 532 nm) and a cylindrical lens through the transparent side walls. The laser sheet has to be moved in the vertical direction without manual operation to capture scanning images on the turntable. The lens and the head of an optical fiber cable connected with the laser source were mounted on an automated elevator installed on the turntable. The elevator includes an actuator, devices for controlling the actuator, the holder of the light source, and so on. This elevator system is set on the turntable and controlled by software (LabVIEW) installed on a PC. A high-speed video camera (Optronis, GmbH, CR600x2, $1280\times 1024$ pixels in the full resolution) was used to capture sequential particle images in the fluid layer with 50 f.p.s as the frame rate (1/50 s as the shutter speed). The camera was rotated together with the turntable and its optical axis coincides with the rotation axis of the turntable. Taking images for scanning PIV using a fixed camera and moving laser sheet can be performed by setting the depth of field of the camera at appropriate values for a wide range of focal lengths (45.07 mm in the estimated depth of field with 2.8 in F-number of the lens).

Additionally, we conducted supplementary experiments to measure flow field on a vertical cross section for checking the validity of the estimation of vertical stream noted in Sect. 4.1 by a direct measurement of the vertical flow using simple planar PIV with direct cross-correlation algorithm. The collected sets of experimental parameters, non-dimensional numbers, and conditions are listed in Table 1.

Table 1 Conditions and parameters for each run of the experiment: Condition No. 5 was conducted to analyze the advection velocity of a vortex for a comparison with lift speed

2.2 Scanning PIV system

We assume fully developed vortical structures for measurements in visualizing the typical vortex structures. Zhong et al. (1993) specified the time series of the flow fields from early stages of the rotating convection to fully developed state. In this study, we had 30 min preparation time that is long enough for reaching the fully developed state; statistically settled structures were observed after that preparation time in our previous study (Noto et al. 2019). The parameter values used in PIV analysis of the field images are adjusted to obtain a sufficient number of velocity vector grids to capture the vortex shape. Size of images corresponding to the entire fluid layer equivalent to $200 \times 200$ $\hbox {mm}^2$ changes depending on the height of horizontal layers illuminated in the scanning system explained below. The number of the horizontal grid at the half height is $188 \times 188$; the grids are arranged over the $945 \times 945$ pixels image. The side boundaries of the vector field correspond to the side walls of fluid layer. Corresponding spatial resolution, interval of regular grid in PIV analysis, is around 0.2 mm and is small enough to resolve expected size of vortices, 10 mm in the smallest case, at $\hbox {Ta} = 1.0 \times 10^8$. Examples of a path line representing the actual flow field qualitatively and the corresponding vector field are shown in Fig. 2. The path lines represent some vortices in the fluid layer, and the velocity vector field obtained from PIV indicates the presence of vortices at the corresponding positions.

Sequential images were taken by the video camera. As the laser sheet in the scanning system is moved continuously, there is a difference in height in the fluid layer between two successive images for PIV analysis with direct cross-correlation algorithm providing an instantaneous velocity vector field in the horizontal plane. The difference in height will be negligibly small relative to the thickness of the laser sheet if the rate of rise of the laser sheet is slow enough in comparison with the recording speed of the images. Also, low rising rates relative to the advection speed of vortices cannot provide quasi-instantaneous vortex structure. In contrast, high-speed recording provides insufficient particle displacements between two successive images and causes measurement error. A trade-off is required in setting a value, which we determined 5 mm/s. This is much faster than the advection speed of the quasi-columnar vortices, around 0.2 mm/s evaluated in this experiment at the highest Ta numbers we examined by standard planar PIV measurements (No. 5 in Table 1) and also from previous study detected from temperature fields (Noto et al. 2019). The 40-mm fluid layer is, therefore, divided into 80 scanning layers corresponding to a resolution of 0.5 mm. During scanning, the sheet rises from the bottom to the top of fluid layer in 8 s and returns in 2 s. This cycle is repeated six times to capture images. In the single scanning, vortices potentially move in 1.6 mm that is estimated from the maximum advection speed of vortices mentioned above. This displacement is comparable to two-PIV-grid spacing, and any difference within this scale should be disregarded in discussions. As references, time scales calculated from Prandtl’s free fall velocity and the rotation rate of the turntable at the highest Ta case are $\sqrt{H/(g\beta \varDelta T)} = 1.34$ s and $2\pi /\varOmega = 2$ s, respectively.

A set of the velocity vector fields obtained is given in Fig. 3a–c; the sides of the square vector field equal 1.1H. Panels (a) and (c) show similar patterns of vortices with opposite rotation direction because of the symmetry with respect to the mid-plane. In contrast to this, the velocity field at the mid-plane of the fluid layer (Fig. 3b) has a different flow pattern with a weak horizontal stream (see also supplemental movie for sequential velocity vector fields along scanning: scan_piv.avi). Experiments were performed at a fixed Rayleigh number, $\hbox {Ra} = 1.0 \times 10^7$ with Taylor number varying from $\hbox {Ta} = 6.0 \times 10^6$ to $1.0 \times 10^8$. Thermal turbulence emerges at this Ra condition, while sufficiently fast background rotations, e.g., sufficiently large Ta conditions, suppress the turbulence. Then, the flows are restricted into quasi-two-dimensional (quasi-2D) forms, where the vertical variation of the flow without the top and bottom Ekman layer is suppressed according to Taylor–Proudman theorem; the convection reaches 2D state at sufficiently small Ro numbers in ideal situations (e.g., Greenspan 1968). This parameter range examined here lies on vortical plumes and CTCs regimes distinguished as quasi-2D states (Noto et al. 2019).

Fig. 2

Examples of a flow field visualized by particle path line and b vector field calculated from two successive images; five images were taken in 1 s to form the path line ($\hbox {Ra} = 1.0 \times 10^7$, $\hbox {Ta} = 1.0 \times 10^8$ and $z \sim 0.1H$)

3 Visualization of vortices in the 3D domain

3.1 Visualization of vortices by stream function

Vorticity distributions are usually used to visualize vortical structures, and in rotating convections, there have been several demonstrations based on results of numerical simulations representing this structure using vorticity (Vorobieff and Ecke 2002; Julien et al. 1996). The vertical component of vorticity is calculated from $\omega _z = \partial v/\partial x - \partial u/\partial y$. In experimental studies, however, there are difficulties in doing this because measurement errors propagate when estimating differential quantities in numerical differentials. Examples of the vorticity distribution are shown in Fig. 3d–f, where $\omega _z$ in each distribution was calculated from the velocity vectors shown in Fig. 3a–c along the equation above. Color contours of the distributions fluctuated discontinuously and shape of vortices are hard to be imagined from the distributions. We therefore consider to approximate the vortex structures using the stream function distribution, an integral quantity that may avoid augmenting the measurement errors. The stream function is used in expressing analytically the 2D flow of an incompressible fluid. The contours of the stream function represent stream lines, and closed contours of positive and negative values identify cyclonic and anti-cyclonic vortices. The stream function $\varPsi$ is defined as $u = \partial \varPsi /\partial y$, $v = -\partial \varPsi /\partial x$. Our previous study on Taylor-Couette flow also adopted stream function to visualize Taylor vortices which are toroidal vortices formed in a gap between co-axial cylinders (Watamura et al. 2013).

Fig. 3

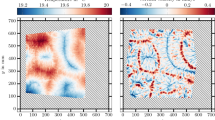
Examples of horizontal velocity vector fields (a–c), z-component of vorticity (d–f), stream functions (g–i), and vertical velocity components (j–l) in a section of size $1.1H \times 1.1H$ extracted from the field obtained from scanning PIV at $\hbox {Ra} = 1.0 \times 10^7$, $\hbox {Ta} = 1.0 \times 10^8$ (experimental condition No. 4 in Table 1). The corresponding height of the planes in the fluid layer is (top) $z = 0.75H$, (middle) $z = 0.5H$ and (bottom) 0.25H. White and black dots on the stream function distribution mark vortex centers determined in template matching

There are various methods to calculate the stream function from planar PIV data, u(x, y), and v(x, y), and here, we adopt the Poisson equation to obtain smooth distribution for the stream function despite the presence of measurement noise in the PIV data. Substituting the equations for stream function into the equation of $\omega _z$ mentioned above yields the Poisson equation for the stream function,

$$\begin{aligned} \frac{\partial ^2 \varPsi }{\partial x^2} + \frac{\partial ^2 \varPsi }{\partial y^2} = -\,\omega _z. \end{aligned}$$

(1)

The Gauss–Seidel method was used to solve this Poisson equation with following difference equation on preliminary calculated vertical vorticity component $\omega _z$ from PIV data:

$$\begin{aligned} \varPsi _{i,j} = \frac{\varPsi _{i+1,j}+\varPsi _{i-1,j}+\varPsi _{i,j+1}+\varPsi _{i,j-1}}{4} + \frac{1}{4}\varDelta ^2 \omega _{z, i, j}, \end{aligned}$$

(2)

where i and j denote grid index for the x and y axes, and $\varDelta$ is the common grid distance in x and y directions of the PIV data. Here, we set $\varPsi = 0$ as the initial condition, and $\varPsi = 0$ on the side walls was also given as boundary conditions in sequential calculations of $\varPsi _{i,j}$ in Eq. (2). Iterations of the Gauss–Seidel method provide smooth stream lines describing 3D vortex field. The original velocity vector fields shown in Fig. 2b as an example contain measurement errors and the numerical integration of Eq. (1) is accompanied by the accumulation of errors. To detrend, we calculated the local average of the stream function for $10 \times 10$ grids and subtracted it from the original values of the stream function.

An example of the stream function after detrending is shown in Fig. 4, where the stream function is normalized by an averaged absolute value of local maximums/minimums of the stream function in the 3D domain for better visibility. (We will perform this normalization for all results hereafter.) PIV data for the calculation were obtained at $\hbox {Ra} = 1.0 \times 10^7$ and $\hbox {Ta} = 1.0 \times 10^8$. Here, the left figure shows the horizontal distribution obtained from the stream function at $z = 0.25H$ over the entire fluid layer, where the sides of the figure correspond to the side walls of fluid vessel. Positive and negative values of the stream function indicate clockwise (cyclonic) and counterclockwise (anti-cyclonic) vortices. Both vortices seem to distribute uniformly over the entire horizontal fluid layer. The right figure shows a vertical stream function field constructed with the accumulation of 80 horizontal distributions obtained by scanning. The extracted horizontal position is indicated by a black broken line in the left figure. Vortices visualized by the stream function in the horizontal plane seem to have qualitative agreement with Sakai’s visualized temperature field (Sakai 1997). In contrast, in the vertical distribution, vortices represented by the stream function distribution are tilted in the vertical direction unlike Sakai’s visualization, where the isothermal column of each vortex appears straight in the vertical direction. This is because direction of rotation of the vortices switches to the opposite one at the horizontal mid-plane. Details of vortex morphology visualized by different physical values will be mentioned in Sect. 4.2. Combining scanning PIV data and the visualization from the stream function distribution allows us to reconstruct the 3D vortex structure over the entire fluid layer. Figure 5 shows the isosurface of the stream function constructed from the same scanning field shown in Fig. 4; red and blue indicate positive and negative fixed values of the stream function. The boundaries of the fluid layer are marked by the black frame. Details of the 3D structure are discussed in Sect. 4.2.

We return to Fig. 3 to compare the vortices visualized using the stream function distribution with those from the original velocity vectors. The stream function distributions shown in panels (g)–(i) were calculated from the velocity vectors shown in panels (a)–(c) via the vorticity distributions shown in panels (d)–(f) at different heights of the fluid layer. For both cyclonic and anti-cyclonic vortices, the positions and rotational directions of the vortices agree. In addition, the distributions of stream function provide much smooth representation of the vortices than the distributions of vorticity. The relation between vorticity and stream function distributions involves second-order derivative; hence, the shape of the vortices visualized by these two different quantities will be different. Nevertheless, around the vortex centers, the stream function takes on a Gaussian-like distribution (to be discussed in the next section). The outline and size of vortices therefore do not change very much between the two expressions.

Fig. 4

Example of stream function distributions calculated from the velocity vector field measured in scanning PIV at $\hbox {Ra} = 1.0 \times 10^7$ and $\hbox {Ta} = 1.0 \times 10^8$; (left) a horizontal distribution of stream function at $z = 0.25H$ in the entire fluid layer, where each side corresponds to the side walls of the fluid layer; (right) a vertical stream function field constructed by accumulation of 80 horizontal distributions of the stream function obtained by scanning. Black broken lines in each figure indicate height and depth of the extracted horizontal and vertical cross sections

Fig. 5

Example of a 3D vortex distribution represented as isosurface of stream function: Red and blue isosurfaces indicate positive and negative fixed values, associated with the cyclonic and anti-cyclonic vortices. Black frame marks the edges of the fluid layer. Values for the isosurfaces were determined by considering the visibility of the vortices. Base PIV data for the isosurface were obtained at $\hbox {Ra} = 1.0 \times 10^7$ and $\hbox {Ta} = 1.0 \times 10^8$

3.2 Horizontal scale of vortices

For validation of the visualization methodology using stream function, the horizontal scale of the vortices, which is one of the characteristic values in rotating RBCs, particularly those in the regime satisfying the condition to form quasi-2D columnar vortices, is evaluated and compared with previous results. The horizontal scale is measured through two steps: vortex center identification and the calculation of the corresponding Voronoi polygons of the vortices. Vortex centers are identified from the stream function distribution using the mask correlation method, which is a standard method used in finding a certain pattern in images (Takehara and Etoh 1999). A Gaussian distribution template

$$\begin{aligned} f(x, y) = \exp \left[ -\frac{(x-x_0)^2 + (y-y_0)^2}{2\sigma ^2} \right] , \end{aligned}$$

(3)

is used as a vortex pattern for the stream function. Here, $\sigma$ is the fitted variance value of the distribution and is a length having half the size of the characteristic mask diameter (Takehara and Etoh 1999). The template size of the Gaussian distribution is chosen as the expected horizontal size of the vortices (to be discussed later). The template, as shown in Eq. (3), is swept to the stream function distributions by changing the center of the template pattern, $(x_0, y_0)$, and taking cross-correlation with the stream function value, C(x, y). Center positions are determined as positions having the larger value of the cross-correlation than the setting threshold, $|C| > 0.5$. In cases when multiple center positions are detected those are shorter than $\sigma$, the center positions having a smaller correlation value are eliminated. Negative cross-correlation values indicate anti-cyclonic vortices. The results of the vortex center detection are shown in Fig. 3g–i. These are extracted stream function distribution for a $1.1H \times 1.1H$ square cross section at each height of the fluid layer; white and black dots mark the centers of the cyclonic and anti-cyclonic vortices.

A Voronoi drawing is one method of partitioning an image plane with dispersed dots into regions surrounding each dot. This method is adopted to evaluate the size of vortices. Here, each boundary of a region corresponds to a bisector of a pair of neighboring dots; the bisectors trace out a polygon. There are examples of the application of the Voronoi drawing to identify boundaries of convection cells in RBCs without background rotation and Bénard-Marangoni convection (Trouette et al. 2011; Mazzoni et al. 2008; Cerisier et al. 1987). An example of a Voronoi polygons obtained from a present setting is shown in Fig. 6. Apices of the Voronoi polygons are arranged around the vortex centers indicated by black on white dots; the Voronoi polygons appear to provide a reasonable approximation of the area of the individual vortices. Assuming that each Voronoi polygon approximates the area of the corresponding vortex, S, the horizontal scale of the vortices can be taken as the equivalent circle diameter, $L_{\mathrm {exp}}$. The calculation takes an average of all S and thereby yields the averaged horizontal scale of the vortices, i.e., ${\overline{L}}_{\mathrm {exp}}=2({\overline{S}}/\pi )^{1/2}$, where the over-line indicates the averaged value.

Fig. 6

Voronoi drawing of a stream function distribution with square area of 1.25H in sides and conceptual diagram of a Voronoi polygon and equivalent circle, where dots on the stream function distribution mark the centers of the vortices determined by template matching

In evaluating the estimated value of the horizontal scale of vortices, a theoretical formula proposed by Sakai (1997) is used. The formula is

$$\begin{aligned} L_{\mathrm {th}} = 4.6H \frac{\delta _{\mathrm {t}}^2}{2\delta _{\mathrm {t}}^2 + 2\delta _{\mathrm {t}} \delta _{\mathrm {E}} +\delta _{\mathrm {E}}^2} \hbox {Ra}^{1/3}\hbox {Ta}^{-3/8}, \end{aligned}$$

(4)

where $\delta _\mathrm {t}$ and $\delta _{\mathrm {E}}$ are the thicknesses of the thermal boundary layer and the Ekman layer, respectively, with estimates $\delta _{\mathrm {t}} = 3.8 H \hbox {Ra}^{-1/3}$ and $\delta _{\mathrm {E}} = \sqrt{2}H \hbox {Ta}^{-1/4}$. A comparison of the estimated results of the horizontal scale obtained experimentally and theoretically from Eq. (4) is given in Fig. 7. Here, the experimental results are from four different Ro (or Ta) values, namely $\hbox {Ro} = 0.50$, 0.37, 0.15, and 0.12 (corresponding to $\hbox {Ta} = 6.0 \times 10^6$, $1.0 \times 10^7$, $6.0 \times 10^7$ and $1.0 \times 10^8$) obtained at two different heights of the fluid layer, $z = 0.25H$ and 0.75H. The solid line in the figure represents the correspondence with theoretical estimates from Eq. (4); proximity to the line indicates the degree of agreement. For all the set parameters and heights, the present experimental results show good agreement with the theoretical estimates, $R^2 = 0.94$ in the determination coefficient. Further, the present results have a much smaller deviation from the theoretical values than the experimental results from Sakai (1997) indicated by plus signs. We therefore conclude that the representation of vortices using the stream function has sufficient applicability in rotating RBCs at least for the parameter range investigated.

Fig. 7

Horizontal scale of vortices obtained experimentally for different parameter settings versus the theoretical estimates from Eq. (4), normalized by height of the fluid layer; crosses correspond to data from Sakai (1997)

4 Details of the 3D structure of vortices

4.1 Estimation of vertical stream through the vortices

We have evaluated the visualization technique of vortical structure in a horizontal plane using stream function calculated from the 2D velocity vector field measured from PIV. The 3D vortex structures are represented by accumulating 80 layers of the stream function distribution captured by the scanning system (Fig. 5). There are vertical streams caused by the Ekman pumping generated by a vertical pressure gradient through the quasi-2D vortices in the Ekman layer in the top and bottom boundaries of the fluid layer: These streams dominate heat transfer between these boundaries in this regime (Stevens et al. 2013). Here, we evaluate the 3D vortex structure taking into account vertical stream.

Scanning PIV enables to obtain the 2D velocity vector fields at each height of the fluid layer. This series of velocity vector fields forms quasi-instantaneous 3D vector field of two-component velocities over the entire fluid layer. The out-of-plane component of velocity, that is, the vertical velocity w, is then calculated via the equation of continuity for incompressible fluids with boundary conditions, specifically, the non-slip condition at the top, the bottom, and the side boundaries. That is,

$$\begin{aligned} w(x,y,z) = -\int _0^z \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) \hbox {d}z. \end{aligned}$$

(5)

A simple numerical integration of the equation above over the multiple scanning layers was performed. The thickness of the Ekman boundary layer is estimated as $\delta _{\mathrm {E}} = \sqrt{2}H\hbox {Ta}^{-1/4} = O$(0.1 mm) in the present cases, which is comparable to the thickness of the scanning layer of around 0.5 mm. The calculated vertical velocity component, therefore, is potentially underestimated in comparison with the original value.

Examples of horizontal fields of the vertical velocity component calculated from the horizontal velocity vector fields on the same sections (Fig. 3a–c) are shown in Fig. 3j–l at each height of the fluid layer for parameter setting $\hbox {Ra} = 1.0 \times 10^7$ and $\hbox {Ta} = 1.0 \times 10^8$; red and blue areas indicate upward and downward flows. The contour of w in the figure is less smooth, unlike the stream function distribution shown in Fig. 3g–i, because the calculation of w contains numerical derivations in u and v and augments the measurement error in the 2D velocity vector field measured from planar PIV. There is a similarity between the vertical velocity distributions and vortex flows indicating horizontal velocity fields and stream functions. In addition, there are strong vertical flows—upward, and downward flows—near vortex centers. Each vertical flow has the same direction at each position of the vertical axis regardless of the rotational direction of the vortex. The local maxima of the vertical stream around the vortex centers are about $|w| = 2$ mm/s, and this value agrees well with results of PIV measurement on a vertical cross section performed in an independent series of supplementary experiments with the same parameter settings. Figure 8 provides comparison of vertical velocity distributions on a vertical cross section obtained using the present calculation method (Fig. 8a) and the direct measurement using planar PIV (Fig. 8b) at $\hbox {Ta} = 6.0 \times 10^7$, where the color range for the velocity contours is set narrower than the maximum values to see the vertical stream structures clearly. For providing fair comparison, the velocity distribution in Fig. 8b is time average in 8 s corresponding to the duration of lift movement for the scanning. As mentioned above, the velocities obtained from the different measurements and the representation of the vertical stream structure look similar despite differences in the fine structure resulting from the difference in measurements.

Fig. 8

Comparison of the vertical velocity distributions on a vertical cross section obtained by a horizontal velocity vector fields from the equation of continuity and b direct measurement from PIV at $\hbox {Ta} = 6.0 \times 10^7$ (experimental condition No. 6 in Table 1), where the latter velocity field is time-averaged in 8 s corresponding to the duration of lift movement

4.2 3D structure of neighboring vortices

With the quasi-instantaneous, 3D velocity vector fields, and the stream function fields for the entire fluid layer, we next discuss the 3D vortex structures. It is especially for local flow structures, and its dependence on Taylor number extracted from the isosurface of the quantities representing quasi-2D columnar vortices.

In Fig. 9, the flow field for a single pair of quasi-2D columnar vortices is represented as (a) isosurfaces of the stream function, (b) a vortex center distribution, and (c) isosurfaces of the vertical velocity component in a domain of dimension $0.4H \times 0.5H \times H$ from two different viewpoints. In panels (a) and (b), red indicates data referring to cyclonic vortices; blue to anti-cyclonic vortices. In Fig. 9c, red and blue signify upward and downward flows, respectively. In the domain, the cyclonic and anti-cyclonic vortices extend from the top and bottom boundaries of the fluid layer, skew at mid-plane and thereafter follow a straight path toward the opposite boundary. The vortices of the pair rush each other at mid-plane without disappearing. The profile of the vortex center (Fig. 9b) supports this feature of the vortex deformation. In contrast, the isosurface of each vertical velocity component stands vertically without skewing throughout the columnar vortices. Despite the different rotation directions of the vortices and their vertical skewing around each other, the vertical streams remain straight and consequently connect the Ekman boundary layers of the top and bottom walls, where the vortices are generated. This structure features a spiral trajectory predicted by Veronis (1959) for rotating convection with considering the motion of fluid particles.

Fig. 9

Vortex structure and vertical stream from two different view points depicted by a isosurfaces of the stream function, b the distribution of vortex centers and c isosurfaces of the vertical velocity w; red and blue signify cyclonic and anti-cyclonic vortices in a, b, while upward and downward flows in c; the domain of the display box (black frame) is $0.4H \times 0.5H \times H$. Parameter settings for the measurement of the original velocity vector field are $\hbox {Ra} = 1.0 \times 10^7$ and $\hbox {Ta} = 1.0 \times 10^7$. The structures observed from different viewpoints are available in supplemental movies (sf_3d_3.avi, w_3d_3.avi)

The same representation of the 3D vortex structure is given for a wider domain, $0.9H \times 0.9H \times H$, in Fig. 10 at two different Taylor numbers, (a) $\hbox {Ta} = 6.0 \times 10^6$ and (b) $1.0 \times 10^8$, to investigate development of the vortex structure with Ta. As mentioned in Sect. 3.2, the horizontal scale of the vortices decreases with increasing Ta, and the change in the vortex thickness in the figures seems reasonable based on this fact. The 3D vortex structures seen from different view points in the figure contain entangled cyclonic and anti-cyclonic vortices for both Ta values. However, the quasi-2D columnar vortices for higher Ta seem straighter except at mid-plane of the fluid layer, where vortices twist around each other. This feature is also evident in the vertical distributions of the stream function and the vertical velocity component (Fig. 11); the quasi-2D columnar vortices become narrower and straighter at higher Ta than lower Ta. This transition on vortex morphology is significant in comparison with pseudo-distortion of vortices caused by advection of vortices during image scanning in the vertical direction. This represents gradual transition from vortical plume to CTCs regimes, namely the vortices increase their two-dimensionality in the vertical direction. Such 2D confinement may be related to enhancement of the heat transfer rate of the fluid layer with increasing Ta (e.g., Liu and Ecke 2009; Stevens et al. 2009, 2011, 2013; Stellmach et al. 2014).

Fig. 10

Development of the 3D vortex structure represented by the isosurface of the stream function obtained at different Ta numbers, a$\hbox {Ta} = 6.0 \times 10^6$ and b$1.0 \times 10^8$, from three different viewpoints; red and blue signify cyclonic and anti-cyclonic vortices. The domain (black frame) is $0.9H \times 0.9H \times H$. The structures observed from other viewpoints are available in supplemental movies (rep755.avi for a and rep3100.avi for b)

Fig. 11

Development of a 3D vortex structure extracted at $y = 30$ mm and obtained at different Ta numbers a$\hbox {Ta} = 6.0 \times 10^6$ and b$1.0 \times 10^8$ as represented by vertical cross sections of the stream function (top) and vertical velocity component (bottom)

5 Concluding remarks

We established a simple visualization technique for columnar vortex structures of rotating RBCs in 3D domain based on velocity field information. The explored range of parameters of Ra and Ta corresponds to the gradual transition between vortical plume and convective Taylor columns regime. Stream function distributions calculated from 2D velocity vectors measured by simple scanning planar PIV provide representation of the vortex structures, where using stream function instead of vorticity can avoid augment of measurement noise by numerical derivative on the discrete velocity data. The distance between vortices estimated from the distribution agreed well with theoretical estimations. The vertical velocity components were calculated from the horizontal velocity vector field at sequential heights in the fluid layer through the equation of continuity and showed good agreement with direct measurement of the vertical velocity component achieved from PIV on a vertical plane. The 3D representations of the vortices by accumulating planar information of the stream function show shape of columnar vortices in transition between the regimes, and these with vertical velocity components suggested that quasi-2D columnar vortices are straightened by increasing the Ta value toward 2D convection. The present methodology is applicable to represent temporal variation of the vortex structure thanks to the sufficiently faster scanning of the layers than advection timescale of the vortices.