Saddle point of separation/attachment and topology transition in laminar juncture flows

Abstract

Laminar juncture flow is numerically studied to investigate the outermost saddle point of separation/attachment (S_S/S_A) and the topological transition. The topological transition trends obtained through computational results are in close agreement with the experiments. The outermost topology in the symmetry plane tends to transform from attachment to separation as the obstacle shape bluntness increases or as the ratio of the boundary layer thickness to the maximum width of the obstacle δ/W decreases. A coefficient C_S/A based on Lighthill’s volume flow theory is devised to estimate the separation or attachment of the fluid. The newly proposed criterion is applied to the limiting streamlines, very close to the flat surface, in the vicinity of saddle point to decide its topological nature. A single quadrant around the saddle point is considered for detailed theoretical analysis, and its further division into four subzones facilitates the application of the proposed criterion (C_S/A) to assess the flow attachment and separation characteristics. The decisive coefficient is successfully applied at various locations with separation/attachment flow configurations and found consistent with the qualitative results.

Graphical Abstract

1 Introduction

Juncture flows (Simpson 2001) exist in various engineering applications, such as airplane’s wing-body junction, the bases of compressor cascade, bridge pier-riverbed junction, in the junctions of heat exchanger, etc. A horseshoe vortex (HSV) system arises as an incoming boundary layer on a plate surface (surface hereafter) confronts an adverse pressure gradient induced by an obstacle mounted on the surface. Besides its broad engineering application, juncture flow has attracted the attention of many researchers because of its richness in three-dimensional (3-D) flow separation and dynamic vortex systems. Therefore, juncture flow offers good prospects for further investigating the classical 3-D flow separation problem. The relationship between skin-friction (or footprint) topology (Zhong et al. 2015) and spatial flow structure is one of significance research area which needs further elaboration.

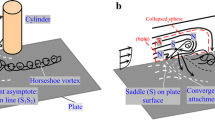
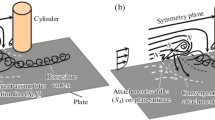
In 3-D juncture flows, as shown in Fig. 1a (Zhang et al. 2012a), the most upstream singular point on the surface, usually exhibits a saddle point (S) in oil flow visualization experiment. The saddle point is conventionally called the separation saddle point (S_S) (Zhang et al. 2012a) and the convergent asymptote (S₁S₂) of skin-friction lines issues from the saddle point is conventionally described as the separation line. The vortex sheet, originating from S₁S₂ and S, is usually treated as the separation surface. In the vertical symmetry plane (plane hereafter), the outermost topology is a separation half saddle point (S′) and the fluid on both sides of the singularity and the separation surface separates from the surface and rolls into the HSV system. This 3-D steady separation topology has been well accepted and is frequently applied in the analysis of 3-D steady flow separation (Le Clainche et al. 2016; Rodriguez and Theofilis 2010; Le Clainche et al. 2015).

Fig. 1

Schematics for the juncture flow topology with saddle point of a separation and b attachment (Zhang et al. 2012a)

In the past, the attachment saddle point (S_A) [Fig. 1b (Zhang et al. 2012a)] has not attracted sufficient attention from researchers (Chapman 1986). Apparently on the surface, the topology is also a saddle (just like separation) and the skin-friction line issues from the saddle is also a convergent asymptote, but in 3-D space the fluids near the singularity attach to the surface and the outermost topology in the symmetry plane is a half node point (N′) emitted from a spatial saddle point (S). The approaching upstream fluid out of the symmetrical plane turns downward and attaches to the plate surface when it reaches the spatial black dash line originated from the spatial S. Both of the two patterns in the symmetric planes (Fig. 1a, b) satisfy the topological constraints (Hunt et al. 1978; Foss 2004; Liu et al. 2011). Researchers usually simplify the attachment as the inverse of separation. However, the S_A (fluid attaches to the surface saddle) should not only be treated as the converse of the S_S (fluid separates from the surface saddle) but it is of great significance in the establishment of separation/attachment criteria.

The pattern of the surface saddle (separation or attachment) implies that the flow separation occurs from the plate surface or spatial shear layer (Fig. 1), which indicates that the vorticity of the vortex system (HSV here) comes from the plate surface or space, and also reflects whether mass (like pollutant diffusion) or energy (such as heat flux generating from the surface) transports through the vortex system or not. So, the pattern of the surface saddle not only links with the vorticity source and strength of the vortex system, but also relates to practical applications such as mass transportation and vortical flow control.

A number of studies (Visbal 1991; Lighthill 1963; Tobak and Peake 1979; Zhang 2005; Wu et al. 2005; Surana et al. 2006; Surana et al. 2008; Surana et al. 2007; Perry and Fairlie 1974) have theoretically contributed to the establishment of separation criteria and to the nature of the outermost saddle point (S_S/S_A) on the surface in juncture flows. Lighthill (1963) described the S₁S₂ as a separation line and proposed a theoretical formulation for separation, beginning with the concept of mass conservation. It postulates that the limit streamlines (streamlines very close to the surface) separate from the surface when both the surface vorticity ($\varOmega$) and the distance (n) between two adjacent skin-friction lines decrease simultaneously. Tobak and Peake (Tobak and Peake 1979) interpreted Lighthill’s description of separation from a perspective of surface shear stress ($\tau_{w}$) and the distance (n). This vivid concept has been broadly applied in the estimation of 3-D flow separation. Zhang (2005) proposed a vorticity-based separation/attachment theory and declared that the convergence of skin-fiction-lines is a necessary but not sufficient condition of separation. Wu et al. (2005) also discussed and developed the vorticity-based separation theory. Surana (Surana et al. 2006, 2007, 2008) derived a separation/attachment criterion which can be evaluated using on-wall measurements of skin friction ($\tau_{w}$) and pressure (p) and they claimed that only four robust separation patterns admit uniquely defined separation lines and surfaces. Perry and Fairlie (1974) mathematically derived the relation between S_S/S_A and the measurable quantities such as surface vorticity, surface pressure and their gradients in different directions.

Some computational results present the existence of S_A in various flow conditions. For the first time, Visbal (1991) numerically identified the existence of “attachment saddle topology” in both steady and unsteady laminar juncture flows and illustrated that generally a convergent skin-friction line is not equivalent to flow separation, as perceived previously. The study showed that different spatial topologies could obtain similar footprint on the surface. Subsequent numerical studies on juncture flows (Hung et al. 1992; Chen and Hung 1992; Rizzetta 1994) indicated that the S_A topology exists over a broad range, including laminar and turbulent, subsonic and supersonic flows.

Some experimental investigations in the past have also observed both attachment and separation saddle point topology. Coon and Tobak (1995) experimentally confirmed the unconventional S_A topology by using a laser light sheet and long-time exposure tracing visualization technique, yet the qualitative method they used still lacked the sufficient spatial resolution to identify the details of flow topology. Zhang et al. (2012a, b), Younis et al. (2014a, b) and Hu et al. (2015) studied the flow topology in the symmetry plane of the juncture flows with the help of quantitative particle image velocimetry (PIV) technique, and the results experimentally confirmed the existence of the unconventional topology presented in Visbal’s simulation results. They analyzed the topological possibility in detail and illustrated that similar skin-friction line pattern could imply several different spatial topological patterns which adds more uncertainties in engineering analysis. They also investigated some parameters which affect the transition of these two types of saddle points.

The researches on separation/attachment saddle points could improve the understanding on flow separation and vortical flows, and the insightful perspective on the mechanism of flow separation could guide the practical applications and conduct flow control better. Despite the work conducted in the past, still a number of problems related to separation/attachment saddle point and separation/attachment criteria have remained unsolved. The topological transition between S_S and S_A and the mechanism behind the transition are not well understood. The perspective of Lighthill on flow separation needs further improvement and requires certain extension of his concept to explain the attachment flow topology. In the present article, two parameters which affect the topological transitions of attachment/separation saddle in laminar juncture flows are investigated. The separation/attachment criterion, based on the surface shear stress ($\tau_{w}$) and distance (n) between skin-friction lines, is also proposed and the flow characteristic analysis is conducted to verify the criterion. The parametric experimental study of topology transition in Hu et al. (2015), is combined with the numerical simulations carried out using commercial CFD package FLUENT, to further investigate the abovementioned problems.

2 Computational statements

The junctures for CFD simulations were constructed with series of different sectional shaped obstacles whose maximum width (W) was varied from 40 to 100 mm. Obstacles having four different cross-sectional shapes, namely an equilateral triangle, a circle, an ellipse with an axis ratio of 1/2 and a square, were adopted to build junctures, as shown in Fig. 2a. The plate length (L) was varied from 150 to 750 mm downstream of the leading edge of the flat plate, a similar setup as in the experiments. The freestream velocity (U_∞) was varied from 1 to 3 cm/s to ensure that the Reynolds numbers based on the obstacle’s maximum width (W), plate length (L) and boundary layer thickness (δ) remained within the following limits: Re_W ≈ 400–3400, Re_L ≈ 1400–25,400 and Re_δ ≈ 190–800, respectively. Here, δ is the thickness of a naturally developed laminar boundary layer on a flat plate without any obstacle being mounted in its way. The value of δ/W was varied from 0.112 to 1.

Fig. 2

a Sectional shapes of obstacles along with the scheme for computational domain with b fixed obstacle end and c free obstacle end immerging in the water

Only half of the domain in the experiment was simulated, where the computational domain length of 300 mm [a little bigger than that of 200 mm in the experiment in water channel (Hu et al. 2015)] from the symmetry plane is provided in lateral direction and downstream domain is extended by a magnitude of 5 W from the trailing edge of the obstacle (Wong and Png 2009). An upstream extension of 500 mm symmetry boundary was set in front of the flat plate leading edge. Two types of computational domains and two types of mesh concentration schemes for each domain were tested before carrying out the detailed simulations. As conducted in Younis et al. (2014c), in one type of domain, the obstacle ends at the top symmetry plane, shown in Fig. 2b; in the other type of domain, the obstacle has free end in the fluid and an extension of 100 mm over the obstacle free end was applied, shown in Fig. 2c.

A structured grid is generated. Besides the mesh concentration near the plate surface where the first grid cell spacing is 0.0005 W, one mesh scheme also concentrates cells near the obstacle; the other scheme concentrates cells near the most upstream singular point. The details of the domains and the mesh schemes are listed in Table 1. The grid distribution is the same in grid A and C, B and D except for the parts lie above the obstacle’s free end. Figure 3 shows the grid sketch of grid C. Figure 3a shows the densified grid around the square sectional obstacle, and the quantity of grid cells in Table 1 indicates half of the part of the figure with symmetry boundary condition applied to the symmetric plane through the center of the obstacle (as shown in Fig. 2c). Figure 3b exhibits the grid on the obstacle surface, and Fig. 3c shows grid on the symmetric plane around the obstacle and the grid over the obstacle’s free end (100 mm immerged in the water according to the water channel experiment).

Table 1 Information of computational grid and domain

Fig. 3

Computational grids a around the obstacle, b on the obstacle and c in symmetry plane

The transient flow calculation is carried out with laminar mode using SIMPLE pressure–velocity coupling, second-order upwind discretization scheme and cell-based gradient option. A non-dimensionalized time step of 0.003 W/U_∞ (Younis et al. 2014c) was specified.

Figure 4 provides the comparison between experimental and computational results with different computational settings. The experiment was conducted using a square section obstacle with maximum width of 80 mm at Re_W = 2177 and Re_δ = 369. Figure 4a illustrates the trends of change in the position of the first and second primary vortices (N₁ and N₂) with the mesh refinement. All the computational results present the similar flow patterns to the experiment except for the size of the vortices and the separation regions. The simulation result obtained with grid C3 almost accurately reflects the structure of the experiment. It implies that the computational results are reliable to conduct further analysis.

Fig. 4

Grid independence study of a position changes of N₁ and N₂ with grid refinement along with b the comparison of experimental and CFD results with Grid A3 and Grid C3

From Fig. 4a, it is also observed that the mesh density has more effect on the flow structures in the singularity region mesh concentrated scheme (grid B and D) than in the obstacle region mesh concentrated scheme (grid A and C). The last two flow structures with mesh concentration in obstacle region (Grid A2 and A3, C2 and C3) are almost the same which means the simulation has hardly affected by the mesh density. When the mesh density rises to certain level, the two mesh schemes with the same domain (grid A3 and B3, C3 and D3) obtain similar structures.

Figure 4b presents the streamline patterns of experiment and simulations with grid A3 and C3. It is evident that the computational results are in good agreement with that of experiment, in both aspects of topological patterns and vorticity distributions.

Comparing the results with symmetric boundary condition at the upper end to those with obstacle free end, the vortex structures with top symmetry boundary condition (Grid A3) are compressed down and the vortices are a little smaller and closer to the obstacle. The free end effect (vortex shedding from the free end of the obstacle) still has weak influence on the topological transition in the simulation, since the topology transition is very sensitive to it when the topology is near critical region of topological transition. To totally eliminate this effect, grid A3 with top symmetry boundary condition is adopted to study the two topology transition parameters (sectional shape of the obstacle and the ratio of boundary layer thickness to the maximum width of the obstacle δ/W). Although the structures are compressed in size, the trends of topology transition in both experiments and simulations are the same. The inherent relation between the on-wall parameters (such as shear stress $\tau_{w}$, skin-friction line distribution, etc.) and the separation/attachment pattern remains unchanged by the above setup.

3 Results and discussions

The outermost topological pattern is affected by many factors (e.g., h/W Younis et al. 2014b). In the present study, as conducted in Hu et al. (2015), two parameters (sectional shape of the obstacle and δ/W) that affect the topology transition are investigated. The simulated topological transformation trends are the same as the experimental ones. Figure 5 shows the outermost topological transition from attachment to separation as decreasing the δ/W (increasing W in Fig. 5). The horseshoe vortex system moves away from the obstacle as increasing W, while the relative position x/W of the system becomes smaller. The left upper column illustrates the topological transition from attachment to separation (from N′ to S′) in the symmetry plane; the right upper column shows the streamline patterns in the symmetry plane and the skin-friction line patterns on the plate surface, and the outermost saddle on the surface transfers from saddle of attachment (S_A) to saddle of separation (S_S). In the left upper column, point C is a critical point from attachment N′ to separation S′. In the right upper column, the contour plots of pressure in the symmetry plane and the streamlines which indicate the vortices and the outermost topologies are adopted. It seems like that the topology transits from attachment to separation as the adverse pressure gradient increase judged from the pressure contour, while detailed investigations show that the separation or attachment of the outermost saddle point depends more on the lateral mass transportation than the streamwise pressure gradients and the relation between the saddle pattern with the pressure distribution is indirect. Figure 5a1 and a2 displays the details of the two topology patterns in which the skin-friction lines on the plate and the limiting streamlines colored by height (color change trend from red to blue indicates that height becomes smaller, and vice versa.) are plotted. From the two figures, it is clearly observed that the streamlines attach toward the plate when pass through a S_A (a1) and separate from the plate when pass through a S_S (a2).

Fig. 5

Topological transition from attachment to separation. The streamline patterns transition in the symmetry plane (left upper column), the outermost saddle transition on the surface (right upper column) and the magnified topology patterns with limiting streamlines colored by height (a1 and a2)

Figure 6 shows the computational saddle points of separation and attachment and the topological transition with different parameters. Figure 6a shows the streamlines in the symmetry plane and the limiting streamlines in a plane very close to the plate surface with the outermost saddles of separation (S_S) and attachment (S_A), respectively. The topology transition is observed to be mainly affected by the sectional shape of the obstacle and δ/W. Figure 6b shows the results of obstacle shape on the topology transition from S_A to S_S with the increase in obstacle bluntness at a fixed value of δ/W. At a fixed value of δ/W, both Re_δ and Re_W are constant, only the obstacle shape is varied to investigate the bluntness effect.

Fig. 6

Topological transition of the outermost singularity with different parameters. a patterns of streamlines in the symmetry plane and limiting streamlines on the plate with the outermost singularity of separation saddle (S_S) and attachment saddle (S_A); and topology transition with b sectional shapes of obstacles, c, dδ/W with fixed δ and varying W and δ/W with fixed W and varying δ, respectively, for square obstacle

The parametric investigation of δ/W at the topology transition was conducted in two separated parts. In the first section, the plate length (L) before the obstacle and the free stream velocity (U_∞) were fixed to obtain constant boundary layer thickness (δ) and only the maximum width (W) of the obstacle was varied; in the second comparative study, W and U_∞ remained fixed and only L was varied to obtain different δ (Hu et al. 2015; Tai and Walker 1991). Figure 6c shows the most upstream nature of the saddle point structure at square obstacle/plate junctures at three different values of Re_δ, where Re_δ is only a function of U_∞, whereas L was kept fixed. At each of the three Re_δ, five values of δ/W are presented with varying W and fixed δ. At a fixed Re_δ (fixed δ), as δ/W decreases (W increases), the outermost topology transfers from attachment to separation. Figure 6d includes three series of comparisons at fixed W and three different Re_W, where Re_W is a function of U_∞ only, whereas W is kept fixed. At each of the three values of Re_W, Re_δ is function of L only (L was varied from 150 to 750 mm) and U_∞ remained fixed. Similar conclusions as Fig. 6c could be obtained from Fig. 6d. At a fixed Re_W (fixed W), as δ/W increases (δ increases), the outermost topology transfers from separation to attachment.

300 Work conditions (4 obstacle shapes, 5 obstacle width W, 5 plate length L and 3 velocity U_∞, 4 × 5×5 × 3 = 300) of experiments were conducted and Fig. 6 only shows a little portion (46/300) of the computation results. A large database of results (not shown here) for various cases with different obstacle shapes, width (W), positions (L) and different free stream velocities (U_∞) also support the topology transition trends showed in Fig. 6.

The results in this section are in consistency with the experimental work (Hu et al. 2015) and provide a valid basis for further in-depth investigation of the separation/attachment criterion.

Figure 7 shows the platform configurations of the computational HSV around different obstacles with λ₂ vortex identification method (Jeong and Hussain 1995), in which the primary vortices are labeled as V1, V2 and V3, respectively, and the vortices among them are secondary vortices. Figure 7a shows the HSV system around different shapes of obstacles with same width W, and Fig. 7b shows the HSV system around square sectional obstacle with different δ/W (fixed δ and increasing W). From Fig. 7, it is observed that the radius of the HSV curvature increase corresponding with the topological transition of the outermost surface saddle from S_A to S_S. The radius of the HSV curvature partly indicates the compression or stretching of the HSV. But the study shows that the radius of the HSV curvature is not a necessary and sufficient condition for the outermost topological pattern, the topological pattern can be different even the radius of the HSV curvature is same when flow conditions are different. Tai and Walker (1991) claim that the three-dimensional separation relates to the ratio of boundary layer kinetic thickness to the equivalent width (δ*/W). The quantitative relationship between the radius of the HSV curvature and the topology pattern needs statistical analysis and the intrinsic control parameter also needs further study. The investigation which focuses on the nature of the topology pattern and the criterion on it is necessary and feasible.

Fig. 7

HSV configurations around different obstacles with λ₂ vortex identification method (λ₂ = − 0.2). a HSV around different sectional shapes obstacle with same width and b HSV around square sectional obstacles with different δ/W (fixed δ and different W)

3.1 Analysis of flow topological transition mechanism and the transition rule

The outermost saddle point (S) on the surface and convergent asymptote S₁S₂ of the skin-friction lines (shown in Fig. 1a) issuing from the saddle are conventionally called separation saddle point (S_S) and separation line, respectively. Tobak and Peake (1979) referred to Lighthill’s (1963) argument (volume flow) to explain why the limiting streamlines in the vicinity of the convergent line leave the surface (separation).

According to Fig. 8a (Tobak and Peake 1979), the separation line S₁S₂ issuing from the saddle point and a rectangular streamtube which consists of two adjacent limiting streamlines (A₁′A₂′ and B₁′B₂′) and their corresponding skin-friction lines (A₁A₂ and B₁B₂) are selected. The streamtube is assumed to be small enough so that the local resultant velocity vectors are almost parallel to the plate and form a linear profile. If n means the distance between the two adjacent limiting lines and h (whose direction is parallel to the η axis of curvilinear coordinates on the surface) is the height of the streamtube, then the mass flux through the streamtube is $\dot{m} = \rho \bar{u}hn = {\text{const}}$, where ρ is the fluid density and $\bar{u}\left( { = \frac{1}{2}u_{\eta = h} = \frac{1}{2}\left( {\frac{\partial u}{\partial \eta }} \right)_{\eta = 0} \cdot h} \right)$ is the mean velocity of the cross section. While the resultant skin friction at the wall is $\tau_{w} = \mu \left( {\frac{\partial u}{\partial \eta }} \right)_{\eta = 0}$, where μ is dynamic viscosity coefficient and is constant in this investigation, hence the mass flux can be written as $\dot{m} = \frac{{h^{2} n\tau_{w} }}{2\nu } = {\text{const}} = C_{1}$, where $\nu = {\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0pt} \rho }$ is kinematic viscosity coefficient, yielding

$$ h = \left( {\frac{C}{{n\tau_{w} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} $$

(1)

where $C = 2\nu C_{1}$.

Fig. 8

Sketch of fluid separation/attachment near the outermost saddle point (S_S/S_A); a flow separation from Tobak (Tobak and Peake 1979); b skin-friction lines near saddle (S) on plate surface; and flow attachment of c upstream of S and d downstream of S

According to Eq. (1), the height of the limiting streamlines above the surface increase rapidly as the flow approaches the separation line for the following two reasons: firstly, the resultant skin friction (τ_w) falls to zero as the saddle point is approached (upstream of saddle); secondly, as the limiting streamlines converge toward the separation line, the distance (n) between two adjacent skin-friction lines decreases rapidly (downstream of saddle).

Abovementioned conception is Tobak and Peake’s explanation about fluid separation near S_S. This idea of 3-D boundary layer separation and Fig. 8(a) have been widely applied and emphasized in the analysis of 3-D boundary layer separation; it is simple and easy to perceive, whereas this concept is not rigorous in expression, for instance, the first reason for separation saddle in the last paragraph. As it is known that Eq. (1) is based on the assumption that the resultant velocity is almost parallel to the surface, this condition becomes void near the singularity (Lighthill 1963), so the validity of the first reason based on Eq. (1) is unconvincing. Besides, since the skin friction at any singularity is zero, the two reasons are also qualified even near an attachment saddle, while the height of the streamtube decreases in an attachment situation. Lighthill’s statement that separation requires the decrease in both $\tau_{w}$ and n, is not appropriate either for saddle of separation or attachment.

Although evaluation criteria of separation/attachment through the direction of normal velocity component (Lighthill 1963) or topological singularity in vertical plane (Perry and Fairlie 1974) have been proposed, the explanation of separation (volume flow) based on Eq. (1) provides a vivid and easily accessible perspective. It is vital to clarify the separation conception mentioned by Tobak and Peake and extend it to explain the existence of attachment saddle.

Equation (1) indicates that the height of the streamtube, h, is not determined by either single n or single τ_w, but the product of n and τ_w. If the product increases, then h decreases and the saddle is attachment S_A; and if the product decreases, then h increases and the saddle is separated S_S.

Figure 8b shows the top view of the saddle (separation/attachment) on the plate surface. Because of the invalidity of Eq. (1) near the saddle (Lighthill 1963), the neighborhood of the saddle point (A_S) is beyond the discussion. The passageway between any two adjacent lines outside of A_S is the base plane of a streamtube corresponding to plane between lines A₁A₂ and B₁B₂ in Fig. 8a. In Fig. 8b, the base of the innermost streamtube, containing the saddle point, could be a plane whose two adjacent skin-friction lines on both sides of the symmetric skin-friction lines pass the saddle (along line s). In the upstream of the saddle point, the distance n approaches to infinity, as the τ_w approaches zero; on the other hand, as n downstream of the saddle point falls down, the skin friction τ_w increases, as is shown in Fig. 8b. Hence the product of n and τ_w in the innermost streamtube might be incremental, constant or decrement, outside of the neighborhood A_S of the saddle point. Likewise, the product in any other streamtube without singularity can also exist in the abovementioned three situations (e.g., in the streamtube along the line s′ in Fig. 8b). Therefore, Tobak’s statement is oversimplified, especially to explain the separation and some supplementary details are required to optimize the vivid perspective of volume flow.

In terms of one-dimensional curvilinear coordinate system (like s) which is collinear with the resultant skin-friction line in any streamtube near the saddle point and directs downstream, n and τ_w can be treated as positive scalar. The skin friction τ_w at the saddle is zero. The type of the saddle point in steady 3-D separation flows is determined by

$$ C_{\text{S/A}} = \frac{{{\text{d}}\left( {n\tau_{w} } \right)}}{{{\text{d}}s}} = \tau_{w} \frac{{{\text{d}}n}}{{{\text{d}}s}} + n\frac{{{\text{d}}\tau_{w} }}{{{\text{d}}s}} $$

(2)

In Fig. 8b, for a saddle point on the plate surface, as the saddle point is approached, $\frac{{{\text{d}}n}}{{{\text{d}}s}} > 0$, $\frac{{{\text{d}}\tau_{w} }}{{{\text{d}}s}} < 0$; as the trajectories leave away from the saddle point, $\frac{{{\text{d}}n}}{{{\text{d}}s}} < 0$, $\frac{{{\text{d}}\tau_{w} }}{{{\text{d}}s}} > 0$. So, the opposite signs of the gradients of n and τ_w determine that the saddle point allows three possible types. Case 1, if $C_{\text{S/A}} > 0$, then the product of n and τ_w increases and h decrease, it is an attachment saddle point S_A. The fluid runs down toward the surface and diverts outward. Similarly, case 2, if $C_{\text{S/A}} < 0$, a separation saddle point S_S arises. The fluid rises up from the surface and rolls into the space. Case 3, if $C_{\text{S/A}} = 0$, it is critical, the fluid diverts outward parallel to the surface.

For the convenience of the following analysis, the symmetric half of the outermost saddle on the plate is divided into the third and fourth quadrants by the convergence asymptote and is further divided into four zones (zones 1 to 4 as shown in Fig. 8b). According to the divergence or convergence of n, the region where the fluid flows from upstream to the convergent asymptote (the third quadrant before and after the saddle) is separated into two zones (zone 1 and 2) and the other region where the fluid flows from the obstacle to the asymptote (the fourth quadrant before and after the saddle) is separated into the other two zones (zone 3 and 4).

The attachment saddle point occurs ($C_{\text{S/A}} > 0$) under two circumstances: firstly, if the effect of the decreasing rate of the resultant skin-friction stress τ_w is eclipsed by the growth rate of n when the saddle point is approached, as shown in Fig. 8c upstream of the saddle (zone 1 or 3); secondly, if positive pressure gradient along the direction outward the symmetry plane allows the acceleration of the lateral mass transportation under which the increment in skin-friction stress τ_w is great enough to counteract and surpass the effect of the decrement in n, when the fluid is transported away from the symmetry plane as the limiting streamlines converge toward the asymptote line, see Fig. 8d, downstream of the saddle (zone 2 or 4).

Likewise, the saddle of separation occurs ($C_{\text{S/A}} < 0$) in two situations: firstly, the divergence of the skin-friction lines (n increasing) upstream of the saddle (zone 1 or 3) is not high enough to cover the effect of that skin-friction stress τ_w decreases; secondly, the convergence of the skin-friction lines (n decreasing) downstream of the saddle (zone 2 or 4) is strong enough to counteract the effect of fluid acceleration (τ_w increasing).

Above analysis on the basis of Eq. (2) is slightly different from other references (Hunt et al. 1978; Lighthill 1963; Tobak and Peake 1979; Surana et al. 2006; Hung et al. 1992; Tai and Walker 1991), and it needs quantitative verification by high-sensitive measurements because the parameters around the singular point become extremely small. According to the best of authors’ knowledge, the present experimental techniques lack the required level of precision in measurements.

So in brief, the skin-friction lines near the S_A exhibit stronger divergence upstream of it and weaker convergence downstream of it than that of S_S. Further mathematical analysis or statistical analysis is imperative to obtain quantitative comparison.

3.2 The numerical simulation verification of flow topology transition rule

The simulation results are used to analyze the theoretical coefficient containing extremely small values of n and τ_w. The lines orthogonal to the skin-friction lines are created to assist the extraction of n and τ_w. The length of the abovementioned line between two extremely adjacent skin-friction lines is n, and the averaged τ_w on that line is determined as the resultant τ_w in Eq. (2). The extracted n and τ_w from the simulation results are substituted into Eq. (2) to verify the topology transition rule proposed in the last section.

From the analysis in the last section, neglecting the situation $C_{\text{S/A}} = 0$, there are four combined flow patterns in one quadrant. Considering the third quadrant (zones 1 and 2) as an example, shown in Fig. 9, and imaging that the streamtube consist of the skin-friction lines pass the S_S/S_A, the adjacent skin-friction line and their corresponding limit streamlines. The limit streamline could consistently separate from the plate from zone 1 to zone 2 (the $C_{\text{S/A}} < 0$ in both zones 1 and 2, Fig. 9a); the limit streamline also could leave away from the plate in zone 1 and attach to the plate after the saddle in zone 2 (the $C_{\text{S/A}} < 0$ in zone 1 and $C_{\text{S/A}} > 0$ in zone 2, Fig. 9b); or the opposite patterns could emerge (always being attachment, Fig. 9c or transferring from attachment to separation, Fig. 9d). The patterns in two quadrants (quadrants 3 and 4) could be the same or be different, therefore, there are more possible combinations of the patterns in the neighboring of the half part of the singularity.

Fig. 9

Sketch showing separation/attachment of streamline and the sign of the coefficient C_S/A in a single quadrant; a separation to separation; b separation to attachment; c attachment to attachment; d attachment to separation

Table 2 provides the states [separation/attachment (S/A) and sign of the coefficient C_S/A] of the outermost singularity in symmetry plane and the neighboring fluid in the four zones. In every juncture presented in Table 2, the signs of the coefficient and the patterns in four zones, are in agreement with the analysis presented in the previous section. Logically, the flow patterns in zones 1 and 3 should be the same as that of the symmetry plane but there is a disharmony in the flow patterns of both zones (cases 2 to 8). Despite differences in flow characteristics between the two lateral sides, zone 1 and 3, yet only one pattern (S or A) can be defined in the symmetry plane. Hence, the flow characteristics in symmetry plane can be judged at macrolevel by observing the direction of spatial streamlines of the convergent asymptote (dash lines in Fig. 9). The differences between two quadrants indicate that the flow pattern is quite close to the critical state of topology transition ($C_{\text{S/A}} = 0$) and the fluids are not fully separated or attached. Only such flow pattern is considered to be in strong separation or attachment mode if all the four zones have the same S or A configuration, like cases 1 and 9. Therefore, in Table 2, only the surface saddles in cases 1 and 9 are total attachment saddle S_A and total separation saddle S_S, respectively.

Table 2 The flow separation/attachment configurations at the outermost surface saddle

Because the precondition of Eq. (1) is not well suited for the region where the singularity exists (Lighthill 1963) (A_S in Fig. 8b), the subsequent separation/attachment criterion based on the sign of the coefficient (Eq. 2) can only provide criterion to the streamtube outside of the saddle, and the researcher can judge by himself that which type of singularity (S_S/S_A) it is through the streamtube very near but outside the singularity. The criterion can also be employed to the whole plate surface, wherever the condition satisfies that the local resultant velocity vectors are almost parallel to the plate and form a linear profile. It is also verified numerically.

4 Conclusions

The laminar juncture flows, with various combinations of obstacle sectional shapes, U_∞, W and L, are numerically simulated. The outermost saddle point of separation/attachment (S_S/S_A) and the topological transition in juncture flows are mainly investigated. The experimental observations can only provide a hint of separation or attachment while the theoretical models based on the concept of limit streamlines cannot be applied because of the rawness of experimental PIV data near the surface. The CFD results provide such means to have better insight into the three-dimensional concepts of topological transition, which otherwise would not have been possible by the use of experiments only.

The numerically simulated results present similar topological transition trends to those of experiments. The outermost topology in the symmetry plane tends to transform from attachment to separation as the bluntness of the obstacle increases or as the ratio of the boundary layer thickness to the maximum width of the obstacle δ/W decreases. The concept of Lighthill’s volume flow theory is further extended and a new decisive coefficient C_S/A is proposed to estimate the separation or attachment of the fluid near the saddle point. The limit streamlines separate from the plate surface if $C_{\text{S/A}} < 0$, whereas they attach to it if $C_{\text{S/A}} > 0$. The proposed relation between the fluid separation/attachment and the sign of C_S/A is verified numerically. A single quadrant in the neighborhood of a saddle is considered for analysis and is further distributed in various zones to study the four dominant separation/attachment modes (constant separation, constant attachment, transferring from separation to attachment and vice versa). The flow will only be considered in fully separated or attached mode if the flow pattern in all four zones is in its corresponding separation or attachment state. The coefficient criterion is applicable to the whole object surface excluding singularities.