1 Introduction

With the development of ultrashort chirped pulse amplification (CPA) [1], one has been able to compress the width of laser pulses to the order of fs and increase the peak power to the order of TW—PW [2]. Pasto et al. [3] define the onset threshold of relativistic motion as 1018 W/cm2, which indicates that the laser field can already reach the relativistic light intensity after the electrons have passed the proper focus, and the electrons, under the action of the relativistic light intensity. The oscillation speed of the laser field is close to the speed of light, and the effect of the magnetic field in the light field on the electron is already comparable to the electric field. Therefore, electrons in such a light field make a nonlinear oscillation motion, and the Thomson scattering becomes a relativistic, nonlinear, and complex problem. The electron can radiate ultra-short x-ray pulses under the action of ultra-short ultra-intense laser pulses and obtain coherent radiation with ultra-short wavelength and ultra-short pulse width, which is of great importance [4, 5] for time-resolved research in medicine, biology, condensed matter physics, and material science.

Because of this, there is a strong interest in nonlinear Thomson scattering [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] in the relativistic case. As early as 1970, Sarachik and Schappert [6] analyzed the harmonic spectrum of nonlinear relativistic Thomson scattering from an initially stationary single electron in two kinds of coordinate systems. Esarey [7] presented the theory of nonlinear Thomson scattering by electron beams and plasmas to intense lasers, and Wang et al. studied the Laguerre-Gaussian circularly polarized Thomson scattering electron trajectory spatial radiation, especially the vortex and symmetric radiation properties [8, 9].

However, the above studies do not address the effect of the carrier envelope phase (CEP) on the temporal and spatial properties of radiation and scattering due to the interaction of relativistic nonlinear TFP laser with electrons at different laser pulse durations. The simulation results show that the CEP has a certain degree of influence on the electron motion, electron normalized energy, and radiation spatial energy distribution, and the influence effect is closely related to the laser pulse duration. In addition, the CEP also affects the radiation optical spectral angular distribution and the pulse time spectral angular distribution of radiation to a certain extent. It is worth noting that the pulse-time spectrum of radiation under the short-pulse laser and the optical spectrum under the long-pulse laser is more obviously affected by the CEP of the laser pulse (Fig. 1).

Fig. 1
figure 1

Geometric diagram of electron interaction with Gaussian laser in rectangular coordinates

Full size image

2 Model building and formula derivation

The normalized vector potential of a focused Gaussian pulsed laser electric field is usually written in the following form [24, 25]:

$$a(\eta )={a}_{0}\mathrm{exp}(-{\eta }^{2}/{L}^{2}-{\rho }^{2}/{b}^{2})({b}_{0}/b)[\mathrm{cos}(\Phi ){\varvec{x}}+\delta \mathrm{sin}(\Phi ){\varvec{y}}]$$
(1)

where \({a}_{0}\) is the normalized amplitude of the laser vector potential, \({a}_{0}=\sqrt{I{\lambda }_{0}^{2}/1.37*{10}^{18}}\), normalized by \(m{c}^{2}/e\), the \(m\) and \(e\) are the rest mass and power of the electron, respectively. \(\delta \) is the polarization parameter, where \(\delta =0\), corresponds to the linearly polarized light, the \(\eta =z-t\), and \({\rho }^{2}={x}^{2}+{y}^{2}\),\( L\) and \(b\) are the pulse widths of the laser, respectively and the radius of the girdle, the \(b={b}_{0}(1+{z}^{2}/{z}_{f}^{2}{)}^{1/2}\), where \({b}_{0}\) is the minimum radius of the pulse and \(b\) is the radius of the bundle waist at which the pulse propagates to \(z\). \({z}_{f}={b}_{0}^{2}/2\). corresponds to the Rayleigh length of this beam, and \(\Phi =\eta +{\Phi }_{R}-{\Phi }_{G}+{P}_{0}, {\Phi }_{R}=\left({x}^{2}+{y}^{2}\right)/\left[2z\left(1+{z}_{f}^{2}/{z}^{2}\right)\right]{, \Phi }_{R}\) is the potential phase associated with the curvature of the wavefront. \(R\left(z\right)=z\left(1+{z}_{f}^{2}/{z}^{2}\right)\) is the radius of curvature of the pulsed laser wavefront, and \({\Phi }_{G}={\mathrm{tan}}^{-1}(z/{z}_{f})\) is the radius of curvature associated with the Gaussian beam from \(-\infty \) to \(+\infty \) when it will undergo \(\pi \) is the Guoy phase associated with the change in phase, and \({P}_{0}\) is the CEP of the laser pulse, which can be set to any value, and the CEP represents the phase of the laser pulse when it meets the electron.

In the above definition, the spatial and temporal coordinates are normalized by \({k}_{0}^{-1}\) and \({\omega }_{0}^{-1}\), \({\omega }_{0}\) and \({k}_{0}\) are the frequency and wave number of the laser, respectively.

In a right-angle coordinate system, the vector potential of the light field can be written as [21]:

$${a}_{x}={a}_{L}\mathrm{cos}(\Phi ),{a}_{y}={a}_{L}\mathrm{sin}(\Phi ),{a}_{z}={a}_{L}\frac{\left.-2x\mathrm{sin}(\Phi +\Theta \right)}{{b}_{0}b}+\frac{\delta 2y\mathrm{cos}(\Phi +\Theta )}{{b}_{0}b}]$$
(2)

where \({a}_{L}=\mathrm{exp}(-{\eta }^{2}/{L}^{2}-{\rho }^{2}/{b}^{2})\left({b}_{0}/b\right), \Theta =\pi -{\mathrm{tan}}^{-1}(z/{z}_{f})\), in fact, when the beam waist radius of the light pulse is larger than \(5{\lambda }_{0}\) when \({a}_{z}\) than \({a}_{x}\), the \({a}_{y}\) is one order of magnitude smaller.

The motion of an electron in an electromagnetic field can be described by the Lagrange equation and the energy equation for the electron [23]:

$${d}_{t}\left({\varvec{p}}-{\varvec{a}}\right)=-{\nabla }_{a}\left({\varvec{u}}\cdot {\varvec{a}}\right), { d}_{t}\gamma ={\varvec{u}}\cdot {\partial }_{t}{\varvec{a}}$$
(3)

where \({\varvec{u}}\) is the velocity of electron, normalized by \(c\), the speed of light. And \({\varvec{a}}\) is the vector potential normalized by \(m{c}^{2}/e\), and \({\varvec{p}}=\gamma {\varvec{u}}\) is the electron momentum normalized by \(mc\), the \(\gamma =(1-{{\varvec{u}}}^{2}{)}^{-1/2}\) is the relativistic factor, and is also the electron energy normalized by \(m{c}^{2}\). In Eq. (3), the \({\nabla }_{a}\) acts only on \(a\). Bringing Eq. (2) into Eq. (3), we can obtain the set of partial differential equations.

$$ \left\{ \begin{gathered} \gamma d_{t} u_{x} = \left( {1 - u_{x}^{2} } \right)\partial_{t} a_{x} + u_{y} \left( {\partial_{y} a_{x} - \partial_{x} a_{y} } \right) + u_{z} \left( {\partial_{z} a_{x} - \partial_{x} a_{z} } \right) - u_{x} u_{y} \partial_{t} a_{y} - u_{x} u_{z} \partial_{t} a_{z} \hfill \\ \gamma d_{t} u_{y} = \left( {1 - u_{y}^{2} } \right)\partial_{t} a_{y} + u_{x} \left( {\partial_{y} a_{x} - \partial_{x} a_{y} } \right) + u_{z} \left( {\partial_{z} a_{y} - \partial_{y} a_{z} } \right) - u_{x} u_{y} \partial_{t} a_{x} - u_{y} u_{z} \partial_{t} a_{z} \hfill \\ \gamma d_{t} u_{z} = \left( {1 - u_{z}^{2} } \right)\partial_{t} a_{z} + u_{x} \left( {\partial_{z} a_{x} - \partial_{x} a_{z} } \right) + u_{y} \left( {\partial_{y} a_{z} - \partial_{z} a_{y} } \right) - u_{x} u_{z} \partial_{t} a_{x} - u_{y} u_{z} \partial_{t} a_{y} \hfill \\ d_{t} \gamma = u_{x} \partial_{t} a_{x} + u_{y} \partial_{t} a_{y} + u_{z} \partial_{t} a_{z} \hfill \\ \end{gathered} \right. $$
(4)

where \({u}_{x}\),\({ u}_{y}\) and \({u}_{z}\) is the number of electrons in the velocity components in the direction of \(x\), \(y\) and \(z\), by solving the above four partial differential equations through Runge–Kutta methods, the coordinates, velocity, acceleration, and the process of energy change with time of the electron in the laser field can be obtained. From the electrodynamics, it is known that the electron doing relativistic accelerated motion will emit electromagnetic radiation, and the radiation energy in unit stereo angle can be expressed as [22]:

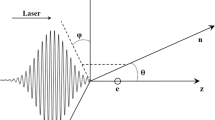
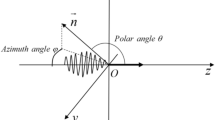
$${E}_{\Omega }=\frac{dW}{d\Omega }={\int }_{0}^{+\infty }\frac{dP(t)}{d\Omega }dt{\prime}={\int }_{0}^{+\infty }\frac{{\left|{\varvec{n}}\times \left[\left({\varvec{n}}-{\varvec{u}}\right)\times {d}_{t}{\varvec{u}}\right]\right|}^{2}}{(1-{\varvec{n}}\cdot {d}_{t}{\varvec{u}}{)}^{6}}dt{\prime}$$
(5)

where \({E}_{\Omega }\) is the energy radiated per unit stereo angle and \({\varvec{n}}=\mathrm{sin}(\theta )\mathrm{cos}(\varphi )\bullet {\varvec{x}}+\mathrm{sin}(\theta )\mathrm{sin}(\varphi )\bullet {\varvec{y}}+\mathrm{cos}(\theta )\bullet {\varvec{z}}\) is the direction of radiation, where \(\theta \) is the polar angle and \(\varphi \) is the azimuthal angle in the spherical coordinates system (\({\varvec{r}}\),\(\theta \),\(\varphi \)). \(t{\prime}\) is the time of interaction between the electron and the laser pulse. The relation between \(t{\prime}\) and \(t\) is given by \(t={t}{\prime}+R, R\sim {R}_{0}-{\varvec{n}}\bullet {\varvec{r}}\), where \({R}_{0}\) is the distance from the origin to the observer and \({\varvec{r}}\) is the position vector of the electron. Electron and laser pulse interaction process, its unit stereo angle per unit frequency interval of radiation energy formula can be expressed by the following formula [22]:

$$\frac{{d}^{2}I}{d\omega d\Omega }=|{\int }_{-\infty }^{\infty }\frac{{\varvec{n}}\times [({\varvec{n}}-{\varvec{u}})\times \dot{{\varvec{u}}}]}{(1-{\varvec{n}}\cdot {\varvec{u}}{)}^{2}}{e}^{is(t-{\varvec{n}}\cdot {\varvec{r}})}\mathrm{d}t{|}^{2}$$
(6)

Of which \(\frac{{d}^{2}I}{d\omega d\Omega }\) was normalized by \({e}^{2}/4{\pi }^{2}c\), \(s={\omega }_{s}/{\omega }_{0}\),\({\omega }_{s}\) is the frequency of the harmonic radiation. By solving Eqs. (5) and (6) it is possible to obtain the full time, full space and full spectral properties of the electron harmonic radiation.

3 Results and discussion

A linearly polarized Gaussian laser is introduced in the nonlinear Thomson scattering frame to collide with a stationary electron, where the laser has a peak amplitude a0 = 2.5 i.e., I = 8.5625*1018 W/cm2, a wavelength λ0 = 1 µm, a pulse width L = 10 fs (for short pulse) or 100 fs (for long pulse), The relation between the pulse width L and the duration τ can be described by τ = L/c, where one wavelength λ0 corresponds to 10/3 fs. For simplicity of analysis, we use L to describe the pulse duration hereafter. Waist radius b0 = 3 µm, for the laser at the z = 0 position, all of which are indicated as being in this case if not otherwise stated in the following.

3.1 Single-electron space dynamics

From Fig. 2(a), (b), it can be seen that under the action of short pulse laser, the electron motion shows apparent regularity, specifically: the electron X–Z motion trajectory shows prominent oscillation fluctuation characteristics, the envelope is elliptical, and with the change in CEP, the electron trajectory along the envelope produces a certain degree of slip. Z-t motion shows the sigmoid function distribution law. The velocity of X and Z direction motion increases and then decreases with time. Finally, the X-direction motion weakens until it disappears, and the electrons move along the Z direction with uniform linear motion. Under the action of the long pulse laser, the electron motion retains the fluctuation characteristics in a specific time range (1000 fs ≤ t ≤ 2000 fs), but the X directional motion time-related convergence disappears and moves along a fixed angular direction, the X component of the directional angle is closely related to the CEP. The angular deflection amplitude shows symmetry about the CEP.

Fig. 2
figure 2

At different CEPs P0, the electron trajectories and electron energy distributions in X and Z directions acted by short pulse laser (a), (c), and long pulse laser (b), (d) are studied

Full size image

From Fig. 2(c), (d), it can be seen that the electron energy distribution shows a more obvious fluctuation under the action of the short-pulse laser, and its outer envelope is nearly semi-elliptical. In addition, for only a limited time (50 fs ≤ t ≤ 150 fs), the electron energy is not 1, which indicates that the short-pulse laser Thomson scattering process mainly occurs in the time range of 50 fs ≤ t ≤ 150 fs. In contrast, under the action of the long-pulse laser, the electron energy no longer shows the same regularity and slip as under the action of the short-pulse laser, and its envelope is no longer regular, but the electron energy distribution law still shows symmetry about the CEP, specifically: the energy distribution of the CEP \({P}_{0}=0\) and \({P}_{0}=\uppi \) overlap ultimately, and the energy distribution of the CEP \({P}_{0} =\uppi /4\) and \({P}_{0}= 3\uppi /4\) shows a very similar trend. However, no matter how the CEP changes, the final energy of electrons converges to about 2.35.

3.2 Angular distribution of the radiation energy

The angular distribution of the energy radiated by the electrons for different laser pulse durations is shown in Fig. 3, projections are added to the 3-dimensional map in order to see the angular distribution properties more clearly. Under the condition of linear polarization, the polarization parameter \(\delta =0\) in Eq. (1), \(a\left(\eta \right)\) is related to the y-directional vector \(\widehat{y}\) is uncorrelated. From Eq. (5), the magnitude of its radiative energy per unit angular radiation energy in the x-direction \({E}_{\Omega X}\) in space is not affected by \(\widehat{y}\) and thus always maintains symmetry, and there is no peak, therefore, in the following, we mainly discuss the radiation properties on the XOZ-plane.

Fig. 3
figure 3

With the short pulse contrast with long pulse of TFP with different CEPs \({P}_{0}\) = 0 (a), (f), π/4 (b), (g), π/2 (c), (h), 3π/4 (d), (i) and π (e), (j) electronic space Angle distribution of radiant energy, the angular energy distribution of the electron is normalized by its maximum value, with the projection at the top

Full size image

It is easy to see that, under the action of long pulse laser, compared to short pulse laser, the energy radiation angle range is broader. In other words, the energy radiated by the short-pulse laser on the electrons is concentrated in a minimal angular range, so its peak energy is also larger. Angular radiation peak shows crescent-shaped, the middle horizontal angle (φ = 0 and φ = 180°) of the peak is the largest, and the peak angle θ is the largest, under the action of short pulse laser, angular radiation peak compared to the angular radiation peak under the action of long pulse is narrower, crescent-shaped bending degree is also lower. Through careful observation, it can be found that radiation energy angular distribution in the long pulse laser action does not meet the fourfold symmetry characteristics, asymmetry phenomenon, and the CEP \({P}_{0}\) related. In contrast, the asymmetry of the angular distribution of radiation energy is not apparent under the action of short-pulse laser.

To explore the radiation asymmetry phenomenon, this paper introduces the concept of radiant energy asymmetry coefficient E0/Eπ, that is, the ratio of the energy accumulated by radiation in φ = 0° to the energy accumulated by φ = 180°. If the asymmetry coefficient is larger, the radiation asymmetry phenomenon is more prominent.

The phenomenon of spatial asymmetry of radiant energy is thoroughly studied from two directions: the angular distribution of forward peak energy and the radiant energy asymmetry coefficient.

In this paper, the forward radiation energy peak exact angle (deviation △θ ≤ 1e-9°) is solved by genetic iterative learning algorithm, and CEP sampling points are obtained as much as possible by GPU accelerated parallelization process. As shown in Fig. 4(a), (b), it is not difficult to find that, although the CEP on the radiation maximum energy angle is not very significant, the angle difference is only in the range of 0.5–1° but has an apparent regularity, the overall trend is similar to the cosine function. The amount of angular change produced by the effect of the CEP under the action of the long-pulse laser is significantly larger than that of the short-pulse laser.

Fig. 4
figure 4

The variation trend of the radiation energy peak angle θ under the action of the short pulse (a) and the long pulse (b) affected by the CEP, the relationship between the radiation asymmetry coefficient and the CEP under different pulse durations (c), and the product of the radiation asymmetry coefficients, whose laser CEP difference is π (d)

Full size image

After that, the distribution of radiant energy asymmetry coefficient under different CEPs was calculated, and from Fig. 4(c), it is easy to see that the radiant energy asymmetry coefficient does not change significantly under the action of the short-pulse laser, while the radiant energy asymmetry coefficient under the action of long-pulse laser shows a particular fluctuation characteristic. The energy asymmetry coefficient first rises to a plateau of slightly greater than one, then increases significantly to reach the maximum value, then falls to a stage of slightly less than one, then decreases significantly to reach the minimum value, and finally upward cycles.

Interestingly, as shown in Fig. 4(d), at two CEP intervals π, the product is very close to the fixed value 1 with a deviation ≤ 2*10–6, thus can be approximated as 1.

According to the correspondence between radiation peak angle and the radiation asymmetry coefficient, we can invert the CEP of the high-energy laser pulse by observing the radiation asymmetry by calculating the radiation asymmetry coefficient combining with the radiation peak angle. This is very helpful for us to determine the CEP of the pulse in the experiment.

3.3 Angular distribution properties of frequency spectra

Next, considering the angular distribution of the radiation optical spectrum at different CEPs, this paper innovatively adopts the full-space spectral angular distribution 3dimensional image as well as polar coordinate projection for the first time to explain the radiation optical spectrum distribution pattern.

From Fig. 5(f)–(j) and (p)–(t), it can be seen that the angular distribution of the radiation optical spectrum under the action of short-pulsed laser is wider, the intensity of the light normalized per unit angle in the angular distribution is higher, and the frequency of the radiation is higher compared with the action of long-pulsed laser. This indicates that the Thomson scattering effect of radiation under the action of short-pulse laser is more significant, which can be explained from the perspective of differences in frequency band ranges with different pulse widths. The bandwidth of short pulse width is wider, and the electron is subjected to laser action with different frequency bands, resulting in a wider spectral range of stimulated radiation of electrons in the laser field.

Fig. 5
figure 5

Comparison of optical spectral angular distribution characteristics. The first row and the third row are the spectral comparison diagrams of short pulse and long pulse in the space rectangular coordinate system, respectively, and the observation angle is 0–180°. The second and fourth rows are the projections of the first and third rows on polar coordinates, the polar angles are from 0 to 90°, and each row shares a colormap. Columns 1 to 5 are when the CEPs \({P}_{0} \)= 0, π/4, π/2, 3π/4 and π, respectively

Full size image

In addition, combined with Fig. 3, it can be found that, under the action of short pulse, the radiation optical spectrum of the primary radiation angle and radiation maximum energy angle is the same, and under the action of short pulse, with Fig. 3 shown that, the radiation energy distribution characteristics are similar. From Fig. 5(a)–(e), it can be seen that the radiation light under the action of the short-pulse laser is less affected by the CEP and only changes in the direction of the non-dominant radiation angle by 10–6 to 10–10. However, the symmetry characteristic of the change about the CEP still exists, specifically, as the CEP \({P}_{0}\) increases, the normalized light intensity in the direction of the non-major radiation angle increases slightly, until \({P}_{0}\) = π/2 reaches the peak, and then decreases according to the original trend.

In contrast, the radiated light under long-pulse laser action is confined to the 0–50ω0 range, and the normalized light intensity is several orders of magnitude lower than that under short-pulse laser action. This indicates that the radiation is more monochromatic in the long-pulse laser action, but it is more difficult to obtain high-energy X-rays through the electron radiation of the long-pulse laser action. As the previous paragraph, the same consistency of the primary radiation angle with the peak radiation direction angle can be found for the long-pulsed laser action in combination with Fig. 3

It is worth noting that the effect characteristics of the radiation optical spectrum under the action of long-pulse laser influenced by the CEP, which are shown in Fig. 5(p)–(t), are similar to those in Fig. 3, the radiation under the action of long-pulse laser is significantly influenced by the CEP, so much so that there appears ‘Dark Angle,’ which is a minimal angle range with the radiation intensity of each frequency is rapidly reduced to a very low value, specifically, in addition to the specific angle, the intensity of surrounding direction of each frequency radiation is significantly stronger than that angle, resulting in the angle almost not radiate light in contrast to others. The ‘Dark Angle’ in the condition of the CEP \({P}_{0}\)= 0 did not appear, but it became the most obvious when \({P}_{0} \)= π/4 and \({P}_{0} \)= π/2. After that, as \({P}_{0}\) increases, the intensity of the forward high-frequency light gradually decreases to the point that the ‘Dark Angle’ is no longer apparent. In addition, the angular size of ‘Dark Angle’ is not consistent for different \({P}_{0}\).

3.4 Angular distribution properties of pulse time spectrum

Next, considering the temporal, spectral angle distribution of radiation pulses at different CEPs, this paper is the first innovative use of full-space, full-time radiation pulse angle distribution 3-dimensional images and logarithmic projection to explain the distribution law of radiation pulses generated by the interaction of single electron and linearly polarized nonlinear intense laser.

From Fig. 6(a)–(e), it is easy to find that the CEP has a very significant effect on the peak of the short-pulsed laser radiation pulses, and the radiation changes from two symmetric pulses when the CEP \({P}_{0} \)= 0 to one prominent single pulse peak and one secondary pulse peak on each side at \({P}_{0}\) = π. The CEP increases from \({P}_{0}\)= 0 until \({P}_{0}\)= π, when radiation pulse angle θ near the radiation maximum energy angle, the pre-pulse peak at t ≈ 90 fs decreases as the CEP increases from \({P}_{0}\), while the post-pulse peak at t ≈ 100 fs then increases, but the latter increase is not significant. Moreover, as shown in Fig. 6(f)–(j), similar to the ‘Dark Angle’ found in the previous section, there is a distinct period of no-pulse time at θ ≈ 90° and t ≤ 65 fs.

Fig. 6
figure 6

Comparison of angular distribution characteristics of radiation pulse time spectrum, the first row and third row are the three-dimensional linear comparison of radiation pulse time spectra under the action of short pulse and long pulse, respectively. The second and fourth rows are the logarithmic projections of the graphs in the first and third rows with a base of 10. The first to fifth columns are when the CEPs \({P}_{0} \)= 0, π/4, π/2, 3π/4, and π, and the observation angle is 0° ≤ θ ≤ 180°

Full size image

It is shown in Fig. 6(k)–(o) that there is no significant effect of the CEP for radiation pulses under the action of long-pulse laser. The radiation pulse time spectrum shows a radial distribution concerning the angle, i.e., the radiation pulse delays its appearance for a short time with increasing angle, which is better reflected in Fig. 6(p)–(t).

It is worth noting that a closer look at Fig. 6(f)–(j) and (p)–(t) reveals that the radiation pulses appear in pairs, and at a specific angle, the pulse pairs pulse pair superpose with interference, connect Fig. 6(a)–(e) with Fig. 6(k)–(o), it is possible to derive the interesting phenomenon that the pulse peaks appear where the pulse pairs overlap entirely.

Comparing Fig. 6(k)–(o) with Fig. 6(a)–(e), it is easy to see that the peak radiation pulses are reduced by 5–7 times compared to the short pulse laser action. It can be concluded that the radiation pulses produced by the short pulse laser have greater intensity but fewer pulses and a shorter overall pulse duration. In comparison, the radiation pulses produced by the long pulse laser have more pulses and a longer overall pulse duration, but the intensity is smaller.

4 Conclusions

This paper investigates the kinetic properties and the spatial radiation of a single electron in a linearly polarized TFP laser field with different pulse durations and CEPs. The full-space radiation energy distribution, the full-angle optical spectrum of forward radiation, and the full-angle pulse time spectrum of forward radiation are innovatively studied in three dimensions. This paper establishes a tightly focused Gaussian laser collision model with stationary electrons using the nonlinear Thomson scattering theory.

The results show that the fourfold symmetry of the spatial distribution of electron radiation is broken, and the energy asymmetry coefficient is closely related to the CEP by the pulse duration. The distribution of the maximum energy angle with the CEP shows a cosine-like variation. In the experiment, we can determine the CEP of the high-energy laser pulse by calculating the radiation space energy asymmetry coefficient with the maximum energy angle mentioned above.

In addition, it is found that the radiation optical spectra’s Thomson scattering effect is more significant under the short-pulse laser, which is more likely to excite high-energy X-rays and even γ-rays, while the monochromaticity is better under the long-pulse laser, but the light intensity is relatively low. The ‘Dark Angle’ phenomenon of the optical spectrum angular distribution under long-pulse lasers was also found, and the phenomenon was found to be closely related to the CEP.

Subsequently, we investigated the characteristics of the temporal spectral angle distribution of radiation pulses and found that the interference superposition phenomenon of radiation pulse pair, especially in short-pulse lasers, which is significantly affected by the CEP. Finally, the number and overall time advantages of electron radiation pulses in long-pulsed laser fields and the peak amplitude advantages of electron radiation pulses in short-pulsed laser fields are proposed to provide a theoretical basis for obtaining specific intensity specific numbers and specific time span of radiation pulses.