1 Introduction

Shear-wave velocity (Vs) structure to a depth of several tens of meters is of fundamental interest in many near surface geophysical studies. Several important geotechnical parameters, such as Vs, 30 (time average shear-wave velocity down to 30 m used in several building codes) and N-value (an index value of formation hardness used in foundation engineering) can be obtained from the Vs structure.

Surface wave methods using artificial sources, such as the spectral analysis of surface waves (SASW) [1] and the multichannel analysis of surface waves (MASW) method [2, 3], have been an efficient tool to determine near surface Vs structure for their nondestructive, non-invasive and environment-friendly properties. In SASW method, usually two vertical geophones spaced out with a distance are used to record the near-field seismic surface waves from an impulsive source, and then the Fourier transformed signals are cross-correlated to yield a dispersion curve reflecting the underground structure beneath the test site. The weaknesses inherent to the method are that it cannot identify Rayleigh wave modes, and its results are sensitive to noise. These limitations could be overcome by using the MASW technique. The overall procedure of the MASW method can be divided into three steps: (1) acquisition of a shot gather in time domain through a multichannel recording system; (2) extraction of reliable dispersion curves by analyzing the acquired records in frequency–velocity domain; (3) inversion of the extracted dispersion curves to estimate Vs profiles.

In usual non-invasive applications of the surface wave method, Rayleigh waves induced by a simple source like hammer strike are recorded in the near-field by using a finite-length linear array of geophones(e.g., [4, 5]). Therefore, the near-field measurements would inevitably be accompanied with a significant amount of unnecessary body wave components as well as a high superposition of the Rayleigh wave modes. Many studies on the surface wave method are thus associated with the techniques available to separate these highly superposed multimode dispersion characteristics and to use the separated modes. For the estimation of dispersion characteristics, here we can recommend some innovative techniques with increasing resolutions, like f–k MUSIC method [6, 7], Multi-offset phase analysis method (MOPA) [8], slant stacking algorithm [9], high-resolution linear Radon transform method [10, 11], and the method based on sparse signal representation and reconstruction (hereafter briefly SSRR method) [12, 13], that have been proposed in last two decades.

The progress in inversion step can be found in its two constitutive procedures, the forward calculation and the optimum model search, respectively. For the forward calculation procedure where the theoretical dispersion curves are calculated from the subsurface earth models, many methods have been used (e.g., the transfer matrix method [14], Knopoff method [15], stiffness matrix method [16], thin-layer stiffness matrix method [17, 18]). The inversion of surface wave phase velocity dispersion curves is a typical nonlinear optimization problem that searches minimum of the nonlinear multidimensional objective function in terms of several subsoil parameters (e.g., S-wave velocity (Vs), P-wave velocity (Vp), density, layer-thickness etc.). This can be solved by using global search method like genetic algorithm [19], or local search method like Levenberg–Marquardt (LM) algorithm [20]. Several effective search algorithms have already been offered in MATLAB Optimization Tool Box (e.g., Trust-region-reflective (TRR) algorithm).

To obtain near-surface 2D or 3D Vs structures is one of the important aspects in recent studies related with the seismic surface wave exploration [21,22,23,24,25,26,27,28,29]. Most of the studies are based on the dispersion curve inversion. In some studies, 2D-Vs sections were generated by aligning all 1D-Vs profiles inverted from dispersion curves for several array measurements at sites along the section line [25, 26]. In other approaches, however, for an array measurement, multiple dispersion curves are extracted from its consecutive trace pairs [27,28,29].

The latter case seems more promising. It has a great potential to improve the horizontal resolution. As an example, in Luo et al. [28], the high-resolution linear Radon transform (LRT) was applied to generate the phase velocity dispersion image and an additional processing was made to reconstruct single-mode records from the separated surface wave modes. This additional process enables to reduce the effects of body waves and other unnecessary modes in the subsequent stages, i.e., extraction of dispersion curves from the single-mode trace pairs and inversions. These two subsequent stages were carried out by applying the SASW method and LM method combined with singular value decomposition (SVD) technique [20] respectively. Their synthetic result showed a good estimation of the near-surface earth model with sinusoidal interface. The real-field result also demonstrated a good coincidence between the estimated model and the pre-determined subsurface section with nearly 9.5° dipping interface.

However, Luo et al. [29] investigated the effectiveness of their approach for mapping subsurface section with dipping interface and concluded that if a slope of interface is greater than 15°, it is difficult to extract high accuracy dispersion curves. The limit of slope seems to be related to the amplitude reduction of Rayleigh wave modes and their superposition in such a largely inclined medium: A significant conversion or diffraction of the Rayleigh waves due to the lateral heterogeneity would occur, resulting lowered wave amplitudes than the case of ideal parallel layered medium. Therefore, a breakthrough to overcome the limit is thought to achieve a high-accuracy dispersion image for the weakened and superposed Rayleigh wave modes.

In this paper we present a scheme to improve the horizontal resolution of the dispersion-based method for 2D-Vs section estimation. We believe that using the updated approaches in all steps of the surface wave method will be a key for enhancing its performance. The scheme is just to apply several updated approaches to all data processing steps as follows: for generation of high-resolution dispersion image and reconstruction of single-mode shot gather, the SSRR method [12, 13] is applied; the cross-correlation method combined with phase-shift scanning [24, 27] is used to extract dispersion curve from a pair of traces in a single-mode shot gather; for the forward calculation we use the thin-layer stiffness matrix method [17, 18]; and for the Vs model search in inversion the TRR algorithm is used. In the following sections, we first introduce the procedure to generate 2D-Vs section by applying the aforementioned updated approaches. The effectiveness of this scheme will be shown through the analysis of the synthetic and real-field data.

2 Procedure to estimate 2D-V s section

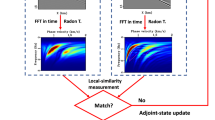
The procedure to estimate the near-surface 2D-Vs section consists of 3 steps: (1) generation of dispersion image and mode separation, (2) extraction of dispersion curves from trace pairs in a single-mode shot gather, (3) inversion of dispersion curves and construction of 2D-Vs section. The approaches implemented in each step are illustrated in Fig. 1.

Fig. 1
figure 1

Schematic representation of the procedure to produce 2D-Vs section and applied approaches in each step

Full size image

2.1 Dispersion image generation and mode separation

As illustrated in Fig. 1, the SSRR method is applied to the generation of phase velocity dispersion image and mode-separation. For a signal \({\mathbf{x}}\), which can be expressed as a vector in a finite dimensional subspace of \({\mathbf{R}}^{N}\), \({\mathbf{x}} = \left( {x_{1} ,x_{2} ,\, \cdots x_{N} } \right)\), the signal can be said k-sparse when only its k elements (k <  < N) are non-zeros [33].

The time-domain seismic signals are first Fourier transformed into frequency domain for later sparse processing. When the surface wave signal induced from a shot source is measured by a linear array of M geophones distributed on the earth surface, the array measurement at frequency \(\omega\) can be written in matrix form as follows (Eq. (10) in [12]):

$${\mathbf{y}} = {\mathbf{Ax}} + {\mathbf{n}}$$
(1)

where \({\mathbf{y}} = \left[ {y_{1} ,y_{2} , \ldots ,y_{M} } \right]^{{\text{T}}}\) is the measured data vector; \({\mathbf{x}} = \left[ {x_{1} ,x_{2} , \ldots ,x_{J} } \right]^{{\text{T}}}\) is the source signal vector consisting of J modal components; \({\mathbf{n}}\) is an \(M \times 1\) noise vector, and \({\mathbf{A}}\) is an \(M \times J\) phase-delay matrix. It contains unknown J modal phase velocities. To solve the Eq. (1), as in [12], it is extended to an overcomplete form under the assumption that the signal is consisted of not the J unknown modes but a redundant number N (N >  > J) of modes with known phase velocities \(\{ c_{1} ,c_{2} , \ldots c_{N} \}\), obtained by sampling a possible velocity range.

Then the \({\mathbf{A}}\) is extended to \(M \times N\) matrix with known elements and \({\mathbf{x}}\) is also assumed to be \(N \times 1\). This overcomplete equation has an infinite number of solutions according to the well-known Kronecker–Capelli theorem. Its physically meaningful solution should be sparse, i.e., it should be expressed as a superposition of only J dominant modes. It can be obtained by using a combined optimization that contain an additional sparsity regularization:

$${\hat{\mathbf{x}}} = \arg \min \left\| {{\mathbf{y}} - {A\tilde{\mathbf{x}}}} \right\|_{2}^{2} + \lambda \left\| {{\tilde{\mathbf{x}}}} \right\|_{1}$$
(2)

In Eq. (2) \({\tilde{\mathbf{x}}}\) denotes all possible estimates, and \({\hat{\mathbf{x}}}\) represents the estimated sparse source signal vector, whose sparsity is controlled by the parameter \(\lambda \,(\lambda \, > 0)\). A 3D-phase velocity dispersion image can be constructed by aligning all the sparse signal amplitude spectra for given frequency range in f–v plane. The mode separation can be done on the dispersion image simply by selecting a mode region and then by muting the other mode ranges.

2.2 Extraction of dispersion curves

For any pair of traces \(y_{1} (f)\), \(y_{2} (f)\) in frequency range, the phase velocity \(V_{R} (f)\) at each frequency f is expressed as follows:

$$V_{R} \left( f \right) = \frac{2\pi f\Delta x}{{\Delta \phi \left( f \right)}}$$
(3)

where \(\Delta x\), \(\Delta \phi \left( f \right)\) are the distance and the phase difference between two traces, respectively. The phase difference \(\Delta \phi \left( f \right)\) can be obtained from the phase information in cross-power spectrum or correlation function between two traces.

Since this SASW based dispersion-curve extraction method is sensitive to noise, the phase-shift scanning is combined with it [24, 27]. After selecting required frequency band \(f \in \left( {f_{\min } ,\,f_{\max } } \right)\) and the phase velocity scanning range \(V_{R} \in \left( {\upsilon_{{{\text{min}}}} ,\,\upsilon_{{{\text{max}}}} } \right)\), the phase differences \(\Delta \phi \left( f \right)\) corresponding to the velocity components in the scanning range at a given frequency can be calculated by the rearranged formula of Eq. (3) \(\Delta \phi \left( f \right) = {{2\pi f\Delta x} \mathord{\left/ {\vphantom {{2\pi f\Delta x} {V_{R} \left( f \right)}}} \right. \kern-0pt} {V_{R} \left( f \right)}}\). By combining the cross-correlation method with phase-shift scanning, the following equation can be obtained [24]:

$$V\left( {V_{R} ,f} \right) = \frac{{P_{21} \left( f \right)}}{{\sqrt {P_{11} \left( f \right)P_{22} \left( f \right)} }}e^{ - i\Delta \varphi \left( f \right)}$$
(4)

In Eq. (4) the first term in the right side is the correlation function between two traces, where \(P_{21} (f)\,\) is the cross-correlation spectrum and \(P_{11} (f)\,,\,P_{22} (f)\,\) are power spectra of each trace. \(V\left( {V_{R} ,f} \right)\) represents the energy corresponding to the phase velocity \(V_{R}\) at a given frequency. The dispersion curve can be extracted by picking the frequency–phase velocity pairs corresponding to the peaks in the dispersion image which is generated by aligning the \(V\left( {V_{R} ,f} \right)\) for each frequency components in f–v domain.

2.3 Inversion and generation of 2D-V s section

We use the thin-layer stiffness matrix method [17, 18] for the forward calculation. The main advantage of this method is that the matrix elements can be written in simple algebraic functions when the soil layers are divided into thin layers with thicknesses less than 1/8–1/10 of the investigated wavelength. And it is also convenient to assemble the global matrix. In particular, the preceding study [17] has shown that the change in density has almost negligible effect in theoretical dispersion curve calculation by the thin-layer stiffness matrix method. This makes it possible to fix the density values properly in inversion.

The phase velocity of Rayleigh waves propagating in the stratified medium can be regarded as a function of four parameters, i.e., Vs, Vp, density, and layer thickness. In inversion, it is important to reduce the number of parameters for computation speed. The most important parameters affecting the Rayleigh wave propagation are S-wave velocity and layer thickness [20]. Here we set only the Vs as an unknown parameter by subdividing the ground model into a reasonable number of thin layers. Vp can be represented by Vs as follows:

$$V_{{\text{P}}} = V_{{\text{S}}} \sqrt {{{2\left( {1 - \nu } \right)} \mathord{\left/ {\vphantom {{2\left( {1 - \nu } \right)} {\left( {1 - 2\nu } \right)}}} \right. \kern-0pt} {\left( {1 - 2\nu } \right)}}}$$
(5)

where \(\nu\) is a Poisson’s ratio: 0.4 when \(V_{{\text{S}}} \le 400\;{\text{m/s}}\), 0.3 for \(400 < V_{{\text{S}}} \le 1500\) and 0.25 for \(V_{{\text{S}}} > 1500\) [30].

The TRR algorithm offered in the optimization toolbox of MATLAB is effective for the problems that have no constraints or only bound constraints. In phase velocity dispersion image, the asymptotes at the high and low frequencies of the fundamental mode approach the phase velocities for the top layer and the semi-infinitive layer, respectively, which can be a sufficient possibility to set the boundary constraints (i.e., upper and lower bounds) of the Vs model. Therefore we establish the inversion problem to estimate the 1D-Vs structure as a nonlinear least-squares problem with optional lower and upper bounds:

$${\mathbf{m}}_{0} = \arg \,\min \left( {\left\| {{\mathbf{E}}\left( {\mathbf{m}} \right)} \right\|^{2} } \right),\,\,\,{\mathbf{m}}_{{\text{L}}} \le {\mathbf{m}}_{0} \le {\mathbf{m}}_{{\text{U}}}$$
(6)

where \({\mathbf{m}}\) is a Vs model, \({\mathbf{m}}_{0}\) is an estimated result, and \({\mathbf{m}}_{{\text{L}}}\), \({\mathbf{m}}_{{\text{U}}}\) are lower and upper bounds of the Vs model respectively. And the \({\mathbf{E}}\left( {\mathbf{m}} \right)\) is expressed as follows:

$${\mathbf{E}}\left( {\mathbf{m}} \right) = \left( {{\mathbf{V}}_{{\mathbf{R}}}^{{{\text{obs}}}} - {\mathbf{V}}_{{\mathbf{R}}}^{{{\text{theo}}}} } \right) \cdot {\mathbf{w}}$$
(7)

where \({\mathbf{V}}_{{\mathbf{R}}}^{{{\text{obs}}}}\) and \({\mathbf{V}}_{{\mathbf{R}}}^{{{\text{theo}}}}\) are observed and theoretically calculated phase velocity values, respectively. And the coefficient vector \({\mathbf{w}}\) is an \(m \times 1\) (m is the number of frequency components) weight vector, where the i-th element is \(w_{i} = \sqrt {{{f_{i} } \mathord{\left/ {\vphantom {{f_{i} } {f_{\max } }}} \right. \kern-0pt} {f_{\max } }}}\) (\(f_{\max }\) means maximum frequency in the considered frequency range). This weight vector is multiplied to avoid the higher misfits that occur at lower frequencies dominate over the smaller ones at higher frequencies. The 2D-Vs section can be mapped by aligning each estimated 1D-Vs profile at the mid-points of corresponding trace pairs. The detailed application procedure is shown through the analysis of the synthetic data.

3 Synthetic examples

To show the effectiveness of the proposed scheme, we use synthetic records simulated by COMSOL Multiphysics 5.4 with an axially symmetric approach for known earth models. All the synthetic shot gathers used in this paper are produced by a 15 Hz (peak frequency) Ricker wavelet applying as a vertical force on the free surface. The gathers are sampled with 1 ms time interval and recording time is 4000 ms. 24-channel shot gathers are simulated, where the nearest offset (distance between source and the first receiver) is 10 m and the receiver spacing is 1 m.

3.1 Model 1: a model with dipping interface

The first model is two-layer elastic earth model with a dipping interface of 20° (Fig. 2a). At the first and the last sensors, the thicknesses from the surface to the interface are about 4.1 m and 12.5 m, respectively. The material parameters in each layer are shown in Table 1.

Fig. 2
figure 2

(a) The image of model with a dipping interface of 20°. (b) 24-channel synthetic shot gather simulated by COMSOL Multiphysics 5.4. The shot gather were muted with 400 m/s (top) and 150 m/s (bottom) to remove the higher-velocity components and the tailing reverberations

Full size image
Table 1 Material parameters of the Model 1
Full size table

Figure 2b shows the simulated 24-channel shot gather in time range from 0 to 800 ms. The spatial attenuation due to geometrical spreading is not corrected. Spectral analysis for the simulated shot gather indicates that the signal lies in 7–40 Hz frequency band and the peak frequencies for each trace varies in the range of 16–22 Hz.

3.1.1 Generation of dispersion image

In this step, high-resolution phase velocity dispersion image is generated from the shot gather by using the SSRR method. After preprocessing to mute the higher-velocity components and the tailing reverberations (data were muted with 400 m/s (top) and 150 m/s (bottom). See Fig. 2b), each trace of the shot gather is transformed into frequency range by Fourier transform. Now the estimation of phase velocity will be carried out at each frequency. First, get \(M \times 1\) measurement vector \({\mathbf{y}}\) in Eq. (1) at given frequency (here M = 24). Then to extend Eq. (1) to an overcomplete form, the signal is assumed to include a redundant number N(N > M) of modes, and the N candidate modal phase velocities are set by sampling the possible velocity range of 100 m/s-500 m/s with 0.5 m/s interval (i.e., N = 801). In terms of the modal velocities we now have the extended \(N \times 1\) complex source signal vector \({\mathbf{x}}\) and extended \(M \times N\) phase-delay matrix \({\mathbf{A}}\):

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} {{{\left( {e^{{{{ - i\omega d_{1} } \mathord{\left/ {\vphantom {{ - i\omega d_{1} } {c_{1} }}} \right. \kern-0pt} {c_{1} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{1} } \mathord{\left/ {\vphantom {{ - i\omega d_{1} } {c_{1} }}} \right. \kern-0pt} {c_{1} }}}} } \right)} {\sqrt {d_{1} } }}} \right. \kern-0pt} {\sqrt {d_{1} } }}} & {{{\left( {e^{{{{ - i\omega d_{1} } \mathord{\left/ {\vphantom {{ - i\omega d_{1} } {c_{2} }}} \right. \kern-0pt} {c_{2} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{1} } \mathord{\left/ {\vphantom {{ - i\omega d_{1} } {c_{2} }}} \right. \kern-0pt} {c_{2} }}}} } \right)} {\sqrt {d_{1} } }}} \right. \kern-0pt} {\sqrt {d_{1} } }}} & \cdots & {{{\left( {e^{{{{ - i\omega d_{1} } \mathord{\left/ {\vphantom {{ - i\omega d_{1} } {c_{N} }}} \right. \kern-0pt} {c_{N} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{1} } \mathord{\left/ {\vphantom {{ - i\omega d_{1} } {c_{N} }}} \right. \kern-0pt} {c_{N} }}}} } \right)} {\sqrt {d_{1} } }}} \right. \kern-0pt} {\sqrt {d_{1} } }}} \\ {{{\left( {e^{{{{ - i\omega d_{2} } \mathord{\left/ {\vphantom {{ - i\omega d_{2} } {c_{1} }}} \right. \kern-0pt} {c_{1} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{2} } \mathord{\left/ {\vphantom {{ - i\omega d_{2} } {c_{1} }}} \right. \kern-0pt} {c_{1} }}}} } \right)} {\sqrt {d_{2} } }}} \right. \kern-0pt} {\sqrt {d_{2} } }}} & {{{\left( {e^{{{{ - i\omega d_{2} } \mathord{\left/ {\vphantom {{ - i\omega d_{2} } {c_{2} }}} \right. \kern-0pt} {c_{2} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{2} } \mathord{\left/ {\vphantom {{ - i\omega d_{2} } {c_{2} }}} \right. \kern-0pt} {c_{2} }}}} } \right)} {\sqrt {d_{2} } }}} \right. \kern-0pt} {\sqrt {d_{2} } }}} & \cdots & {{{\left( {e^{{{{ - i\omega d_{2} } \mathord{\left/ {\vphantom {{ - i\omega d_{2} } {c_{N} }}} \right. \kern-0pt} {c_{N} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{2} } \mathord{\left/ {\vphantom {{ - i\omega d_{2} } {c_{N} }}} \right. \kern-0pt} {c_{N} }}}} } \right)} {\sqrt {d_{2} } }}} \right. \kern-0pt} {\sqrt {d_{2} } }}} \\ \vdots & \vdots & \vdots & \vdots \\ {{{\left( {e^{{{{ - i\omega d_{M} } \mathord{\left/ {\vphantom {{ - i\omega d_{M} } {c_{1} }}} \right. \kern-0pt} {c_{1} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{M} } \mathord{\left/ {\vphantom {{ - i\omega d_{M} } {c_{1} }}} \right. \kern-0pt} {c_{1} }}}} } \right)} {\sqrt {d_{M} } }}} \right. \kern-0pt} {\sqrt {d_{M} } }}} & {{{\left( {e^{{{{ - i\omega d_{M} } \mathord{\left/ {\vphantom {{ - i\omega d_{M} } {c_{2} }}} \right. \kern-0pt} {c_{2} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{M} } \mathord{\left/ {\vphantom {{ - i\omega d_{M} } {c_{2} }}} \right. \kern-0pt} {c_{2} }}}} } \right)} {\sqrt {d_{M} } }}} \right. \kern-0pt} {\sqrt {d_{M} } }}} & \cdots & {{{\left( {e^{{{{ - i\omega d_{M} } \mathord{\left/ {\vphantom {{ - i\omega d_{M} } {c_{N} }}} \right. \kern-0pt} {c_{N} }}}} } \right)} \mathord{\left/ {\vphantom {{\left( {e^{{{{ - i\omega d_{M} } \mathord{\left/ {\vphantom {{ - i\omega d_{M} } {c_{N} }}} \right. \kern-0pt} {c_{N} }}}} } \right)} {\sqrt {d_{M} } }}} \right. \kern-0pt} {\sqrt {d_{M} } }}} \\ \end{array} } \right]$$
(8)

In Eq. (8), the terms \({1 \mathord{\left/ {\vphantom {1 {\sqrt {d_{i} } \,(i = 1,2, \ldots M)}}} \right. \kern-0pt} {\sqrt {d_{i} } \,(i = 1,2, \ldots M)}}\) represent the amplitude decays of surface wave due to geometrical spreading. Real shot gather generally contains only J (J = 2 ~ 3) significant Rayleigh wave modes; thus, the physically meaningful solution \({\hat{\mathbf{x}}}\) should be assumed to be fully sparse. The sparse signal vector \({\hat{\mathbf{x}}}\) was estimated by solving the Eq. (2), where the sparsity regularization parameter λ was adopted 0.45 by trial and error. For solving the convex optimization problem, the program package CVX was used (CVX: MATLAB Software for Disciplined Convex Programming by M. Grant and S.P. Boyd, cvx-w32 version 2.0.1, available at http://cvxr.com/cvx).

Resultant sparse amplitude spectrum of the source signal at a given frequency can be obtained by plotting the \(\log \left| {{\hat{\mathbf{x}}}} \right|\) versus corresponding N mode phase velocities. Figure 3a shows the spectrum at 15 Hz, which indicates that amplitudes corresponding only two phase velocity values among the N-candidate mode phase velocities become dominate. A 3D-graph can be constructed by aligning the spectra for all frequencies. Phase velocity dispersion image can be obtained by projecting the 3D-graph onto the f-v plane (Fig. 3b).

Fig. 3
figure 3

(a) Sparse amplitude spectrum of the source signal at 15 Hz when the sparsity regularization parameter λ in Eq. (2) is selected as 0.45 by trial and error. (b) Phase velocity dispersion image generated by SSRR method. This dispersion image is obtained by aligning the sparse signal spectra for all frequencies. The region surrounded by black dash-dotted line indicates the fundamental mode range. (c) Dispersion image generated by phase-shift method

Full size image

3.1.2 Mode separation and reconstruction of single-mode records

The dispersion image in Fig. 3b shows some dominant “modes,” which reflect a complicated dispersion characteristics of Rayleigh wave propagation in the subsurface medium with dipping interface. To separate reliably the fundamental and higher mode regions on the dispersion image is an important issue for estimation of the 2D-Vs section.

In order to select the mode regions correctly, we suggest to use the dispersion image (Fig. 3c) of phase-shift method [31, 32] from the same shot gather as a reference. From the principle of phase-shift method, the dispersion image can be considered to reflect obviously the velocity distribution range of Rayleigh waves at each frequency. It provides us a good contour when we select any mode region on a highly resolved dispersion image like Fig. 3b. On the reference dispersion image (Fig. 3c), its fundamental mode region has characteristic fairly widened velocity ranges at lower frequencies. Just in the same region on Fig. 3b (contoured with black dash-dotted line), two “modes” estimated by SSRR method are coexisted.

What do these two apparent “modes” coexisting in the fundamental mode region reflect? It is thought that these two “modes” are not generated by the same mechanism as Rayleigh wave modes in parallel stratum because no corresponding parallel layer substructure exists in the ground model (Fig. 2a). It can be explained in relation to Rayleigh wave propagation in the subsurface earth model with dipping interface: A deeply penetrated Rayleigh wave mode propagating through such medium will have different velocities in different parts along the horizontal direction because of the variation of the medium structure. Therefore, we can explain qualitatively that these apparent “modes,” separated on the fundamental mode region, seem to reflect the different phase velocities of a Rayleigh wave mode at different lateral parts of the subsurface section with dipping interface. Thus, the widespread velocity ranges of fundamental mode at lower frequencies below 30 Hz on the dispersion image in Fig. 3c can be regarded as one characteristic that reflect the varying Rayleigh wave propagation in earth structure with sloping interface.

In this way, the fundamental mode range is selected as an area surrounded by black dash-dotted line and y-axis on f–v plane of Fig. 3b, and other higher modes are muted (Fig. 4). Then, the single-mode shot gather shown in Fig. 5a, corresponding to the separated fundamental mode, is reconstructed by Eq. (1).

Fig. 4
figure 4

Separated fundamental mode dispersion image from Fig. 3b

Full size image
Fig. 5
figure 5

(a) Normalized single-mode shot gather reconstructed from the fundamental mode dispersion image. (b) Phase velocity dispersion curves obtained from 22 trace pairs (blue lines) and the theoretical one (red dots) calculated by thin-layer stiffness matrix method for parallel 2-layer earth model where the thickness of the first layer is 8.3 m

Full size image

3.1.3 Extraction of dispersion curves and inversion

Among the 24 single-mode traces with 1 m trace interval (Fig. 5a), we select 22 pairs (trace interval is 2 m) to calculate phase velocity dispersion curves by using the cross-correlation method combined with phase-shift scanning. Figure 5b shows the 22 dispersion curves (blue solid lines) obtained from the trace pairs. Red dots indicate an theoretical dispersion curve calculated for a parallel 2-layer earth model (the thickness of surface layer is 8.3 m, the depth to interface beneath the middle of array in Fig. 2a) by thin-layer stiffness matrix method. The model has the same material parameters as those in Table 1.

Figure 5b makes us confirmed the validity of our aforementioned explanation for the two apparent modes in fundamental mode region of the dispersion image. The dispersion curves distributed in wide velocity range at low frequencies are related to different layer structures along the array line. The upper dispersion curves with relatively high phase velocities at the lower frequency range (< 25 Hz) reflect the propagation of fundamental mode Rayleigh waves which penetrated into the second layer under the sites with shallow surface soil layer (left side in Fig. 2a), whereas the lower ones with low velocities express propagation of the waves under sites with thick surface layer (right side in Fig. 2a). In frequency domain above 25 Hz (where all dispersion curves are converged) the phase velocity values are below 200 m/s, which express that most wave phases in the frequency range propagate through the first layer of the model shown in Fig. 2a.

Then each of these 22 dispersion curves is used as an observed data (i.e., \({\mathbf{V}}_{{\mathbf{R}}}^{{{\text{obs}}}}\) in Eq. (7)) in 1D-Vs profile inversion procedure. In this stage the ground model up to depth of interest (15 m) is divided, as mentioned in Sect. 2.3, into 14 layers with thicknesses of 1 m, and the last layer is considered as a semi-infinitive layer. This makes it possible to proceed the inversion without prior information about the number of layers.

As you can see in Figs. 3b and 4, the asymptotes at the high and low frequencies of the fundamental mode approach the phase velocities for the top layer and the semi-infinitive layer, respectively, so we set the upper and lower bounds (i.e., \({\mathbf{m}}_{{\text{U}}}\) and \({\mathbf{m}}_{{\text{L}}}\) in Eq. (6)) as 400 m/s and 200 m/s, respectively. And the initial Vs model is set as a vector of 15 evenly spaced values in the interval between the upper and lower bounds.

Finally 22 1D-Vs profiles obtained by solving the Eq. (6) are aligned at the mid-points of each pair to construct a pseudo-2D Vs section (Fig. 6). This pseudo-2D Vs section shows the dipping interface clearly, which is consistent with the dipping interface of 20° (black dash-dotted line) in Fig. 2a.

Fig. 6
figure 6

2D-Vs section generated by inverting the 22 dispersion curves, and the black dash-dotted line representing the dipping interface in Fig. 2a

Full size image

3.2 Model 2: a single step-shaped earth model

The second model is a two-layer earth model with single step-shaped interface (Fig. 7a), which can be used to model a fault with vertical displacement. The depths from the surface to the step line are 4 m at the left side and 8 m at the right side, respectively. The material parameters for each layers are the same with those in Table.1.

Fig. 7
figure 7

(a) Image of a single step-shaped earth model. (b) Inverted pseudo-2D Vs section and the step-shaped interface (black dash-dotted line). (c) Phase velocity dispersion image based on SSRR method and selected fundamental mode range (black dash-dotted line). (d) Dispersion image generated by phase-shift method

Full size image

24-channel shot gather simulated for the earth model was processed in the same way as in Model 1. From the estimated dispersion image (Fig. 7c), fundamental mode shot gather was reconstructed, and 23 dispersion curves were obtained from 23 consecutive trace pairs (trace interval is 1 m). The depth to be investigated was set as 10 m and the dispersion curves were inverted to generate a 2D-Vs section (Fig. 7b). The estimated 2D-Vs section shows a good agreement with the true model (black dash-dotted line).

As in Fig. 3b, characteristic highly resolved two apparent modes are again appeared in fundamental mode range surrounded by black dash-dotted line in Fig. 7c. The fundamental mode range was selected based on the dispersion image by phase-shift method (Fig. 7d) as we suggested above. These two apparent modes in the fundamental mode range also reflect the different phase velocities of a Rayleigh wave mode at different lateral parts in Fig. 7a.

4 A real-field example

In this section we apply the proposed method to a real-field data. The real-field data were acquired at a urban construction area in northern part of our country in July of 2018. The experiment site contains pumice sand layer sandwiched between a modern surface sandy soil layer (upper layer) and an old clay-loamy soil layer developed on the underlying basalt layer.

A 12-channel shot gather (Fig. 8) was acquired using a linear array of 10 Hz vertical component geophones. The geophone interval was 2 m and the nearest-offset was 5 m. Seismic waves induced by 5 kg sledgehammer striking were recorded for 8 s with 200 Hz sampling frequency.

Fig. 8
figure 8

12-channel real-field shot gather. The data were muted with 800 m/s (top) and 50 m/s (bottom) to enhance surface waves before generating a dispersion image by SSRR method

Full size image

The acquired shot gather was processed in the similar way as in synthetic data processing. Figure 9 shows the dispersion image generated by SSRR method, where the region enclosed by black-dashed line is the selected fundamental mode range. From the reconstructed fundamental mode shot gather, 11 dispersion curves for consecutive trace pairs were extracted.

Fig. 9
figure 9

Phase velocity dispersion image generated by SSRR method and selected fundamental mode range (black-dashed line)

Full size image

For inversion, an initial earth model with 13-layers was set, which included the top 12-thin layers with same thickness of 0.5 m and an underlying half space. The upper and lower bounds of the Vs model were selected as 900 m/s and 100 m/s, respectively. The resultant pseudo-2D-Vs section is shown in Fig. 10. This 2D-Vs section (Fig. 10) shows that bed rock lies at about 4 m depth and a low-velocity layer with S-wave velocity of about 100 m/s is sandwiched between two layers with slightly higher velocities than it, which is well consistent with drilling data. The sandwiched layer appears to be slightly thicker on the left part (< 8 m from the first geophone), which may be related to the fundamental mode dispersion curve that is branched into two in frequency range below 20 Hz in Fig. 9.

Fig. 10
figure 10

2D-Vs section generated from 12-channel real-field data

Full size image

5 Conclusions

In this paper, we showed an attempt to improve the performance of subsurface 2D-Vs imaging based on the dispersion analysis of seismic surface waves. Several updated approaches were applied to overall data processing stages, i.e., the generation of phase velocity dispersion image, reasonable mode separation, calculation of forward problem and the last procedure for inversion of dispersion curves. Synthetic examples and real-field data demonstrated the effectiveness and applicability of the proposed attempt. In the synthetic case, dispersion image by SSRR method revealed characteristic two highly resolved apparent “modes” on the fundamental mode region. We described the phenomenon as follows: The “modes” reflect the different phase velocities of a Rayleigh wave mode at different lateral parts of the laterally heterogeneous media. We think that each of the applied approaches played its own role for improvement of the method. For all that, it is desirable to give importance to the application of the SSRR method. It helped us to have a highly resolved image on Rayleigh wave propagation in the laterally heterogeneous medium.