1 Introduction

LiNbO3 and LiTaO3 are two well-known ferroelectrics which possess among the highest spontaneous polarizations of all ferroelectrics. They have been the subject of intense study due to their many applications in the electro-optical, optical and piezoelectric fields. These materials that show a ferroelectric behavior are well known to be narrow-range nonstoichiometric compounds. In LiTaO3, the solid solubility range extends from about 46–50.4 mol% of Li2O at room temperature [1]. The structure of ferroelectric LiTaO3 and that of LiNbO3 belong to space group R3c and can be considered as a superstructure of the α-Al2O3 corundum structure with Li+ and Ta5+ cations along the c-axis [2]. Recently, several workers have investigated the growing of high-quality single crystals of stoichiometric LiTaO3 and LiNbO3 which exhibit considerably wide nonstoichiometry at high temperature. Using the chemical bond method, a comprehensive description of the defect and the chemical bonding structure has been proposed by Xue et al. [3, 4].

To find which defect is involved in this phenomenon, we have proposed a theoretical description of the defect structure in LiTaO3 and LibO3 on the basis of a set of vacancy models combined with a ferroelectric phase transition theory. As LiTaO3 is isomorphous with LiNbO3, several defect models have been proposed for LiNbO3.

Fay et al. [5] describe a ceramic sample assumed containing oxygen and lithium vacancies by the oxygen vacancy model having a formula [Li1−2xV2x][Nb][O3−xVx] where [Li] represents the sublattice and V denotes the vacancies. This model cannot describe the density variation in function of the composition. In order to correct this anomaly, Lerner et al. [6] have predicted that an excess of niobium ions might occupy the lithium sites. This is the lithium vacancy model, which is given by the formula [Li1−5xNbxV4x][Nb]O3 where the lithium vacancies are introduced taking into account the charge compensation. However, Peterson and Carnevale [7] observed a new defect structure corresponding to the Nb-site vacancy type using the NMR technique. Then, their niobium vacancy model is arranged as follows: [Li1−5xNb5x][Nb1−4xV4x]O3. Contrarily to the result pointed out by Abrahams and Marsh [8], Donnerberg et al. [9] proved that the niobium vacancy model is unfavorable to compare the energetic aspect of the defect structure models. A comparative study between the densities of these models allows Iyi et al. [10] to reject the oxygen vacancy model.

A theory of ferroelectric’s phase transition in the crystal LiNbO3 has been performed to understand and predict the properties of this crystal [11]. In this system, the solution of the dynamic problem of the crystal planes system exhibits the existence of the “soft mode” at the ferroelectric’s transition.

For example, this method has been applied to the defect structure analysis of the lithium niobium single crystals [12] and lithium tantalate [13]. These studies provide a useful understanding of the phase transition dynamic behavior and the normal defect structure of LiBO3 (B = Nb, Ta) [14].

Abdi et al. presented a complete model of the structure of intrinsic defects in LiNbO3, based on Raman spectroscopy results. It is based on the coexistence of lithium (VLi) and niobium (VNb) vacancies. The reliability of this model and the associated calculations were verified by analyzing the frequencies and depreciation phonon modes, reinforced by Raman scattering measurements recorded in crystals of various compositions. They show that the Li vacancy is dominant in the structure of defects incongruent crystals [15].

The main aim of the present work is to investigate the defect structure in ilmenite-type lithium niobate and lithium tantalate and give a comparison between normal and ilmenite-type LiBO3 (B = Nb or Ta).

Several experimental and theoretical studies have been developed on this subject and are mentioned in [9, 16, 17]. For example, in the work of Kong et al. [18], a weak peak at about 738 cm−1 reported as a very strong Raman peak of ilmenite phase LiNbO3 was observed for nonstoichiometric LiNbO3 crystals. However, Kumada et al. [17] have prepared the ilmenite-type structural LiNbO3 by the ion exchange reaction in the molten salt NaNbO3. Above a threshold temperature (500 °C), the structure of this new compound changes from the ilmenite to the LiNbO3 type.

These results pushed us to propose a theoretical approach to study the defect structures of ilmenite-type LiBO3 (B = Nb or Ta). This will allow us to give a comparison between the calculated normal and ilmenite values and the experimental data of the Curie temperature for the three vacancy models.

In this work, we present a description of the theoretical approach to study the Curie temperature of normal and ilmenite-type LiBO3 (B = Ta, Nb) [14]. A detailed comparison between calculated values of the normal and ilmenite-type LiBO3 and the experimental data of the Curie temperature is proposed in this paper.

2 Theoretical approach

2.1 The ilmenite structure

In the past, different models have been proposed in order to describe the accommodation of Li2O deficiency in LiNbO3. In what follows, we may omit the discussion of the model related to oxygen vacancies [5]. This contradicts the observed density changes upon increasing the nonstoichiometric. The two remaining models consider all compensating defects to occur on the cationic sublattices:

$$ '{\text{LiNbO}}_{3} ' \to 3{\text{Li}}_{2} {\text{O}} + {\text{Nb}}_{\text{Li}}^{4 \bullet } + 4{\text{V}}_{\text{Li}}^{\text{I}} - {\text{LiNbO}}_{3} $$
(1)
$$ '{\text{LiNbO}}_{3} ' \to 3{\text{Li}}_{2} {\text{O}} + 5{\text{Nb}}_{\text{Li}}^{4 \bullet } + 4{\text{V}}_{\text{Nb}}^{{5{\text{I}}}} - {\text{LiNbO}}_{3} . $$
(2)

Donnerberg [19] has used Kroger–Vink notation [20] to formulate these chemical solid-state reactions. In addition, LiNbO3 denotes the whole bulk of perfectly grown LiNbO3. Model (1) corresponds to the chemical sum formula Li1−4xNb1+xO3, and model (2) to (Li1−5xNb5x) Nb1−4xO3.

The most obvious difference between reactions (1) and (2) relates to the concentration of niobium antisite defects \( ({\text{Nb}}_{\text{Li}}^{{ 4 {{ \bullet }}}} ) \) and to the occurrence of Li or Nb vacancies.

In order to satisfy the experimental results of Abrahams and Marsh [8], Smyth [21] proposed the formation of appropriate defect clusters. Starting with the reaction

$$ '{\text{LiNbO}}_{3} ' \to 3{\text{Li}}_{2} {\text{O}} + {\text{Nb}}_{\text{Li}}^{4 \bullet } + 4({\text{Nb}}_{\text{Li}}^{4 \bullet } {\text{V}}_{\text{Nb}}^{{5{\text{I}}}} ) - {\text{LiNbO}}_{3} , $$
(3)

which immediately follows from Eq. (2) by a few re-arrangements, Smyth observed that the defect complexes \( 4({\text{Nb}}_{\text{Li}}^{4 \bullet } {\text{V}}_{\text{Nb}}^{{5{\text{I}}}} ) \) may be interpreted as basic Li vacancies within ilmenite-structured LiNbO3, because perfect and ilmenite-structured LiNbO3 differs only by their cation stacking sequence along the crystallographic c-axis, i.e.,

  • …BLi□BLi□BLi□BLi□BLi… perfect model

  • …BLi□LiB□BLi□LiB□BLi… Ilmenite model

Respectively, in this representation □ denotes a structural cation vacancy. The Li vacancies would be related to the LiB units. A necessary condition of this model to become favorable is that perfectly grown LiBO3 and the ilmenite structure LiBO3 are energetically almost equivalent.

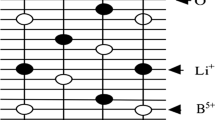
In this work, we suppose that the ceramic samples of ilmenite-structured LiBO3 (B = Ta or Nb) consist of single crystal on the basis of their structure. Such an assumption is based on the experimental fact that the ferroelectric phase transition occurred in the ceramic samples which are formed by parallel planes along the polar “c” axis. The projection of an elementary cell of ilmenite-type LiBO3 on a plane, where the polar axis c lies, is shown in Fig. 1.

Fig. 1
figure 1

Different planes in an elementary cell of crystal ilmenite LiBO3

Full size image

2.2 Soft mode frequency and Curie temperature

The new approach proposed by Safaryan [11] on ferroelectric transition in the crystal LiNbO3 as well as by Masaif [13] on ferroelectric transition in the LiTaO3 is tested from new results in order to discuss the main role of the nonstoichiometric compositions in the ilmenite-structured LiBO3 compounds.

This approach [11, 12] manifests itself as a new tool to describe the defect structure mechanism in the ilmenite of lithium tantalate and lithium niobate where several physical quantities are relatively sensitive to the nonstoichiometric composition. For this purpose, it was necessary to initially find the part of the potential energy of interaction between the electrically charged planes. This interaction is responsible for the restoring force against the relative movement of the planes around their equilibrium positions.

The energy of the electrostatic interaction of two charged long lines is:

$$ W = e^{2} \delta_{i} \delta_{j} b^{2} \ln \frac{2l}{{R_{ij} }} $$
(4)

where \( \delta_{i} = \frac{{N_{i} q_{i} }}{l \, b} \) with l, Rij, qi and Ni are the line length, the distance between the lines, the charge of ions and their number, respectively. We consider also the energy of repulsion between planes that can be put in the form \( {{B_{ij} } \mathord{\left/ {\vphantom {{B_{ij} } {R_{ij}^{n} }}} \right. \kern-0pt} {R_{ij}^{n} }} \) where n is large (6–10 for ionic crystals). We deduce the full energy of interaction of planes such as:

$$ U_{ij} = - \frac{{e^{2} q_{i} q_{j} }}{b}\ln \frac{2l}{{R_{ij} }} + \frac{{B_{ij} }}{{R_{ij}^{n} }} $$
(5)

Differentiating (5) for Rij, we find the interaction force between planes. From the equilibrium condition (\( U_{ij}^{\prime } = 0 \)), we find the coefficient Bij,

$$ B_{ij} = \frac{{e^{2} q_{i} q_{j} }}{b \, n}(R_{ij}^{0} )^{n} $$
(6)

where \( R_{ij}^{0} \) is the equilibrium distance between planes. Substituting (6) in (5), we can then expand the potential energy in terms of plane displacements from equilibrium positions \( x_{ij} = R_{ij} - R_{ij}^{0} \). For Uij, we receive up to the second order

$$ U_{ij} = \frac{{e^{2} q_{i} q_{j} }}{b}\left( {\frac{1}{n} - \ln \frac{2l}{{R_{ij}^{0} }}} \right) + \frac{{e^{2} q_{i} q_{j} n}}{{b \, (R_{ij}^{0} )^{2} }} \, \frac{{x_{ij}^{2} }}{2} $$
(7)

The coefficient \( C_{ij} = \frac{{e^{2} q_{i} q_{j} }}{{b \, (R_{ij}^{0} )^{2} }}n \) describes the interaction between Li and O planes (as well as for Ta and O).

However, the interaction between Li and Ta (Nb) will deduce from the total energy:

$$ U_{ij} = \frac{{e^{2} q_{i} q_{j} }}{b}\ln \frac{2l}{{R_{ij}^{0} }} - \frac{{B_{ij} }}{{R_{ij} }} $$
(8)

Finally, for LiBO3 crystal Cij coefficients are

$$ C_{ij} = \frac{{e_{{}}^{2} q_{i} q_{j} }}{{b \, (R_{ij}^{0} )_{{^{{}} }}^{2} }}n $$
(9)

Having the energy of interaction of planes per ion (5), Safaryan [11] and Masaif [13] reduced the dynamic problem of vibration of the system of charged planes to a problem of vibration of linear lattice, the unit cell of which (with parameter a) has three particles: Li1+, B5+ and 3O2−. Let us denote the displacements of these particles in the sth unit cell through μs, vs and χs correspondingly (Fig. 2-a).

Fig. 2
figure 2

(a) Linear lattice of ions Li+, B5+ and triangle of ions O2− replacing the system of crystal planes. (b) Displacement of Li+, B5+ and 3O2− ions in a linear lattice of the ilmenite type

Full size image

To solve the dynamic problem, we reduced the ilmenite type of the charged planes to a system of vibration of linear lattice (Fig. 2-b).

$$ {\text{with}}\quad a = a^{\prime } + a^{\prime \prime } $$

In the lattice of equilibrate structure: a′

$$ C_{\text{Li - O}} \equiv C_{20} = - 3\frac{{q_{0} q_{2} e^{2} }}{{b \, R_{20}^{2} }}n, $$
(10)
$$ C_{\text{B - O}} \equiv C_{10} = - 3\frac{{q_{0} q_{1} e^{2} }}{{b \, R_{10}^{2} }}n, $$
(11)

and

$$ C_{\text{Li - B}} \equiv C_{21} = \frac{{q_{1} q_{2} e^{2} }}{{b \, R_{21}^{2} }}n. $$
(12)

where q1, q2 and q0 are, respectively, the electric charges of B5+, Li+ and O2− ions.In the lattice of the disordered structure: a″

$$C^{\prime }_{{\text{Li-O}} }\equiv C^{\prime }_{20}=-3\frac{{q_{0}q_{2} e^{2} }}{{b\,R^{\prime }_{20}}}n,$$
(13)
$$ C_{\text{B - O}}^{\prime } \equiv C_{10}^{\prime } = - 3\frac{{q_{0} q_{1} e^{2} }}{{b \, R_{10}^{\prime 2} }}n, $$
(14)

and

$$ C_{\text{Li - B}}^{\prime } \equiv C_{21}^{\prime } = \frac{{q_{1} q_{2} e^{2} }}{{b \, R_{21}^{\prime 2} }}n. $$
(15)

In the study of ilmenite structure, we observe that the unstable part a′ is defined by: BLiO. We must seek to find points of equilibrium between these ions, where \( R_{ij}^{\prime } \) are the distances between separated ions.

The displacements of the three ions are indicated by vs (Li+), us (B5+) and χs (O2−). Then, the system is described by the differential equations as

$$ \begin{aligned} (2M_{2} \omega^{2} - C_{12} - C_{02} - C_{12}^{'} - C_{02}^{'} )u + (C_{12}^{'} + C_{12}^{{}} )v + (C_{02} + C_{02}^{'} )x & = 0 \\ (C_{01} + C_{12}^{'} )u + (2M_{1} \omega^{2} - C_{12} - C_{01} - C_{12}^{'} - C_{01}^{'} )v + (C_{12} + C_{01}^{'} )x & = 0 \\ (C_{02} + C_{02}^{'} )u + (C_{01} + C_{01}^{'} )v + (2M_{0} \omega^{2} - C_{01} - C_{01}^{'} - C_{02} - C_{02}^{'} )x & = 0 \\ \end{aligned} $$
(16)

The determinant of Eq. (16) is written:

$$ \begin{aligned} \Delta & = M_{0} M_{1} M_{2} \omega^{6} - [M_{0} M_{1} (C_{12} + C_{20} ) + M_{1} M_{2} (C_{10} + C_{20} ) + M_{0} M_{2} (C_{12} + C_{10} )]\omega^{4} \\ & \quad + [(C_{10} C_{12} + C_{10} C_{20} + C_{12} C_{20} )(M_{0} + M_{1} + M_{2} )]\omega^{2} \\ \end{aligned} $$
(17)

where M1, M2 and M0 are, respectively, the masses of the elements B, Li and O. The choice of solutions in the form of plane waves

$$ g_{\text{s}} = g\,{\text{e}}^{i(\omega \, t + a \, s \, k)} \quad {\text{with}}\,g = u,v\,{\text{or}}\,\xi $$
(18)

leads to a system, of linear equations, which has a nontrivial solution.

In order to obtain the fundamental frequencies of the optical branches, we put k = 0 in the determinant equation (Δ = 0). Then, we get the following equation:

$$ \omega^{4} + F\omega^{2} + S = 0 $$
(19)

where

$$ \begin{aligned} F & = - \frac{{C^{'}_{01} }}{{2M_{0} }} - \frac{{C^{'}_{02} }}{{2M_{0} }} - \frac{{C_{01} }}{{2M_{0} }} - \frac{{C_{02} }}{{2M_{0} }} - \frac{{C^{'}_{01} }}{{2M_{1} }} - \frac{{C^{'}_{12} }}{{2M_{1} }} - \frac{{C_{01} }}{{2M_{1} }} - \frac{{C_{12} }}{{2M_{1} }} - \frac{{C^{'}_{02} }}{{2M_{2} }} - \frac{{C^{'}_{12} }}{{2M_{2} }} - \frac{{C_{02} }}{{2M_{2} }} - \frac{{C_{12} }}{{2M_{2} }} \\ S & = \left( {\frac{1}{{4M_{0} M_{1} }} + \frac{1}{{4M_{0} M_{2} }} + \frac{1}{{4M_{1} M_{2} }}} \right)I + \frac{1}{{4M_{0} M_{1} }}J + \frac{1}{{4M_{0} M_{2} }}K + \frac{1}{{4M_{1} M_{2} }}L \\ \end{aligned} $$

and

$$ \begin{aligned} I & = (C^{'}_{01} C^{'}_{02} + C^{'}_{01} C^{'}_{12} + C^{'}_{02} C^{'}_{12} + C^{{}}_{02} C_{01} + C^{'}_{01} C_{02} \\ & \quad + C^{'}_{12} C_{02} + C_{01} C_{02} + C^{'}_{02} C_{12} + C_{12} C_{02} + C^{'}_{12} C^{'}_{01} ) \\ J & = (C_{01}^{2} + C^{'}_{01} C_{01} + C_{02} C^{'}_{12} ) \\ K & = (C^{'}_{12} C_{01} + C_{01}^{{}} C_{12} + C^{'}_{01} C_{12} ) \\ L & = (C^{'}_{01} C_{12} + C^{'}_{12} C_{12} + C_{12}^{2} ) \\ \end{aligned} $$

The optical modes are given by

$$ \omega_{{}}^{2} = - \frac{1}{2}F - \frac{1}{2}(F^{2} + 4S)^{1/2} $$
(20)
$$ \omega^{2} = - \frac{1}{2}F + \frac{1}{2}(F^{2} + 4S)^{1/2} $$
(21)

At 0°K, the soft mode frequency ω2 is proportional to the Curie temperature Tc. Substituting ω2 by expression (21), the following relation that allows calculating the Curie temperature is obtained:

$$ T_{\text{c}}^{*} = \frac{{F^{*} - \sqrt {F^{*2} + 4 \times S^{*} } }}{{F - \sqrt {F^{2} + 4 \times S} }}T_{\text{c}} $$
(22)

The element X represents the exactly stoichiometric compositions, and X* is the nonstoichiometric composition. Formula (22) allows us to calculate the Curie temperature for the different models. This will permit a comparison between this data and the experimental values. However, we represent these models, described previously, in the following condensed form.

\( [{\text{Li}}_{{\alpha_{1} }} B_{{\alpha_{2} }} \theta_{{\alpha_{3} }} ][B_{{\beta_{1} }} \theta_{{\beta_{2} }} ][O_{{3\gamma_{1} }} \theta_{{\gamma_{2} }} ] \); and \( K^{*} = g\,K \) with K = M, q and g = α, β or γ. Here, α, β and γ allow identifying the three models as follows:

  1. 1.

    Oxygen vacancy model corresponds to α1 = 1 − 2x, α3 = 2x, β1 = 1, γ1 = 1-x/3 and γ2 = x; and \( K_{2}^{*} = \alpha_{1} K_{2} ,K_{1}^{*} = \beta_{1} K_{1} \) and \( K_{0}^{*} = \gamma_{1} K_{0} \).

  2. 2.

    Tantalate or niobate vacancy model corresponds to α1 = 1 − 5x, α2 = 5x, β1 = 1 − 4x, β2 = 4x and γ1 = 1; and \( K_{2}^{*} = \alpha_{1} K_{2} + \alpha_{2} K_{1} ,K_{1}^{*} = \beta_{1} K_{1} \) and \( K_{0}^{*} = \gamma_{1} K_{0} \).

  3. 3.

    Lithium vacancy model corresponds to α1 = 1–5x, α2 = x, α3 = 4x, β1 = 1 and γ1 = 1; and \( K_{2}^{*} = \alpha_{1} K_{2} + \alpha_{2} K_{1} ,K_{1}^{*} = \beta_{1} K_{1} \) and \( K_{0}^{*} = \gamma_{1} K_{0} \).

In this representation, α = β = γ = 0 means that ions and vacancies are absent in these nonstoichiometric models. The oxygen vacancy model is constructed taking into account the charge compensation for ilmenite structure in the nonstoichiometric LiBO3 by the oxygen and the lithium vacancies. However, the tantalate (or niobate) vacancy model is arranged so that the vacancy does not exist in the Li site but in the Ta (or Nb) site.

In order to provide an adequate description of the defect ilmenite structure in nonstoichiometric LiBO3, we have analytically performed the calculations of different physical quantities which are illustrated in Table 1. Estimates of \( T_{\text{c}}^{*} \) for Li (Ta or Nb) O3 have been obtained by using the following values of the charges and the masses of ions: qO = q0 = 2, qTa = qNb = q1 = 5, qLi = q2 = 1, MO = M0 = 48, MTa = M1 = 180.95 (or MNb = M1 = 92.9), MLi = M2 = 6.94.

Table 1 Comparison of phase transition temperatures in both normal [17] and ilmenite-type LiTaO3
Full size table

3 Results and discussion

In principle, we could test these vacancy models by comparing the experimental results with the calculated values according to the theoretical approach previously mentioned. To make the comparison between the three vacancy models, we have used the experimental data of the Curie temperatures and the crystal parameters measured by Bennani and Husson [22] and those used in the Safaryan work [12].

To calculate the Curie temperatures, we need to know the Curie temperature of the exact stoichiometry compositions. The average values of the estimations are \( T_{\text{cTa}} \) = 934 K and \( T_{\text{cNb}} \) = 1480 K [14].

Comparing the experimental data with the theoretically calculated values, one can see a very close agreement between the measured temperatures and the lithium vacancy model values (Fig. 3). The obtained results show clearly that the Curie temperatures of the lithium vacancy model coincide with the experimental values. Consequently, this model shows that the Curie temperature decreases as the composition x increases. It is the first direct quantitative evidence that the lithium vacancies are indeed dominant in nonstoichiometric ilmenite LiTaO3.

Fig. 3
figure 3

Variation of the Curie temperature \( T_{{{\text{c}}\,{\text{Ta}}}}^{*} \) of ilmenite versus nonstoichiometric composition x. The calculated values according to the (a), (b) and (c) vacancy models are compared to the experimental data of Ref. [17]

Full size image

The oxygen and tantalate vacancies do not significantly contribute to the nonstoichiometry in these samples. Table 1 shows the measured Curie temperature and the calculated values of the ilmenite and normal nonstoichiometric LiTaO3 for the lithium vacancy model (c).

To illustrate the defect ilmenite type of the nonstoichiometric LiNbO3, we report in Fig. 4 the Curie temperature \( T_{\text{cNb}}^{*} \) as a function of the composition x. In this figure, we presented the defect structure vacancy models in the same x composition interval. Comparison between calculated values of (a), (b) and (c) models and experimental data is indicated in Fig. 4. As LiNbO3 is isomorphous with LiTaO3, we can deduce that the experimental Curie temperature is calculated from the lithium vacancy model, which confirms the previous results [23].

Fig. 4
figure 4

Variation of the Curie temperature \( T_{{{\text{c}}\,{\text{Nb}}}}^{*} \) of ilmenite versus nonstoichiometric composition x. The calculated values according to the (a), (b) and (c) vacancy models are compared to the experimental data of Ref. [10]

Full size image

The measured Curie temperature and the calculated values of the ilmenite and normal nonstoichiometric LiNbO3 for the lithium vacancy model (c) are shown in Table 2.

Table 2 Comparison of phase transition temperatures in both normal [9] and ilmenite-type LiNbO3
Full size table

The analytical expressions of the Curie temperature of the normal and ilmenite-type LiBO3 (Nb or Ta) are represented in Table 3.

Table 3 The Curie temperature \( T_{\text{cB}}^{ * } \) as a function of the nonstoichiometric composition x of the normal and ilmenite-type LiBO3
Full size table

The lithium vacancy model illustrated in Figs. 3 and 4 exhibits that the agreement between the experimental facts and theoretical predictions is quite satisfactory. The decrease in the Curie temperature can be interpreted in terms of competition between Li+ and Ta5+ ions (Fig. 3), and between Li+ and Nb5+ (Fig. 4). According to the (c) model, the linear increase with the increasing composition x results from an increasing Ta (or Nb) density and a decreasing Li density. The values of the lithium vacancy model are in excellent agreement with experimental data.

It is clear from Tables 1 and 2 that the results obtained by this theoretical approach show that the (c) model in ilmenite-type gives better results than in the normal structure. Furthermore, the ilmenite type is in better agreement than normal structure.

According to the experimental results used, we suggest that the ilmenite type is more dominant than the normal structure.

4 Conclusion

On the experimental measurements of Curie temperature, we have applied the theory of ferroelectric transition on the nonstoichiometric ilmenite-type LiBO3 (B = Ta or Nb). This theoretical result proves the existence of ilmenite-like stacking defect in nonstoichiometric LiBO3. The lithium vacancy model is quantitatively and qualitatively proved as the best model to interpret defect structure in lithium tantalate and lithium niobate. These results are in excellent agreement with the Li vacancy model and show us a new view on the intrinsic defect of LiBO3.

Finally, this approach shows that the ilmenite-type structure is more probable to describe the experiment, particularly the mechanism responsible for substitution.