Cosmological study of particle creation in higher derivative theory

Abstract

In this paper, we have presented accelerated expanding cosmological models with particle creation in flat FRW background within the framework of higher derivative theory. In order to explore the role of particle creation on dynamical parameters, we have considered hybrid, intermediate and emergent forms of scale factor. Further, we have considered the well-accepted values of free parameters to explore the possibility of transition from a decelerated to accelerated period of expansion based on deceleration parameter and effective equation of state. Finally, the effect on state finder parameters $\{r, s\}$, measuring the deviation of the considered models from the concordance model, has also been discussed.

1 Introduction

Cosmology nowadays presents innovative activities because of theoretical developments and more data analysis. Astrophysics performs tests of fundamental theories, and thus in different periods, observations present the study about evolution of the universe with the help of cosmology. Many problems in standard cosmology have been successfully explained by the inflationary universe models [1, 2] which suggest that the universe has undergone a period of rapid expansion where the scale factor increases exponentially [3]. The theoretical development in study of the role of gravity and a number of investigations into quantum theory attracted the attention of researchers in studies of the early universe models [1, 2, 4,5,6,7,8]. The early universe models provide a mechanism to generate small-scale density fluctuations in the universe which needed to seed galaxy formation [7, 8]. Literature survey clearly indicates that in order to explain the cosmological problems of the early universe many alternative theories have also been proposed [9,10,11,12]. To regularise ultraviolet divergences in Einstein theory, generalised Einstein theory [13] with an additional $R^{2}$ term (higher derivative theory) has been introduced. Parting ways from the singularities in the big bang theory, the bouncing models [14,15,16,17,18,19] are being studied in cosmology. Causal viscous cosmological model in higher derivative theory was studied by Paul et al. [20]. In expanding universe, bulk viscous stress has been described phenomenologically in terms of particle production, but in both the cases thermodynamical behaviour of the universe changes. Singh et al. [21] investigated the cosmological model with particle creation during evolution of the universe in the frame work of higher derivative theory of gravity.

The idea of particle production in cosmology has been extensively studied in the literature [22,23,24,25,26,27,28]. The thermodynamics of open system in the reference of cosmology have been studied for the particle production out of gravitational energy. In this context, a new concept of adiabatic transformation has been presented from close to open systems by Prigogine et al. [29]. Irreversible matter production from the gravitational field allows us to consider the universe as an adiabatic open thermodynamic system. In that case, thermodynamic energy conservation equation becomes

$$\begin{aligned} d(\rho V)+p\hbox {d}V-\left( \frac{\rho +p}{n}\right) \hbox {d}N=0, \end{aligned}$$

(1)

where V is the volume of the system, $n=\frac{N}{V}$ is the particle number density, $\rho$ is the energy density, p is the pressure and N is the particle number in V. The conservation equation may be written as,

$$\begin{aligned} d(\rho V)+(p+p_{\mathrm{c}})\hbox {d}V=0. \end{aligned}$$

(2)

The supplementary pressure corresponding to matter creation is denoted by $p_{\mathrm{c}}$ and expressed as,

$$\begin{aligned} p_{\mathrm{c}}=-\left( \frac{\rho +p}{n}\right) \frac{\hbox {d}N}{\hbox {d}V}=-\left( \rho +p\right) \frac{{\dot{N}}}{N} \left( \frac{1}{3H}\right) . \end{aligned}$$

(3)

Depending on the presence or absence of particle production, the creation pressure $p_{\mathrm{c}}$ is negative or zero. The production of new particles is equivalent to adding the supplementary pressure term to the thermodynamic pressure p so that the conservation equation for closed system

$$\begin{aligned} d(\rho V)+p\hbox {d}V=0 \end{aligned}$$

(4)

can be modified to Eq. (2) for an open system. Entropy (S) is proportional to the number of particles included in the system. The increase in entropy for an adiabatic open system is only due to matter creation. So we have the following relation,

$$\begin{aligned} \frac{\hbox {d}S}{S}=\frac{\hbox {d}N}{N}. \end{aligned}$$

(5)

The condition that the only particle number variations admitted are such that $\hbox {d}N\ge 0$ as the second law of thermodynamics requires that $\hbox {d}S\ge 0$. The thermodynamics of particle production in different context have been studied by several authors [30, 31]. Further in open thermodynamic system,

$$\begin{aligned} \frac{{\dot{N}}}{N}=\frac{{\dot{n}}}{n}+\frac{{\dot{V}}}{V}= \frac{{\dot{n}}}{n}+3H=\Gamma \end{aligned}$$

(6)

where $\Gamma$ is the source function. If $\Gamma > 0$, then there is particle production, $\Gamma < 0$ indicates particle annihilation and vanishing $\Gamma$ shows there is no particle production.

By generalising the power law and exponential law, a new form of scale factor called hybrid expansion law [32,33,34] has been studied in the literature. In the context of exact inflationary solutions, one of the interesting scenarios has been obtained by using an exponential potential for inflation, yielding a power-law evolution of the scale factor in cosmic time [35]. Another class of exact solution is for an inverse power-law potential. Here, the inflationary stage can be described by the intermediate inflation model [36, 37]. Intermediate scenario has been extensively studied in the literature [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52].

A model of closed universe with only radiation, having characteristic that asymptotically $(as\ t\rightarrow -\infty )$ approaches to the state of an Einstein static model, was obtained by Harrison [53]. In the past, Ellis and Maartens [54, 55] were able to formulate emergent universe in a model with a minimally coupled scalar field $\phi$ with a special form of self-interacting potential and some ordinary matter with equation of state $p=\gamma \rho$, $(-\frac{1}{3}\le \gamma \le 1)$. Mukherjee et al. [56] obtained solutions for Starobinsky model having properties of an emergent universe. A general framework for an emergent universe using an ad hoc equation of state which has exotic behaviour has been formulated by Mukherjee et al. [57]. In the literature, a lot of work has been done in modelling of emergent universe for many forms of matter as well as for different theories of gravity [58,59,60,61,62,63,64,65].

In the present paper, we are studying particle creation mechanism with the framework of higher derivative theory in flat FRW geometrical background. Recently, a model of emergent universe is formulated using the mechanism of particle creation [66]. The universe is considered as a non-equilibrium thermodynamical system with dissipation due to particle creation in framework of spatially flat FRW space-time with perfect fluid satisfying barotropic equation of state. It would be interesting to study the behaviour of source function $\Gamma$ and energy conditions with different forms of scale factor (namely HEL, IEL and EL) in the higher derivative theory. In this paper, the particle creation for hybrid $(a(t)=t^{b}e^{\beta t})$, intermediate $(a(t)=\hbox {exp}(mt^{n}))$ and emergent $(a(t)=a_{0}(k+\hbox {exp}(ut))^{\nu })$ form of scale factor has been studied. The paper is organised as follows: Sect. 2 deals with the cosmological equations; Sect. 3 investigates the hybrid expansion law (HEL), intermediate expansion law (IEL) and emergent law (EL); Sect. 4 is composed of result and discussion; Sect. 5 concludes the study.

2 Equations of the cosmological model

We consider the following generalised action in order to study classical solutions with particle production,

$$\begin{aligned} I=\int \sqrt{-g}\left[ -\frac{1}{2}(R+\alpha R^{2})+L_{\mathrm{matter}}\right] \hbox {d}^{4}x \end{aligned}$$

(7)

where g is the determinant of the metric tensor $g_{ij}$, G is the gravitational constant, R is the Ricci scalar curvature and $\alpha$ is a positive constant. In this paper, we take $8\pi G=\hbar =k_{\mathrm{B}}=c=1$. From the action, the field equations can be written as,

$$\begin{aligned} R_{ij}-\frac{1}{2}g_{ij}R+\alpha \left[ 2R\left( R_{ij}- \frac{1}{2}g_{ij}R\right) +2(R_{;ij}-g_{ij}\square R)\right] =-T_{ij} \end{aligned}$$

(8)

Where $T_{ij}$ is the energy–momentum tensor for matter distribution defined as,

$$\begin{aligned} T_{ij}=(\rho +p)u_{i}u_{j}-pg_{ij} \end{aligned}$$

(9)

Homogeneous and isotropic flat FLRW metric is given by

$$\begin{aligned} \hbox {d}s^{2}=\hbox {d}t^{2}-a^{2}(t)[\hbox {d}r^{2}+r^{2}(\hbox {d}\theta ^{2}+\sin ^{2}\theta \hbox {d}\phi ^{2})] \end{aligned}$$

(10)

For a spatially flat FLRW metric, field Eq. (8) takes the form

$$\begin{aligned} H^{2}-6\alpha [2H{\ddot{H}}-{\dot{H}}^{2}+6H^{2}{\dot{H}}]=\frac{\rho }{3} \end{aligned}$$

(11)

along with the conservation equation for the matter

$$\begin{aligned} {\dot{\rho }}+3H(p_{\mathrm{eff}}+\rho )=0 \end{aligned}$$

(12)

where $H=\frac{{\dot{a}}}{a}$ is the Hubble parameter and overhead dot denotes derivative with respect to cosmic time t. We consider the universe as an open thermodynamic system with N particles initially. Suppose a random fluctuation in curvature induces a transformation of gravitational energy into matter energy which creates additional number of particles $\hbox {d}N$. Because of increase in the number of particles from N to $N+\hbox {d}N$, a negative supplementary pressure arises with the thermodynamic pressure and the expansion of the universe is driven by this negative pressure. The effective pressure of the cosmic fluid is given by,

$$\begin{aligned} p_{\mathrm{eff}}=p+p_{\mathrm{c}} \end{aligned}$$

(13)

By a ‘barotropic fluid’ we mean some matter or field with pressure p and energy density $\rho$ with equation of state given by

$$\begin{aligned} p=f(\rho ) \end{aligned}$$

(14)

where $\rho$ and p are the energy density and pressure from Eq. (9), respectively. In this paper, we are assuming the barotropic fluid of form

$$\begin{aligned} p=\gamma \rho \end{aligned}$$

(15)

where $\gamma$ is a constant parameter. Cosmic fluid considered may be of normal or exotic form. We define an effective equation of state parameter $\gamma _{\mathrm{eff}}=\frac{p_{\mathrm{eff}}}{\rho }$, which may be used for explanation of the current accelerating scenario of the observable universe. The conservation equation reduces to,

$$\begin{aligned} {\dot{\rho }}+3H(p+\rho )=-3Hp_{\mathrm{c}} \end{aligned}$$

(16)

From Eqs. (15) and (16), we have

$$\begin{aligned} {\dot{\rho }}+3H\rho (1+\gamma )=-3Hp_{\mathrm{c}} \end{aligned}$$

(17)

Using Eqs. (3) and (16), after integration Eq. (17) yields,

$$\begin{aligned} N(t)=N_{0}a^{3}\rho ^{\frac{1}{1+\gamma }} \end{aligned}$$

(18)

where $N_{0}$ is an integration constant. A relation between the particle number density (n) and energy density $(\rho )$ for $\gamma \ne -1$ is given by Eq. (18), and we have

$$\begin{aligned} n\propto \rho ^{\frac{1}{1+\gamma }} \end{aligned}$$

(19)

Gibb’s integrability condition suggests that one cannot independently specify an equation of state for the pressure and temperature [67]. One barotropic relation suggests other barotropic relation, and thus, we have

$$\begin{aligned} T\propto \hbox {exp}\int \frac{\hbox {d}p}{\rho +p(\rho )} \end{aligned}$$

(20)

which with the help of Eq. (15) for $\gamma \ne -1$ gives

$$\begin{aligned} T=T_{0} \rho ^{\frac{\gamma }{1+\gamma }} \end{aligned}$$

(21)

Here, $T_{0}$ is a proportionality constant. From Eqs. (3) and (15), we have $p_{\mathrm{c}}=0$ for $\gamma =-1$. From Eq. (17) with $\gamma =-1$, we observe that there is a critical value of the dark energy density (that is, ${\dot{\rho }}=0$), that is, the energy density becomes constant with $\gamma = -1$. Therefore, cosmic fluid considered may be of normal or exotic form but not vacuum energy. We have to assume one or more physically plausible relation as we have only four independent Eqs., viz. (11), (15), (18) and (21), and five unknown variables, viz. a, $\rho$, p, N and T.

3 Laws of variation of scale factor

3.1 Hybrid expansion law (HEL)

Power-law and exponential law form of scale factor has been extensively studied in the literature and can be generalised as hybrid expansion law [32,33,34, 68, 69]. Akarsu et al. [32] showed that the cosmological parameters related to the current cosmic acceleration of universe for HEL and concordance models are consistent within the $1\sigma$ confidence level. In their work, they have also given the values of some important cosmological parameters with $1\sigma$ errors for models at early and late epochs, showing that they exhibit similar behaviours at late epochs. Recently, hybrid scale factor has been studied to explore the cosmological scenarios of non-minimal matter–geometry coupling in f(R, T) gravity [68, 69]. The universe had undergone to accelerated phase from the decelerated phase [70, 71]. It is interesting to explore the hybrid expansion law in the higher derivative setup with particle creation to predict the decelerated to accelerated regime of cosmic expansion. In order to study particle production during the stages of cosmic evolution, we take the scale factor of the form,

$$\begin{aligned} a(t)=t^{b}e^{\beta t} \end{aligned}$$

(22)

where $b\ge 0$ and $\beta \ge 0$ are some constants. As the special cases, hybrid expansion law mimics power-law form ($a(t)=t^{b}$) for $\beta =0$ and, for $b=0$, exponential law ($a(t)=e^{\beta t}$) form. The expansion tensor ($\Theta _{ij}$) determines the rate of change of distance of neighbouring particles (in our case, cluster of galaxies) in the fluid. The isotropic part of expansion is determined by $\Theta$, the volume expansion, called as expansion scalar. For above form of scale factor, the expansion scalar is given by

$$\begin{aligned} \Theta =3H=\frac{3{\dot{a}}}{a}=\frac{3b}{t}+3\beta \end{aligned}$$

(23)

The deceleration parameter q indicates the rate at which the expansion of universe is slowing down and is given by

$$\begin{aligned} q=-\frac{{\dot{H}}+H^{2}}{H^{2}}=-1+\frac{b}{(b+\beta t)^{2}} \end{aligned}$$

(24)

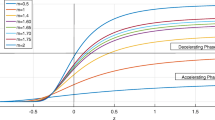
The hybrid expansion law results in a time-dependent deceleration parameter. It is clear that as $t\rightarrow \infty$, $q\rightarrow -1$. The requirement of accelerating universe suggests that $t>\frac{\sqrt{b}-b}{\beta }$ and $b<1$. The behaviour of q with z is given in Fig. 1.

Fig. 1

Variation of q versus z for $\ b=0.3,\ \beta =0.6$

Using Eq. (22) in Eq. (11), we have

$$\begin{aligned} \rho =\frac{3(b+\beta t)^{2}}{t^{2}}-\frac{18\alpha }{t^{4}}\left[ 3b^{2}-6b(b+\beta t)^{2}+4\beta tb\right] \end{aligned}$$

(25)

Fig. 2

Variation of $\rho ,\ p_\mathrm{c}$ and $p_{\mathrm{eff}}$ versus t for $\alpha =0.5,\ b=0.3,\ \beta =0.6$ and $\gamma =0$

Fig. 3

Variation of $\rho ,\ p_\mathrm{c}$ and $p_{\mathrm{eff}}$ versus t for $\alpha =0.5,\ b=0.3,\ \beta =0.6$ and $\gamma =\frac{1}{3}$

From Eq. 25 and Figs. 2 and 3, it is clear that at $t=0$, energy density becomes infinite. It is observed that $\rho \ge 0$ throughout the evolution of the universe. $p_{\mathrm{eff}}$ is negative throughout the evolution of the universe which shows that $p_{\mathrm{c}}$ is negative and it dominates the equilibrium pressure p; hence, the effective pressure $p_{\mathrm{eff}}$ is negative and universe expands with acceleration. The resulting expressions for energy conditions take the form

$$\begin{aligned} \rho -p_{\mathrm{eff}}= & {} -\frac{2b}{t^{4}}\left[ \beta t^{2}-36\alpha (1-\beta t-2b)\right] +2\left[ \frac{3(b+\beta t)^{2}}{t^{2}}-\frac{18\alpha }{t^{4}}\left[ 3b^{2}-6b(b+\beta t)^{2}+4\beta tb\right] \right] \end{aligned}$$

(26)

$$\begin{aligned} \rho +p_{\mathrm{eff}}= & {} \frac{2b}{t^{4}}\left[ \beta t^{2}-36\alpha (1-\beta t-2b)\right] \end{aligned}$$

(27)

$$\begin{aligned} \rho +3p_{\mathrm{eff}}= & {} \frac{6b}{t^{4}}\left[ \beta t^{2}-36\alpha [(1-\beta t-2b)\right] -2\left[ \frac{3(b+\beta t)^{2}}{t^{2}}-\frac{18\alpha }{t^{4}}\left[ 3b^{2}-6b(b+\beta t)^{2}+4\beta tb\right] \right] \end{aligned}$$

(28)

$$\begin{aligned} \gamma _{\mathrm{eff}}= & {} -1+\frac{2b\left[ \beta t^{2}-36\alpha (1-\beta t-2b)\right] }{3(b+\beta t)^{2}t^{2}-18\alpha \left[ b^{2}-6b(b+\beta t)^{2}+4\beta t b\right] } \end{aligned}$$

(29)

Figure 4 shows the variation of $\gamma _{\mathrm{eff}}$ verses cosmic time. It can be seen that $\gamma _{\mathrm{eff}}\rightarrow {-1}$ as $t\rightarrow \infty$. From Fig. 5, it can be seen that $\rho \pm p_{\mathrm{eff}}\ge 0$ and $\rho +3p_{\mathrm{eff}}< 0$ throughout the evolution of the universe. Using the values of a(t) and $\rho (t)$ from Eqs. (22) and (25) in Eq. (18), we get an expression for particle number N(t) as,

$$\begin{aligned} N(t)=N_{1}t^{3b-\frac{4}{(1+\gamma )}}e^{3\beta t}\left[ t^{2}(b+\beta t)^{2}-6\alpha (3b^{2}-6b(b+\beta t)^{2}+4\beta tb)\right] ^{\frac{1}{1+\gamma }} \end{aligned}$$

(30)

where $N_{1}=3^{\frac{1}{1+\gamma }}N_{0}$. Using Eq. (24) in Eq. (20), we get

$$\begin{aligned} T(t)=\frac{T_{1}}{t^{\frac{4\gamma }{1+\gamma }}}\left[ t^{2}(b+\beta t)^{2}-6\alpha (3b^{2}-6b(b+\beta t)^{2}+4\beta tb)\right] ^{\frac{\gamma }{1+\gamma }} \end{aligned}$$

(31)

where T is the temperature in terms of cosmic time t and $T_{1}=3^{\frac{\gamma }{1+\gamma }}T_{0}$. The ratio of potential energy to kinetic energy during expansion of the universe $\Omega =\frac{\rho }{3H^{2}}$ becomes

$$\begin{aligned} \Omega =1-\frac{6\alpha }{t^{2}(b+\beta t)^{2}}\left[ 3b^{2}-6b(b+\beta t)^{2}+4\beta tb \right] \end{aligned}$$

(32)

From Eq. (32) it is clear that as $t\rightarrow \infty$, $\Omega \rightarrow 1$.

Fig. 4

Variation of $\gamma _{\mathrm{eff}}$ versus t for $\alpha =0.5,\ b=0.3$ and $\beta =0.6$

Fig. 5

Variation of $\rho -p_{\mathrm{eff}},\ \rho +p_{\mathrm{eff}}$ and $\rho +3p_{\mathrm{eff}}$ versus t for $\alpha =0.5,\ b=0.3$ and $\beta =0.6$

The cosmological diagnostic pair $\{r,s\}$ called state finder is geometrical parameters and allows us to characterise the property of dark energy in a model in independent manner. For $\Lambda CDM$ model $\{r,s\}=\{1,0\}$. The behaviour of q versus r and s versus r is given in Figs. 6 and 7, respectively.

$$\begin{aligned} r= & {} \frac{\dddot{a}}{aH^{3}}=\frac{2b-(b+\beta t)[3b-(b+\beta t)^{2}]}{(b+\beta t)^{3}} \end{aligned}$$

(33)

$$\begin{aligned} s= & {} \frac{r-1}{3(q-0.5)}=\frac{4b-6b(b+\beta t)}{3(b+\beta t)[2b-3(b+\beta t)^{2}]} \end{aligned}$$

(34)

Fig. 6

Variation of q versus r for $\alpha =0.5,\ b=0.3$

Fig. 7

Variation of s versus r for $\alpha =0.5,\ b=0.3$

3.2 Intermediate expansion law (IEL)

Study of intermediate expansion law in cosmology has been done by John D. Barrow in 1990 [36, 37], where the scale factor gets an exponential function of time as $a(t) = \hbox {exp}(mt^n)$, $m > 0$ and $0< n <1$. This form of scale factor can be acquired from a potential asymptotically looks like negative power but not exactly [38]. Inflationary universe with this form of scale factor expands at a rate intermediate between that of the traditional de Sitter inflation and that of the power-law inflationary models. Intermediate inflation in Einstein gravity creates a scale invariant perturbation when $n = 2/3$ [36, 37]. Intermediate scenario is able to satisfy the bound on scalar spectra index $n_\mathrm{s}$ and tensor-to-scalar ratio r, measured by observation on CMB [39, 40]. There are large number of works in the literature with intermediate expansion law in isotropic and anisotropic metric background [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52] that have been widely debated in different theories of gravity. It will be interesting to study IEL in higher derivative theory with particle creation to understand the behaviour of source function and energy conditions along with the behaviour of deceleration parameter. We consider the scale factor of the form,

$$\begin{aligned} a(t)=\hbox {exp}(mt^{n}) \end{aligned}$$

(35)

where m is a constant and $0<n<1$. The expansion scalar takes the form

$$\begin{aligned} \Theta =3H=\frac{3{\dot{a}}}{a}=3mnt^{n-1} \end{aligned}$$

(36)

Deceleration parameter q for scale factor (35) can be written as,

$$\begin{aligned} q=-\frac{{\dot{H}}+H^{2}}{H^{2}}=-1-\frac{n-1}{mnt^{n}} \end{aligned}$$

(37)

The requirement of accelerating expansion of universe suggests that $n< 1$ and $t> \left( \frac{1-n}{mn}\right) ^{\frac{1}{n}}$.

Fig. 8

Variation of q versus z for $n=0.5, m=0.7$

From Eq. (37), it is clear that q is a decreasing function of time and as $t\rightarrow \infty$, $q\rightarrow -1$. From Fig. 8, it is clear that q undergoes transition from $q>0$ to $q<0$. Using Eq. (35) in Eq. (11), we have

$$\begin{aligned} \rho =3(mn)^{2}t^{2(n-2)}\left[ t^{2}-6\alpha (n-1)(n-3+6mnt^{n})\right] \end{aligned}$$

(38)

Fig. 9

Variation of $\rho ,\ p_\mathrm{c}$ and $p_{\mathrm{eff}}$ versus t for $\alpha =0.5,\ n=0.5,\ m=0.7$ and $\gamma =0$

Fig. 10

Variation of $\rho ,\ p_\mathrm{c}$ and $p_{\mathrm{eff}}$ versus t for $\alpha =0.5,\ n=0.5,\ m=0.7$ and $\gamma =\frac{1}{3}$

From Figs. 9 and 10, it can be seen that $\rho \ge 0$ throughout the evolution of the universe. $p_{\mathrm{eff}}$ is positive at the beginning of the evolution of the universe, but at large times, it is negative. The resulting expressions for energy conditions take the form

$$\begin{aligned} \rho -p_{\mathrm{eff}}= & {} 6(mn)^{2}t^{2(n-2)}\left[ t^{2}-6\alpha (n-1)(n-3+6mnt^{n})\right] -\nonumber \\&\qquad 2mn(n-1)t^{n-4}\left[ t^{2}-6\alpha [(n-2)(n-3+6mnt^{n})+3mn^{2}t^{n}]\right] \end{aligned}$$

(39)

$$\begin{aligned} \rho +p_{\mathrm{eff}}= & {} 2mn(n-1)t^{n-4}\left[ t^{2}-6\alpha [(n-2)(n-3+6mnt^{n})+3mn^{2}t^{n}]\right] \end{aligned}$$

(40)

$$\begin{aligned} \rho +3p_{\mathrm{eff}}= & {} 6mn(n-1)t^{n-4}\left[ t^{2}-6\alpha [(n-2)(n-3+6mnt^{n})+3mn^{2}t^{n}]\right] -\nonumber \\&\qquad 6(mn)^{2}t^{2(n-2)}\left[ t^{2}-6\alpha (n-1)(n-3+6mnt^{n})\right] \end{aligned}$$

(41)

$$\begin{aligned} \gamma _{\mathrm{eff}}= & {} -1+\frac{2(n-1)\left[ t^{2}-6\alpha [(n-2)(n-3+6mnt^{n})+3mn^{2}t^{n}]\right] }{3(mn)t^{n}\left[ t^{2}-6\alpha (n-1)(n-3+6mnt^{n})\right] } \end{aligned}$$

(42)

Fig. 11

Variation of $\gamma _{\mathrm{eff}}$ versus t for $\alpha =0.5,\ n=0.5,\ m=0.7$

Fig. 12

Variation of $\rho -p_{\mathrm{eff}}$, $\rho +p_{\mathrm{eff}}$ and $\rho +3p_{\mathrm{eff}}$ versus t for $\alpha =0.5,\ n=0.5,\ m=0.7$

From Fig. 11, in the beginning of universe $\gamma _{\mathrm{eff}}\ge 0$ but at late times, $\gamma _{\mathrm{eff}}\rightarrow -1$ which is in accordance with recent observations [70,71,72]. From Fig. 12, at the beginning of the universe (for small epoch) $\rho -p_{\mathrm{eff}}<0$, $\rho +p_{\mathrm{eff}}>0$ and $\rho +3p_{\mathrm{eff}}>0$. At late times, $\rho -p_{\mathrm{eff}}>0$, $\rho +p_{\mathrm{eff}}\rightarrow 0$ and $\rho +3p_{\mathrm{eff}}<0$; therefore, consequently, we have $\gamma _{\mathrm{eff}}\rightarrow -1$.

Substituting the values of a(t), $\rho (t)$ from Eqs. (35) and (38) in Eq. (18), we get an expression for particle number N(t) as,

$$\begin{aligned} N(t)=N_{2}e^{3mt^{n}}t^{\frac{2(n-2)}{1+\gamma }}\left[ t^{2}-6\alpha (n-1)(n-3+6mnt^{n})\right] ^{\frac{1}{1+\gamma }} \end{aligned}$$

(43)

where $N_{2}=[3m^2n^{2}]^{\frac{1}{1+\gamma }}N_{0}$. From Eq. (38), Eq. (21) can be written as,

$$\begin{aligned} T(t)=T_{2}t^{\frac{2\gamma (n-2)}{1+\gamma }}\left[ t^{2}-6\alpha (n-1)(n-3+6mnt^{n})\right] ^{\frac{\gamma }{1+\gamma }} \end{aligned}$$

(44)

where $T_{2}=[3(mn)^{2}]^{\frac{\gamma }{1+\gamma }}T_{0}$. The ratio of potential energy to kinetic energy during expansion of the universe $\Omega =\frac{\rho }{3H^{2}}$ becomes

$$\begin{aligned} \Omega =1-6\alpha t^{-2}(n-1)(n-3+6mnt^{n}) \end{aligned}$$

(45)

From Eq. (45), it can be seen that at large times, i.e. as $t\rightarrow \infty$, $\Omega \rightarrow 1$. The state finder parameters r and s for the present model can be written as,

$$\begin{aligned} r= & {} \frac{\dddot{a}}{aH^{3}}=\frac{(n-1)[(n-2)+2mnt^{n}]+mnt^{n}[(n-1)+ mnt^{2}]}{(mn)^2t^{2n}} \end{aligned}$$

(46)

$$\begin{aligned} s= & {} \frac{r-1}{3(q-0.5)}=\frac{2(n-1)[(n-2)+3mnt^{n}]}{3mn[6(1-n)-3mnt^{n}]} \end{aligned}$$

(47)

The graphs of q versus r and s versus r are given in Figs. 13 and 14, respectively.

Fig. 13

Variation of q versus r for $n=0.5$

Fig. 14

Variation of s versus r for $n=0.5$

3.3 Emergent law (EL)

The scale factor satisfying emergent law (EL) is given as,

$$\begin{aligned} a(t)=a_{0}(k+e^{ut})^{\nu } \end{aligned}$$

(48)

where $k>0$, $a_{0}>0$, $u>0$ and $\nu >0$ are some constants. In the literature, a lot of works have been done in modelling of emergent universe for different types of matter in general relativity and in other theories of gravity as well [58,59,60,61,62,63,64,65]. By considering the universe as a non-equilibrium thermodynamical system with dissipation due to particle creation in framework of spatially flat FRW space-time with perfect fluid satisfying barotropic equation of state, a model of emergent universe is formulated using the mechanism of particle creation by S. Chakraborty [66]. The thermodynamical aspects of homogeneous and isotropic model of universe with dissipative phenomena related to effective bulk viscous pressure have been investigated by Bhandari et al. [73]. It would be interesting to study emergent law behaviour in the framework of higher derivative theory with particle creation in flat FRW background. The expansion scalar takes the form

$$\begin{aligned} \Theta =3H=3\frac{u\nu e^{ut}}{k+e^{ut}} \end{aligned}$$

(49)

The deceleration parameter q is given by

$$\begin{aligned} q=-1-\frac{k}{\nu e^{ut}} \end{aligned}$$

(50)

The emergent law results in a time-dependent deceleration parameter. As $t\rightarrow \infty$, $q\rightarrow -1$. From Fig. 15, we have an accelerating model of universe with emergent law form of scale factor.

Fig. 15

Variation of q versus z for $k=1,\ u=\frac{\sqrt{3}}{2},\ \nu =\frac{2}{3}$

Using Eq. (48) in Eq. (11), we have

$$\begin{aligned} \rho =\frac{3u^{2}\nu ^{2}e^{2ut}}{(k+e^{ut})^{4}}\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] \end{aligned}$$

(51)

Fig. 16

Variation of $\rho ,\ p_\mathrm{c}$ and $p_{\mathrm{eff}}$ versus t for $k=1,\ u=\frac{\sqrt{3}}{2},\ \nu =\frac{2}{3}$ and $\gamma =0$

Fig. 17

Variation of $\rho ,\ p_\mathrm{c}$ and $p_{\mathrm{eff}}$ versus t for $k=1,\ u=\frac{\sqrt{3}}{2},\ \nu =\frac{2}{3}$ and $\gamma =\frac{1}{3}$

From Figs. 16 and 17, it is clear that at the beginning of the universe energy density, creation pressure and effective pressure are negative and all are positive at late times. The resulting expressions for energy conditions take the form

$$\begin{aligned} \rho -p_{\mathrm{eff}}= & {} \frac{6u^{2}\nu ^{2}e^{2ut}}{(k+e^{ut})^{4}}\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] +\frac{2u}{(k+e^{ut})^{3}}\nonumber \\&\qquad \left[ (k-2e^{ut})\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] +e^{ut}(k+e^{ut})\left[ k+e^{ut}+6\alpha u^{2}(1-3\nu )\right] \right] \end{aligned}$$

(52)

$$\begin{aligned} \rho +p_{\mathrm{eff}}= & {} -\frac{2u(k-2e^{ut})}{(k+e^{ut})^{3}}\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] \nonumber \\&\qquad -\frac{2ue^{ut}}{(k+e^{ut})^{2}}\left[ k+e^{ut}+6\alpha u^{2}(1-3\nu )\right] \end{aligned}$$

(53)

$$\begin{aligned} \rho +3p_{\mathrm{eff}}= & {} -\frac{6u^{2}\nu ^{2}e^{2ut}}{(k+e^{ut})^{4}}\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] -\frac{6u}{(k+e^{ut})^{3}}\nonumber \\&\qquad \left[ (k-2e^{ut})\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] +e^{ut}(k+e^{ut})\left[ k+e^{ut}+6\alpha u^{2}(1-3\nu )\right] \right] \end{aligned}$$

(54)

The expression for $\gamma _{\mathrm{eff}}$ in the case of emergent expansion is given by

$$\begin{aligned} \gamma _{\mathrm{eff}}=\frac{N}{D}-1 \end{aligned}$$

(55)

where $N=2(k+e^{ut})\left[ (k-2e^{ut})\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] +e^{ut}(k+e^{ut})\left[ k+e^{ut}+6\alpha u^{2}(1-3\nu )\right] \right]$ and $D=3uv^{2}e^{2ut}\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right]$.

Fig. 18

Variation of $\gamma _{\mathrm{eff}}$ versus t for $k=1,\ u=\frac{\sqrt{3}}{2}$ and $\nu =\frac{2}{3}$

Fig. 19

Variation of $\rho -p_{\mathrm{eff}},\ \rho +p_{\mathrm{eff}}$ and $\rho +3p_{\mathrm{eff}}$ versus t for $k=1,\ u=\frac{\sqrt{3}}{2}$ and $\nu =\frac{2}{3}$

From Fig. 18, it is interesting to note that $\gamma _{\mathrm{eff}}\ge 0$ at the late times of evolution of the universe. From Fig. 19, one can be observe that $\rho - p_{\mathrm{eff}}\ge 0$ throughout the evolution of the universe, whereas $\rho +p_{\mathrm{eff}}$ and $\rho +3p_{\mathrm{eff}}$ are negative at the beginning of the universe and both are positive at late times.

Using the values of a(t) and $\rho (t)$ from Eq (48) and (51) in Eq (18), we get an expression for particle number N(t) as,

$$\begin{aligned} N(t)=N_{3}\ e^{\frac{2ut}{1+\gamma }}(k+e^{ut})^{3\nu -\frac{1}{4(1+\gamma )}}\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] ^{\frac{1}{1+\gamma }} \end{aligned}$$

(56)

where $N_{3}=N_{0}a_{0}^3(3u^2\nu ^2)^{\frac{1}{1+\gamma }}$. Using Eq. (51) in Eq. (20), we get

$$\begin{aligned} T(t)=T_{3}\left[ \frac{e^{2ut}}{(k+e^{ut})^{4}}\right] ^{\frac{\gamma }{1+\gamma }}\left[ (k+e^{ut})^{2}-6\alpha ku^{2}[k-2e^{ut}(1-3\nu )]\right] ^{\frac{\gamma }{1+\gamma }} \end{aligned}$$

(57)

where T is the temperature at cosmic time t and $T_{3}=T_{0}(3u^2\nu ^2)^{\frac{\gamma }{1+\gamma }}$. The ratio of potential energy to kinetic energy during expansion of the universe $\Omega =\frac{\rho }{3H^{2}}$ becomes

$$\begin{aligned} \Omega =1-\frac{6\alpha ku^{2}}{(k+e^{ut})^{2}}\left[ k-2e^{ut}(1-3\nu )\right] \end{aligned}$$

(58)

From Eq. (58), it is clear that as $t\rightarrow \infty$, $\Omega \rightarrow 1$. The cosmological diagnostic pair $\{r,s\}$ for the present model is given by

$$\begin{aligned} r= & {} \frac{\dddot{a}}{aH^3}=\frac{(k+\nu e^{ut})[k+e^{ut}(\nu -1)]}{\nu ^2 e^{2ut}} \end{aligned}$$

(59)

$$\begin{aligned} s= & {} \frac{r-1}{3(q-0.5)}=\frac{-2k(k+2\nu e^{ut})+2e^{ut}(k+\nu e^{ut})}{3\nu e^{ut}(2k+3\nu e^{ut})} \end{aligned}$$

(60)

The behaviour of q versus r and s versus r is given in Figs. 20 and 21, respectively.

Fig. 20

Variation of q versus r for $k=1$, $\nu =\frac{2}{3}$

Fig. 21

Variation of s versus r for $k=1$, $\nu =\frac{2}{3}$

Fig. 22

Variation of Source function versus t for HEL, IEL and EL

4 Results and discussions

The general expression for standard point-wise conditions for energy–momentum tensor of form $T_{ij}=(\rho +p)u_{i}u_{j}-pg_{ij}$ is as follows [74,75,76]

Null energy condition $(\hbox {NEC}) \Leftrightarrow \rho + p\ge 0$

Weak energy condition $(\hbox {WEC}) \Leftrightarrow \rho \ge 0,\ \rho + p\ge 0$

Dominant energy condition $(\hbox {DEC}) \Leftrightarrow \rho \ge 0,\ \rho \pm p\ge 0$

Strong energy condition $(\hbox {SEC}) \Leftrightarrow \rho + 3p\ge 0,\ \rho + p\ge 0$

Violation of NEC will violate other energy conditions as well.

For HEL, $\rho \ge 0$, $\rho \pm p_{\mathrm{eff}}\ge 0$ and $\rho +3p_{\mathrm{eff}}< 0$. So NEC, WEC and DEC are satisfied and SEC is violated throughout the evolution of the universe for the considered HEL model in higher derivative theory with particle creation. As $t\rightarrow \infty$ (that is, $z\rightarrow -1$), $q\rightarrow -1$. The negative values of q describe the acceleration of universe model. From Fig. 1, the model has a transition from deceleration to acceleration at $z_{tr}=0.3989$. The requirement of accelerating universe in terms of cosmic time suggests that $t>\frac{\sqrt{b}-b}{\beta }$ and $b<1$. Also, as the time passes, we have $\gamma _{\mathrm{eff}}\rightarrow -1$ (see Fig. 4) in accordance with recent observational data on cosmic microwave background radiation fluctuations [72]. For HEL model, source function ($\Gamma$) is positive throughout the evolution of the universe, and as time evolves, it shows a nearly constant behaviour (see Fig. 22).

For IEL, we have $\rho \ge 0$, and at late times, $\rho \rightarrow 0$. At the beginning of the universe $\rho -p_{\mathrm{eff}}<0$, $\rho +p_{\mathrm{eff}}>0$ and $\rho +3p_{\mathrm{eff}}>0$. At large times, model satisfies the NEC, WEC and DEC and violates the SEC. The accelerated regime of expansion is considered to be a late time phenomenon. IEL model is also having transition into an accelerating phase from decelerating phase, but it requires constraint on n as $n< 1$ and will accelerate for $t>(\frac{1-n}{mn})^{\frac{1}{n}}$. From Fig. 8, we observe that deceleration parameter q changes its behaviour at $z_{tr}=-0.6329$. From Fig. 11, we observe that $\gamma _{\mathrm{eff}}\rightarrow -1$ at late times. For IEL, $\Gamma$ is a decreasing function of time (in beginning of universe evolution), and at late times, it is having almost constant behaviour (see Fig. 22).

It can be observed from the Raychaudhuri Eq. (61) that for accelerated expansion of the universe [70,71,72], $(\rho +3p_{\mathrm{eff}})$ (where $\rho +3p_{\mathrm{eff}}$ for different forms of scale factors is given in Eqs. 28, 41 and 54) has to be negative. Negative value of $(\rho +3p_{\mathrm{eff}})$ (in other words, $\gamma _{\mathrm{eff}}<-\frac{1}{3}$) results in violation of SEC, and as $t\rightarrow \infty$, we have $\gamma _{\mathrm{eff}}\rightarrow -1$ (see Figs. 4, 11).

$$\begin{aligned} \frac{\ddot{a}}{a}=-\frac{1}{6}(\rho +3p_{\mathrm{eff}}) \end{aligned}$$

(61)

For EL, we note that $\rho <0$ at the beginning of the universe and at late times $\rho >0$ and is close to 1. $\rho -p_{\mathrm{eff}}\ge 0$ throughout the evolution of the universe, whereas $\rho +p_{\mathrm{eff}}$ and $\rho +3p_{\mathrm{eff}}$ are negative at the beginning of the universe and positive at late times. So EL model satisfies NEC, WEC, DEC and SEC at late times, whereas it violates all the energy conditions at the beginning of the universe. EL model has always $q<-1$, and as $t\rightarrow \infty$, $q\rightarrow -1$. For EL, initially $\Gamma$ is negative, and at late times, it is positive and asymptotically close to zero (see Fig. 22). It is interesting to note that for emergent scale factor in higher derivative theory with particle creation mechanism, at late times all energy conditions are satisfied.

5 Conclusions

In this paper, the flat FRW model in higher derivative theory with particle production has been investigated. we have considered hybrid expansion law, intermediate law and emergent law for variation of scale factor. In standard model of cosmology, a negative pressure fluid is exactly the mechanism responsible for accelerated phase of universe expansion. Particle creation mechanism in the considered modified gravity model (higher derivative theory) allows us to understand the particle production annihilation in the considered expansion laws for the universe.

HEL and IEL scale factor undergoes transition from decelerated phase to accelerated phase of evolution in the higher derivative theory model with particle creation, perhaps due to overall effect of matter and geometry which are responsible for the form of $\gamma _{\mathrm{eff}}$. In both HEL and IEL models, at late times, we have $\gamma _{\mathrm{eff}}\rightarrow -1$ which is in accordance with recent observational data [70,71,72] which explains the current phase of accelerated expansion. Behaviour of source function ($\Gamma$) with respect to cosmic time gives idea about particle production, particle annihilation and no particle production. If $\Gamma >0$ there is particle production, $\Gamma <0$ indicates particle annihilation and vanishing $\Gamma$ shows there is no particle production. HEL and IEL models have $\Gamma > 0$ during the evolution, although at late times $\Gamma$ shows almost constant behaviour. Therefore, HEL and IEL models both are capable of explaining the current phase of expansion with particle production taking place throughout the evolution phase.

For EL model, deceleration parameter (q) is an increasing function of time and $q\rightarrow -1$ as $t\rightarrow \infty$. Energy density ($\rho$) is positive and increases with time. EL model satisfies NEC, WEC, DEC and SEC at late times and violates all the energy conditions at the beginning of the universe. As $t\rightarrow 0$, EL model evolves with particle annihilation, but after some time it shows particle production during the evolution of the universe. It is noted that the emergent scenario is a consequence of particle creation process [66]. In higher derivative theory framework of $f(R)=R+\alpha R^2$ with particle creation mechanism, the emergent scenario evolving with $q\rightarrow -1$ asymptotically is satisfying $\rho +3p_{\mathrm{eff}}>0$ and having almost zero particle production at late times.