1 Introduction

In recent years there are considerable efforts to characterize properties of the quantum entropy. In particular, these efforts have been focused on the entropy of the Jaynes–Cummings model [1,2,3,4,5,6]. The authors in [1, 2] have shown that von Neumann entropy is a very useful operational measure of the purity of the quantum state, which automatically includes all moments of the density operator. The time evolution of the field (atomic) entropy reflects the time evolution of the degree of entanglement between the atom and the field. The higher the entropy, the greater the entanglement. Furthermore, much attention have been focused on the generalization and the extension for the original Jaynes–Cummings model [7,8,9,10,11,12,13,14]. Also, many authors focus their attention to investigation the evolution of the (atomic) field entropy for the three-level atom one-mode [15,16,17,18,19,20,21,22,23] and two-mode [24]. The generalizations have included three-level atom interacting within various forms of the intensity-dependent coupling functional [25,26,27,28,29,30]. Finally, the system of a four-level atom interacting with a single-mode of electromagnetic field [31,32,33,34,35] and a two-mode has been studied [36].

For an N-type atom, the atom has two upper levels and two lower levels which are linked through a linear interaction. When the fields successively connect the dipole-transition channels in an N-type four-level atom, the optical properties are controlled by three-photon coherence in the N-type scheme the conjoint action of two competitive two-photon coherences (arising from the upper- and lower-level doublets) is responsible for obtaining the quantum-optical effects [37]. By controlling the competitive two-photon coherences, one can optimize the atomic response in a variety of conditions.

Recently, lot of attentions has been paid to the N-type four-level in the literature. For instance, it has frequently been demonstrated as a model for observing pressure-induced resonances [38]. Also, Doppler-free resonance is observed in the N-type system [39]. Moreover, quantum coherence effects of an inner transition in the four-level N-type atom have been investigated [40]. Also, it can be found in experimental works with gases of alkali-earth atoms which aim at optical frequency standards [41] or at reaching the quantum degeneracy regime by all-optical means [42]. A nondegenerate four-level N-type scheme was experimentally implemented to observe electromagnetically induced transparency or electromagnetically induced absorption [43,44,45]. In addition, this kind of atomic structure has been proposed for the generation of ultraviolet laser gain through the laser without inversion method [46]. Furthermore, the use of the four-level N-type schemes of resonance transitions, for which Zeeman coherence can be spontaneously transferred from the excited to the ground level [47], opens up new opportunities for studying nonlinear phenomena. Such a scheme was investigated both theoretically [48] and experimentally [49, 50].

It is worth mentioning that, the nonlinear properties of nonlinear interaction models are of great interest [51,52,53,54] because of there applications in the fields of two-mode two-photon micromaser [55, 56], photonic band gap systems [57,58,59] and photonic gate implementation [60]. The strong coupling between some levels of the atomic system and some selected modes of quantized elastic or electromagnetic field would result in these nonlinear interactions. Constructing an effective Hamiltonian which contains the essential ingredients of the physical situation and solvable may be considered as a starting point. Extended Jaynes–Cummings models to describe trapped atoms have been constructed and arbitrary atom-field coupling could be tailored at well [61, 62]. Accordingly, we particularly choose N-configuration for the four-level atom interacting with a single-mode field including acceptable kinds of nonlinearities of both the field and the intensity-dependent atom-field coupling in this paper.

The phenomenon of collapses and revivals represents one of the most important nonclassical phenomena in the field of quantum optics. The observation of this phenomenon occurred during the course of interaction between the field and the atom within a cavity. This phenomenon is a pure quantum mechanical effect and having its origin in the granular structure of the photon-number distribution of the initial field [63]. The collapse–revival phenomenon has been seen in nonlinear optics for the single-mode mean-photon number of the Kerr nonlinear coupler [64] when the modes are initially prepared in coherent light, however, in this case the origin of the occurrence of such a phenomenon is in the presence of nonlinearity in the system (third-order nonlinearity specified by the cubic susceptibility).

On the other hand, there has been tremendous progress in the ability to generate experimentally states of the electromagnetic field with manifestly quantum or nonclassical characteristics [65,66,67,68,69,70]. Squeezed states of light are nonclassical states for which the fluctuations in one of the two quadrature phase amplitudes of the electromagnetic field drop below the level of fluctuations associated with the vacuum state of the field. Squeezed states therefore provide a field which is in some sense quieter than the vacuum state and hence can be employed to improve measurements precision beyond the standard quantum limits. The squeezed coherent state \(|\alpha ,r\rangle\) may be generated from the vacuum state \(|0\rangle\) by the squeezing operator S(r)\(=\exp {[\frac{1}{2}z^{*}{a}-\frac{1}{2}z{a}^{\dag }]}\) and the coherent displacement operator \(D{(\alpha )}=\exp {(\alpha {a}^{\dag }-\alpha ^{*}{a})}\) in the form [67, 69, 71]

$$\begin{aligned} |\alpha ,r\rangle =D{(\alpha )}S{(r)}|0\rangle \end{aligned}$$
(1)

with the photon number distribution given by

$$\begin{aligned} |P^{(n)}|^{2}=\frac{(\tanh r)^{n}}{2^{n}n!\cosh r}\left| H_{n}\left( \frac{\varepsilon }{\sqrt{2\cosh r\sinh r}}\right) \right| ^{2}\exp \left[ -|\varepsilon |^{2}+\tanh r\quad Re(\varepsilon )^{2}\right] \end{aligned}$$
(2)

where \(z=r\exp {i\phi }\), and \(\phi\) is taken to be zero here \(\quad \varepsilon =\alpha \cosh r +\alpha ^{*}\sinh r,\quad \alpha =|\alpha |\exp (i\varsigma )\) and \(H_{n}\) is the Hermite polynomial. We suppose here the minor axis of the ellipse, representing the direction of squeezing, parallel to the coordinate of the field oscillator. The initial phase \(\varsigma\) of \(\alpha\) is the angle between the direction of coherent excitation and the direction of squeezing. The mean photon number of this field is equal to \({\bar{n}}=|\alpha |^{2}+\sinh ^{2}r\). When \(r=0\) one gets the photon distribution for the coherent state, whereas for \(\alpha =0\) the photon distribution of the squeezed vacuum state is recovered. The latter distribution is oscillatory with zeros for odd n. The variance for this state is given by Var(n)\(=|\alpha |^{2}(\cosh {2r}-\sinh {2r}\cos {\varsigma })+\frac{1}{2}\sinh ^{2}{2r}\).

Here, we aim at extending the previously cited treatments to study the problem of a four-level atom in N-configuration interacting with a single-mode field including acceptable kinds of nonlinearities of both the field and the intensity-dependent atom-field coupling. It differs from [30] in structure of the physical system, the nature of the states of the field and the detailed structure of the entropy. Also, collapse–revival phenomenon through the relation (\(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\)) is considered here. Our goal is to examine the influences of the mean photon number, the field nonlinearity (Kerr-like medium), detuning and the different intensity-dependent coupling functionals on both the degree of entanglement through linear entropy and collapse–revival phenomenon through the relation (\(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\)).

2 The model

The total Hamiltonian of the system in the rotating wave approximation is of the form \((\hbar =1)\):

$$\begin{aligned} H=H_{0}+H_{int}, \end{aligned}$$
(3)

where

$$\begin{aligned} H_{0}=\Omega {\hat{a}}^{+}{\hat{a}}+\sum \limits _{j=1}^{4}\omega _{j}\sigma _{j,j}, \end{aligned}$$
(4)

where \(\omega _{1}\), \(\omega _{2}\), \(\omega _{3}\), and \(\omega _{4}\) are the atomic levels energies \(|1\rangle\), \(|2\rangle\), \(|3\rangle\), and \(|4\rangle\) respectively in which \((\omega _{1}>\omega _{2}>\omega _{3}>\omega _{4})\), the operators \({\hat{a}}^{+}\), and \({\hat{a}}\) are boson operators of the field and they obey the commutation relation \([{\hat{a}},{\hat{a}}^{+} ]=I\) where I is the unity operator. The operator \(\sigma _{jj}\) is \(j\mathrm{th}\) level occupation operator and defined by \(\sigma _{jj}=|j\rangle \langle j|\).

The interaction Hamiltonian of the N-configuration four-level atom is given by:-

$$\begin{aligned} H_{int}&= {} {\mathfrak{R}}({\hat{a}}^{\dagger }{\hat{a}}) +\lambda _{1}(\sigma _{13}f_{1}({\hat{a}}^{\dagger }{\hat{a}}){\hat{a}} +h.c.)\nonumber \\&\quad+ \lambda _{2}(\sigma _{23}f_{2}({\hat{a}}^{\dagger }{\hat{a}}){\hat{a}} +h.c.)+\lambda _{3}(\sigma _{24}f_{3}({\hat{a}}^{\dagger }{\hat{a}}){\hat{a}} +h.c.). \end{aligned}$$
(5)

where \(\lambda _{i}f_{i}({\hat{a}}^{\dagger }{\hat{a}})\) represents an arbitrary intensity-dependent atom-field coupling with the detuning parameters (Fig. 1)

$$\begin{aligned} \Delta _{1}=-\Omega +(\omega _{1}-\omega _{3}),\quad \Delta _{2}=-\Omega +(\omega _{2}-\omega _{3}),\quad \Delta _{3}=-\Omega -(\omega _{2}-\omega _{4}). \end{aligned}$$
(6)
Fig. 1
figure 1

Schematic structure of the N-configuration of a four-level atom interacting with a single-mode cavity field with detuning parameters \(\Delta _{1},\Delta _{2}\) and \(\Delta _{3}\)

Full size image

The initial state \(\left| \Psi _{AF}(0)\right\rangle\) of the combined atom-field system may be written as:

$$\begin{aligned} \left| \Psi _{AF}(0)\right\rangle =\left| \Psi _{A}(0)\right\rangle \otimes \left| \Psi _{F}(0) \right\rangle . \end{aligned}$$
(7)

Where \(\left| \Psi _{A}(0)\right\rangle =\left| 1 \right\rangle\) the initial state of the atom being in the upper most excited state and \(\left| \Psi _{F}(0)\right\rangle =|\theta \rangle\) is the initial state of the field. The initial state \(|\theta \rangle =\sum \nolimits _{n=0} P^{(n)}|n\rangle\) where the probability amplitude \(P^{(n)}\) is defined in the usual manner as \(P^{(n)}=\langle n|\theta \rangle\). The time evolution of the atom-field system is defined by the unitary evolution operator U(t) generated by H. Thus U(t) is given by

$$\begin{aligned}U(t)\equiv \exp \left( -iHt\right) . \end{aligned}$$

The unitary evolution operator U(t) can be written as:

$$\begin{aligned} U(t)= & {} \exp {(-i\omega _{3}t)} |0,3\rangle \langle 0,3|+\exp {(-i\omega _{4}t)} |0,4\rangle \langle 0,4| \nonumber \\&+\,\exp {(-it\Upsilon ^{\left( n\right) }_{j})}|\psi ^{(n)}_{j}\rangle \langle \psi ^{(n)}_{j}|. \end{aligned}$$
(8)

Where \(|0,3\rangle\), \(|0,4\rangle\) and \(|\psi ^{(n)}_{j}\rangle\) \((j=1,2,3\) and 4) are the dressed states of the Hamiltonian H in Eq. (3) associated respectively with the eigenvalues \(\omega _{3}\), \(\omega _{4}\), and \(\Upsilon ^{(n)}_{j}\) with

$$\begin{aligned} |\psi ^{(n)}_{j}\rangle= & {} \mu ^{(n)}_{j}|n,1\rangle +\nu ^{(n)}_{j} |n,2\rangle +\xi ^{(n)}_{j}|n+1,3\rangle +\upsilon ^{(n)}_{j}|n+1,4\rangle . \end{aligned}$$
(9)

The coefficients \(\mu ^{(n)}_{j}\), \(\nu ^{(n)}_{j}\), \(\xi ^{(n)}_{j}\), and \(\upsilon ^{(n)}_{j}\) of the dressed states \(|\psi ^{(n)}_{j}\rangle\) are given by:-

$$\begin{aligned} \left( \begin{array}{c} \mu ^{(n)}_{j}\\ \nu ^{(n)}_{j}\\ \xi ^{(n)}_{j} \\ \upsilon ^{(n)}_{j} \end{array}\right) =\frac{1}{\varpi }\left( \begin{array}{c} V_{1}V_{2}^{2}(\Gamma _{4}-\Upsilon ^{(n)}_{j})\\ V_{2}(\Gamma _{4}-\Upsilon ^{(n)}_{j})L_{j}(n)\\ -L_{j}(n)K_{j}(n)\\ -V_{2}V_{3}L_{j}(n) \end{array} \right) \end{aligned}$$
(10)

where

$$\begin{aligned} \varpi ^{2}= & {} V_{1}^{2}V_{2}^{4}(\Gamma _{4}-\Upsilon ^{(n)}_{j})^{2}+ V_{2}^{2}(\Gamma _{4}-\Upsilon ^{(n)}_{j})^{2}L^{2}_{j}(n)+L^{2}_{j}(n)K^{2}_{j}(n)+V^{2}_{2}V^{2}_{3}L^{2}_{j}(n) \end{aligned}$$
(11)

with

$$\begin{aligned} L_{j}(n)= & \,{} (\Gamma _{1}-\Upsilon ^{(n)}_{j})(\Gamma _{3}-\Upsilon ^{(n)}_{j})-V_{1}^{2},\nonumber \\ K_{j}(n)= &\,\,{} (\Gamma _{2}-\Upsilon ^{(n)}_{j})(\Gamma _{4}-\Upsilon ^{(n)}_{j})-V_{3}^{2},\nonumber \\ \Gamma _{1}= &\,\,{} \omega _{1}+\Omega n+{\mathfrak{R}}(n),\nonumber \\ \Gamma _{2}= &\,\,{} \omega _{2}+\Omega n+{\mathfrak{R}}(n),\nonumber \\ \Gamma _{3}= &\,\,{} \omega _{3}+\Omega (n+1)+{\mathfrak{R}}(n+1),\nonumber \\ \Gamma _{4}= &\,\,{} \omega _{4}+\Omega (n+1)+{\mathfrak{R}}(n+1),\nonumber \\ V_{i}= &\,\,{} \lambda _{i}f_{i}(n)\sqrt{n+1},\quad \quad \quad \quad \quad (i=1,2,3) \end{aligned}$$
(12)

while, the eigenvalues \(\Upsilon _{j}^{(n)}\) (\(j=1, 2, 3\), and 4) of the Hamiltonian are the four real roots of the following equation

$$\begin{aligned} \left[ \Upsilon ^{(n)}_{j}\right] ^{4}+Q_{1}\left[ \Upsilon ^{(n)}_{j}\right] ^{3}+Q_{2}\left[ \Upsilon ^{(n)}_{j}\right] ^{2}+Q_{3}\Upsilon ^{(n)}_{j}+Q_{4}=0, \end{aligned}$$
(13)

after minor algebra and by using Ferri’s method [72] we have

$$\begin{aligned} \Upsilon ^{(n)}_{1, 2}=-\frac{Q_{1}}{4}+\frac{1}{2}\left( \sqrt{ 2y^{(n)}-\beta _{1}}\right) \pm \frac{1}{2}\sqrt{(2y^{(n)}-\beta _{1})-4\left( y^{(n)} +\frac{\beta _{2}}{2\sqrt{{(2y^{(n)}-\beta _{1})}}}\right) },\nonumber \\ \Upsilon ^{(n)}_{3,4}=-\frac{Q_{1}}{4}-\frac{1}{2}\left( \sqrt{ 2y^{(n)}-\beta _{1}}\right) \pm \frac{1}{2}\sqrt{(2y^{(n)}-\beta _{1})-4\left( y^{(n)} -\frac{\beta _{2}}{2\sqrt{{(2y^{(n)}-\beta _{1})}}}\right) }, \end{aligned}$$
(14)

where the parameter \(y^{(n)}\) is one of the real roots of the equation

$$\begin{aligned} \left[ y^{(n)}\right] ^{3}-\left( \frac{\beta _{1}}{2}\right) \left[ y^{(n)}\right] ^{2}-\beta _{3} y^{(n)} +\frac{4\beta _{1}\beta _{3}-\beta _{2}^{2}}{8}=0, \end{aligned}$$
(15)

where

$$\begin{aligned} \beta _{1}= &\,\,{} Q_{2}-\frac{3}{8}Q^{2}_{1}\nonumber \\ \beta _{2}= &\,\,{} Q_{3}-\frac{1}{2}Q_{1}Q_{2}+\frac{1}{8}Q^{3}_{1}\nonumber \\ \beta _{3}= &\,\,{} Q_{4}-\frac{1}{4}Q_{1}Q_{3}+\frac{1}{16}Q_{2}Q^{2}_{1}-\frac{3}{256}Q^{4}_{1} \end{aligned}$$
(16)

while

$$\begin{aligned} Q_{1}= &\,\,{} -(\Gamma _{1}+\Gamma _{2}+\Gamma _{3}+\Gamma _{4}),\nonumber \\ Q_{2}= &\,\,{} \Gamma _{1}\Gamma _{2}+\Gamma _{1}\Gamma _{3}+\Gamma _{1}\Gamma _{4}+\Gamma _{2}\Gamma _{3}+\Gamma _{2}\Gamma _{4}+\Gamma _{3}\Gamma _{4}-V^{2}_{1}-V^{2}_{2}-V^{2}_{3},\nonumber \\ Q_{3}= &\,\,{} V^{2}_{1}(\Gamma _{2}+\Gamma _{4})+V^{2}_{2}(\Gamma _{1}+\Gamma _{4})+V^{2}_{3}(\Gamma _{1}+\Gamma _{3}),\nonumber \\&\,\,-\,\Gamma _{1}\Gamma _{2}(\Gamma _{3}+\Gamma _{4})-\Gamma _{3}\Gamma _{4}(\Gamma _{1}+\Gamma _{2}) ,\nonumber \\ Q_{4}= &\,\,{} \Gamma _{1}\Gamma _{2}\Gamma _{3}\Gamma _{4}+V^{2}_{1}V^{2}_{3}-\Gamma _{2}\Gamma _{4}V^{2}_{1}-\Gamma _{1}\Gamma _{4}V^{2}_{2}-\Gamma _{1}\Gamma _{3}V^{2}_{3}. \end{aligned}$$
(17)

3 Linear entropy (LE)

Linear entropy can be regarded as the lowest-order approximation to the von Neumann entropy and a good criterion to understand the purity loss of the quantum system. Also, linear entropy is a direct and simple measure of the degree of entanglement between the subsystem. Furthermore, it is an useful quantity to understand the degree of decoherence (coherence loss) [73]. The parameter measured linear entropy has been introduced as [74]

$$\begin{aligned} LE(t)=Tr\left[ \rho _{A}(t)(1-\rho _{A}(t))\right] =Tr \rho _{A}(t)-Tr \rho ^{2}_{A}(t)=1-Tr \rho ^{2}_{A}(t) \end{aligned}$$
(18)

where \(\rho _{A}(t)\) is the atomic density operator. Furthermore, Eq. (18) indicates that, the linear entropy can range between zero, corresponding to a completely pure state, (i.e., \(\rho _{A}(t)=\rho ^{2}_{A}(t))\) and \([1-(1/\hbox {the dimension of the density matrix})]\), corresponding to a completely mixed state. Consequently, the nonzero values of this indicator show the impurity of the state of the system. Also, it may be noted that, maximal entanglement as well as the most mixed state appears whenever the idempotent defect reaches a value of 3/4.

Having obtained the explicit form of the unitary operator U(t) in Sect. 2, we are therefore, in a position to discuss the linear entropy of the system. To achieve that we use Eqs. (7) and (8, 9) to obtain the density operator \(\rho (t)\) of the system at any time \(t>0\) as:

$$\begin{aligned} \rho (t)= & {} |\Psi _{AF}(t)\rangle \langle \Psi _{AF}(t)| =U(t)|\Psi _{AF}(0)\rangle \langle \Psi _{AF}(0)|U^{+}(t), \end{aligned}$$
(19)

Then the atomic reduced density matrix \(\rho _{A}(t)\) at any time \(t>0\) can be given as

$$\begin{aligned} \rho _{A}(t)=Tr_{F} & \rho (t)= \left( \begin{array}{cccc} \rho _{11} &{} \rho _{12} &{} \rho _{13} &{} \rho _{14}\\ \rho _{21} &{} \rho _{22} &{} \rho _{23} &{} \rho _{24}\\ \rho _{31} &{} \rho _{32} &{} \rho _{33} &{} \rho _{34}\\ \rho _{41} &{} \rho _{42} &{} \rho _{43} &{} \rho _{44} \end{array} \right) \end{aligned}$$
(20)

where the elements of atomic reduced density matrix \(\rho _{A}(t)\) in Eq. (20) are given as

$$\begin{aligned} \rho _{11}= & {} \sum \limits _{n=0}|P^{(n)}|^{2}\left| \Lambda {(n,t)}\right| ^{2},\quad \quad \quad \quad \quad \quad \quad \rho _{22}=\sum \limits _{n=0}|P^{(n)}|^{2}\left| \Xi {(n,t)}\right| ^{2},\nonumber \\ \rho _{33}= & {} \sum \limits _{n=0}|P^{(n)}|^{2}\left| \Theta {(n,t)}\right| ^{2},\quad \quad \quad \quad \quad \quad \quad \rho _{44}=\sum \limits _{n=0}|P^{(n)}|^{2}\left| \Phi {(n,t)}\right| ^{2},\nonumber \\ \rho _{12}= & {} \rho ^{*}_{21}=\sum \limits _{n=0}|P^{(n)}|^{2}\Lambda {(n,t)}\Xi ^{*}{(n,t)},\quad \quad \rho _{13}=\sum \limits _{n=1}P^{(n)}P^{*(n-1)}\Lambda {(n,t)}\Theta ^{*}{(n-1,t)},\nonumber \\ \rho _{14}= & {} \sum \limits _{n=1}P^{(n)}P^{*(n-1)}\Lambda {(n,t)}\Phi ^{*}{(n-1,t)},\quad \rho _{23}=\sum \limits _{n=1}P^{(n)}P^{*(n-1)}\Xi {(n,t)}\Theta ^{*}{(n-1,t)},\nonumber \\ \rho _{24}= & {} \sum \limits _{n=1}P^{(n)}P^{*(n-1)}\Xi {(n,t)}\Phi ^{*}{(n-1,t)},\quad \rho _{31}=\sum \limits _{n=0}P^{(n)}P^{*(n+1)}\Theta {(n,t)}\Lambda ^{*}{(n+1,t)},\nonumber \\ \rho _{32}= & {} \sum \limits _{n=0}P^{(n)}P^{*(n+1)}\Theta {(n,t)}\Xi ^{*}{(n+1,t)},\quad \rho _{34}=\rho ^{*}_{43}=\sum \limits _{n=0}|P^{(n)}|^{2}\Theta {(n,t)}\Phi ^{*}{(n,t)},\nonumber \\ \rho _{41}= & {} \sum \limits _{n=0}P^{(n)}P^{*(n+1)}\Phi {(n,t)}\Lambda ^{*}{(n+1,t)},\quad \rho _{42}=\sum \limits _{n=0}P^{(n)}P^{*(n+1)}\Phi {(n,t)}\Xi ^{*}{(n+1,t)}, \end{aligned}$$
(21)

With

$$\begin{aligned} \Lambda (n,t)= & {} \sum \limits _{j=1}^{3}\exp (-it\Upsilon ^{(n)}_{j}) \mu ^{(n)}_{j}\mu ^{*(n)}_{j}, \Xi (n,t)=\sum \limits _{j=1}^{3}\exp (-it\Upsilon ^{(n)}_{j}) \nu ^{(n)}_{j}\mu ^{*(n)}_{j},\nonumber \\ \Theta (n,t)= & {} \sum \limits _{j=1}^{3}\exp (-it\Upsilon ^{(n)}_{j}) \xi ^{(n)}_{j}\mu ^{*(n)}_{j}, \Phi (n,t)=\sum \limits _{j=1}^{3}\exp (-it\Upsilon ^{(n)}_{j}) \upsilon ^{(n)}_{j}\mu ^{*(n)}_{j}. \end{aligned}$$
(22)

Where \(\mu ^{(n)}_{j}\), \(\nu ^{(n)}_{j}\), \(\xi ^{(n)}_{j}\) and \(\upsilon ^{(n)}_{j}\) given in Eq. (10).

Furthermore, by using Eqs. (18) and (20) we get the calculation formalism of the linear entropy as

$$\begin{aligned} LE&= {} 1-(\rho _{11}^{2}+\rho _{22}^{2}+\rho _{33}^{2}+\rho _{44}^{2})\nonumber \\&\quad-\,2(\rho _{12}\rho _{21}+\rho _{13}\rho _{31}+\rho _{14}\rho _{41}+\rho _{23}\rho _{32}+\rho _{24}\rho _{42}+\rho _{34}\rho _{43}) \end{aligned}$$
(23)

By using the above results, we discuss the dynamical behavior of the linear entropy of the present model. In fact the entropy attains the zero value (i.e., disentanglement) when the atom is in one of its pure states while strong entanglement occurs when the inversion is equal to zero. Generally, we observe that the linear entropy satisfies the inequality (\(0 \le LE \le 0.75\)) in all considered cases. To study the effects of the mean photon number, detuning, Kerr-like medium and the intensity-dependent coupling functional on the linear entropy we have plotted the linear entropy function (LE) against the scaled time for different values of parameters.

In Fig. 2(a) when smaller values of the mean photon number parameter are considered, the linear entropy function LE oscillates with oscillations of small frequencies and small amplitudes. It is clear that, increasing the mean photon number not only decreases the maximum and minimum values of the linear entropy but also the number of fluctuations and the amplitude of the atomic entropy are decreased as the mean photon number increases. This in addition to more regular fluctuations with some interference between patterns are observed as long as the values of the mean photon number increases [compare frame(a) with frame(b) in Fig. 2]. Also, it is remarked that the first maximum of the field entropy at t > 0 is achieved at the collapse time, and at one-half of the revival time (the revival time that depends on average photon number), the entropy reaches its local minimum and the average photon number oscillates near the initial value. Also, at the beginning as well as the end of the collapse region, the function LE reaches a maximum value in which the system represented a stronger entangled state, while the smaller entanglement degree observed at mid of the collapse time. (compare frame(a) with frame(b) in Fig. 2). When the detuning parameters \(\Delta _{1},\Delta _{2}\) and \(\Delta _{3}\) take place the linear entropy is strongly affected. Added detuning parameters causes a decrease in the maxima of the atomic entropy function, affects the minima of the atomic entropy function by bringing them upward and causes an elongation in the revivals times [compare Fig. 3 with Fig. 2(b)]. Also, the period of collapses increase and the number of fluctuations decrease until it disappear at large values of the detuning parameters [see Fig. 3(b)]. While, the situation is completely changed when the nonlinearity is modeled by \({\mathfrak{R}}(n)=\chi n(n-1)\) (where \(\chi\) is the dispersive part of the third-order nonlinearity of the Kerr-like medium) is considered. There are sharp peaks observed with some kind of periodicity and the collapse–revival phenomenon in the average photon number becomes less and less prominent as \(\chi\) increases. Also, the maxima and minima of the atomic entropy function begins to decrease, until the pure states occur in a periodical and a regular manner in the first stage of the time evolution, immediately after the onset of the interaction between the field and the atom. While as the time goes on, the atomic entropy function starts to rise to its maximum values [compare Fig. 4 with Fig. 2(b)].

Fig. 2
figure 2

Evolution of the LE as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\chi =0,\Delta _{1}=\Delta _{2}=\Delta _{3}=0, f_{i}(n)=1,\varsigma =0\) and (a) \(r=1,\alpha =1\), (b) \(r=1.7 ,\alpha =\sqrt{20}\)

Full size image
Fig. 3
figure 3

Evolution of the LE as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\chi =0,f_{i}(n)=1,r=1.7 ,\alpha =\sqrt{20},\varsigma =0\) and (a) \(\Delta _{1}=3 , \Delta _{2}=5 ,\Delta _{3}=5\), (b) \(\Delta _{1}=30 , \Delta _{2}=30 ,\Delta _{3}=30\)

Full size image
Fig. 4
figure 4

Evolution of the LE as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\Delta _{1}=\Delta _{2}=\Delta _{3}=0,r=1.7 ,\alpha =\sqrt{20}, f_{i}(n)=1,\varsigma =0\) and (a) \(\chi =0.1\), (b) \(\chi =0.8\)

Full size image
Fig. 5
figure 5

Evolution of the LE as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\Delta _{1}=\Delta _{2}=\Delta _{3}=0,\chi =0,r=1.7 ,\alpha =\sqrt{20},\varsigma =0\) and (a) \(f_{i}(n)=\sqrt{n+1}\), (b) \(f_{i}(n)=1/{\sqrt{n+1}}\)

Full size image

On the other hand, the linear entropy is largely affected by the form of the intensity-dependent coupling functional \(f_{i}(n)\). Here we choose two forms of intenisty dependent coupling functional (i.e \(f_{i}(n)=\sqrt{n+1}\) and \(f_{i}(n)=1/\sqrt{n+1}\) ) to get strong and weak field respectively. When we take \(f_{i}(n)=\sqrt{n+1}\) then \(V_{i}\) in Eq. (12) becomes depended on \((n+1)^2\) instead of \((n+1)\) in case of \(f_{i}(n)=1\), hence Rabi oscillation is largest and we note that the atomic entropy oscillate in irregular manner and the time period becomes very smaller. Also, the minimum values of the atomic entropy becomes smaller than that for \(f_{i}(n)=1\), while the maximum values of the atomic entropy almost not changed. [compare Fig. 5(a) with Fig. 2(b)]. An interesting phenomenon emerges when we consider \(f_{i}(n)=1/\sqrt{n+1}\) where in this case \(V_{i}\) in Eq. (12) and Rabi oscillation are smallest and independent of n. Hence large number of oscillations appear in the evolution of the atomic entropy. Moreover, the atomic entropy function exhibits pure states for a short time after that rises to its maximum values in a rapid manner see Fig. 5(b). Also, the maximum values of the the atomic entropy very smaller comparing with the case in which we take \(f_{i}(n)=1\) [compare Fig. 5(b) and Fig. 3(b)]. At last, we can say that the behavior of the atomic entropy can be controlled by choosing the forms of intensity-dependent coupling functional. Finally, It should be mentioned that these results in all considered cases are agree with that results observed in two and three-level atom systems [1,2,3,4,5,6, 26, 28].

4 Collapse–revival phenomenon

Having obtained the density operator \(\rho (t)\) of the system, therefore we are in a position to calculate the expectation values of the operators \(({\hat{a}}^{\dagger }{\hat{a}})\) which can be used to discuss some statistical properties of the system.

$$\begin{aligned} \left\langle {\hat{a}}^{\dagger }{\hat{a}}\right\rangle =Tr\left( {\hat{a}}^{\dagger }{\hat{a}}\rho (t)\right) ={\bar{n}}+\rho _{33}+\rho _{44} \end{aligned}$$
(24)

then

$$\begin{aligned} \left\langle {\hat{a}}^{\dagger }{\hat{a}}\right\rangle -{\bar{n}}=\rho _{33}+\rho _{44} \end{aligned}$$
(25)

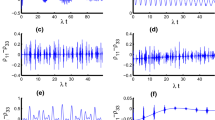
Based on the above observations, we look for the collapse–revival phenomenon in the photon number, we present some interesting numerical results for different parameters to demonstrate the effect on the time evolution of \(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\). Figure (6) show that the time evolution of \(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\) either exhibits periodical oscillations or exhibits collapses and revivals periods. The periodical oscillations are seen very well with the lower values of the mean photon number parameter [see Fig. 6(a)]. On the contrary, the collapses and revivals periods are seen obviously with the higher values of the mean photon number parameter [see Fig. 6(b)]. In Fig. 7 we observe that, the increase in the value of the detuning parameter leads the evolution of the photon number to exhibit what the so-called collapse–revival phenomenon appears and makes the revivals times elongate [compare Fig. 7 with Fig. 6(b)]. the effectiveness of the detuning parameter is confined to a slight shrinking in the amplitudes of the oscillations and a decrease in the maximum values of the evolution of \(\langle {\hat{a}}^{+} {\hat{a}} \rangle -{\bar{n}}\). On the other hand, the Kerr-like parameter causes a reintroduction for the collapse–revival phenomenon and decreases both the maximum values and the revivals times [compare Fig. 6 and Fig. 8]. One of characteristics of the effect of the detuning than the Kerr-like medium is that the first elongates the revivals times while, the second decreases them (compare Fig. 8 with Fig. 7). The increase in the value of the Kerr-like medium parameters leads to a decrease in the maximum values of the evolution of \(\langle {\hat{a}}^{+} {\hat{a}} \rangle -{\bar{n}}\) and the collapse–revival phenomenon becomes less and less prominent. Moreover, There are sharp peaks observed with some kind of periodicity in the evolution of \(\langle {\hat{a}}^{+} {\hat{a}} \rangle -{\bar{n}}\). An interesting phenomenon emerges when the intensity-dependent coupling functional \(f_{i}(n)\) is considered. We note that, in all input cases the behavior of the evolution of \(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\) is nearly similar to the behavior of the atomic entropy function. The played roles by the inputs of the field in the evolution of \(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\) are as their roles in the evolution of the atomic entropy function (compare Fig. 9 and Fig. 5).

Fig. 6
figure 6

Evolution of the \(\langle {\hat{a}}^{\dagger }{\hat{a}}\rangle -{\bar{n}}\) as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\chi =0,\Delta _{1}=\Delta _{2}=\Delta _{3}=0, f_{i}(n)=1,\varsigma =0\) and (a) \(r=1 ,\alpha =1\), (b) \(r=1.7 ,\alpha =\sqrt{20}\)

Full size image
Fig. 7
figure 7

Evolution of the \(\langle {\hat{a}}^{\dagger }{\hat{a}}\rangle -{\bar{n}}\) as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\chi =0,r=1.7 ,\alpha =\sqrt{20}, f_{i}(n)=1,\varsigma =0\) and (a) \(\Delta _{1}=5 , \Delta _{2}=5 ,\Delta _{3}=5\), (b) \(\Delta _{1}=30 , \Delta _{2}=30 ,\Delta _{3}=30\)

Full size image
Fig. 8
figure 8

Evolution of the \(\langle {\hat{a}}^{\dagger }{\hat{a}}\rangle -{\bar{n}}\) as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\Delta _{1}=\Delta _{2}=\Delta _{3}=0,\chi =0,r=1.7 ,\alpha =\sqrt{20}, f_{i}(n)=1,\varsigma =0\) and (a) \(\chi =0.1\), (b) \(\chi =0.8\)

Full size image
Fig. 9
figure 9

Evolution of the \(\langle {\hat{a}}^{\dagger }{\hat{a}}\rangle -{\bar{n}}\) as function of the scaled time \(\lambda t\) with \(\lambda _{i}=\lambda =1,\Delta _{1}=\Delta _{2}=\Delta _{3}=0,\chi =0,r=1.7 ,\alpha =\sqrt{20}, f_{i}(n)=1,\varsigma =0\) and (a) \(f_{i}(n)=\sqrt{n+1}\), (b) \(f_{i}(n)={1}/{\sqrt{n+1}}\)

Full size image

5 Conclusion

We have investigated the evolution of the atomic entropy and the collapse–revival phenomenon through the relation (\(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\)) in a system of \(\mathbf N\)-configuration of the four-level atom, interacting with a single-mode field in a cavity. We take explicitly into account the existence of forms of nonlinearities of both the field and the intensity-dependent atom-field coupling functional when the input field being initially in squeezed coherent states. Generally, we observed that increasing the mean photon number leads to decreasing the atomic entropy. Also, the degree of entanglement between the atom and the field can be controlled by choosing the right forms of intensity-dependent coupling functional \(f_{i}(n)\). Detuning parameters affect the maximum values of the atomic entropy by bringing them down, elongating the revival time and increasing the collapse period. While, the effect of the Kerr medium changes the quasi period of the field entropy evolution and add some regularity to the behavior of the atomic entropy. The Kerr-like medium and detuning have similar effects on the the atomic entropy, where they decrease the maximum values of the atomic entropy. However, they have opposite effects, where the detuning effect increases the revival period the Kerr effect decreases it. At very strong nonlinear interaction of the Kerr-like medium with the field mode, results in that the field and the atom are almost decoupled, hence pure states occur. On the other hand, the time evolution of \(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\) either exhibits periodical oscillations or exhibits collapses and revivals periods. the collapses and revivals periods are seen obviously with the higher values of the mean photon number parameter. One of characteristics of the effect of the detuning than the Kerr-like medium is that the first elongates the revivals times while, the second decreases them. The played roles by the inputs of the field in the evolution of \(\langle {\hat{a}}^{+}{\hat{a}} \rangle -{\bar{n}}\) are as their roles in the evolution of the atomic entropy function.