1 Introduction

New low-dimensional semiconductor structures such as quantum dots (QDs), antidots and pseudodot have recently been paid a great deal of theoretical and experimental attentions [1,2,3,4,5,6], because their various interesting physical phenomena and great potential application values in nano-technology. In recently years, many researchers [7,8,9,10] have studied the physical properties of new quantum structures from the aspects of electron properties, optical properties, phonon effects and polaron effects. Among the studies, the electronic properties have attracted wide attentions because they are important and meaningful for the applications in electronic and optical quantum devices. For example, Madhav et al. [11] examined the electronic properties of anisotropic QDs with magnetic field. It is known that the external factors including temperature, impurity field, electric and magnetic fields, and pressure [12] all change the nanostructures’ electronic properties. Among the above factors, electric field in low-dimensional quantum systems is one of the most important factors for both fundamental views and theoretical points. Recently, some researchers haves studied the low-dimensional systems’ electronic properties under the electric field. Chang et al. [13] investigated the effects of the electric field in the spherical QD. On basis of electronic properties in the QDs, we exactly solved the related Hamiltonian and gave the electron energy levels and wave functions. The two-energy-level system can behave as a qubit, which plays an important role in quantum information processing and computation. Many investigators have studied the interesting qubit in solid semiconductor material. Li et al. [14] calculated the qubit of single-electron in InAs/GaAs QD and indicated that the electron density oscillates on the superposition state in the QD with a period of femtoseconds order. By employing the linear combination operator and unitary transformation methods, Alain Jervé et al. [15] studied the effects of temperature and electric field, the influence of polaron radius and polar angle on the lifetime and energy levels. Tiotsop et al. [16] derived the relations between the polaron life time, the probability density, the Coulomb binding parameter and the polar angle. Using the variational method of Pekar type (VMTP), Tiotsop and Fotue et al. [17] also studied the effects of Shannon entropy and electric field on the polaron in the RbCl triangular quantum dot. To obtain more information about qubit of low-dimensional semiconductor material, the reader is referred to [18,19,20,21,22]. Xiao [23] studied the influence of magnetic field on qubit in the RbCl QPD. Ma et al. [24] investigated the qubit in the RbCl QPD with Coulomb impurity potential and found several methods of prolonging the life of qubit. Sun et al. [25] studied the qubit’s phonon effect. The influence of electric field on the RbCl QPD, however, has not been investigated, which is the motivation of our manuscript. In the present paper, based on the VMPT, we investigate the effects of electric field on the properties of the electron RbCl QPD qubit.

2 Theoretical models

An electron is confined in a RbCl QPD crystal with pseudoharmonic potential and interacts with bulk LO phonons. In the presence of an electric field \(F\) along the \(\rho_{x}\) direction with \(\rho_{x} = r\left( {r,\theta ,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right)\), the system’s Hamiltonian is in the following form [20].

$$H = \frac{{p^{2} }}{2m} + V\left( r \right) + \sum\limits_{{\mathbf{q}}} {\hbar \omega_{LO} } a_{{\mathbf{q}}}^{ + } a_{{\mathbf{q}}} + \sum\limits_{{\mathbf{q}}} {\left[ {V_{q} a_{{\mathbf{q}}} \exp \left( {i{\mathbf{q}} \cdot {\mathbf{r}}} \right) + h.c} \right]} - e^{ * } F\rho_{x} ,$$
(1)

where

$$V\left( r \right) = V_{0} \left( {\frac{r}{{r_{0} }} - \frac{{r_{0} }}{r}} \right)^{2} ,$$
(2)

where \(m\) is the band mass of the electron, \(a_{{\mathbf{q}}}^{ + } \left( {a_{{\mathbf{q}}} } \right)\) denotes the creation (annihilation) operator of the bulk LO phonon with wave vector \({\mathbf{q}}\); \({\mathbf{p}}\) and \({\mathbf{r = }}\left( {{\varvec{\uprho}},z} \right)\) are the momentum and the position vector of the electron. \(V\left( r \right)\) is the pseudoharmonic potential [26] that includes both harmonic QD potential and antidot potential, \(V_{0}\) is the chemical potential of the two-dimensional electron gas and \(r_{0}\) is the zero point of the pseudoharmonic potential.

Following the VMPT [27, 28], the trial ground- and first-excited-states (GFES) wavefunctions may be given as [24, 25].

$$\left| {\varphi_{0} \left( {\lambda_{0} } \right)} \right\rangle = \left| 0 \right\rangle \left| {0_{ph} } \right\rangle = \pi^{{ - \frac{3}{4}}} \lambda_{0}^{{\frac{3}{2}}} \exp \left[ { - \frac{{\lambda_{0}^{2} r^{2} }}{2}} \right]\left| {0_{ph} } \right\rangle ,$$
(3)
$$\left| {\varphi_{1} \left( {\lambda_{1} } \right)} \right\rangle = \left| 1 \right\rangle \left| {0_{ph} } \right\rangle = \left( {\frac{{\pi^{3} }}{4}} \right)^{{ - \frac{1}{4}}} \lambda_{1}^{{\frac{5}{2}}} r\cos \theta \exp \left( { - \frac{{\lambda_{1}^{2} r^{2} }}{2}} \right)\exp \left( { \pm i\phi } \right)\left| {0_{ph} } \right\rangle ,$$
(4)

where \(\lambda_{0}\) and \(\lambda_{1}\) are the variational parameters. \(\left| {0_{ph} } \right\rangle\) represents the phonon’s vacuum state with \(a_{{\mathbf{q}}} \left| {0_{ph} } \right\rangle = 0\). The GFES energies are calculated as follows:

$$E_{0} \left( {\lambda_{0} } \right) = \frac{{3\hbar^{2} }}{4m}\lambda_{0}^{2} + \frac{{3V_{0} }}{{2\lambda_{0}^{2} r_{0}^{2} }} + 2V_{0} \lambda_{0}^{2} r_{0}^{2} - 2V_{0} - \frac{\sqrt 2 }{\sqrt \pi }\alpha \hbar \omega_{LO} \lambda_{0} R_{0} - \frac{{\sqrt \pi e^{ * } }}{{2\lambda_{0} }}F,$$
(5)
$$E_{1} \left( {\lambda_{1} } \right) = \frac{{5\hbar^{2} }}{4m}\lambda_{1}^{2} + \frac{{5V_{0} }}{{2\lambda_{1}^{2} r_{0}^{2} }} + \frac{2}{3}V_{0} \lambda_{1}^{2} r_{0}^{2} - 2V_{0} - \frac{3\sqrt 2 }{4\sqrt \pi }\alpha \hbar \omega_{LO} \lambda_{1} R_{0} - \frac{{\sqrt \pi e^{ * } }}{{2\lambda_{1} }}F,$$
(6)

where \(R_{0} = \left( {{\hbar \mathord{\left/ {\vphantom {\hbar {2m\omega_{LO} }}} \right. \kern-0pt} {2m\omega_{LO} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}\) is the polaron radius. A single qubit is realized in this quantum system. The forms of superposition state are written as:

$$\left| {\psi_{01} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| 0 \right\rangle + \left| 1 \right\rangle } \right).$$
(7)

The time evolution of Eq. (7) can be calculated using

$$\psi_{01} \left( {r,t} \right) = \frac{1}{\sqrt 2 }\psi_{0} \left( r \right)\exp \left( { - \frac{{iE_{0} t}}{\hbar }} \right) + \frac{1}{\sqrt 2 }\psi_{1} \left( r \right)\exp \left( { - \frac{{iE_{1} t}}{\hbar }} \right).$$
(8)

The electron probability density in the RbCl QPD is obtained as

$$Q\left( {r,t} \right) = \left| {\psi_{01} \left( {r,t} \right)} \right|^{2} .$$
(9)

The oscillating frequency of the probability density is calculated as follows

$$f = \frac{{E_{1} - E_{0} }}{h}.$$
(10)

3 Numerical calculation and results discussion

The effective mass of RbCl crystal is taken as \(0.432m_{0}\), the electron–phonon coupling constant is \(\alpha = 3.81\) and the bulk LO phonon energy is \(\hbar \omega_{LO} = 21.639\,{\text{meV}}\) [29]. The numerical calculation results are demonstrated in Figs. 1, 2.

Fig. 1
figure 1

The probability density \(Q\left( {r,t} \right)\) versus the time \(t\) and the electric field \(F\)

Full size image
Fig. 2
figure 2

The oscillating frequency \(f\) versus the electric field \(F\) and the chemical potential of the two-dimensional electron gas \({\text{V}}_{0}\)

Full size image

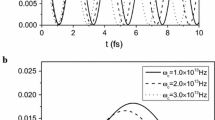
Figure 1 depicts the electron probability density \(Q\) varying with time \(t\) and electric field \(F\) for \({\text{V}}_{0} = 10.0\,{\text{meV}}\), \({\text{R}}_{0} = 0.5\,{\text{nm}}\) and \({\text{r}}_{0} = 1.0\,{\text{nm}}\). The lines of solid, dash, dot and dash dot correspond to the electric field F = 1.0 × 104, 2.0 × 104, 4.0 × 104 and 6.0 × 104 V/cm, respectively. From Fig. 1, we find that the probability density changes with time in the RbCl QPD with a certain period, which agrees with the result in the Refs. [23,24,25]. From Fig. 1, one can also find that the electron probability density is a lifting function of the electric field and the peak value of the probability density decreases with increasing electric field and the peak value appears in the every certain period. The presence of the electric field that equals to introduce another confinement to the electron, which will lead to greater overlapping of electron wavefunction. Consequently, the electron probability density increases with increasing electric field. This result is similar to the case of quantum rod qubit obtained in Ref. [27] at higher temperature regime, whereas at lower temperature regime the result is reversed.

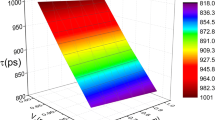
Figure 2 shows oscillating frequency \(f\) as a function of the electric field \(F\) and the two-dimensional electron gas chemical potential \({\text{V}}_{0}\) for \({\text{R}}_{0} = 1.0\,{\text{nm}}\) and \({\text{r}}_{0} = 1.5\,{\text{nm}}\). The oscillating frequency increases with increasing electric field. The influence of the electric field on the first-excited state is stronger than that on the ground state in the RbCl QPD. Moreover, with enhancing electric field, its influence on the first-excited state is not as great as that on the ground-state. As a result, the energy spacing between GFES raises with enhancing electric field, and then the oscillation frequency raises accordingly. Since energy spacing between GFES increases, the oscillating frequency enhances as the two-dimensional electron gas chemical potential increases.

Figures 1, 2 show that the electron probability density and the oscillating frequency increase with increasing electric field, The another reason is that the raising electric field increases the energy of the electron, leading to augmentations of the electron’s lifetime on the superposition state and the oscillating frequency.

The quantum coherence plays a crucial role in the quantum computation and quantum computation, where the electron probability density, the oscillating frequency and the coherence time are the physical quantities representing the properties of coherence. Figures 1, 2 denote the relation between the electron probability density and the oscillating frequency change with the electric field. Here one can see that we can control the probability density and the oscillating frequency by varying the electric field. Therefore, the life time of qubit can be changed, suggesting a new way of suppressing the decoherence. We allow the QPD system to work in higher electric field to increase the probability density and the oscillating frequency. In Fig. 2, we also plot the oscillating frequency versus the two-dimensional electron gas chemical potential, suggesting another way of adjusting oscillating frequency by tuning two-dimensional electron gas chemical potential. We allow the QPD system to have larger two-dimensional electron gas chemical potential to enhance the oscillating frequency. The study of qubit properties in the RbCl QPD is extremely important for prolonging the qubit life time and implement of decoherence suppression in the quantum computation field.

4 Conclusions

Under an applied electric field in the RbCl QPD crystal, we investigate the evolutions of probability density versus the electric field, the time and the dependences of oscillating frequency versus the electric field and two-dimensional electron gas chemical potential by using VMPT. The results indicate that the electron probability density oscillates in the RbCl QPD with a certain period. The electron probability density is an increasing function of electric field. The oscillating frequency increases with increasing electric field and the two-dimensional electron gas chemical potential. The results confirm that the electric field and the two-dimensional electron gas chemical potential are two important factors in investigating the RbCl QPD qubit characteristics.