1 Introduction

In the field of gamma-ray spectrometry with high-purity germanium (HPGe) detectors, applied to measurements of activity when the sample is small and has low radioactivity, the well-type HPGe detectors are widely used. The calculation of absolute activities of natural and artificial radionuclides by gamma spectrometry requires reliable and accurate determination of the detector full-energy peak efficiency [1]. The main problem of the measurements in the well-type detector geometry is the presence of high coincidence summing effects in the case of multi-photon-emitting radionuclides. True coincidence summing effects occur when two or more photons emitted subsequently in the same disintegration act interact in the detector in a time interval smaller than the time required by the detection chain to produce separate signals. In this case, a single global signal is produced, instead of a number of signals, associated each with a specific photon [2]. In the case of extended sources, particularly for small volume sources inside 4π γ-counting detector, the situation is difficult, because to evaluate the coincidence summing correction factors, it is necessary to know the spatial dependence of the detector efficiencies within the detector volume. Moreover, the coincidence effects are high for source–detector close geometries [3]. Ignoring these effects inside a well-type detector can lead to an error of a typical factor of two in the determination of 60Co and 88Y activity, which is used in the calibration process.

In the current work, an aqueous cylindrical radioactive source (1 ml), filled by 70 % of its total volume, is used to calibrate a well-type HPGe detector (p-type). The total, full-energy peak efficiency values and the coincidence correction factors have been calculated using numerical integration and efficiency transfer method (ET) such as applied successfully before for different source-to-detector systems [4–14].

2 Mathematical preview

The efficiency transfer technique (ET) as presented in [10] has been applied to establish the efficiency calibration curves of well-type detectors based on the following equation:

$$ \varepsilon_{\text{target}} = \frac{{\varOmega_{\text{target}} }}{{\varOmega_{\text{ref}} }}\varepsilon_{\text{ref}} $$
(1)

where ε target and ε ref are the full-energy peak efficiencies of the target (a volume source measured inside the detector well) and the reference geometry (an isotropic radiating axial point source measured out of the detector well), respectively. While Ω target and Ω ref are the effective solid angles subtended by the detector surface with the volume and the reference geometry sources, respectively. In order to use the efficiency transfer technique (ET), the experimental reference efficiency, ε ref, has been measured [7].

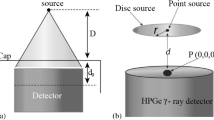
The effective solid angle, Ω Eff (Point-Out), in which the source is located outside the well-type detector, can be calculated according to five probabilities for the photon to enter the detector covering distances, d 1, d 2, d 3, d 4 and d 5 as shown in Fig. 1(a)–1(c) Considering a well-type detector of outer radius, R, internal radius, R 1, base height, L, and depth, L 1, the photon path distances can be expressed as follows:

Fig. 1
figure 1

Schematic diagram of a well-type detector using an axial point source measured out the detector cavity with possible different pass lengths: (a) for \( \theta_{1}^{{\prime }} \le \theta_{1} < \theta_{2}^{{\prime }} , \) (b) \( {\text{for }}\theta_{1} < \theta_{1}^{{\prime }} < \theta_{2}^{{\prime }} \) and (c) for \( \theta_{1}^{{\prime }} < \theta_{2}^{{\prime }} < \theta_{1} \)

Full size image
  1. 1.

    The photon may enter through base-1 and exit through base-2 of the detector, travelling distance, d 1, given by:

    $$ d_{1} = \frac{L}{\cos \theta }-\frac{{L_{1} }}{\cos \theta }$$
    (2)
  2. 2.

    The photon may enter through side-1 and exit through base-2 of the detector, travelling distance, d 2, given by:

    $$ d_{2} = \frac{L}{\cos \theta }-\left( {\frac{{R_{1} }}{\sin \theta }-\frac{h}{\cos \theta }} \right) $$
    (3)
  3. 3.

    The photon may enter through base-1 and exit through side-2 of the detector, travelling distance, d 3, given by:

    $$ d_{3} = \left( {\frac{R}{\sin \theta }-\frac{h}{\cos \theta }} \right)-\frac{{L_{1} }}{\cos \theta } $$
    (4)
  4. 4.

    The photon may enter through side-1 and exit through side-2 of the detector, travelling distance, d 4, given by:

    $$ d_{4} = \left( {\frac{R}{\sin \theta }-\frac{{R_{1} }}{\sin \theta }} \right) $$
    (5)
  5. 5.

    The photon may enter through the top of the detector and exit through side-2 of the detector, travelling distance, d 5, given by:

    $$ d_{5} = \left( {\frac{R}{\sin \theta }-\frac{h}{\cos \theta }} \right) $$
    (6)
  6. 6.

    The photon may enter through the top of the detector and exit through the base of the detector, travelling distance, d 6, given by:

    $$ d_{6} = \frac{L}{\cos \theta } $$
    (7)

The polar angle, θ, takes the values:

$$ \begin{aligned} \theta_{1} & = \, \tan^{-1} \left( {\frac{R}{h + L}} \right),\quad \quad \theta_{1}^{\prime} = \, \tan^{{-1}} \left({\frac{{R_{1} }}{{h + L_{1} }}} \right) \\ \theta_{2} & = \,\tan^{{-1}} \left( \frac{R}{h} \right) ,\quad \quad \theta_{2}^{\prime} = \, \tan^{{-1}} \left( {\frac{{R_{1} }}{h}} \right) \\ \end{aligned} $$
(8)

In addition, there are three sub-cases given by:

  1. 1.

    For \( \left( {\theta_{1}^{{\prime }} \le \theta_{1} < \theta_{2}^{{\prime }} } \right) \), the effective solid angle, Ω Eff (Point-Out), with possible different pass lengths as shown in Fig. 1(a) is given by:

    $$ \varOmega_{{{\text{Eff }}\,({\text{Point - Out}})}} \; = \;\sum\nolimits_{i \, = 1}^{n \, = \, 4} {\varOmega_{i} } $$
    (9)

    where

    $$ \begin{aligned} \varOmega_{1} & = \int\limits_{0}^{{\theta_{1}^{\prime} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{1} \;\sin \theta {\text{d}}\varphi \;{\text{d}}\theta } } ,\quad \varOmega_{2} = \int\limits_{{\theta_{1}^{\prime} }}^{{\theta_{1} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{2} \sin \theta {\text{d}}\varphi \;{\text{d}}\theta } } \\ \varOmega_{3} & = \int\limits_{{\theta_{1} }}^{{\theta_{2}^{\prime} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{4} \;\sin \theta {\text{d}}\varphi \;{\text{d}}\theta } } ,\quad \varOmega_{4} = \int\limits_{{\theta_{2}^{\prime} }}^{{\theta_{2} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{5} \sin \theta {\text{d}}\varphi \;{\text{d}}\theta } } \\ \end{aligned} $$
    (10)
  2. 2.

    For \( \left( {\theta_{1}^{{\prime }} \le \theta_{1} < \theta_{2}^{{\prime }} } \right) \), the effective solid angle, Ω Eff (Point-Out), with possible different pass lengths as shown in Fig. 1(b) is given by:

    $$ \varOmega_{\text{Eff}\,\text{(Point - Out)}} = \sum\nolimits_{i \, = 1}^{n \, = \, 4} {\varOmega_{i} } $$
    (11)

    where

    $$ \begin{aligned} \varOmega_{1} & = \int\limits_{0}^{{\theta_{1} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{1} \sin \theta {\text{d}}\varphi \,{\text{d}}\theta } } ,\quad \varOmega_{2} = \int\limits_{{\theta_{1} }}^{{\theta_{1}^{\prime} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{3} \sin \theta {\text{d}}\varphi\, {\text{d}}\theta } } \\ \varOmega_{3} & = \int\limits_{{\theta_{1}^{\prime} }}^{{\theta_{2}^{\prime} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{4} \sin \theta {\text{d}}\varphi\, {\text{d}}\theta } } ,\quad \varOmega_{4} = \int\limits_{{\theta_{2}^{\prime} }}^{{\theta_{2} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{5} \sin \theta {\text{d}}\varphi\,{\text{d}}\theta } } \\ \end{aligned} $$
    (12)
  3. 3.

    For \( \left( {\theta_{1}^{{\prime }} \le \theta_{2} < \theta_{1}^{{\prime }} } \right) \), the effective solid angle, Ω Eff (Point-Out), with possible different pass lengths as shown in Fig. 1(c) is given by:

    $$ \varOmega_{\text{Eff }\,\text{ (Point - Out)}} = \sum\nolimits_{i \, = 1}^{n \, = \, 4} {\varOmega_{i} } $$
    (13)

    where

    $$ \begin{aligned} \varOmega_{1} & = \int\limits_{0}^{{\theta_{1}^{\prime} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{1} \sin \theta {\text{d}}\varphi \,{\text{d}}\theta } } ,\quad \varOmega_{2} = \int\limits_{{\theta_{1}^{\prime} }}^{{\theta_{2}^{\prime} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{2} \sin \theta {\text{d}}\varphi\,{\text{d}}\theta } } \\ \varOmega_{3} & = \int\limits_{{\theta_{2}^{\prime} }}^{{\theta_{1} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{6} \sin \theta {\text{d}}\varphi\,{\text{d}}\theta ,} } \quad \varOmega_{4} = \int\limits_{{\theta_{1} }}^{{\theta_{2} }} {\int\limits_{0}^{2\pi } {f_{\text{att}} . \, f_{5} \sin \theta {\text{d}}\varphi\, {\text{d}}\theta } } \\ \end{aligned} $$
    (14)

    where \( f_{i} = \, (1-e^{{-\mu \cdot d_{i} }} ) \) and d i are the possible path lengths travelled by the photon within the detector active volume, d 1, d 2,…,d n, as discussed before, and the attenuation factor, f att, for the absorber layers with attenuation coefficients, μ 1, μ 2,…,μ n, and relevant thicknesses, t 1, t 2,…,t n, between the source and detector system is given by:

    $$ f_{\text{att}} = e^{{ - \sum\nolimits_{i \, = 1}^{n} {\mu_{i} \delta_{i} } }} \, $$
    (15)

    where the photon path lengths inside the absorber, δ i , are given by:

    $$ \begin{aligned} \delta_{i} & = \left( {\frac{{t_{i} }}{\cos \theta }} \right){\text{ For the front absorber layers}} \\ \delta_{i} & = \left( {\frac{{t_{i} }}{\sin \theta }} \right){\text{ For the side absorber layers}} \\ \end{aligned} $$
    (16)

In the case of an isotropic radiating axial point source located inside the detector’s well, the effective solid angle, Ω Eff (Point-In), can be calculated by dividing the well-type detector into two parts (upper and lower parts) with, outer radius, R, inner radius, R 1, base height (L + L 2), and depth (L 1 + L 2). Therefore, there are two cases to be considered for the photon emitted from a point source, P, at a definite position inside the detector cavity as shown in Fig. 2. Thus, the effective solid angle, Ω Eff (Point-In), is given by:

$$ \varOmega_{{\rm Eff}\,\text{(Point}- \text{In)}} = \varOmega_{{_{\text{Eff}\,\text{(upper}\,\text{part)}} }} + \varOmega_{{_{\text{Eff}\,\text{(lower}\,\text{part)}} }} {\text{ where: }} \varOmega = \int\limits_{\theta } {\int\limits_{\varphi } {f_{\text{att}} \cdot (1-e^{{-\mu \cdot d_{i} }} )\sin \theta {\text{d}}\varphi\, {\text{d}}\theta \, } } $$
(17)

where θ and φ are the polar and azimuthal angles, µ is the attenuation coefficient of the detector active medium for a γ-ray photon with energy, E γ , and d i are the possible photon path lengths inside the detector active volume. The factor, f att, is as identified before in Eq. (15).

Fig. 2
figure 2

Geometry of the source–detector system for non-axial point and cylindrical sources

Full size image

The quantities (ρ, L 1) identify the position of an arbitrarily positioned point source, P, the polar, θ, and the azimuthal, φ, angles at the point of entrance of the considered surface define the direction of the incidence of the photon. The effective photons travelling through the detector active volume traverse a distance, d, until it comes out from the detector. There are six allowed probabilities for the photons to enter and exit from the well-type detector upper and lower parts, respectively (covering distances, d 1, d 2, d 3, d 4 , d 5 and d 6) [14]. The effective solid angle, Ω Eff (upper part), of the upper part of the detector can be given by:

$$ \varOmega_{\text{Eff}\,\text{(upper}\,\text{part)}} = \sum\limits_{i \, = \, 1}^{i \, = \, 4} {\varOmega_{i} } \, $$
(18)

where

$$ \begin{aligned} \varOmega_{1} & = \int\limits_{{\frac{\pi }{2}}}^{{\theta_{4} }} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{4} {\text{d}}\varphi\, {\text{d}}\theta } } ,\quad \varOmega_{2} = \int\limits_{{\theta_{3}^{\prime} }}^{{\theta_{4}^{\prime} }} {\int\limits_{0}^{{\varphi_{UP}^{\prime} }} { \, f_{\text{att}} \cdot f_{5} {\text{d}}\varphi \,{\text{d}}\theta } } ,\quad \varOmega_{3} = \int\limits_{{\theta_{4} }}^{{\theta_{4}^{\prime} }} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{5} {\text{d}}\varphi\, {\text{d}}\theta } } \\ \varOmega_{4} & = \int\limits_{{\theta_{3} }}^{{\theta_{4} }} {\left[ {\int\limits_{0}^{{\varphi_{UP} }} { \, f_{\text{att}} \cdot f_{5} {\text{d}}\varphi \,{\text{d}}\theta - \int\limits_{0}^{{\varphi_{UP} }} { \, f_{\text{att}} \cdot f_{4} {\text{d}}\varphi \,{\text{d}}\theta } } } \right]} \\ \end{aligned} $$
(19)

with,

$$ f_{i} = (1-e^{{-\mu \cdot d_{i} }} )\sin \theta ,\quad i = {\text{4 and 5}} $$

For the lower part of the detector, there are two cases to be considered according to the relation between the extreme values of the photon angles, θ i . In the first case (\( \theta_{2}^{{\prime }} \le \, \theta_{2} < \pi /2 \)), there are two sub-cases based on the relation between \( \theta_{1}^{{\prime }} \), θ 1 and \( \theta_{2}^{{\prime }} \) as \( \left( {\theta_{1}^{{\prime }} \le \theta_{1} < \theta_{2}^{{\prime }} } \right) \) or \( \left( {\theta_{1}^{{\prime }} \le \theta_{2} < \theta_{1}^{{\prime }} } \right) \). In this case, the effective solid angle, Ω Eff (lower part), of the lower part is given by:

$$ \varOmega_{{{\text{Eff}}\,({\text{lower}\,\text{part}})}} = \sum\limits_{i \, = \, 1}^{i \, = \, 5} {\varOmega_{i} } $$
(20)

where

$$ \begin{aligned} \varOmega_{1} & = \int\limits_{0}^{{\theta_{1}^{\prime} }} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{1} {\text{d}}\varphi\,{\text{d}}\theta } } , \, \varOmega_{2} = \int\limits_{{\theta_{1}^{\prime} }}^{{\theta_{1} }} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{2} {\text{d}}\varphi\,{\text{d}}\theta } } , \, \varOmega_{3} = \int\limits_{{\theta_{1} }}^{{\frac{\pi }{2}}} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{4} {\text{d}}\varphi\,{\text{d}}\theta } } \\ \varOmega_{4} & = \int\limits_{{\theta_{1}^{\prime} }}^{{\theta_{2}^{\prime} }} {\left[ {\int\limits_{0}^{{\varphi_{\text{LO}}^{\prime} }} { \, f_{\text{att}} \cdot f_{{_{1} }} {\text{d}}\varphi\,{\text{d}}\theta - \int\limits_{0}^{{\varphi_{\text{LO}}^{\prime} }} { \, f_{\text{att}} \cdot f_{2} {\text{d}}\varphi\,{\text{d}}\theta } } } \right]} \\ \varOmega_{5} & = \int\limits_{{\theta_{1} }}^{{\theta_{2} }} {\left[ {\int\limits_{0}^{{\varphi_{\text{LO}} }} { \, f_{\text{att}} \cdot f_{2} {\text{d}}\varphi\,{\text{d}}\theta-\int\limits_{0}^{{\varphi_{\text{LO}} }} { \, f_{\text{att}} \cdot f_{4} {\text{d}}\varphi\,{\text{d}}\theta } } } \right]} \\ \end{aligned} $$
(21)

where

$$ f_{i} = \, (1-e^{{-\mu .d_{i} }} )\sin \theta ,\quad i = {\text{1, 2 and 4 }} $$

In the second case (\( \theta_{2} \le \theta_{2}^{{\prime }} < \pi /2 \)), there are also two sub-cases based on the relation between \( \theta_{1}^{{\prime }} \), θ 1 and the transfer angle, θ T , as (\( \theta_{1} \le \theta_{1}^{{\prime }} < \theta_{T} \)) or (\( \theta_{1}^{{\prime }} \le \theta_{1} < \theta_{T} \)). Therefore, the effective solid angle, Ω Eff (lower part), of the lower part of the detector in the two sub-cases can be given by following Eqs. (22)–(25), respectively.

$$ \varOmega_{\text{Eff}\,\text{(lower}\,\text{part)}} = \sum\limits_{i \, = \, 1}^{i \, = \, 5} {\varOmega_{i} } $$
(22)

where

$$ \begin{aligned} \varOmega_{1} & = \int\limits_{0}^{{\theta_{1} }} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{1} {\text{d}}\varphi \,{\text{d}}\theta } } ,\quad \varOmega_{2} = \int\limits_{{\theta_{1} }}^{{\theta_{1}^{\prime} }} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{3} {\text{d}}\varphi \,{\text{d}}\theta } } ,\quad \varOmega_{3} = \int\limits_{{\theta_{1}^{\prime} }}^{{\frac{\pi }{2}}} {\int\limits_{0}^{2\pi } { \, f_{\text{att}} \cdot f_{4} {\text{d}}\varphi \,{\text{d}}\theta } } \\ \varOmega_{4} & = \int\limits_{{\theta_{1}^{\prime} }}^{{\theta_{2}^{\prime} }} {\left[ {\int\limits_{0}^{{\varphi_{\text{LO}}^{\prime} }} { \, f_{\text{att}} \cdot f_{3} {\text{d}}\varphi\, {\text{d}}\theta -\int\limits_{0}^{{\varphi_{\text{LO}}^{\prime} }} { \, f_{\text{att}} \cdot f_{4} {\text{d}}\varphi \,{\text{d}}\theta } } } \right]} \\ \varOmega_{5} & = \int\limits_{{\theta_{1} }}^{{\theta_{2} }} {\left[ {\int\limits_{0}^{{\varphi_{\text{LO}} }} { \, f_{\text{att}} \cdot f_{1} {\text{d}}\varphi \,{\text{d}}\theta -\int\limits_{0}^{{\varphi_{\text{LO}} }} { \, f_{\text{att}} \cdot f_{3} {\text{d}}\varphi\, {\text{d}}\theta } } } \right]} \\ \end{aligned} $$
(23)

where

$$ f_{i} = (1-e^{{-\mu \cdot d_{i} }} )\sin \theta , \, i = {\text{ 1, 3 and 4}} $$

or else

$$ \varOmega_{\text{Eff}\,\text{(lower}\,\text{part)}} = \sum\limits_{i \, = \, 1}^{i \, = \, 6} {\varOmega_{i} } \, $$
(24)

with,

$$ \begin{aligned} \varOmega_{3} &= \int\limits_{{\theta_{1}^{\prime} }}^{{\theta_{1} }} \left[{\int\limits_{0}^{{\varphi_{\text{LO}}^{\prime} }} {f_{\text{att}} \cdot f_{1}{\text{d}}\varphi \,{\text{d}}\theta + \int\limits_{{\varphi_{\text{LO}}^{\prime} }}^{2\pi } {f_{\text{att}} \cdot f_{2} {\text{d}}\varphi\, {\text{d}}\theta } } } \right] \hfill \\ \varOmega_{4} &= \int\limits_{{\theta_{2} }}^{{\theta_{2}^{\prime} }} \left[{\int\limits_{0}^{{\varphi_{\text{LO}}^{\prime} }} {f_{\text{att}} \cdot f_{3} {\text{d}}\varphi \,{\text{d}}\theta + \int\limits_{{\varphi_{\text{LO}}^{\prime} }}^{2\pi } {f_{\text{att}} \cdot f_{4} {\text{d}}\varphi\, {\text{d}}\theta } } } \right] \hfill \\ \varOmega_{5} &= \int\limits_{{\theta_{1} }}^{{\theta_{T} }} \left[{\int\limits_{0}^{{\varphi_{\text{LO}}^{\prime} }} {f_{\text{att}} \cdot f_{1} {\text{d}}\varphi \,{\text{d}}\theta + \int\limits_{{\varphi_{\text{LO}}^{\prime} }}^{{\varphi_{\text{LO}} }} { \, f_{\text{att}} \cdot f_{2} {\text{d}}\varphi \,{\text{d}}\theta + \int\limits_{{\varphi_{\text{LO}} }}^{2\pi } {f_{\text{att}} \cdot f_{4} {\text{d}}\varphi \,{\text{d}}\theta } } } } \right] \hfill \\ \varOmega_{6} &= \int\limits_{{\theta_{T} }}^{{\theta_{2} }} \left[ {\int\limits_{0}^{{\varphi_{\text{LO}} }} {f_{\text{att}} \cdot f_{1} {\text{d}}\varphi \,{\text{d}}\theta + \int\limits_{{\varphi_{\text{LO}} }}^{{\varphi_{\text{LO}}^{\prime} }} { \, f_{\text{att}} \cdot f_{3} {\text{d}}\varphi \,{\text{d}}\theta + \int\limits_{{\varphi_{\text{LO}}^{\prime} }}^{2\pi } {f_{\text{att}} \cdot f_{4} {\text{d}}\varphi\, {\text{d}}\theta } } } } \right] \hfill \\ \end{aligned} $$
(25)

where

$$ f_{i} = \, (1-e^{{-\mu .d_{i} }} ) \, \sin \theta ,\quad i = {\text{1, 2, 3 and 4}} $$

Setting of ρ = 0 leads to an arbitrarily positioned isotropic radiating axial point source case, where the numerical evaluation of the double integrals is performed using the trapezoidal rule. A computer program has been developed to evaluate the effective solid angle of the well-type detector with respect to the previous source at any source–detector partition. The accuracy of the integration increases by increasing the number of the intervals under the integration, n; it has been stated that the integration converges very well at n = 30.

In the case of an isotropically irradiating volume source, not all emitted from its radioactive nuclei photons exit the source volume with the same energy, a part of them is absorbed in the source itself [15]. This self-absorption factor S f is defined by:

$$ S_{\text{f}} = \, e^{{ - \mu_{s} \cdot \, d_{s} }} , $$
(26)

where µ s is the source medium attenuation coefficient, d s , the distance travelled by the photon within the source substance, is a function of the polar θ and azimuthal φ angles, where angles (θ 5–θ 8) are the extreme polar angles of the source [14].

The radioactive cylindrical source can be considered as a volume source as shown in Fig. 2 consisting of a group of point sources, P, uniformly distributed, each having an effective solid angle, Ω Eff (Point-In), and then, the effective solid angle, Ω Eff (Cyl-In), of the well-type detector in case of using a volume source inside is given by:

$$ \varOmega_{{{\text{Eff}\,\text{ (Cyl - In}})}} = \, \frac{{\int\limits_{V} {S_{\text{f}} . \, \varOmega_{\text{Eff}\,\text{ (Point - In)}} {\text{d}}V} }}{V} \, $$
(27)

where V is the volume of the radioactive source. For any element of volume,\( {\text{d}}V \, = \, \rho {d}\rho\,{d}\alpha\,{d}h \) displaced a lateral distance, ρ, from the detector axis, with angular coordinate, α; then, the Eq. (27) can be rewritten as:

$$ \varOmega_{\text{Eff}\,\text{ (Cyl - In)}} = \frac{{\int\limits_{h} {\int\limits_{\alpha } {\int\limits_{\rho } {S_{\text{f}} . \, \varOmega_{\text{Eff}\,\text{(Point}-\text{In)}} \, \rho d\rho\,d\alpha\,{d}h} } } }}{{\pi S^{2} L_{3} }} $$
(28)

Thus, the effective solid angle, Ω Eff (Cyl-In) of the well-type detector in case of using a cylindrical source of radius, S, and height, L 3, can be expressed by:

$$ \varOmega_{\text{Eff}\,\text{(Cyl - In)}} = \frac{{\int\limits_{{h_{o} }}^{{h_{o} + \, L_{3} }} {\left( {\int\limits_{0}^{2\pi } {\int\limits_{0}^{S} {S_{\text{f}} \cdot \varOmega_{\text{Eff}\,\text{(upper}\,\text{part)}} \rho d\rho d\alpha + \int\limits_{0}^{2\pi } {\int\limits_{0}^{S} {S_{\text{f}} \cdot \varOmega_{\text{Eff}\,\text{(lower}\,\text{part)}} \, \rho d\rho d\alpha } } } } } \right){\text{d}}h} }}{{\pi S^{2} L_{3} }} \, $$
(29)

The full-energy peak efficiency of the well-type detector, using cylindrical radioactive sources, can be calculated based on the reference measured full-energy peak efficiency using a point source, located outside the well-type detector cavity by the following formula:

$$ \varepsilon_{{ ( {\text{Cyl - In)}}}} = \frac{{\varOmega {}_{\text{Eff}\,\text{(Cyl - In)}}}}{{\varOmega_{{_{\text{Eff}\,\text{ (Point - Out)}} }} }}\varepsilon_{{ ( {\text{Point - Out)}}}} $$
(30)

where \( \varepsilon_{{ ( {\text{Cyl - In)}}}} \) and \( \varepsilon_{{ ({\text{Point - Out)}}}} \) are the full-energy peak efficiency for using a cylindrical radioactive source and point source, located outside the well-type detector as a reference geometry, respectively, \( \varOmega {}_{\text{Eff}\,\text{ (Cyl - In)}} \) and \( \varOmega_{{_{\text{Eff}\,\text{(Point - Out)}} }} \) are the effective solid angles subtended by the detector surface with the cylindrical source and the reference geometry, respectively.

To establish the idea of the correction for the coincidence summing effects when using a volume source with homogeneously distributed activity [16], one can examine some simple cascade transitions as in 60Co and 88Y. It is required to know the spatial dependence of the detector efficiencies within the detector volume. The correction factors for the gamma lines γ 21, γ 10 and γ 20, corresponding to the transitions between the energy states (1 and 0, 2 and 1), are given by:

$$ \begin{aligned} C_{10} &= \left( {1-P_{21} \cdot \, \varepsilon_{{ ( {\text{Cyl - In)}}21T}} } \right)^{ - 1} \hfill \\ C_{21} &= \left( {1-P_{10} \cdot \varepsilon_{{ ( {\text{Cyl - In)}}10T}} } \right)^{ - 1} \hfill \\ C_{20} &= \left( {1 + \frac{{P_{10} P_{21} }}{{P_{20} }} \cdot \frac{{\varepsilon_{{ ( {\text{Cyl - In)}}10P}} \cdot \varepsilon_{{ ( {\text{Cyl - In)}}21P}} }}{{\varepsilon_{{ ( {\text{Cyl - In)}}20P}} }}} \right)^{ - 1} \hfill \\ \end{aligned} $$
(31)

where P 10, P 21 and P 20 are the emission probabilities of γ-lines γ 10, γ 21 and γ 20, while \( \varepsilon_{{({\text{Cyl - In}})10P}} \), \( \varepsilon_{{({\text{Cyl - In}})21P}} \) and \( \varepsilon_{{({\text{Cyl - In}})20P}} \) are the full-energy peak efficiencies with respect to the these lines. Besides \( \varepsilon_{{({\text{Cyl - In}})10T}} \) and \( \varepsilon_{{ ( {\text{Cyl - In)}}21T}} \) are the total efficiencies which reduce the counts under the peaks γ 10 and γ 20 and can be calculated based on Ref. [15]. In Eq. (31), it is assumed that for a volume source of 1 ml the effective total efficiencies [17] are practically equal to the usual total efficiencies.

In the well-type detector geometry, the coincidence summing effects are high and make the determination of the full-energy peak efficiency difficult with standard calibration point sources. The efficiency calibration procedure that is performed with usual mixed gamma-ray standard source cannot provide a correct efficiency calibration curve, because there are important coincidence losses involved when counting the lines of 60Co and 88Y, which leads to a biased calibration curve in the high-energy range. Besides, there is no practical nuclide emitting only one gamma-quantum that would extend the calibration curve up to ~2000 keV.

3 Experimental setup

The full-energy peak efficiency values were measured in laboratory for γ-ray spectrometry of the Belgium Nuclear Research Center (SCK.CEN), MOL, Belgium, for the p-type HPGe well-type detector (Model GCW6023-Canberra) of 300 cm3 active volume, with relative efficiency at 1.33 MeV equal to 68.2 %. The manufacturer parameters are shown in Fig. 3, and the SCK.CEN electronics setup values for this detector are shown in Table 1. The activity standards in the form of point sources were used for the calibration of gamma-spectrometers. The radioactive substance was a very thin, circular deposit with about 5 mm in diameter, in the middle of two polyethylene foils, each having a mass per unit area of (21.3 ± 1.8) mg cm−2. By heating under pressure, the two foils were welded together over the whole area so that they were leaked-proofed. To facilitate handling, the foil 26 mm diameter in diameter was mounted in a circular aluminium ring (outer diameter: 30 mm, height: 3 mm) from which it could easily be removed if and when required. These point sources (241Am, 137Cs, 133Ba and 152Eu) were purchased from the Physikalisch-Technische Bundesanstalt (PTB) in Braunschweig and Berlin, which is the German metrology institute and the highest technical authority of the Federal Republic of Germany in the field of metrology and certain sectors of safety engineering. The sources were measured at 26 cm from the surface of the cavity of well-type detector, where 0.1-cm-thick Plexiglas cover was used.

Fig. 3
figure 3

Industrial drawing of the detector provided by the Canberra company

Full size image
Table 1 Setup values of the well-type HPGe detector and the source at SCK.CEN
Full size table

The radioactive source container was high-density polyethylene (HDPE) plastic standard vials supplied by the Department for Fine Mechanics of the Biological Laboratory of the Free University of Amsterdam and containing an aqueous solution of volume 0.7 ml. The several radionuclides (241Am, 109Cd, 57Co, 123mTe, 113Sn, 85Sr, 137Cs, 51Cr, 88Y and 60Co) were mixed in the water matrix from Eckert and Ziegler Isotope Products Laboratories (IPL) USA—Source No. 1160-56, reference date: 2006-05-01(21H00). The source dimensions plus source activities and uncertainties are given in Table 1. All the volume sources were measured and placed directly inside the well-type detector cavity on the entrance window, so the source-to-detector separations were taken to be very small in order to neglect the angular correlation effects.

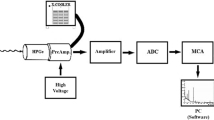
The practical measurements were taken using a multichannel analyser (MCA) to obtain statistically significant main peaks in the amplitude spectra, which were recorded and processed by ISO 9001 Genie 2000 data acquisition and analysis software made by Canberra [18]. The acquisition time was as long as necessary to get at least 20,000 counts under the full-energy peak, which gave a statistical uncertainty of less than 1 %. The peak fitting was performed using a Gaussian function without a low-energy tail (for HPGe detectors) [19]. The activity of the each radionuclide source was kept low to avoid high counting rates when measuring at a small distance [15], in order to minimize dead time and pile-up effects.

The peak areas, live time, real time and starting time for each spectrum were entered in the spreadsheet used to calculate the efficiency curves. Then, the efficiency transfer method (ET) was used to calculate the coincidence summing factors, to correct the measured full-energy peak efficiencies and to obtain the true efficiency.

4 Results and discussion

The true full-energy peak efficiency values, as a function of the gamma-ray energy [8], for the HPGe well-type detector (p-type) with radioactive point sources and plastic vial source of volumes 1 ml, are determined by the following equation:

$$ \varepsilon \left( E \right) = \frac{N(E)}{{T \cdot A_{S} \cdot P(E)}}\mathop \prod \nolimits C_{i} $$
(32)

where: N (E) is the number of counts in the full-energy peak, as calculated by Genie 2000 software, T is the live time (in seconds), P(E) is the intensity of gamma-ray with energy E, A S is the radionuclide activity, C i are the correction factors taking into account the radionuclide decay and coincidence summing. The decay correction C d for the calibration source from the reference time to the acquisition time is given by equation:

$$ C_{d} = e^{\lambda \cdot \Delta T} $$
(33)

where λ is the decay constant, ΔT is the time interval over which the source decays. The main source of uncertainty in the efficiency calculations is the uncertainties in the activities of the standard source solutions. Coincidence summing effects are negligible in the reference measurement geometries due to the large source–detector distance. Once the efficiencies have been fixed by applying the correction factors, the overall efficiency curve is obtained by fitting a polynomial logarithmic function of fifth order to the experimental points using a nonlinear least square fit, based on the following equations:

$$ \log (\varepsilon ) \, = \sum\limits_{i = o}^{5} {a_{i} } .\log (E)^{i} \, , \, \sigma_{{_{\log (\varepsilon )} }}^{2} = \left( {\frac{1}{\varepsilon }} \right)^{2} . \, \sigma_{\varepsilon }^{2} {\text{ and }}W_{i} = \left( {\frac{\varepsilon }{{\sigma_{\varepsilon } }}} \right)^{2} $$
(34)

where a i are the coefficients to be determined by the calculations, ε is the full-energy peak efficiency at energy E, σ log(ε) is the variance of log(ε), W i is the weighting factor of ith experimental data point. In this way, the correlation between data points of the same calibration source has been included to avoid the overestimation of the experimental efficiency uncertainties. The overall uncertainty for the full-energy peak efficiency σ ε is given by the equation:

$$ \sigma_{\varepsilon } = \varepsilon \cdot \sqrt {\left( {\frac{\partial \varepsilon }{\partial A}} \right)^{2} \cdot \sigma_{A}^{2} + \left( {\frac{\partial \varepsilon }{\partial P}} \right)^{2} \cdot \sigma_{P}^{2} + \left( {\frac{\partial \varepsilon }{\partial N}} \right)^{2} \cdot \sigma_{N}^{2} } $$
(35)

where σ A , σ P and σ N are the uncertainties associated with the quantities A S , P(E) and N(E), respectively, assuming that the only correction made is due to the source activity decay [20]. The coincidence correction factors for 60Co and 88Y have been calculated from Eq. (32) and used to determine the true full-energy peak efficiency. The relation between the log(ε) and log(E) with the associated uncertainties using point sources (241Am,137Cs,133Ba and 152Eu) measured at 26 cm from the surface of the cavity of well-type detector with the fitting curve using a polynomial of order 5 is shown in Fig. 4. The fourteen fitting full-energy peak efficiency values of using point source [Point-out] which it measured at 26 cm as a function of the gamma-ray energy based on the volume source energies have been extracted using the polynomial function from Fig. 4 and exemplified in Fig. 5. The measured full-energy peak efficiency values with the associated uncertainties for volume sources (1 ml) measured inside the cavity of the well-type detector and the fitting full-energy peak efficiency values for point source [Point-out] at 26 cm as a function of the photon energy are shown in Fig. 6. The calculated ET based on Eq. (31) and measured full-energy peak efficiency values with the associated uncertainties as a function of the photon energy in the energy range 60 up to 1836 keV for a cylindrical geometry are displayed in Fig. 7. The ratio of the effective solid angles subtended by the detector between the volume source measured inside the cavity and the point source at 26 cm as a function of the energy is represented in Fig. 8.

Fig. 4
figure 4

Relation between the Log(ε) and Log(E) with the associated uncertainties for using point sources (241Am,137Cs,133Ba and 152Eu) measured at 26 cm from the surface of the cavity of well-type detector beside the fitting curve using polynomial of order 5

Full size image
Fig. 5
figure 5

Fourteen fitting full-energy peak efficiency values for using point source (Point-out) at 26 cm as a function of the photon energy based on the volume source energy

Full size image
Fig. 6
figure 6

Measured full-energy peak efficiency values for using volume source (1 ml) measured inside the cavity of the well-type detector and the fitting full-energy peak efficiency values for using point source (Point-out) at 26 cm as a function of the photon energy

Full size image
Fig. 7
figure 7

True full-energy peak efficiency for calculated (ET) and measured values with the associated uncertainties as a function of the photon energy for (1 ml) geometry

Full size image
Fig. 8
figure 8

Ratio of the effective solid angle as a function of the photon energy between the solid angle of the volume source (1 ml) inside the cavity of the well-type detector and the solid angle of the point source (Point-out) at 26 cm subtended with the detector

Full size image

The relative differences between the calculated and the measured true full-energy peak efficiency values [6] are given by the following equation:

$$ \Delta \% \, = \frac{{\varepsilon_{\text{calculated}} -\varepsilon_{\text{measured}} }}{{\varepsilon_{\text{calculated}} }} \times 100 \, $$
(36)

By comparison, the percentage differences are being around 8 %, using the efficiency transfer method (ET) in integral form.

5 Conclusions

The efficiency transfer method (ET) in an integral form has been used successfully with relative differences being around 5 % to produce the full-energy peak efficiency curve for the p-type HPGe well-type detector calibrated with radioactive point sources measured out the well-type detector cavity and the volume cylindrical source fitted inside the well-type detector cavity. In addition, the source self-absorption factors and the coincidence correction factors for using volume sources have been calculated using the efficiency transfer method (ET) to correct the efficiency values.