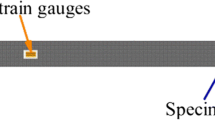1 Introduction

Strain gauges experience a change of an electrical parameter, usually their resistance, when they are stretched or strained being indestructibly located on special elastic elements [1, 2]. Strain gauges present a significant measurement challenge to measure mechanical movements in micro level. Accurate measurement of small change in resistance is critical in case of strain gauge [3].

Bridge circuits are a time-honored way to make accurate measurements of resistance and some other electrical parameters [4]. Wheatstone bridge offers a good method for measuring small resistance changes accurately and allows a differential measurement that offers a higher common-mode noise rejection than in a single-element measurement [5]. Therefore, it is used for sensing most of the resistive type sensors that include the measurement of temperature, strain, pressure, fluid flow, and relative humidity etc. Today, Wheatstone bridge is a basic structure for measurement in various measuring systems [6].

Several endeavours have been practiced and still going on to improve the quality of measurement using wheatstone bridge for its very high potential in the field of precision measurement. Yonce et al. developed a system for DC autonulling bridge for real time resistance measurement. The DC autonulling bridge builds upon the wheatstone bridge configuration to measure sensor resistance by maximizing noise rejection and dynamic range, and also allowing real time monitoring of transient resistance changes [5]. Sun et al. [7] developed a signal conditioning and a data acquisition system including hardware and software implementation which can effectively measure weak signal using wheatstone bridge. A modified wheatstone bridge for the high-value resistance measurement from 1 MΩ to 1 TΩ is developed by Oe et al. [8]. The uncertainties of high resistance bridges are explained in that study. Boujamaa et al. proposed a feedback conditioning architecture to improve the power supply noise rejection of a wheatstone bridge [9]. Putter [10] has presented a paper on on-chip RC measurement and calibration circuit using wheatstone bridge. A fully automated measurement system has been developed for calibrating 1 Ω resistance standards using a modified wheatstone bridge by Hitoshi et al. [11].

In general strain gauges are used in a bridge configuration with a voltage or current excitation source. A strain-gauge test facility was designed and constructed to study the output signals resulting from gauges operating normally under sinusoidally varying strain and in two common failure modes, namely, debonding and loose termination by Ellis and Smith [12]. The widely used strain gauge bridge circuit topologies are quarter bridge, half bridge and full bridge configurations [13]. Pal et al. has developed and implemented for calibrating strain amplifiers used in strain data acquisition systems. The traceability for the strain measurement in terms of voltage has been established [14]. The output voltage variation is proportional to the relative resistance variation of the wheatstone bridge. The sensitivity of the bridge depends on type of bridge configuration used. The stability of the excitation voltage or current directly affects the overall accuracy of the bridge output. The excitation source may be voltage (AC or DC) or current.

All the strain measuring circuits have some amount of uncertainty associated with them. Walendziuk [15] studied the measurement uncertainty analysis of the strain gauge based stabilographic platform. For uncertainty analysis there are two approaches.

  1. 1.

    The Type A evaluation of standard uncertainty is the method of evaluation by the statistical analysis of observations [16–19].

  2. 2.

    The Type B evaluation of standard uncertainty is the method of evaluation by other information about the measurement [17–20].

In this paper a strain gauge based measurement system is presented. Quarter bridge configuration is chosen for reducing the uncertainty as well as the cost. The paper presents the details of a signal conditioning circuit to get the final output voltage in the form of DC although the bridge is excited with an AC voltage. The associated uncertainty of the system is evaluated for both A and B type and presented in the paper.

2 Description of Signal Conditioning Circuit

The block diagram of the signal conditioning circuit is shown in Fig. 1. The resistive strain gauge (part no. CF350-2AA(11)C20) has a nominal resistance of 350 Ω with gauge factor 2.13 ± 1 %. A 1 kHz, 16.52 V (peak to peak) sinusoidal signal from the Agilent Generator (model no. 33220A) is used to excite the bridge. The differential output of the bridge is amplified by the instrumentation amplifier (AD620) and the amplified AC output is converted to DC by using peak detector. AC excitation is more advantageous as it removes offset errors, average out 1/f noise, and eliminates effects due to parasitic thermocouples. Also the effects of electromagnetic interferences due to line frequency (50 Hz) are minimized.

Fig. 1
figure 1

Block diagram of the signal conditioning circuit of the resistive sensor

Full size image

3 Implementation

3.1 Bridge Design

Three resistors of 350 Ω ± 0.1 % and temperature coefficient of ±5 ppm/°C are used in the bridge. The strain gauge is connected to the fourth arm of the bridge (Fig. 2).

Fig. 2
figure 2

Bridge circuit

Full size image

Use of 0.1 % tolerance and temperature coefficient of ±5 ppm/°C resistors ensures stability of bridge.

3.2 Sensitivity of the Bridge

The bridge output voltage, V 1 can be expressed as

$$ V_{1} = \frac{{V_{\text{in}} }}{4} \times \frac{{\Delta R}}{R} $$
(1)

where, V 1 is the output voltage, V in the excitation voltage, ∆R the change in resistance of the sensor and R is the resistance of the sensor in the unstrained condition.

Gauge factor (GF) of a strain gauge is given by, [21]

$$ {\text{GF}} = \frac{{{\raise0.7ex\hbox{${\Delta R}$} \!\mathord{\left/ {\vphantom {{\Delta R} R}}\right.\kern-0pt} \!\lower0.7ex\hbox{$R$}}}}{{{\raise0.7ex\hbox{${\Delta L}$} \!\mathord{\left/ {\vphantom {{\Delta L} L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} = 2.13 \pm 1\;\% $$
(2)

where, ∆L is the change in length of the specimen and L is original length of the specimen.

Using (1) and (2), the sensitivity is obtained as

$$ \begin{aligned} \frac{{V_{1} }}{{{\raise0.7ex\hbox{${\Delta L}$} \!\mathord{\left/ {\vphantom {{\Delta L} L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} & = \frac{{V_{\text{in}} }}{4} \times {\text{GF}} \\ & = 8.80\;{\text{V}}\quad [\Delta L/L = \varepsilon = {\text{strain}}] \\ \end{aligned} $$
$$ \frac{{V_{1} }}{\varepsilon } = 8.80 \times 10^{ - 6} \;{\text{V}}/\upmu {\text{strain}}$$
(3)

3.3 Instrumentation Amplifier

AD620 is used to provide a gain of 495 and for removing any common mode signal coming out of the bridge. It is a high accuracy instrumentation amplifier that requires only one external resistor to set the gain in the range of 1–1000. The AD620, with its high accuracy of 40 ppm maximum nonlinearity, low offset voltage of 50 µV maximum and offset drift of 0.6 µV/°C [22] (Fig. 3).

Fig. 3
figure 3

Instrumentation amplifier circuit

Full size image

The gain equation is

$$ G = \frac{49.4\;k\varOmega }{{R_{\text{g}} }} + 1 $$
(4)

where, R g is the gain setting resistor having value of 100 Ω. Therefore for our case, G = 495

3.4 Peak Detector

Peak detector circuit is shown in Fig. 4. The detected peak voltage charges the capacitor C3. The capacitor is discharged through R2 to store new value. Thus a DC voltage is obtained at the output. The DC output voltage V out is given by

$$ V_{\text{out}} = V_{2} /2 $$
(5)

where, V 2 is the peak to peak output of the instrumentation amplifier.

Fig. 4
figure 4

Peak detector circuit

Full size image

3.5 Transfer Function of the System

Transfer function is derived as follows:

Voltage output (V 2) of the amplifier is

$$ \begin{aligned} \, V_{2} & = {\text{Gain}} \times V_{1} \\ & = \left( {\frac{49.4\;k\varOmega }{{R_{\text{g}} }} + 1} \right) \times \frac{{V_{\text{in}} }}{4} \times \frac{{\Delta R}}{R} \\ \end{aligned} $$
(6)

where, V 1 is the bridge output voltage.

Using (3) and (4), we get

$$ \begin{aligned} \frac{{V_{2} }}{\varepsilon } & = {\text{Gain}} \times 8.8 \times 10^{ - 6} \;{\text{V}}/\upmu {\text{strain}} \\ \frac{{V_{2} }}{\varepsilon } & = \left( {\frac{49.4\;k\varOmega }{{R_{\text{g}} }} + 1} \right) \times 8.8 \times 10^{ - 6} \;{\text{V}}/\upmu {\text{strain}} \\ \end{aligned} $$
(7)

Since peak detector detects the peak of amplified output of the Instrumentation amplifier the transfer function becomes

$$ \frac{{V_{\text{out}} }}{\varepsilon } = \left( {\frac{49.4\,k\varOmega }{{R_{\text{g}} }} + 1} \right) \times 4.4 \times 10^{ - 6} \;V/\upmu {\text{strain}} $$
(8)

4 Calibration of the System

A rectangular beam of stainless steel is used to make a cantilever. The beam is fixed at one end and loaded at the other end using knife edge to remove shearing effect. The mass of the loads are measured by a balance (model no: AB54, make: Metler Toledo) prior to the experiment. Three strain gauges are attached to the surface of the beam with adhesive (cyanoacrylate) to measure tensile strain. Before attaching the strain gauges, the surface of the beam is cleaned and polished. The gauges are at X cm from the load. Strain gauge S1 is at the principal axis (geometrically measured at the half of the width) of the beam which is used for calibration and S2 and S3 are at 3 mm from the principal axis used to study the effect of shearing strain (Fig. 5).

Fig. 5
figure 5

System calibration setup

Full size image

The bridge output of each of the strain gauges are measured independently using Agilent DMM (Model no: 34401A) and recorded.

The tensile strain (ɛ) for a cantilever is given by [23, 24]

$$ \varepsilon = \frac{{6\;{m\text{g}}X}}{{bh^{2} E}} $$
(9)

where, m is the mass of the load, g is the acceleration due to gravity (9.78049 m/s2), X is the distance from the strain gauge to load (0.2 m), b is width of the cantilever beam (0.0184 m), h is thickness of the beam (0.00154 m), E is Young’s modulus of the stainless steel (180 × 109 N m−2).

The error in the measurement of tensile strain involves contribution from the measurements of the following factors m, X, b and h. The instrumental error in measuring m is ∂m = 1 × 10−7 kg,

$$ \partial X = \partial b = \partial h = 1 \times 10^{ - 3} \;{\text{m}}. $$

Hence, the total fractional error is calculated as

$$ \begin{aligned} \frac{\delta (\varepsilon )}{\varepsilon } & = \sqrt {\frac{{\delta_{m}^{2} }}{{m^{2} }} + \delta_{x}^{2} \left[ {\frac{1}{{X^{2} }} + \frac{1}{{b^{2} }} + \frac{1}{{h^{2} }}} \right]} \\ & = 944.44 \times 10^{ - 3} \\ \end{aligned} $$

The calculated strain and output voltages for different loads are shown in Table 1. Using Table 1 the output voltages for corresponding strain are plotted (shown in Fig. 6).

Table 1 Calculated strain and output voltages for different loads
Full size table
Fig. 6
figure 6

Calibration curve

Full size image

The data are fitted with a calibration curve as shown in Fig. 6.

The calibration curve is given as

$$ y = 2.281x + 1286 $$
(10)

where, y represents the output voltage and x is the microstrain.

The slope of the fitted curve gives a measure of the sensitivity of the system in mV per microstrain. From this analysis, the error in output voltage is found to be 1.76 mV.

The deviation of the measured voltage from the expected value is shown in Fig. 7.

Fig. 7
figure 7

Residual versus independent plot

Full size image

5 Effect of Sensor Misalignment

Misalignment of sensor may produce error in calibration. Due to sensor misalignment shearing strain may occur. To study the effect of shearing strain, the output voltages for the three sensors (shown in Fig. 5) are recorded and their corresponding sensitivities are observed using least square regression method. Table 2 shows the observations.

Table 2 Sensitivity of the Sensors
Full size table

From the observation, it is found that the average change of sensitivity is 0.02 mV/µstrain/mm due to misalignment of sensor from the principal axis. Therefore, the percentage change of sensitivity due to misalignment is 0.88 %/µstrain/mm.

6 Uncertainty Evaluation of the System

6.1 Relative Uncertainty of the System

The uncertainty of the measurement system depends on various factors, e.g. the supply voltage of the bridge, tolerance of the fixed resistors and strain gauge. In order to calculate the value of measurement uncertainty the bridge output voltage (V 1) is fed to the instrumentation amplifier and the amplifier output voltage V 2 is applied to the peak detector circuit.

Now the DC output voltage is given by

$$ V_{\text{out}} = \left( {\frac{{ 4 9. 4\;{\text{k}}\varOmega }}{{R_{\text{g}} }} + 1} \right) \times \frac{{V_{\text{in}} }}{8} \times \frac{\Delta R}{R} $$
(11)

Excluding the constant terms (since they don’t contribute uncertainty) relative uncertainty of the output, V 2, is calculated as below.

$$ \, \frac{{u(V_{2} )}}{{V_{2} }}{ = }\sqrt {\left[ {\frac{{u(R_{\text{g}} )}}{{R_{\text{g}} }}} \right]^{2} + \left[ {\frac{{u(V_{\text{in}} )}}{{V_{\text{in}} }}} \right]^{2} + \left[ {\frac{{u(R_{\text{sg}} )}}{{R_{\text{sg}} }}} \right]^{2} + \left[ {\frac{u(R)}{R}} \right]^{2} } $$

where, R g is gain setting resistor with tolerance 1 %, V in is excitation voltage, R sg is strain gauge’s resistance with tolerance 1 %, R is fixed resistor with tolerance 0.1 %.

$$ \begin{aligned} \frac{{u(V_{2} )}}{{V_{2} }} & = \sqrt {\left[ {\frac{1}{100}} \right]^{2} + \left[ {\frac{1}{8259}} \right]^{2} + \left[ {\frac{3.5}{350}} \right]^{2} + \left[ {\frac{.35}{350}} \right]^{2} } \\ \frac{{u(V_{2} )}}{{V_{2} }} & = 1 . 4 1 8\times 1 0^{ - 2} \\ \end{aligned} $$

In the above calculation temperature coefficient of resistors (±5 ppm/°C) is ignored due to very small (1.43 × 10−6 %) contribution to uncertainty.

6.2 Type B Uncertainty Analysis

Type B uncertainties are tabulated in Table 3.

Table 3 Standard type B uncertainty
Full size table

6.3 Type A Uncertainty Analysis

The Type A uncertainty analysis is done by the statistical data obtained from observations. The dominant sources of uncertainties are

  1. i)

    Bridge and

  2. ii)

    Signal Conditioning Circuit.

The estimated standard uncertainty (u) can be calculated as [16, 25, 26]

$$ u = \frac{\sigma }{\sqrt n } $$
(12)

where, \( \sigma \) is standard deviation (SD), n is the number of measurements in a set.

The combined uncertainty (u c) for two individual uncertainties u 1 and u 2 is calculated as [16]

$$ u_{c} = \sqrt {\left[ {u_{1} } \right]^{2} + \left[ {u_{2} } \right]^{2}} $$
(13)

6.4 Uncertainty in Bridge

The bridge comprises of three resistors of nominal value 350 Ω with 0.1 % tolerance and temperature coefficient of ±5 ppm/°C and one strain gauge is connected to the fourth arm of the bridge. For unstrained condition, a dummy strain gauge is fixed in a FR4 PCB (insulating side) with adhesive (cyanoacrylate). The bridge is excited by a 1 kHz, 16.52 V (peak to peak) source.

To get the bridge output voltage, V 1 at unstrained condition (Fig. 2), 45 data are recorded by Agilent DMM (model no. 34401A). Figure 8 shows the variation of recorded ac voltage (Table 4).

Fig. 8
figure 8

Bridge output

Full size image
Table 4 Type A uncertainty of the bridge
Full size table

6.5 Uncertainty in Signal Conditioning

To get the measurement uncertainty of the signal conditioning circuit, a 20 mV (peak to peak) signal from same function generator is applied to the input of the instrumentation amplifier. The recorded output voltage V out of the system is shown in Fig. 9.

Fig. 9
figure 9

Output voltage of the signal conditioning circuit

Full size image

The average V out is 5 V and the standard deviation of the signal conditioning circuit is 0.0164 V (Table 5).

Table 5 Type A uncertainty of the signal conditioning circuit
Full size table

6.6 Total Measurement Uncertainty of the System

Type A uncertainty in terms of µstrain is

  • The combined uncertainty (u c) is

    $$ \begin{aligned} &= \sqrt {\left[ {1.63 \times 10^{ - 5} } \right]^{2} + \left[ {1.29 \times 10^{ - 3} } \right]^{2} } \hfill \\ &= 1.3 \times 10^{ - 3} \, \upmu \text{strain} \hfill \\ \end{aligned} $$

From the calibration Eq. (9), the sensitivity obtained is 2.281 mV/µstrain.

Therefore, type A uncertainty in µstrain is estimated as

$$ \frac{{u_{c} }}{2.281} = \frac{1.3}{2.281} = \pm 0.570\;\upmu \text{strain} $$

7 Uncertainty Comparison Between Full Bridge and Quarter Bridge

For full bridge, the relative uncertainty of the equivalent resistance of the bridge is calculated as

$$ \begin{aligned} &= \sqrt {\left[ {\frac{{u(R_{sg} )}}{{R_{sg} }}} \right]^{2} + \left[ {\frac{{u(R_{sg} )}}{{R_{sg} }}} \right]^{2} + \left[ {\frac{{u(R_{sg} )}}{{R_{sg} }}} \right]^{2} + \left[ {\frac{{u(R_{sg} )}}{{R_{sg}^{{}} }}} \right]^{2} } \hfill \\ & = \sqrt {\left[ {\frac{3.5}{350}} \right]^{2} + \left[ {\frac{3.5}{350}} \right]^{2} + \left[ {\frac{3.5}{350}} \right]^{2} + \left[ {\frac{3.5}{350}} \right]^{2} } \hfill \\ &= 0.02 \hfill \\ \end{aligned} $$

The relative uncertainty of the equivalent resistance of the quarter bridge is calculated as

$$ \begin{aligned} &= \sqrt {\left[ {\frac{u(R)}{R}} \right]^{2} + \left[ {\frac{u(R)}{R}} \right]^{2} + \left[ {\frac{u(R)}{{R_{{}} }}} \right]^{2} + \left[ {\frac{{u(R_{sg} )}}{{R_{sg} }}} \right]^{2} } \hfill \\ &= \sqrt {\left[ {\frac{0.35}{350}} \right]^{2} + \left[ {\frac{0.35}{350}} \right]^{2} + \left[ {\frac{0.35}{{350_{{}} }}} \right]^{2} + \left[ {\frac{3.5}{350}} \right]^{2} } \hfill \\ &= 0.01 \hfill \\ \end{aligned} $$

The relative uncertainty of the equivalent resistance is reduced to half in quarter bridge.

8 Conclusion

A strain measurement system is designed, developed and calibrated. The uncertainty associated with the system is evaluated. The sensitivity of the developed system obtained from the transfer function, (8), is 2.2 mV/µstrain. The calibration equation, (10) gives the sensitivity of 2.1 mV/µstrain i.e. the theoretical and the experimental results show a good agreement. The developed measurement system is capable of measuring strain in the range of microstrain with an uncertainty of ±0.57 µstrain.

The calibration is done using a reliable and convenient method which can be easily set up in a laboratory environment.

The bridge can be excited by DC, but AC excitation is more advantageous compared to DC such as keeping the excitation frequency greater than 50 Hz/60 Hz, the electromagnetic interference due to line frequency can easily be removed.

Since only one strain gauge is used in quarter bridge configuration, by using precision resistors (tolerance 0.1 %, temperature coefficient of ±5 ppm/°C) in the remaining three arms the resistance uncertainty of the bridge is 0.01 compared to full bridge configuration containing strain gauge of gauge factor 2.13 ± 1 % is 0.02.

Although temperature drift in the bridge is negligible due to use of precision resistor of low temperature coefficient (±5 ppm/°C), however, effect of temperature can be investigated.