1 Introduction

Nowadays, the Ni-based superalloys have been widely used in the manufacture of gas turbine engine components that are subjected to highly aggressive environment (such as high inlet gas temperatures, high centrifugal loads) in the process of long-term service, and then the creep deformation and stress rupture behavior of these components are important safe limiting factors [1]. For the safety and economic reasons, considerable efforts were exerted to gain a fundamental understanding of creep mechanisms [2]. However, for the high test cost and time-consuming creep test, it is not practicable to carry out extensive experimental investigations to account for all the possible stress–temperature states. Hence, with lower cost and shorter period, it is significant to develop accurate predictions models for simulating creep characteristics. Currently, the traditional methodologies involving power law equations are not sufficient to describe creep behavior in a wide range of stress–temperature conditions [3], which leads to an appearance of more modern techniques such as the Theta projection method [4], the hyperbolic tangent [5] and the Wilshire equations [3]. Up to now, the Wilshire equations developed at Swansea University by Wilshire and Scharning [6] have been validated on predicting typical creep behaviors (i.e., the minimum creep strain rate (\(\dot{\varepsilon }_{\hbox{min} }\)), stress rupture life (t f) and time to a specified creep strain (t ε )) with good extrapolation performance, reasonable temperature capability and availability. The applications were successfully carried out in steel, copper, aluminum alloy and Ni-based polycrystalline superalloy in a wide range of stress–temperature conditions [3, 7]; especially, the modified creep activation energy is close to the lattice self-diffusion energy and breaks seen in the equations are consistent with the observed creep deformation mechanism, which turns to be the physical confidence of this technique. However, validation of this new methodology requires more evidence on its applicability to a wide range of materials, particularly the advanced Ni-based superalloys widely used in the aerospace industry. Meanwhile, compared with the conventional polycrystalline Ni-based superalloys, the directionally solidified (DS) (or single-crystal (SC)) superalloys were developed by eliminating transverse (or any) grain boundaries to provide superior mechanical properties and good corrosion resistance at elevated temperatures. However, the lack of grain boundaries also leads to highly anisotropic material mechanical properties [8], especially in low-cycle fatigue (LCF) and creep behavior [9, 10]. Up to now, the anisotropic creep properties have been investigated adequately by experiments, but little attention was paid to the unified simulation methods for predicting the anisotropic creep behaviors.

In this paper, the capability of Wilshire equations on simulating creep characteristics of typical Ni-based superalloys was verified comprehensively, and then a simple orientation factor defined by ultimate tensile strength (UTS) was introduced to consider the influence of crystal orientation. The physical confidence on this method was also discussed, and the innovative application on Wilshire curves was further carried out with the perspective on full utilization of creep property.

2 Experimental data and analysis

2.1 Experimental data

In this paper, a sufficient amount of experimental creep characteristics data (i.e., \(\dot{\varepsilon }_{\hbox{min} }\), t f and t ε ) were collected for full verifying the feasibility of Wilshire equations, where a wide range of typical Ni-based DS and SC superalloys commonly used in gas turbine applications was adopted (i.e., DS superalloys DZ125 [11, 12], DZ17G [10, 11, 13], DS GTD-111 [14–16] and SC superalloys: CMSX-4 [17–19]). The data at different crystal orientations were also contained for verifying capability of the improved Wilshire method. The detailed data are shown later by the comparison with the master predicted curves. The corresponding experimental procedures can be found from the above-cited literatures. It should be noted that all the mentioned units in this paper are as follows: temperature (T) in K, creep strain rate (\(\dot{\varepsilon }\)) in h−1 and time (t) in h.

2.2 Analysis by traditional power law expression

Since the early 1950s, the most commonly used power law equation for correlating t f with \(\dot{\varepsilon }_{\hbox{min} }\) at high temperatures shown in Eq. (1) was proposed by Monkman and Grant [20]. \(\dot{\varepsilon }_{\hbox{min} }\) described by Dorn equation [21] is shown in Eq. (2):

$$M = t_{\text{f}} \;\dot{\varepsilon }_{\hbox{min} }$$
(1)
$$\dot{\varepsilon }_{\hbox{min} } = A\sigma^{n} \exp ( - Q_{\text{c}} /RT)$$
(2)

where M is material constant and R = 8.314 J·K−1·mol−1, T is Kelvin temperature, A and stress exponent n are material parameters dependent on stress and temperature and Q c is the creep activation energy fitted at constant applied stress (σ). In this section, the above-mentioned power law expression was adopted to predict the stress rupture property of a typical Ni-based DS superalloy DZ125 and the parameter stability was discussed. As shown in Fig. 1a, the stress rupture tests of DZ125 were carried out under a wide range of stress–temperature conditions and the obtained rupture data show obvious temperature and stress dependence. Although the longitudinal (L) direction exhibits overall longer life for each temperature, the anisotropic behavior is pronounced at the lower temperature of 760 °C and is evidently reduced at the higher temperature. The influence of orientation on the stress rupture properties will be uniformly predicted later. It should be noted that, in this paper, the basic assumption is made that the creep rupture behavior is strain controlled and the rupture life is closely connected with \(\dot{\varepsilon }_{\hbox{min} }\) [22]. According to Eqs. (1) and (2), the stress exponents of DZ125 at L direction under different temperatures can be linearly fitted by plotting ln t f versus ln σ. The values calculated by slopes are 14.00 for 760 °C, 5.90 for 850 °C, 5.36 for 900 °C, 5.48 for 980 °C, 4.79 for 1040 °C and 4.60 for 1093 °C, respectively. A roughly decrease in the values of n occurs with the increase in temperature. Meanwhile, the creep activation energy (Q c) of DZ125 can also be calculated at constant applied stress (σ) under variable temperatures, which changes from 509 to 429 kJ·mol−1. That is to say, the parameters n and Q c in Eq. (2) seem to be stress and temperature dependent, which is consistent with the researches on other materials [22]. Hence, the prediction accuracy of the traditional power law expression is accepted only within a limited range of stress and temperature conditions. These intangible variations of the parameters with the change of test conditions make accurate extrapolation of creep properties impossible.

Fig. 1
figure 1

Stress rupture property a and application of UTS-normalized power law equations b of DZ125

Full size image

Subsequently, many studies revealed that the stress dependence on \(\dot{\varepsilon }_{\hbox{min} }\) at different temperatures can be eliminated by normalizing σ through the yield stress (σ yield or UTS (σ TS)) [3]. However, σ TS is usually chosen because it can be carried out with stresses ranging from σ/σ TS = 1 to σ/σ TS = 0. Hence, Eq. (1) evolves into Eq. (3):

$$M/t_{\text{f}} = \dot{\varepsilon }_{\hbox{min} } = A^{ * } (\sigma /\sigma_{\text{TS}} )^{n} \exp ( - Q_{\text{c}}^{ *} /RT)$$
(3)

where A * ≠ A and \(Q_{\text{c}}^{ *}\) are determined by plotting (ln\(\dot{\varepsilon }_{\hbox{min} }\)) or (lnt f) against (1/T) at constant σ/σ TS. The value of \(Q_{\text{c}}^{ *}\) for DZ125 is 302.04 kJ·mol−1. Hence, by plotting ln(σ/σ TS) against \(\ln \left[ {t_{\text{f}} \exp \left( { - Q_{\text{c}}^{*} /\left( {RT} \right)} \right)} \right]\), it can be seen that the stress rupture data of DZ125 (Fig. 1a) at different temperatures are superimposed onto a single curve (Fig. 1b). However, the stress exponent (n) in Eq. (3) is still varied (i.e., ranges from 15.20 to 4.63) with the change of stress level, and once again, this instability of n makes prediction and extrapolation impossible.

3 Estimation of original Wilshire equations

3.1 Original Wilshire equations

According to the above-mentioned application of the traditional power law equations on DZ125, it can be found that the variability in values of n and Q c makes predicting creep properties over a wide range of test conditions difficult. Meanwhile, it should be noted that, for any material, applying a stress equals to σ TS at any given temperature will result in near instantaneous rupture, and creep rupture cannot be expected if the applied stress equals to zero [3]. That is to say, t f → 0 and \(\dot{\varepsilon }_{\hbox{min} } \to \infty\) occur when σ/σ TS → 1, and then t f → ∞ and \(\dot{\varepsilon }_{\hbox{min} } \to 0\) occur as σ/σ TS  → 0. There is no doubt that the stress ranging from 0 to σ TS must be considered in a robust method for predicting creep properties in a wide range of stress conditions. However, when Eq. (3) was rewritten into Eq. (4), it can be seen that this type of power law expression does not meet the basic physical response which occurs with stresses ranging from 0 to σ TS.

$$\sigma /\sigma_{\text{TS}} = \left\{ {M/A^{*} \times \left[ {t_{\text{f}} \exp \left( { - Q_{\text{c}}^{ *} /RT} \right)} \right]^{ - 1} } \right\}^{\frac{1}{n}}$$
(4)

Fortunately, in order to effectively avoids these unpredictable n value variations, the more recently developed Wilshire equations, devised at Swansea University by Wilshire et al. [7], follow the analogous sigmoidal descriptions of creep properties (i.e., \(\dot{\varepsilon }_{\hbox{min} }\), t f and t ε ) to consider the above-mentioned stress variation from 0 to σ TS. The corresponding equations evolved from the traditional power law equations are shown in Eqs. (5)–(7).

$$\frac{\sigma }{{\sigma_{\text{TS}} }} = \exp \left\{ { - k_{1} \left[ {t_{\text{f}} \exp \left( {\frac{{ - Q_{\text{c}}^{ *} }}{RT}} \right)} \right]^{u} } \right\}$$
(5)
$$\frac{\sigma }{{\sigma_{\text{TS}} }} = \exp \left\{ { - k_{2} \left[ {\dot{\varepsilon }_{\hbox{min} } \exp \left( {\frac{{Q_{\text{c}}^{ *} }}{RT}} \right)} \right]^{v} } \right\}$$
(6)
$$\frac{\sigma }{{\sigma_{\text{TS}} }} = \exp \left\{ { - k_{3} \left[ {t_{\varepsilon } \exp \left( {\frac{{ - Q_{\text{c}}^{*} }}{RT}} \right)} \right]^{w} } \right\}$$
(7)

where the parameters \(Q_{\text{c}}^{*}\), k 1, k 2, k 3, u, v and w are derivable from a reasonably comprehensive set of creep rupture data. Although the capability of the Wilshire equations was proved in many materials, few applications were carried out on the advanced Ni-based superalloys. Hence, the validity of Wilshire equations was carefully proved on DZ125 as follows.

3.2 Prediction results

To illustrate the capability of this model, the activation energy (\(Q_{\text{c}}^{*}\)) should be firstly estimated by plotting ln\(\dot{\varepsilon }_{\hbox{min} } \) or lnt f against 1/T at constant σ/σ TS, which ensures that \(Q_{\text{c}}^{ *}\) remains constant regardless of testing temperature. Concretely, the values of \(Q_{\text{c}}^{ *}\) are 302.04, 307.93 and 262.1 kJ·mol−1 for DZ125, DS GTD-111 and CMSX-4, respectively. Then, the remaining constants in each equation can be further determined by linear fitting. For example, by plotting \(\ln [t_{\text{f}} \exp ( - Q_{\text{c}}^{*} /RT)]\) against ln[−ln(σ/σ TS)], the constants u and k 1 can be calculated by the gradient and intercept. Finally, the predicted creep properties at different test conditions are compared with the experimental data published in cited literatures. The validation of Wilshire equations was carried out on \(\dot{\varepsilon }_{\hbox{min} }\), t f and t ε , respectively.

3.2.1 Stress rupture life \((t_{\text{f}})\)

By plotting \(\ln [t_{\text{f}} \exp ( - Q_{c}^{*} /RT)]\) against ln[−ln(σ/σ TS)], the predicted stress rupture lives under different testing conditions of DZ125 are shown in Fig. 2a, from which it can seen that t f (obtained in a wide range of testing conditions) of DZ125 can be well described by Wilshire equations. The predicted master curves are interrupted into two continuous lines, and the physical basic for the predicted break points by this method will be discussed in detail later. For DZ125, the values of u and k 1 are 0.134 and 28.6 for σ/σ TS < 0.448, while 0.203 and 178.0 for σ/σ TS > 0.448. The predicted stress rupture lives at transverse (T) direction by the improved method are also exhibited in Fig. 2 but will be discussed later.

Fig. 2
figure 2

Creep properties of DZ125 predicted by Wilshire method: a stress rupture life, b minimum creep strain rate, c time to creep strain (ε = 2 %) and d time to creep strain (ε = 5 %)

Full size image

3.2.2 Minimum creep strain rate (\(\dot{\varepsilon }_{\hbox{min} }\))

Once again, the constants v and k 2 in Eq. (6) can also be calculated easily by the gradient and intercept in the plot of \(\ln [\dot{\varepsilon }_{\hbox{min} } \exp (Q_{\text{c}}^{*} /RT)]\) against ln[−ln(σ/σ TS)]. As shown in Fig. 2b, it can be concluded that \(\dot{\varepsilon }_{\hbox{min} }\) of DZ125 can be well predicted. Compared with Fig. 2a, it is encouraging that the break point locates at the same level of σ/σ TS. The values of v and k 2 are –0.111 and 11.37 for σ/σ TS < 0.448, whereas they are −0.152 and 30.87 for σ/σ TS > 0.448.

3.2.3 Time to a specified strain (t ε )

To predict the time to a specified creep strain, similar prediction was carried out by plotting \(\ln [t_{\varepsilon } \exp ( - Q_{\text{c}}^{*} /RT)]\) against ln[−ln(σ/σ TS)]. As shown in Fig. 2c, d, the needed t ε to reach two specified creep strains of DZ125 is well described, where similar locations of break points also exist as before. When the specimens are crept to 2 % strain, the values of w and k 3 are 0.106 and 17.2 for σ/σ TS < 0.448, while 0.125 and 29.5 for σ/σ TS > 0.448. When the specimens are even crept to a bigger strain of 5 %, the needed time can also be well predicted and the values of w and k 3 are 0.127 and 26.55 for σ/σ TS < 0.448, while 0.154 and 56.03 for σ/σ TS > 0.448.

4 Improved Wilshire equations

It was proved that the creep properties along a specified crystal direction of DZ125 (i.e., L direction) can be well simulated by the original Wilshire equations. However, the creep properties of DS and SC superalloys are inherently anisotropic [23]. Up to now, the Wilshire equations have not been further conducted for predicting anisotropic creep characteristics uniformly, which turns to be the other purpose of this article. To consider the influence of orientation on \(\dot{\varepsilon }_{\hbox{min} }\), Guo et al. reported that the anisotropic \(\dot{\varepsilon }_{\hbox{min} }\) was due to the elastic anisotropy, and then Eq. (2) turns to be Eq. (8) as follows [13]:

$$\dot{\varepsilon }_{\hbox{min} } = B(\sigma /E)^{n} \exp ( - Q_{\text{c}} /RT)$$
(8)

where B is the material parameter, E is the Young’s modulus and Q c is assumed to be orientation independent. They found that the anisotropic behavior of \(\dot{\varepsilon }_{\hbox{min} }\) can be well described by this simply modified equations. Although this equation was validated in a limited stress–temperature condition, it is encouraged to assume that the anisotropic creep properties are consistent with orientation-related material property parameter. According to the orientation dependence on t f of DZ125 with the increase in temperature as shown in Fig. 1a, it can be concluded that in a wide range of stress-temperature conditions, the anisotropic t f exhibits better consistency with UTS (Fig. 3a) rather than Young’s modulus (Fig. 3b). Hence, it is assumed that the influence of crystal orientation on creep properties can be simply considered by the compensation function of UTS. Concretely, \(\dot{\varepsilon }_{\hbox{min} }\) in any crystal orientation [hkl] is supposed to be described by the introduction of an orientation factor, f(A hkl ) = σ TS,[001]/σ TS,[hkl], then Eq. (8) now becomes:

$$f(A_{hkl} ) = \sigma_{{{\text{TS}},[001]}} /\sigma_{{{\text{TS}},[hkl]}}$$
(9)
$$\dot{\varepsilon }_{\hbox{min} } = C(f(A_{hkl} )\sigma )^{n} \exp ( - Q_{\text{c}} /(RT))$$
(10)

where A hkl is the orientation factor, σ TS,[001] is UTS at [001] orientation, σ TS,[hkl] is UTS at one crystal orientation [hkl] and C is material parameter. By plotting \(\ln\dot{\varepsilon }_{\hbox{min} }\) against ln[f(A hkl )σ] as shown in Fig. 4, it can be concluded that, to a certain extent, the anisotropic \(\dot{\varepsilon }_{\hbox{min} }\) of DZ17G and DS GTD-111 at different temperatures can be well described by Eqs. (9) and (10). Subsequently, following the same evolution from Eq. (1) with help of Eq. (2) to the original Wilshire equations, the orientation factor modified Wilshire equations are now shown as follows:

$$\frac{\sigma }{{\sigma_{\text{TS}} }} = \exp \left\{ { - k_{1} \left[ {f(A_{hkl} )t_{\text{f}} \exp \left( {\frac{{ - Q_{\text{c}}^{ *} }}{RT}} \right)} \right]^{u} } \right\}$$
(11)
$$\frac{\sigma }{{\sigma_{\text{TS}} }} = \exp \left\{ { - k_{2} \left[ {f(A_{hkl} )\dot{\varepsilon }_{\hbox{min} } \exp \left( {\frac{{Q_{\text{c}}^{*} }}{RT}} \right)} \right]^{v} } \right\}$$
(12)
$$\frac{\sigma }{{\sigma_{\text{TS}} }} = \exp \left\{ { - k_{3} \left[ {f(A_{hkl} )t_{\varepsilon } \exp \left( {\frac{{ - Q_{\text{c}}^{*} }}{RT}} \right)} \right]^{w} } \right\}$$
(13)

where the parameters \(Q_{\text{c}}^{ *}\) are also assumed to be orientation independent, all parameters are calculated in the same way as those in Eq. (5).

Fig. 3
figure 3

Material properties of DZ125 at different temperatures: a UTS and b Young’s modulus

Full size image
Fig. 4
figure 4

Schematic expressed by ln\(\dot{\varepsilon }_{\hbox{min} }\) versus ln[f(A hkl )σ]

Full size image

Similarly, the predicted master curves of anisotropic creep properties by the improved Wilshire equations are compared with collected testing data of a Ni-based superalloy DS GTD-111. Using the same procedure as before, the simulated anisotropic creep results of DZ125 and DS GTD-111 are shown in Figs. 2a, 5 and 6, respectively. It can be seen that a very good simulation of the anisotropic creep characteristics of DS GTD-111 (i.e., \(\dot{\varepsilon }_{\hbox{min} }\), t f and t ε ; i.e., ε = 0.3 %, 0.5 % and 1.0 %) is obtained by the improved Wilshire equations. The values of the model parameters in Eq. (11) are shown in Figs. 2a, 5 and 6.

Fig. 5
figure 5

Schematic expressed by a \(\ln [f\left( {A_{hkl} } \right)t_{\text{f}} \exp ( - Q_{\text{c}}^{*} /RT)]\) versus ln[−ln(σ/σ TS)] and b \(\ln [f\left( {A_{hkl} } \right)\dot{\varepsilon }_{\hbox{min} } \exp ( - Q_{\text{c}}^{*} /RT)]\) versus ln[−ln(σ/σ TS)] of DS GTD-111

Full size image
Fig. 6
figure 6

Schematic expressed by \(\ln [f\left( {A_{hkl} } \right)t_{\varepsilon } \exp ( - Q_{\text{c}}^{*} /RT)]\) versus ln[−ln(σ/σ TS)] of DS GTD-111: a 0.3 % strain, b 0.5 % strain, and c 1.0 % strain

Full size image

5 Discussions

5.1 Physical significance of \(Q_{\text{c}}^{ *}\)

The physical significances of the model parameter \(Q_{\text{c}}^{ *}\) of Wilshire equations are discussed to provide confidence to this method. The values of \(Q_{\text{c}}^{ *}\) are calculated from the superimposition of different temperature data sets from temperature compensated graphs of either t f or \(\dot{\varepsilon }_{\hbox{min} }\) against normalized stress σ/σ TS at each testing temperature, and previous work for a range of materials shows that this processing method provides more realistic and constant activation energy values, which compare favorably with the activation energy for lattice diffusion [24]. For the Ni-based superalloys investigated in this paper, as mentioned before, the values of \(Q_{\text{c}}^{*}\) are 302.04, 307.93 and 262.10 kJ·mol−1 for DZ125, DS GTD-111 and CMSX-4, respectively. The \(Q_{\text{c}}^{*}\) value of DZ125 is much lower than Q c (i.e., ranging from 509 to 429 kJ·mol−1) calculated by traditional power law expressions. Meanwhile, it is reported that the self-diffusion activation energy for Ni-based superalloys is in the range of 257–283 kJ·mol−1 [25]. Hence, these obtained values are far closer to the activation energy for lattice diffusion of Ni-based superalloys than the Q c values calculated traditionally.

5.2 Physical significance of predicted break points

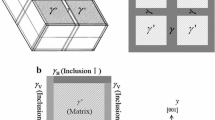
It is proved that the existed ‘break point’ in the graph by plotting Wilshire equations is related to the transition of creep deformation mechanism which occurs at high and low regions of σ/σ TS, which largely helps to provide confidence to this method [3]. Currently, during the procedure of predicting t f or \(\dot{\varepsilon }_{\hbox{min} }\) of SC superalloy CMSX-4, predicted break points are compared with the stress-level related creep mechanism published in Ref. [26]. As shown in Fig. 7a, the stress rupture data tested in a wide range of stress–temperature conditions of CMSX-4 at [001] direction were simulated, and once again, two break points clearly exist at different stress levels (i.e., σ/σ TS = 0.26 and 0.51). Meanwhile, as shown in Fig. 7b, the creep deformation mechanism of CMSX-4 was investigated systematically before [26]. Three regimes are identified, and distinct microstructural degradation is predominant for each mode. Firstly, the specimens crept at low temperatures with high applied stress exhibit primary mode, whose characteristic is a significant heterogeneity of slip and the deformation is controlled by the movement of dislocation ribbons of net Burgers vector \(a < 11\bar{2} >\). Secondly, the tertiary mode occurs in the intermediate creep regime, where the dislocation activity of the \(a/2 < 1\bar{1}1 > \left\{ {111} \right\}\) type is restricted to the γ channels between the γ′ particles. The density of dislocations is found to increase with the increase in creep strain. Thirdly, the rafting mode happens at high temperature with low applied stress, where the γ/γ′ microstructure degrades rather quickly for thermally activated processes are favored strongly. Fortunately, as shown in Fig. 7b, it is encouraging that different temperature–stress conditions required for the operation of these three modes in CMSX-4 are well simulated through the predicted break points (i.e., located at σ/σ TS = 0.26 and 0.51) by Wilshire equations.

Fig. 7
figure 7

Schematic expressed by \(\ln [t_{\text{f}} \exp ( - Q_{\text c}^{*} /RT)]\) versus ln[−ln(σ/σ TS)] a and modes of creep deformation at different temperature–stress conditions b of CMSX-4 in [001] direction

Full size image

5.3 Further application of Wilshire equations

It is well known that the traditional Larson–Miller curve is widely used for appraising the stress rupture strength of different materials. This method is based on the concept of absolute stress to compare the creep properties. However, it is insufficient to only evaluate the creep properties of different materials from the perspective of absolute performance. Actually, in order to increase the safety factor and save costs, the engineers and designers are always looking forward to fully knowing the potential on creep properties of the adopted materials. It is easy to understand that when the same stress rupture life of two materials is satisfied simultaneously (at the same temperature), the material crept at a lower stress level normalized by UTS (σ/σ TS) will be the safer choice. On the other hand, when the two materials are crept at the same σ/σ TS (at the same temperature), the material with a longer rupture life will be the more economical choice for designers. Hence, in this section, it is tried to evaluate the creep properties of different materials from the perspective of relative performance to make full use of materials. Fortunately, it is obvious that one inherent property of the Wilshire equations is that the applied stress is normalized by UTS; especially, the superior prediction and extrapolation performance of this method are fully proved in a wide range of materials, and hence, a valuable alternative technique (named as Wilshire curve) to evaluate the creep properties in an innovative perspective is proposed here. For the first time, this new technique is conducted here for evaluating the stress rupture life of two typical DS Ni-based superalloys (i.e., DZ125 and DZ17G at L direction), and the Larson–Miller parametric method is conducted simultaneously for comparison. The Larson–Miller parameter is described as P = T(20 + lgt)/1000, where T is the temperature in K and t is the stress rupture lifetime in h. The applied stress can be expressed using a polynomial of degree 3: lgσ = \(a_{0 } + a_{1} P + a_{2} P ^{2} + a_{3} P^{3}\), where the parameters a 0, a 1, a 2, a 3 are fitted by testing data. As shown in Fig. 8a, the experimental data (i.e., applied stress vs. Larson–Miller parameter) of DZ125 and DZ17G are well fitted, which agrees with the conclusion that the Larson–Miller method gets good accuracy in predicting creep properties in a limit region of stress rupture life. The values of a 0–a 3 of DZ125 are −6.283, 1.108, −0.0408 and 0.000434, and they are −11.83, 1.734, −0.0643 and 0.000724 for DZ17G, respectively. As mentioned above, the parameters in Eq. (5) of Wilshire method can be fitted linearly by plotting \(\ln [t_{\text f} \exp ( - Q_{c}^{*} /RT)]\) against ln[−ln(σ/σ TS)]. For DZ125, the values of u and k 1 are 0.134 and 28.6 for σ/σ TS < 0.448, while 0.203 and 178 for σ/σ TS > 0.448. For DZ17G, the values of u and k 1 are 0.174 and 40.3 for σ/σ TS < 0.397, while 0.239 and 165.8 for σ/σ TS > 0.397. As shown in Fig. 8b, using the values of parameters, the stress rupture master curves can be plotted by Eq. (5) (x-axis is \(t_{\text{f}} { \exp }( - Q_{c}^{*} /RT)\), and y-axis is the relative stress (σ/σ TS)), which exhibits good accuracy. However, our attention is not paid to the predicting ability of these two methods. We are encouraged to find that these two methods provide entirely different creep rupture performances. In Fig. 8a, the vertical axis is the absolute stress and DZ125 owns overall better creep rupture properties, but this superiority obviously decreases with the increase in P parameter. Conversely, when the vertical axis in Fig. 8b is the relative stress (i.e., UTS-normalized stress), the DZ17G owns entirely better creep rupture properties. That is to say, this simple but robust method developed by Wilshire and co-workers can be further used for evaluating creep properties (also including \(\dot{\varepsilon }_{\hbox{min} }\) and t ε ) of different materials with an innovative perspective on making full use of creep properties.

Fig. 8
figure 8

Comparison of stress rupture properties of DZ125 and DZ17G by a Larson–Miller curve and b Wilshire curve

Full size image

6 Conclusion

In this paper, the capability of Wilshire equations in simulating typical creep characteristics in typical anisotropic Ni-based DS and SC superalloys was fully verified. Some principal conclusions are listed as follows. The obtained creep activation energy (\(Q_{\text{c}}^{ *}\)) by Wilshire method is far closer to the activation energy for lattice diffusion of Ni-based superalloys than the value calculated traditionally. The flexibility of the orientation factor modified Wilshire equations is fully demonstrated by various data sets of DZ125 and DS GTD-111, where good simulations of the anisotropic t f, \(\dot{\varepsilon }_{\hbox{min} }\) and t ε are obtained.

The obtained ‘break point’ stress by Wilshire method is well consistent with the transition of creep deformation mechanism of CMSX-4 happened at different temperature–stress regions, which helps to provide physical confidence of this method. The Wilshire method is further used for evaluating typical creep properties of different materials with an innovative perspective on making full use of creep properties.