1 Introduction

Safe and soft landing on a celestial body (planet, moon, asteroid, comet) has been and will be a central objective for space exploration. For current and future missions, pin-point landings are planned which require a high accuracy in absolute navigation. This is achieved by combining inertial measurements and measurements from optical sensors like star trackers, laser altimeters and processed navigation camera images. This combination of sensors is common to many missions. When neglecting cooperative targets such as landing sites equipped with beacons, only special image processing methods (for camera and LIDAR images) can provide absolute position and/or attitude information within the local reference frame of the target celestial body. Different methods for determining the absolute position are investigated. They all base on the identification of unique feature or landmarks in the images recorded by a navigation camera.

Within the scope of the program Autonomous Terrain-based Optical Navigation (ATON) of the German Aerospace Center (DLR), several algorithms, techniques and architectures have been investigated, further developed and tested in hardware-in-the-loop tests and helicopter flight tests. The development results of ATON include methods for feature-based tracking and SLAM [2], 3D terrain reconstruction from images, 3D matching, shadow matching [5], crater navigation [7, 8] as well as sensor data fusion [1] of the different pre-processed outputs with data of an inertial measurement unit (IMU), laser altimeter, and star tracker.

This paper focuses on the fusion of absolute position and attitude information from navigation camera images with IMU measurements. Section 2 introduces the crater navigation method. In Sect. 3, the hybridization with IMU measurements is presented. Sections 4 and 5 explain the test setup of the flight tests, present and discuss the test results.

2 Optical navigation by crater detection

The crater navigation method is the only source of absolute position measurements supporting the navigation filter during these flight experiments. Crater detections within images of a navigation camera, matched to a database of known craters within the world reference frame, allow the straightforward solution for the pose of the capturing camera w.r.t. the global reference frame and, by extension, of the vehicle to which it is fixed.

Most crater navigation schemes suggested in the literature function in a prediction-match-update configuration, where the burden of matching detected image craters to known database craters is removed by providing prior knowledge of the vehicle pose, enabling direct visual matching within the image space: prior pose knowledge allows projecting the crater database into the image, where proximity and size matching of the projections to the detections can then be performed. Basically, all crater detection methods can be employed in this way.

A requirement not satisfied by such a prediction-match-update setup is the capability of zero knowledge initialization, also known as the “Lost in Space” scenario, which we define as any situation where the prior pose knowledge is insufficient to derive an unambiguous match between detections and crater database in the way described in the last paragraph.

This situation occurs during our flight experiments when the crater targets first enter the view of the helicopter drone at the start of the descent trajectory (cf. Sect. 4). At that point in time, the navigation filter is still uninitialized and, therefore, unable to provide useful prior knowledge that would enable an image space matching. At this point, we employ the CNav software in its “Lost in Space” mode to provide an initial pose for initialization of the navigation filter. Afterwards, predictions from the filter aid the crater detector in tracking previous solutions for improved performance.

The crater detection method employed is an algorithm developed at DLR in Maass [7, 8]. The core characteristic of our crater detection algorithm (CDA) is that it is based on the image processing technique known as segmentation, as opposed to methods that rely on in-image edge detection or parameter space transforms (e.g., Hough transform).

Edge-based CDAs are an earlier detection method and have been pioneered by Cheng et al. (cf. [3] and references therein), but they either require computationally expensive scale space analysis of the image to satisfy their underlying assumptions or risk being limited to detecting craters of very limited scale range. Segmentation-based CDAs do not have to suffer from this limitation. In this class of methods, beyond our own, algorithms have been developed by Spigai, Simard Bilodeau et al. [11, 12], who employ distance and watershed transforms to extract high-contrast areas in image of the lunar surface that represent parts with deep shadow or high reflection within craters. Our approach on the other hand is largely similar to the MSER image feature detector [9], but with alternative and simpler stability criteria to reduce computational complexity and avoid costly convexity tests. In the following, we will quickly summarize the basic functionality principle of our CDA.

In an input camera image of the lunar surface (or that of any other surface with impact craters and little variation in reflectance, i.e., texture), our method extracts neighboring illuminated and shadowed sections that are characteristic of impact craters. Departing from the example Fig. 1a, we extract stable connected regions of above- and below-average intensity, as shown in Fig. 1b, c.

Fig. 1
figure 1

Extracting illuminated and shadowed areas from an image of the lunar surface

Full size image

The centroids traced in the Fig. 1b, c serve to compute stability criteria for the extracted areas, as is performed in MSER by tracking of the connected areas of the image support and their respective area and margin length. Conceptually, this is accomplished by iteratively segmenting binary images of the input image for a sequentially rising threshold. This is illustrated in Fig. 2 for the crater just left of the image center of the example Fig. 1a. In Fig. 2a, we see a small subset of binary images for a rising threshold with the corresponding connected areas of the image support being shown in Fig. 2b. The color-coding used in the figure is green for a tracked shadowed area of the image and red for a tracked illuminated area, with the lighter green and red shades indicating the respective endpoint areas of the tracking chain. The center field of Fig. 2b symbolizes the point at which the tracked areas stop being isolated and the tracked centroids jump.

Fig. 2
figure 2

Sequential extraction of connected areas of contrast for a single crater with centroid movement as stability measure

Full size image

Extracted stable illuminated and shaded areas like the ones marked light green and light red in Fig. 2b are paired by proximity and by configuration with respect to a global illumination direction. This illumination direction is deduced from the direction histogram of a directed graph connecting the centroids of mutually closest extracted areas of similar size, with edges running from shadowed to illuminated areas’ centroids. The graph for the example image is shown in Fig. 3a and the resulting histogram is shown in Fig. 3b. Those edges of the graph whose direction agrees with the histogram peak up to a tolerance indicate correct pairings and the corresponding areas are used to fit principal components ellipses over the union of their constituent image support points, as shown in Fig. 3c. For details of this process, please refer to [7].

Fig. 3
figure 3

Illumination direction recovery from directed proximity graph over all extracted area centroids used to form candidate ellipses

Full size image

In our experiments, we use the camera image without preprocessing or filtering (except for undistortion) and the final candidates from Fig. 3c are used without further postprocessing. This makes the algorithm very simple and keeps the computational load low.

The detections within the image are assigned to a static catalog (fixed in the world reference coordinates, cf. Sect. 3.1). This correspondence table between a set of image coordinates and the set of global crater database entries forms the input to recovering the pose of the camera that captured the processed image with respect to the crater database’s coordinate system.

To retain simplicity and deterministic runtimes, we choose the well-known EPnP algorithm [6] in conjunction with the QCP solver [14]. Output of the processing chain described here is an attitude quaternion \(\mathbf {q}^M_C\) (cf. Sect. 3.6.2) and a cartesian position vector \(\mathbf {r}^M\) of the camera’s focal point within the reference frame.

One noteworthy property of EPnP algorithm is that it only solves for the spatial rotation of the detected vs. the known craters. The translational part of the transformation is directly computed from this rotation together with the crater database point cloud and its scale, so it is to be expected that errors in the position measurements correlate strongly with those in the rotation measurement. The effective number of degrees of freedom in the errors of the seven measurement elements (four of the quaternion, three of the position) should, therefore, be three. We will investigate for this behaviour when analyzing the error data in Sect. 5.1.

3 Hybridization with inertial measurements

The proposed hybrid navigation system architecture is as shown in Fig. 4. The CNav system provides the navigation computer with position and attitude fixes. In turn, the navigation algorithm uses these in a Kalman filter to correct the inertial (or strapdown) propagation running in parallel. Formally, this is equivalent to a loosely coupled hybrid system implemented in closed-loop, i.e., where the sensor fusion routine frequently corrects the inertial integration. Its states are then reset. This is a modular approach in the sense that the filter and inertial propagation run independently in parallel. The filter estimates error states rather than full states in a so-called indirect filtering scheme. One of the advantages of this setup is the limited state growth granted by the frequent state resets, which minimizes potential linearization errors. The feedback and explicit estimation of IMU perturbations further increases robustness and improves free-inertial propagation performance (in between CNav fixes). Modularity also allows dual-frequency operation; in the present case, the inertial propagation runs at 100 Hz (IMU output rate), while the filter is propagated at 10 Hz. The filter is updated asynchronously whenever a measurement CNav is available (cf. Sect. 4.1).

Fig. 4
figure 4

Hybrid optical/inertial navigation diagram

Full size image

3.1 Reference frames

In the derivation and implementation of the hybrid navigation system at hand, the following reference frames are employed:

  • A planet centred frame, M, is used to write the kinematics state (position, velocity and attitude). Given the Earthly test scenario presented in this work (cf. Sect. 4), the system version here described uses the ECEF frame for all instances of frame M. In a moon scenario, M would be instead a moon-centred moon-fixed (MCMF) frame.

  • An inertial frame, denoted I, is used to support the definition and handling of absolute physical quantities (e.g., measurements of inertial sensors). It is here defined as being aligned with M frame for mission time \(t = 0\) s, i.e., when the system is turned on.

  • A body reference frame, B, is defined as being centered in the inertial measurement unit (IMU) and fixed to the vehicle. In the case of the tested configuration, the body axes were aligned as: x along the longitudinal direction of the vehicle pointing forward, z along the vehicle’s vertical direction pointing down, and y forming an orthogonal right-handed frame.

  • A camera fixed reference frame, C, is defined as the right-handed cartesian coordinate system centered at the camera’s focal point, with the z axis being the optical axis, the x axis pointing left and the y axis pointing up in the image.

3.2 Time indexing

As previously mentioned, the inertial propagation and the fusion filter run in parallel at different rates. The former runs at high-rate (HR 100 Hz) and the latter at low-rate (LR 10 Hz). The time index of the HR tasks is denoted j and that of the LR ones is k. The index j is reset at each LR step, \(t_k = t_{j=0} ,\) being \(t_{k+1} = t_{j=N}\) , with \(N = 10\).

3.3 Inertial propagation

The vehicle body attitude w.r.t. M frame is represented using the quaternion \({\mathbf q}_{B}^{M}\), given as:

$$\begin{aligned} {\mathbf q}_{B_{j+1}}^{M_{j+1}} = {\mathbf q}^{B_j}_{B_{j+1}} {\mathbf q}_{B_j}^{M_j} {\mathbf q}_{M_j}^{M_{j+1}} , \end{aligned}$$
(1)

and updated using the gyroscope measurements and a third-order algorithm [10]

$$\begin{aligned} {\mathbf q}^{B_j}_{B_{j+1}} = \begin{bmatrix}\left( -\frac{1}{2}{\mathbf {I}}+\frac{1}{48}\Vert \varvec{\varDelta } \varvec{\theta } ^B_{j+1}\Vert ^2{\mathbf {I}}+\frac{1}{24}[{\varvec{\varDelta } \varvec{\theta } ^B_{j}}\right) ]\varvec{\varDelta } \varvec{\theta } ^B_{j+1}\\ 1-\frac{1}{8}\Vert \varvec{\varDelta } \varvec{\theta } ^B_{j+1}\Vert ^2\end{bmatrix} , \end{aligned}$$
(2)

where \(\bigl [\varvec{\varDelta } \varvec{\theta } ^B_{j} \times \bigr ]\) is the skew-symmetric matrix of \(\varvec{\varDelta } \varvec{\theta } ^B_{j}\). \({\mathbf {I}}\) is a 3 \(\times\) 3 identity matrix.

The translational kinematics can be written in M frame as:

$$\begin{aligned} {\mathbf v}_{j+1}^{M}&= -\varvec{\varOmega } _{IM}^M{\mathbf r}_{j+1}^M+{\mathbf C}_{M_j}^{M_{j+1}}({{\mathbf v}_j^M+\varvec{\varOmega } _{IM}^M{\mathbf r}_j^M}) +{\mathbf C}_{I}^{M_{j+1}}\varvec{\varDelta } {\mathbf v}^I_{j+1} \end{aligned}$$
(3)
$$\begin{aligned} {\mathbf r}_{j+1}^M&= {\mathbf C}_{M_j}^{M_{j+1}}{\mathbf r}_j^M+{\mathbf C}_{I}^{M_{j+1}}\varvec{\varDelta } {\mathbf r}_{j+1}^I , \end{aligned}$$
(4)

where \(\varvec{\varOmega } _{IM}^M = [\varvec{\omega } _{IM}^M\times ]\), i.e., the skew-symmetric matrix of the planet’s absolute angular velocity in M coordinates. The inertial position and velocity integrals \(\varvec{\varDelta } {\mathbf r}^I_{j+1}\) and \(\varvec{\varDelta } {\mathbf v}^I_{j+1}\) can be given as:

$$\begin{aligned} \varvec{\varDelta } {\mathbf v}^I_{j+1}&= \varvec{\varDelta } {\mathbf v}^I_{\mathsf {sf},j+1}+\varvec{\varDelta } {\mathbf v}^I_{\mathsf {g},j+1} , \end{aligned}$$
(5)
$$\begin{aligned} \varvec{\varDelta } {\mathbf r}^I_{j+1}&= \Delta t_{j+1}{\mathbf C}_{M_j}^{I}({{\mathbf v}_j^M+\varvec{\varOmega } _{IM}^M{\mathbf r}_j^M}) \nonumber \\&\quad + \frac{\Delta t_{j+1}}{2}({\varvec{\varDelta } {\mathbf v}^I_{\mathsf {sf},j+1}+\varvec{\varDelta } {\mathbf v}^I_{\mathsf {g},j+1}}) , \end{aligned}$$
(6)

where \(\varvec{\varDelta } {\mathbf r}^I_{j+1}\) was obtained through a trapezoidal scheme with \(\Delta t_{j+1}\) being the time interval from step j to \(j+1\). The velocity integral was split into a gravitational component and a specific force one.

The former is here computed at the midpoint of the time step as:

$$\begin{aligned} \varvec{\varDelta } {\mathbf v}_{\mathsf {g},j+1}^{I}&= \int ^{t_{j+1}}_{t_j}{{\mathbf g}^I}\mathsf {d}t\nonumber \\&\approx \Delta t_{j+1} {\mathbf C}_{M_{j+\frac{1}{2}}}^{I}{\mathbf g}_{j+\frac{1}{2}}^{M}\nonumber \\&\approx \Delta t_{j+1}\;{\mathbf C}_{M_{j+\frac{1}{2}}}^{I}{\varvec{{g}}}^M\left( {\mathbf r}_{j+\frac{1}{2}}^{M}\right) \nonumber \\&\approx \Delta t_{j+1}\;{\mathbf C}_{M_{j+\frac{1}{2}}}^{I}{\varvec{{g}}}^M\left( {\mathbf C}_{M_j}^{M_{j+\frac{1}{2}}}\left( {\mathbf r}_j^M+\frac{\Delta t_j}{2}{\mathbf v}_j^M\right) \right) , \end{aligned}$$
(7)

where \({\varvec{{g}}}^M(\,\cdot \,)\) is the gravity acceleration model in M frame.

The specific force Delta-V, measured by the accelerometer, is also assumed to be taken at the time-step midpoint to account for the body rotation during such interval. It is

$$\begin{aligned} \varvec{\varDelta } {\mathbf v}_{\mathsf {sf},j+1}^I \approx {\mathbf C}_{M_j}^{I}{\mathbf C}_{B_j}^{M_j}{\mathbf C}_{B_{j+\frac{1}{2}}}^{B_j}\varvec{\varDelta } {\mathbf v}^B_{j+1} , \end{aligned}$$
(8)

where \(\varvec{\varDelta } {\mathbf v}^B_{j+1}\) is the accelerometer integrated measurement from \(t_j\) to \(t_{j+1}\).

3.4 Filter algorithm

As previously mentioned the filter used estimates error states; it is, in fact, an error state extended Kalman filter (eEKF) as the one used in [13].

The whole-state and measurement system is modeled as:

$$\begin{aligned} {\mathbf x}_{k+1}&= {\varvec{\phi }} _k({\mathbf x}_k)+{\mathbf w}_k ,\end{aligned}$$
(9)
$$\begin{aligned} {\mathbf y}_k&= {\varvec{{h}}}_k({\mathbf x}_k)+\varvec{\nu } _k , \end{aligned}$$
(10)

where \({\mathbf w}_k\sim \mathcal {N}({\varvec{0}},{\mathbf Q}_k)\) and \(\varvec{\nu } _k\sim \mathcal {N}({\varvec{0}},{\mathbf R}_k)\) are process and measurement noises, respectively.

The error state system and measurement models are

$$\begin{aligned} \varvec{\delta } {\mathbf x}_{k+1}&= {\mathbf x}_{k+1} - \hat{{\mathbf x}}_{k+1} = {\varvec{\phi }} _k(\hat{{\mathbf x}}_k+\varvec{\delta } {\mathbf x}_k)-{\varvec{\phi }} _k(\hat{{\mathbf x}}_k)+{\mathbf w}_k ,\end{aligned}$$
(11)
$$\begin{aligned} \varvec{\delta } {\mathbf y}_k&= {\mathbf y}_k - \hat{\mathbf y}_k = {\varvec{{h}}}_k(\hat{{\mathbf x}}_k+\varvec{\delta } {\mathbf x}_k)-{\varvec{{h}}}_k(\hat{{\mathbf x}}_k)+\varvec{\nu } _k , \end{aligned}$$
(12)

where \(\hat{\mathbf x}\) is the estimated whole-state vector.

The covariance of the error state is propagated as:

$$\begin{aligned} {\mathbf P}_{k+1}&= E\{{({\varvec{\delta } {\mathbf x}_{k+1}-\varvec{\delta } \hat{\mathbf x}_{k+1}})({\varvec{\delta } {\mathbf x}_{k+1}-\varvec{\delta } \hat{\mathbf x}_{k+1}})^{{\mathsf {T}}}} \} \nonumber \\&\approx {\varvec{\varPhi }} _kE\{{({\varvec{\delta } {\mathbf x}_k-\varvec{\delta } \hat{\mathbf x}_k})({\varvec{\delta } {\mathbf x}_k-\varvec{\delta } \hat{\mathbf x}_k})^{{\mathsf {T}}}} \} {\varvec{\varPhi }} _k^{{\mathsf {T}}}+ E\left\{ {\mathbf w}_k{\mathbf w}_k^{{\mathsf {T}}}\right\} \nonumber \\&\approx {\varvec{\varPhi }} _k{\mathbf P}_k{\varvec{\varPhi }} _k^{{\mathsf {T}}}+ {\mathbf Q}_k , \end{aligned}$$
(13)

with the Jacobian of the transition function \({\varvec{\phi }}\) defined as:

$$\begin{aligned} {\varvec{\varPhi }} _k = \frac{{\partial }{\varvec{\phi }} _k\left( {\mathbf x}_k\right) }{{\partial }{\mathbf x}_k}\Biggl .\Biggr |_{{\hat{\mathbf x}_k}} . \end{aligned}$$
(14)

The covariance \({\mathbf S}\) of the error measurement residual is given by

$$\begin{aligned} {\mathbf S}_k = E\{{({\varvec{\delta } {\mathbf y}_k-\varvec{\delta } \hat{\mathbf y}_k})({\varvec{\delta } {\mathbf y}_k-\varvec{\delta } \hat{\mathbf y}_k}^{{\mathsf {T}}}})\} \approx {\mathbf H}_k{\mathbf P}_k{\mathbf H}_k^{{\mathsf {T}}}+ {\mathbf R}_k , \end{aligned}$$
(15)

where the estimated error measurement is

$$\begin{aligned} \varvec{\delta } \hat{\mathbf y}_k={\varvec{{h}}}_k(\hat{{\mathbf x}}_k+\varvec{\delta } \hat{\mathbf x}_k)+{\varvec{{h}}}_k(\hat{{\mathbf x}}_k) , \end{aligned}$$
(16)

and \({\mathbf H}\) is the Jacobian of the error measurement model (10), given that the relation between whole- and error states in (11) obeys

$$\begin{aligned} {\mathbf H}_k = \frac{{\partial }\varvec{\delta } {\mathbf y}_k}{{\partial }\varvec{\delta } {\mathbf x}_{k}}\Biggl .\Biggr |_{{\varvec{\delta } \hat{\mathbf x}_{k},\hat{\mathbf x}_k}} =\frac{{\partial }{\varvec{{h}}}_k({\mathbf x}_k)}{{\partial }{\mathbf x}_k}\Biggl .\Biggr |_{{\hat{\mathbf x}_k}} . \end{aligned}$$
(17)

When a measurement is available, the estimated error state set is updated according to

$$\begin{aligned} \varvec{\delta } \hat{\mathbf x}_k^+ = \varvec{\delta } \hat{\mathbf x}_k^- + {\mathbf K}_k({\varvec{\delta } {\mathbf y}_k-{\varvec{{h}}}_k(\hat{{\mathbf x}}_k^-+\varvec{\delta } \hat{\mathbf x}_k^-)+{\varvec{{h}}}_k(\hat{{\mathbf x}}_k^-)}) , \end{aligned}$$
(18)

where \(\varvec{\delta } {\mathbf y}\) is computed from the actual measurement \(\tilde{\mathbf y}\) as \(\varvec{\delta } {\mathbf y}= \tilde{\mathbf y}-\hat{\mathbf y}= \tilde{\mathbf y}- {\varvec{{h}}}(\hat{\mathbf x}_{k}^-)\). The superscripts ‘−’ and ‘\(+\)’ mean a priori (before the update) and a posteriori (after the update), respectively. The Kalman gain is here the same as in a regular EKF,

$$\begin{aligned} {\mathbf K}_k = {\mathbf P}_k^-{\mathbf H}_k^{{\mathsf {T}}}{\mathbf S}_k^{-1} , \end{aligned}$$
(19)

and so is the filter covariance propagation,

$$\begin{aligned} {\mathbf P}_k^+ = \left( {\mathbf {I}}- {\mathbf K}_k{\mathbf H}_k\right) {\mathbf P}_k^- . \end{aligned}$$
(20)

Following the update, the error states are feedforward to correct the whole state set (and strapdown integration routine), being the error state set then reset, i.e.

$$\begin{aligned} \hat{\mathbf x}_k^+&= \hat{\mathbf x}_k^- + \varvec{\delta } \hat{\mathbf x}_k^+\nonumber \\ \varvec{\delta } \hat{\mathbf x}_k^+&\leftarrow {\varvec{0}}. \end{aligned}$$
(21)

3.5 Filter state set and propagation model

The filter state set \({\mathbf x}\) can be split into three sub-sets: kinematics states \({\mathbf x}_\mathsf {kin}\), IMU model states \({\mathbf x}_\mathsf {imu}\), and CNav measurement model states \({\mathbf x}_\mathsf {cnav}\). The process model can then be written as:

$$\begin{aligned} \begin{bmatrix}{\mathbf x}_{\mathsf {kin},k+1}\\ {\mathbf x}_{\mathsf {imu},k+1}\\ {\mathbf x}_{\mathsf {cnav},k+1}\end{bmatrix} =\begin{bmatrix}{\varvec{\phi }} _{\mathsf {kin},k}({{\mathbf x}_{\mathsf {kin},k},{\mathbf u}_{k+1}(\tilde{\mathbf u}_{k+1},{\mathbf x}_{\mathsf {imu},k})})\\ {\varvec{\phi }} _{\mathsf {imu},k}({{\mathbf x}_{\mathsf {imu},k}})\\ {\varvec{\phi }} _{\mathsf {cnav},k}({{\mathbf x}_{\mathsf {cnav},k)}}\end{bmatrix}+ \begin{bmatrix}{\mathbf w}_{\mathsf {kin},k}\\ {\mathbf w}_{\mathsf {imu},k}\\ {\mathbf w}_{\mathsf {cnav},k}\end{bmatrix} , \end{aligned}$$
(22)

where \({\mathbf w}\) are process noise terms and \({\mathbf u}\) is the vector of corrected inertial increments,

$$\begin{aligned} {\mathbf u}_{k+1}({\tilde{\mathbf u}_{k+1}, {\mathbf x}_{\mathsf {imu},k}}) = \begin{bmatrix}\varvec{\varDelta } {\mathbf v}_{k+1}^B\\ \varvec{\varDelta } \varvec{\theta } _{k+1}^B\end{bmatrix} . \end{aligned}$$
(23)

\({\mathbf u}\) is a function of the actual (corrupted) measurements \(\tilde{\mathbf u}\) and the IMU error states \({\mathbf x}_\mathsf {imu}\). This relation will be further discussed in Sect. 3.5.1.

The kinematics state portion \({\mathbf x}_\mathsf {kin}\) includes position \({\mathbf r}^M\), velocity \({\mathbf v}^M\) and attitude quaternion \({\mathbf q}_B^M\). To these states, a set of error states is assigned as:

$$\begin{aligned} \varvec{\delta } {\mathbf x}_\mathsf {kin}= \begin{bmatrix}\varvec{\delta } {\mathbf v}^M\\ \varvec{\delta } {\mathbf r}^M\\ \varvec{\delta } \varvec{\theta } ^B\end{bmatrix} . \end{aligned}$$
(24)

Note that the attitude error angle \(\varvec{\delta } \varvec{\theta } ^B\) is defined not as an additive error term (as the other error states) but as

$$\begin{aligned} \begin{bmatrix}\frac{1}{2}\varvec{\delta } \varvec{\theta } _k^B\\ 1\end{bmatrix}\approx {\mathbf q}^{M_k}_{B_k}\left( \hat{\mathbf q}^{M_k}_{B_k}\right) ^{-1}. \end{aligned}$$
(25)

The kinematics error state propagation model is derived through the linearization of (3), (4) and (1) yielding

$$\begin{aligned} \varvec{\delta } {\mathbf v}_{k+1}^M&\approx {\mathbf C}_{M_k}^{M_{k+2}}\varvec{\delta } {\mathbf v}_k^M -\Delta t_k{\varvec{\varOmega } _{IM}^M}^2{\mathbf C}_{M_k}^{M_{k+1}}\varvec{\delta } {\mathbf r}_k^M \nonumber \\&\quad +\left( {\mathbf {I}}-\frac{\Delta t_k}{2}\varvec{\varOmega } _{IM}^M\right) {\mathbf C}_{I}^{M_{k+1}}({\varvec{\delta } \varvec{\varDelta } {\mathbf v}^I_{\mathsf {sf},k+1}+\varvec{\delta } \varvec{\varDelta } {\mathbf v}^I_{\mathsf {g},k+1}}) \nonumber \\&\quad + {\mathbf w}_{{\mathrm{v}},k},\end{aligned}$$
(26)
$$\begin{aligned} \varvec{\delta } {\mathbf r}_{k+1}^M&\approx \Delta t_k{\mathbf C}_{M_k}^{M_{k+1}}\varvec{\delta } {\mathbf v}_k^M + \varvec{\delta } {\mathbf r}_k^M \nonumber \\&\quad +\frac{\Delta t_k}{2}{\mathbf C}_{I}^{M_{k+1}}({\varvec{\delta } \varvec{\varDelta } {\mathbf v}^I_{\mathsf {sf},k+1}+\varvec{\delta } \varvec{\varDelta } {\mathbf v}^I_{\mathsf {g},k+1}}) + {\mathbf w}_{\mathrm{r},k} ,\end{aligned}$$
(27)
$$\begin{aligned} \varvec{\delta } \varvec{\theta } _{k+1}^B&\approx \hat{\mathbf C}_{B_k}^{B_{k+1}}\varvec{\delta } \varvec{\theta } _k^B-\varvec{\delta } \varvec{\varDelta } \varvec{\theta } _{k+1}^B + {\mathbf w}_{\theta ,k} . \end{aligned}$$
(28)

with

$$\begin{aligned} \varvec{\delta } \varvec{\varDelta } {\mathbf v}^I_{\mathsf {g},k+1}&\approx \Delta t_k\;{\mathbf C}_{M_{k+\frac{1}{2}}}^{I} {\varvec{{G}}}\left( \hat{\mathbf r}^M_{k+\frac{1}{2}}\right) {\mathbf C}_{M_k}^{M_{k+\frac{1}{2}}}\left( \varvec{\delta } {\mathbf r}_k^M+\frac{\Delta t_k}{2}\varvec{\delta } {\mathbf v}_k^M\right) \end{aligned}$$
(29)
$$\begin{aligned} \varvec{\delta } \varvec{\varDelta } {\mathbf v}^I_{\mathsf {sf},k+1}&\approx {\mathbf C}_{M_k}^{I}\hat{\mathbf C}_{B_k}^{M_k}\left( \bigl [\hat{\mathbf C}_{B_{k+\frac{1}{2}}}^{B_k}\varvec{\varDelta } \hat{\mathbf v}_{k+1}^B \times \bigr ]\varvec{\delta } \varvec{\theta } _k^B \right. \nonumber \\&\quad \left. +\hat{\mathbf C}_{B_{k+\frac{1}{2}}}^{B_k}\varvec{\delta } \varvec{\varDelta } {\mathbf v}_{k+1}^B -\frac{1}{2}\bigl [\varvec{\varDelta } \hat{\mathbf v}_{k+1}^B \times \bigr ]\varvec{\delta } \varvec{\varDelta } \varvec{\theta } ^B_{k+1}\right) , \end{aligned}$$
(30)

where the gravity gradient \({\varvec{{G}}}({\mathbf r})\) is given by

$$\begin{aligned} {\varvec{{G}}}({\mathbf r}) = \frac{{\partial }{\varvec{{g}}}({\mathbf r})}{{\partial }{\mathbf r}} \approx -\frac{\mu }{\Vert {\mathbf r}\Vert ^3}\left( {\mathbf {I}}- 3\frac{{\mathbf r}{\mathbf r}^{{\mathsf {T}}}}{\Vert {\mathbf r}\Vert ^2}\right) , \end{aligned}$$
(31)

being \(\mu\) the planet’s gravitational parameter.

The inertial increment errors \(\varvec{\delta } \varvec{\varDelta } {\mathbf v}^B\) and \(\varvec{\delta } \varvec{\varDelta } \varvec{\theta } ^B\) depend on the IMU error states and correction models used. This is covered in the following point.

3.5.1 IMU error model

The inertial increment set \({\mathbf u}\) in (22) is obtained from the correction of the actual inertial sensor measurements \(\tilde{\mathbf u}\). In this study, we define the inertial measurement correction model (23) as

$$\begin{aligned} \varvec{\varDelta } {\mathbf v}^B_{k+1}&= ({{\mathbf {I}}-{{\mathrm{diag}}}({\mathbf s}_{\mathsf {a},k}^B)-[{\varvec{\vartheta } _{\mathsf {a},k}^B} X] - {\mathbf S}(\varvec{\eta } _{\mathsf {a},k}^B)})\varvec{\varDelta } \tilde{{\mathbf v}}_{k+1}^B \nonumber \\&\quad -\Delta t_{k+1}{\mathbf b}_{\mathsf {a},k}^B+\varvec{\nu } _{\mathsf {a},k}^B, \end{aligned}$$
(32)
$$\begin{aligned} \varvec{\varDelta } \varvec{\theta } ^B_{k+1}&= ({{\mathbf {I}}-{{\mathrm{diag}}}({\mathbf s}_{\mathsf {g},k}^B)-[{\varvec{\vartheta } _{\mathsf {g},k}^B} X ]- {\mathbf S}(\varvec{\eta } _{\mathsf {g},k}^B)}\varvec{\varDelta } \tilde{\varvec{\theta }}_{k+1}^B) \nonumber \\&\quad - \Delta t_{k+1}\, {\mathbf b}_{\mathsf {g},k}^B+\varvec{\nu } _{\mathsf {g},k}^B , \end{aligned}$$
(33)

where \({\mathbf S}(\cdot )\) is a symmetric matrix defined as:

$$\begin{aligned} {\mathbf S}(\varvec{\eta }) = \begin{bmatrix}0&\eta _3&\eta _2\\\eta _3&0&\eta _1\\\eta _2&\eta _1&0\end{bmatrix} . \end{aligned}$$
(34)

The IMU parameters \({\mathbf s}\), \(\varvec{\vartheta }\), \(\varvec{\eta }\), \({\mathbf b}\) and \({\varvec{ v }}\) in (32) and (33) are identified and described in Table 1.

Table 1 IMU states definition and stochastic modeling
Full size table

The error input vector

$$\begin{aligned} \varvec{\delta } {\mathbf u}_k&= {\mathbf u}_{k+1}({\tilde{\mathbf u}_{k+1}, {\mathbf x}_{\mathsf {imu},k}}) - \hat{\mathbf u}_{k+1}({\tilde{\mathbf u}_{k+1}, \hat{\mathbf x}_{\mathsf {imu},k}}) \nonumber \\&= \begin{bmatrix}\varvec{\delta } \varvec{\varDelta } {\mathbf v}^B_{k+1}\\ \varvec{\delta } \varvec{\varDelta } \varvec{\theta } ^B_{k+1}\end{bmatrix} \end{aligned}$$
(35)

has its components given through the linearization of (32) and (33) as:

$$\begin{aligned} \varvec{\delta } \varvec{\varDelta } {\mathbf v}^B_k&= -{{\mathrm{diag}}}({\varvec{\varDelta } \tilde{{\mathbf v}}_{k+1}^B})\varvec{\delta } {\mathbf s}_{\mathsf {a},k}^B+[{\varvec{\varDelta } \tilde{{\mathbf v}}_{k+1}^B} X ]\varvec{\delta } \varvec{\vartheta } _{\mathsf {a},k}^B \nonumber \\&\quad - {\mathbf S}({\varvec{\varDelta } \tilde{{\mathbf v}}_{k+1}^B})\varvec{\delta } \varvec{\eta } _{\mathsf {a},k}^B -\Delta t_{k+1}\varvec{\delta } {\mathbf b}_{\mathsf {a},k}^B + \varvec{\nu } _{\mathsf {a},k},\end{aligned}$$
(36)
$$\begin{aligned} \varvec{\delta } \varvec{\varDelta } \varvec{\theta } ^B_k&= -{{\mathrm{diag}}}({\varvec{\varDelta } \tilde{\varvec{\theta }}_{k+1}^B})\varvec{\delta } {\mathbf s}_{\mathsf {g},k}^B +[{\varvec{\varDelta } \tilde{\varvec{\theta }}_{k+1}^B} X ]\varvec{\delta } \varvec{\vartheta } _{\mathsf {g},k}^B \nonumber \\&\quad - {\mathbf S}({\varvec{\varDelta } \tilde{\varvec{\theta }}_{k+1}^B})\varvec{\delta } \varvec{\eta } _{\mathsf {g},k}^B - \Delta t_{k+1}\varvec{\delta } {\mathbf b}_{\mathsf {g},k}^G+\varvec{\nu } _{\mathsf {g},k} , \end{aligned}$$
(37)

where \(\varvec{\delta } {\mathbf s}\), \(\varvec{\delta } \varvec{\vartheta }\), \(\varvec{\delta } \varvec{\eta }\) and \(\varvec{\delta } {\mathbf b}\) are the error states corresponding to the IMU states in (32) and (33).

The construction of the process function \({\varvec{\phi }} _{\mathsf {imu}}(\,\cdot \,)\) is straightforward from the processes in Table 1.

3.6 Measurement update models

The CNav outputs position and attitude information. The following points describe the filter update models for these two measurements. As previously mentioned, the filter updates are done whenever a measurement is available (cf. Sect. 4.1).

3.6.1 Position update

The position fixes handed out by the CNav are relative to the center of frame M and written in coordinates of this frame. The measurement is modeled as:

$$\begin{aligned} {\mathbf y}_{\mathrm{r},k} = \tilde{\mathbf r}_{\mathsf {cnav},k}^M&= {\varvec{{h}}}_{\mathrm{r},k}({\mathbf x}_{k})+\varvec{\nu } _{\mathrm{r},k} \nonumber \\&= {\mathbf r}_k^M + {\mathbf C}_{B_k}^{M_k}{\mathbf l}_{\mathsf {cam}}^B + {\mathbf b}_{\mathsf {cnav},\mathsf {r},k}^M + \varvec{\nu } _{\mathrm{r},k} , \end{aligned}$$
(38)

where \({\mathbf l}_{\mathsf {cam},k}^B\) is the arm between the center of the IMU and the camera’s focal point in B coordinates; \({\mathbf b}_{\mathsf {cnav},\mathsf {r},k}^M\) is the measurement position bias state; and \(\varvec{\nu } _{\mathrm{r},k}\sim \mathcal {N}({\varvec{0}},{\mathbf R}_{\mathrm{r},k})\) is measurement noise.

The error measurement model is derived as:

$$\begin{aligned} \varvec{\delta } {\mathbf y}_{\mathrm{r},k}&= {\varvec{{h}}}_{\mathrm{r},k}(\hat{\mathbf x}_{k}+\varvec{\delta } {\mathbf x}_{k}) - {\varvec{{h}}}_{\mathrm{r},k}(\hat{\mathbf x}_{k}) + \varvec{\nu } _{\mathrm{r},k} \nonumber \\&\approx \hat{{\mathbf r}}_k^M+\varvec{\delta } {{\mathbf r}}_k^M + \hat{\mathbf C}_{B_k}^{M_k}({{\mathbf {I}}-[{\varvec{\delta } \varvec{\theta } _k^B} }X ]){\mathbf l}_{\mathsf {cam}}^B + \hat{\mathbf b}_{\mathsf {cnav},\mathrm{r},k}^M \nonumber \\&\quad +\varvec{\delta } {\mathbf b}_{\mathsf {cnav},\mathrm{r},k}^M - \hat{{\mathbf r}}_k^M - \hat{\mathbf C}_{B_k}^{M_k}{\mathbf l}_{\mathsf {cam}}^B -\hat{\mathbf b}_{\mathsf {cnav},\mathrm{r},k}^M+\varvec{\nu } _{\mathrm{r},k}\nonumber \\&\approx \varvec{\delta } {{\mathbf r}}_k^M + \hat{\mathbf C}_{B_k}^{M_k}[{{\mathbf l}_{\mathsf {cam}}^B} X ]\varvec{\delta } \varvec{\theta } _k^B +\varvec{\delta } {\mathbf b}_{\mathsf {cnav},\mathrm{r},k}^M +\varvec{\nu } _{\mathrm{r},k} , \end{aligned}$$
(39)

where the second-order error terms have been neglected.

The measurement bias state \({\mathbf b}_{\mathsf {cnav}}^M\) is modeled as a random walk process with random initial condition given by \({\mathbf b}_{\mathsf {cnav},0}^M\sim \mathcal {N}({\varvec{0}},\varvec{\sigma } ^2_{\mathrm{b} _0,\mathsf {cnav}})\).

The measurement model Jacobian \({\mathbf H}_{\mathrm{r},k}\) is easily extracted from (39).

3.6.2 Attitude update

The CNav attitude output is expressed as a quaternion from C frame to M frame. The model for this measurement is

$$\begin{aligned} \tilde{{\mathbf q}}_{C_k}^{M_k} = {\mathbf q}({\varvec{\nu } _{\mathrm {q},k}}) {\mathbf q}_{C_k}^{B_k} {\mathbf q}({{\mathbf b}_{\mathrm {q},k}^B}) {\mathbf q}_{B_k}^{M_k} \end{aligned}$$
(40)

\({\mathbf b}_{\mathrm {q},k}^B\) is a three-axis attitude bias (in body frame) and \(\varvec{\nu } _{\mathrm {q},k}\sim \mathcal {N}({\varvec{0}},{\mathbf R}_{\mathrm {q},k})\) is measurement noise. The quaternion mappings \({\mathbf q}(\,\cdot \,)\) are given as

$$\begin{aligned} {\mathbf q}\left( {\mathbf v}\right) = \begin{bmatrix}\frac{1}{2}{\mathbf v}\\ \sqrt{1-\Vert \frac{1}{2}{\mathbf v}\Vert ^2}\end{bmatrix} , \end{aligned}$$
(41)

where \({\mathbf v}\) is a three-element small angle rotation.

The error measurement model is given through

$$\begin{aligned} \varvec{\delta } {\mathbf q}_k ({\varvec{\delta } {\mathbf y}_{\mathrm {q},k}})&= {\mathbf q}({\varvec{\nu } _{\mathrm {q},k}}) {\mathbf q}_{C_k}^{B_k} {\mathbf q}({{\mathbf b}_{\mathrm {q},k}^B}) {\mathbf q}_{B_k}^{M_k}({{\mathbf q}_{C_k}^{B_k}){\mathbf q}({\hat{\mathbf b}_{\mathrm {q},k}^B})\hat{\mathbf q}_{B_k}^{M_k}} ^{-1}\nonumber \\&= {\mathbf q}({\varvec{\nu } _{\mathrm {q},k}}) {\mathbf q}_{C_k}^{B_k} {\mathbf q}({{\mathbf b}_{\mathrm {q},k}^B}) {\mathbf q}({\varvec{\delta } \varvec{\theta } ^B_k}) \hat{\mathbf q}_{B_k}^{M_k}({\hat{\mathbf q}_{B_k}^{M_k}}) ^{-1}{\mathbf q}({-\hat{\mathbf b}_{\mathrm {q},k}^B}) {\mathbf q}_{B_k}^{C_k} \nonumber \\&= {\mathbf q}({\varvec{\nu } _{\mathrm {q},k}}) {\mathbf q}_{C_k}^{B_k} {\mathbf q}({{\mathbf b}_{\mathrm {q},k}^B}) {\mathbf q}({\varvec{\delta } \varvec{\theta } ^B_k}) {\mathbf q}({-\hat{\mathbf b}_{\mathrm {q},k}^B}) {\mathbf q}_{B_k}^{C_k} . \end{aligned}$$
(42)

Note that the transformation between camera frame C and body frame B is assumed perfectly known. Any misalignment in this rotation will effectively be captured by the measurement bias \({\mathbf b}_{\mathrm {q}}\).

Inverting the quaternion mapping \(\varvec{\delta } {\mathbf q}({\varvec{\delta } {\mathbf y}_{\mathrm {q}}})\) to obtain \(\varvec{\delta } {\mathbf y}_{\mathrm {q},k}\) yields

$$\begin{aligned} \varvec{\delta } {\mathbf y}_{\mathrm {q},k} = \varvec{\delta } \varvec{\theta } ^B_k + \varvec{\delta } {\mathbf b}_{\mathrm {q},k}^B +\varvec{\nu } _{\mathrm {q},k} , \end{aligned}$$
(43)

having the second-order error terms been neglected.

The attitude bias state \({\mathbf b}_{\mathrm {q},k}^B\) is modeled as a random walk plus an initial random constant to account for the mounting misalignments.

Again, the measurement model Jacobian \({\mathbf H}_{\mathrm {q},k}\) is easily extracted from (43).

3.7 Outlier detection and rejection

To render robustness of the integrated system against bad samples (outliers) from the CNav, a detection and rejection scheme was implemented.

The filter innovations, as implicitly defined in (18), are given by

$$\begin{aligned} {\mathbf z}_k = \varvec{\delta } {\mathbf y}_k - \varvec{\delta } \hat{\mathbf y}_k . \end{aligned}$$
(44)

The sum of squares of normalized versions of these innovations, defined as [4]

$$\begin{aligned} {T} _{{ z},k}^2 = {\mathbf z}_k^{{\mathsf {T}}}{\mathbf S}_k ^{-1}{\mathbf z}_k , \end{aligned}$$
(45)

should follow a \(\chi ^2\)-distribution with \(n_{ z}\)-degrees of freedom, where \(n_{ z}\) is the dimension of \({\mathbf z}\) (in this case 6). \(T^2_{z,k}\) is a powerful indicator of filter consistency, being commonly used to detect measurement/model faults and outliers.

The value of \({T} ^2_{{ z},k}\) is compared to a threshold and, if larger, rejected. A threshold value of 30 was used in this work.

4 Test setup

As the data evaluated in this paper are the outcome of a recent flight campaign, the experimental setup shall be introduced here. The overall test concept was to fly a navigation sensor suite along a predefined trajectory over a field of craters which had been mapped into an Earth fixed frame. During flight, data from the sensor suite and ground truth were acquired simultaneously.

The flight’s objective was to demonstrate the real-time closed-loop operation of an optically augmented navigation system in an exploration mission scenario. The navigation system is a product of the DLR developed ATON activity. The discussion of the successful results of this system will be part of a future publication. More information on previous tests of this platform can be found in [1].

4.1 Trajectory and flight apparatus

The test campaign took place near Braunschweig, Germany, at a test site offering a strip of land and volume of restricted airspace suitable for flying unmanned vehicles over an area of about 300 \(\times\) 300 m (Fig. 5a). The job of transporting the navigation payload was performed by an unmanned SwissDrones (SDO 50 V2) helicopter (Fig. 6a). This platform is capable of autonomous, assisted and remote-controlled flight and it offers a payload capability of approximately 50 kg (fuel plus experiment equipment).

Fig. 5
figure 5

Overview of test area and trajectory

Full size image

All sensors were integrated on one single platform. The devices relevant for this paper are marked in the image of the experimental payload in Fig. 6a. A tactical-grade IMU (iMAR iTraceRT-F400-Q-E, specifications in Table 2) was used for acquiring velocity and angle increments. It operated at 100 Hz. Capturing of images was performed by a monocular, monochromatic camera (Prosilica GT1380). Having been installed in a forward-looking configuration, its resolution was set to 1024 px \(\times\) 1024 px. The camera images served as input to two algorithms, a high-framerate feature tracker (measurements not used and method not covered by this paper) and the lower-framerate CNav algorithm. For supplying the high-framerate task, the camera was triggered at 20 Hz. The asynchronous crater navigation was always provided the most recent image at a rate ranging from 3 to 5 Hz, depending on the individual image processing load. A laser altimeter was installed adjacent to the camera, pointing in parallel with the camera boresight. Measurements from this sensor, although not included in the hybrid navigation setup here proposed (nor in the ground truth generation), shall be employed in Sect. 5.1 to analyze the noise profile of CNav.

Fig. 6
figure 6

Setup of payload hardware and craters

Full size image
Table 2 IMU (1\(\sigma\)) specifications
Full size table

Considering the experience of earlier activities with the CNav system, a position accuracy in the order of low one-digit percent of (camera) line-of-sight range was assumed as a likely upper bound, as the detection algorithm’s performance is slightly impacted when operating with the artificial crater targets instead of real craters. Given the flight trajectory followed (Fig. 5b), this translates to a ground truth accuracy requirement of centimeter level. Therefore, the helicopter payload was equipped with a high-grade GNSS receiver NovAtel Propak6. This uses both L1 and L2 frequencies and the German precise satellite positioning service, SAPOS. This service relies on a network of reference stations with precisely known positions that determines corrective data for all visible GPS satellites. Furthermore, two GNSS antennas were used allowing the receiver to also determine heading and pitch in the North East Down reference system. The Propak6 output has the following \(1\sigma\) accuracies: about 0.03 m in position, about 0.4\(^{\circ }\) in heading and pitch, and about 0.03 m/s in velocity.

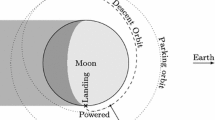
About half of the available terrain in Fig. 5a was used for the flight trajectory. The remainder was reserved as safety perimeter, ground station and test crew area. The reference flight trajectory was defined as a linear path, stretching from north-east to south-west for about 200 m, and from an initial altitude of 50 m down to 10 m. There, the helicopter performed a vertical descent down to 1 m above ground. Fig. 5b illustrates this profile.

Obviously, craters are necessary for the CNav unit to function. A pattern of planar crater targets (Fig. 6b) was thus scattered in a random manner over four sub-fields along the trajectory. Altogether, 80 craters with diameters between 5 m and 0.5 m were used. The bigger craters were situated near the beginning of the path (higher altitudes) and the smaller craters nearer to the end (lower altitudes), ensuring a near-constant coverage of the camera images during the linearly decreasing altitude. After placing the crater planes, these were fixed to the ground by amassing soil along their circumference (Fig. 6b). A picture of the crater scattering is shown in Fig. 7.

Fig. 7
figure 7

Helicopter over crater field during flight test

Full size image

4.2 Crater catalog

Subsequent to field preparation, a catalog of crater positions was created. The pose estimated by the CNav unit is relative to this reference database. Tasks such as autonomous navigation for lunar landing or near-asteroid operation require the crater navigation to provide a pose in the reference frame of the target body. Therefore, the crater catalog was in this case expressed in the Earth-Centered Earth-Fixed (ECEF) reference system. A two-stage process was performed: At first, a tachymeter (Leica TDRA6000) was used to measure all crater centers and three auxiliary points in a local (tachymeter) frame. Then, using the Propak6, the same three auxiliary points were measured directly in ECEF. This allowed the determination of a transformation from the local tachymeter reference frame into ECEF. Applying this transformation to all measured craters yielded the ECEF crater catalog. The accuracy of this catalog is then at the level of 0.01–0.02 m.

This level of accuracy is currently not achievable for lunar landings, where the best publicly available map material is derived from images of the lunar reconnaissance orbiter (LRO) narrow angle camera (NAC). This material delivers resolutions of up to 30 cm per map pixel, limiting the accuracy of crater maps and the resulting position measurement accuracy to this order of magnitude. However, this becomes relevant only below altitudes at which a lander would have switched to hazard avoidance mode and ceased relying on the CNav terrain-relative measurements for guidance. At higher altitudes, the CNav measurement accuracy is limited by the camera resolution and not by the map resolution.

4.3 Ground truth

As mentioned above, a high-end GNSS receiver was used as means to obtain a ground truth for the tested trajectories. In an effort to increase the accuracy of this information, the output of the Propak6 receiver was fused with IMU data in post-processing. This not only smoothed the position and velocity solutions but also completed the 2 DoF attitude information given by the receiver (pitch and heading). The slight observability of attitude provided by the accelerometer measurements in combination with measured position and velocity further increased overall attitude accuracy. The covariance levels of kinematics states of the fused ground truth can be seen in Fig. 8.

Fig. 8
figure 8

Fused ground truth quality (\(1\sigma\) covariance)

Full size image

5 Test results

In this section, we first analyze the characteristics of the raw CNav system output, and then its fusion with inertial data from the IMU.

5.1 CNav output performance

The Crater Navigation unit (CNav), described in Sect. 2, delivers ECEF position and camera frame (C) to ECEF attitude solutions at a rate up to 5 Hz.

Figure 9 shows the error (w.r.t. the ground truth) of the CNav position output in both ECEF and camera frames. In both reference frame representations of this error, a decreasing variance can be observed. This is to be explained by the increased effective resolution of the camera as the target surface is closing in during the flight. This almost linear decrease in error variance over time correlates with the direct line-of-sight range measurement (denoted LoS) of the laser altimeter aligned in parallel with the navigation camera’s optical axis as shown in Fig. 10.

Fig. 9
figure 9

Error in CNav position in-flight solutions

Full size image
Fig. 10
figure 10

Line-of-sight range measured by altimeter pointing along the camera’s optical axis

Full size image

Normalizing the CNav position errors with the altimeter line-of-sight range removes the visible time dependence in Fig. 9. The result is shown in Fig. 11a expressed in camera frame C. We base the position measurement model on this normalization strategy. Figure 11b presents the distribution of these normalized errors. These distributions appear nearly Gaussian and, therefore, suitable to be used in an EKF design. There are, however, outliers visible that do not appear to be consistent with the Gaussian hypothesis. This motivates our design decision to include an outlier rejection mechanism based on the gating of normalized innovations. In the camera reference frame, the error distribution displays a clear bias in the direction of the camera optical axis, with the empirical distribution being “smeared” from its shifted mode towards zero. Hence, we suspect that this is the result of mis-calibration that yielded a sub-optimal focal length value.

Fig. 11
figure 11

Normalization of CNav position errors

Full size image

The CNav raw output attitude error relative to the ground truth is display in Fig. 12a expressed in body frame and in Fig. 12b in camera frame. These measurement errors show largely constant variance over the duration of the flight experiment. This is to be expected, as the attitude measurement as an angular quantity cannot improve with decreasing line of sight. Figure 12c shows that the distributions of the attitude errors (in C frame) again resemble a Gaussian. As in the case of position measurements, outliers are evident, once more justifying the use of a detection and rejection scheme. There are again biases in these error distributions, here in the order of one degree. After comparing data from multiple flights in which these biases were constant, we attribute them to camera-to-IMU residual misalignment and not to the CNav algorithm.

Fig. 12
figure 12

Error in CNav attitude in-flight solutions

Full size image

As we suspected that the method of simultaneous recovery of the camera position and attitude from the PnP problem of matched image and world reference points should not yield six independent degrees of freedom, we investigated the raw errors with regard to cross-correlations between components of position and attitude.

Our suspicion is confirmed by the upper right and lower left 3 \(\times\) 3 blocks of the raw measurement error covariance matrix

$$\begin{aligned} {\mathbf R}&= \mathrm{E} \left\{ \begin{bmatrix}\frac{1}{\mathsf {LoS}}\left( \varvec{\delta } {\mathbf r}_{\mathsf {cnav}}^E\right) \\ \varvec{\delta } \varvec{\theta } ^B_{\mathsf {cnav}}\end{bmatrix} \begin{bmatrix}\frac{1}{\mathsf {LoS}}\left( \varvec{\delta } {\mathbf r}_{\mathsf {cnav}}^E\right) \\ \varvec{\delta } \varvec{\theta } ^B_{\mathsf {cnav}}\end{bmatrix}^{{\mathsf {T}}}\right\} \nonumber \\ =&10^{-3}\begin{bmatrix}0.4008&0.1785&0.1366&0.1922&0.3365&-0.0510\\ 0.1785&0.3535&-0.0768&0.3086&0.0939&-0.1557\\ 0.1366&-0.0768&0.4150&-0.1415&0.2168&0.0799\\ 0.1922&0.3086&-0.1415&0.3753&0.0953&-0.1182\\ 0.3365&0.0939&0.2168&0.0953&0.3245&-0.0078\\ -0.0510&-0.1557&0.0799&-0.1182&-0.0078&0.1161\end{bmatrix} \end{aligned}$$
(46)

that display clearly a strong coupling of position and attitude. In (46), the quantity \(\mathsf {LoS}\) is the line-of-sight range, and \(\varvec{\delta } {\mathbf r}_{\mathsf {cnav}}^E\) and \(\varvec{\delta } \varvec{\theta } ^B_{\mathsf {cnav}}\) are, respectively, the CNav position error (in meters) and the attitude error (as a small angle rotation, in rad). Neglecting the couplings by assuming independence of measurements would lead to a suboptimal filter design. For this reason, we include them in our measurement model. The position and attitude measurement update is then done using the noise covariance matrix (46).

5.2 Hybrid navigation results

We now present the results of the filtering proposed for the fusion of CNav solutions and inertial data.

Figure 13 shows position, velocity and attitude errors of the fused solutions, again w.r.t. the flight ground truth. Coherent filter behaviour is attested by the \(1\sigma\) bounds displayed, which include uncertainty contributions from the ground truth signals (Fig. 8). The filter is initialized with the first CNav fix available (\(t=0\) s) which is assumed to follow the distributions in Figs. 11b and 12c.

A direct comparison of the filtered results with the raw CNav output samples, in Fig. 14, clearly reveals the advantage of the fusion setup. Note that, because of the slight attitude observability granted by the body acceleration measurements (accelerometer) in combination with ECEF position ones (CNav), the pitch and roll accuracy (x and y axes) converge more quickly than to be expected from the biased raw CNav solutions alone. Attitude around yaw axis (z) is mostly observable through CNav attitude fixes, thus showing a slower convergence.

Fig. 13
figure 13

Fused CNav and IMU performance in terms of position, velocity and attitude errors with \(1\sigma\) covariance as faded colored lines

Full size image

In case of temporary unavailability of the CNav solution, inertial measurements ensure navigation continuity. As shown in Fig. 15, the filter solution visibly diverges during simulated CNav absence from 100 to 200 s. Velocity and position see a much stronger effect than attitude. This is explained by the benign rotational motion of the vehicle in combination with the relatively low bias of the employed gyro (Table 2).

Fig. 14
figure 14

Comparison of raw (CNav) and fused (CNav + IMU) position and attitude errors

Full size image
Fig. 15
figure 15

Position, velocity and attitude performance of the fused solution under CNav fix interruption from 150 to 200 s. \(1\sigma\) covariance as faded colored lines

Full size image

The capability of the CNav measurements to calibrate the Tactical-grade IMU errors online can be assessed by looking at the covariance bounds of the IMU states within the fusion filter. These are shown in Fig. 16. Accelerometer bias seems to be the most observable quantity (especially the z-axis, given that the levelled flight is mostly aligned with the vertical). Accelerometer scale factor in this direction is also reasonably calibrated, as are the x and y directions of the gyroscope bias. The remaining quantities (and axes) are either very slightly observable or non-observable altogether in this setup and trajectory. This insight is crucial if the fusion algorithm is to have its order reduced through the use of consider states, i.e., states which are not explicitly estimated but whose uncertainty is taken into account in filter operation (covariance propagation and filter update) [15]. States with low or null observability are good candidates for consider states. This method leads to some degree of complexity reduction in the real-time implementation.

Fig. 16
figure 16

Filter covariance (\(1\sigma\)) of IMU model states in body frame: x-axis (red line), y-axis (green line), and z-axis (blue line)

Full size image

Finally, we analyze the filter innovations. Figure 17a shows the sum of squares of normalized innovations, \(T^2_z\), as described in Sect. 3.7. The rejection threshold (set to 30) and detected outliers are also shown. The distribution of \(T^2_z\) is displayed in Fig. 17b. Note how it resembles much more a \(\chi ^2\) distribution of 3 DoF rather than the 6 DoF, which is the dimension of the full measurement. We consider this confirmation of our suspicion that the loose coupling of the IMU with EPnP-based attitude and position data pairs would yield internally correlated measurements, as elaborated at the end of Sect. 2.

Fig. 17
figure 17

Sum of squares of normalized innovations, \(T^2_z\), value and distribution

Full size image

6 Conclusion

In the context of a helicopter drone flight experiment, we discussed the problem of integrating low-frequency position and attitude measurements from a crater detection and matching algorithm in a loosely-coupled extended Kalman filter setup with high-frequency IMU data.

A sufficiently accurate time-varying position measurement model could be designed with the aid of knowledge about the camera’s line-of-sight to the observed terrain. By analyzing raw crater-based and combined position and attitude measurement errors w.r.t. ground truth, we modeled cross-couplings between position and attitude measurements to enable coherent fusion in a Kalman filter. Performance of the resulting filter confirmed a hypothesis of ours about the internal correlation of the measurements based on the structure of the EPnP/QCP algorithm that derives the camera pose from the crater detections and the crater database.

The solutions yielded by the filter were coherent and significantly improved w.r.t. to the raw CNav measurements. An outlier rejection scheme made sure erroneous CNav samples were detected and discarded, promoting filter smoothness and consistency. IMU state error covariance analysis revealed room for filter order reduction as several states were shown unobservable. Analysis of normalized innovation statistics showed the expected effective three degrees of freedom in the combined position–attitude update of the CNav.

While the navigation accuracy shown is certainly satisfactory with regards to the reference pinpoint landing scenario, we plan to improve on the fusion model in the future by implementing a tight coupling of the CNav crater detector to the IMU. This can be accomplished using the detected craters as separate bearing measurements instead of the EPnP/QCP least-squares full pose measurement. This complicates the filter design slightly, but is an opportunity to reject singular detection errors instead of using the uniformly degraded full pose as measurement.