1 Introduction

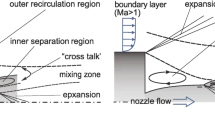
The wake of a classical space launcher at transonic speed is characterized by the shedding of the turbulent shear layer from the main body and its subsequent reattachment onto the thrust nozzle. Due to the highly unstable behavior of the shed shear layer and the recirculation region, wall pressure fluctuations and dynamic loads act on the structure of the nozzle which can lead to structural damage. The turbulent wake flow exhibits many similarities with the separated shear flow behind a backward-facing step (BFS). The flow over a BFS has been extensively studied experimentally, e.g., by Bradshaw and Wong [2], Eaton and Johnston [7], Simpson [26], and Driver et al. [6], and numerically, e.g., by Le et al. [14], Silveira Neto et al. [25], Friedrich and Arnal [9], and Kaltenbach and Janke [13]. A common observation of those investigations is an oscillating motion of the recirculation region and consequently the variation of the impingement location of the separated shear layer by about two step heights around the mean reattachment position. This so-called “flapping” of the shear layer is accompanied by pressure fluctuations at the lower wall at a Strouhal number of \(Sr_h=0.06{-}0.08\) based on the step height and the freestream velocity causing dynamic loads which are responsible for undesired structural vibrations called buffeting. The investigations on BFS flows are solely based on spanwise averaged flow properties. More recently, Statnikov et al. [27] and Scharnowski et al. [20] analyzed the three-dimensional wake of a generic planar model of a launcher and showed that the reattachment position varies over time not only in the streamwise but also in the spanwise direction. Using a DMD analysis, this variation in the reattachment process can be traced back to a coherent longitudinal cross-pumping motion of the recirculation bubble at \(Sr_h=0.01\) and a cross-flapping motion of the shear layer at \(Sr_h=0.07\).

Besides the investigations on planar configurations, a lot of research has been done on axisymmetric space launchers at transonic speed [4, 5, 15, 23, 28]. Schrijer et al. [23] detected by proper orthogonal decomposition (POD) two dominant wake modes containing the majority of the turbulent kinetic energy. The first mode captures a growing and shrinking of the separation zone most probably being the counterpart of the cross-pumping motion detected by Statnikov et al. [27] in the planar configuration. The second mode describes an undulating motion of the shear layer, thus, coinciding with the cross-flapping motion of the planar space launcher [27]. Deprés et al. [5] and Deck and Thorigny [4] performed a two-point correlation analysis in the wake of an axisymmetric configuration and detected an anti-phase oscillation with \(Sr_D\approx 0.2\) in the instantaneous wall pressure signal located at opposite sides in the azimuthal direction. They related this low-frequency oscillation to an antisymmetric mode leading to undesired side loads. For the development of efficient lightweight space launchers, it is essential to decrease the low-frequency dynamic loads arising due to such large-scale coherent motions. One promising possibility to manipulate the flow field and to reduce these loads is passive flow control. First applications of passive flow control in conjunction with space launchers can be traced back to the second half of the last century. Modified main bodies such as boat tails were extensively investigated [24] to increase the base pressure and thereby to reduce the overall drag. However, the purpose of the majority of the control devices examined in the recent past is a reduction of the reattachment length and thus the momentum arm to decrease the dynamic bending moments. It has been demonstrated that streamwise vortices intensify the turbulent mixing in the shear layer just downstream of the BFS leading to an increasing entrainment and spreading of the shear layer and consequently to a reduced reattachment length [11, 16]. Using tabs [16], chevrons [22], and castellation-like geometries [10], the reattachment length was reduced by up to 50%. The most promising approach to decrease the reattachment length is the so-called lobed mixer initially developed to reduce the noise in jet engines [30] but more recently also applied to a BFS configuration [1]. Due to the interaction of the spanwise and streamwise vortices generated by the lobes, the flow behind the lobed mixer becomes fully three-dimensional leading to an accelerated reattachment [26].

Fig. 1
figure 1

Passive flow control configurations. Boat tail (a) and semi-circular lobes (b)

Full size image

In this study, the effect of two passive flow control methods on the wake of a generic planar model of a space launcher is investigated. In the first approach, a standard boat tail is used. In the second configuration, a wavy trailing edge similar to that used by Bolgar et al. [1] is investigated. However, in the present analysis, only downward directed semi-circular lobes are used to avoid the substantial drag penalty caused by the upward directed lobes. Besides the reduction of the reattachment length, the lobes are to impair the large-scale coherent motion detected in the planar configuration without flow control by Statnikov et al. [27]. Sketches of the boat tail and the wavy trailing edge configurations are given in Fig. 1. For the investigations, a planar configuration is considered to enable a direct comparison with the configuration without flow control. Therefore, the conclusions cannot be directly transferred to an axisymmetric BFS configuration, since characteristic frequencies and spatial wave lengths may differ. However, the aforementioned work by Schrijer et al. [23] on an axisymmetric and by Statnikov et al. [27] on a planar configuration shows that there are some similarities between these two configurations.

Fig. 2
figure 2

Geometry parameters of the investigated generic planar transonic configuration [27]

Full size image

Besides classical statistical analysis such as mean and root-mean-square distributions and spectral analyses, i.e., Fourier transform, dynamic mode decomposition (DMD) is used to analyze the wake flow. The turbulent wake of the investigated generic space launchers is characterized by a superposition of a large number of coherent structures exhibiting various time and length scales. Therefore, the conjunction of detected distinct frequencies with the underlying physical flow mechanisms by classical statistical analysis is a challenging task. However, DMD, which belongs to a class of data-driven modal decomposition techniques, allows to isolate spatial modes of constant frequency from the complex wake flow, such that insight into the underlying wake flow phenomena is obtained. For instance, Statnikov et al. [27, 29] successfully applied DMD to time-resolved numerical data of transonic and supersonic wake flows of generic space launchers to determine coherent multi-dimensional flow patterns. In this study, DMD is used to understand the underlying flow phenomena leading to the periodic behavior of the wake flow determined by classical spectral analysis.

The paper is organized as follows. In Sect. 2, the respective geometries and the flow parameters are presented. The zonal RANS/LES method, the computational grids, and the DMD algorithm are briefly described. In Sect. 3, the results of the performed analysis are presented. Finally, conclusions are drawn and an outlook is given in Sect. 4.

2 Computational approach

2.1 Geometry and flow conditions

The influence of the passive flow control devices on the transonic wake flow is investigated on a planar generic space launcher configuration. The setup is based on the geometry of previous studies without flow control. It was defined in the framework of the German Collaborative Research Center Transregio 40 [27]. The launcher model is composed of a long shock-free forebody to avoid undesired shock–boundary interaction upstream of the investigated wake flow area and a backward-facing step. A sketch is given in Fig. 2. The main body diameter D and the step height \(h=0.3D\) of the BFS are chosen as reference values. In the corresponding experiments of the uninfluenced configuration, the model’s thickness D is 25 mm. The origin of the frame of reference is located in the lower corner of the BFS. The x-axis defines the streamwise direction and the y-axis the wall-normal direction. The forebody consists of a nose with a length of \(6\, D\) and a \(4\, D\) long main body with a thickness of D. A stick with a length of \(10\, D\) and a thickness of \(0.4\, D\) is mounted downstream of the main body. For the first configuration, the base shoulder of the main body is tapered by an angle of \(18^\circ\) to obtain a classical boat tail. The second passive flow control device consists of three equidistantly distributed semi-circular lobes integrated at the trailing edge of the main body. The diameter of the lobes as well as the distance between two adjacent lobes are \(0.8 \,h\) leading to a spanwise extension of the model of \(4.8\, h\). The lobe deflection angle is \(18^\circ\), thus exhibiting the same angle like the taper of the boat tail configuration. The selection of the geometry parameters is based on the parameter study of Bolgar et al. [1] who investigated the effect of different lobe radii varying from \(0.2 \,h\) to \(0.4 \,h\). The results reveal that lobes with a radius of 0.4 step heights, i.e., they have a size on the order of the thickness of the incoming boundary layer, show the largest impact on the wake topology. Therefore, the same radius is selected for this study. The simulations are performed at a freestream Mach number of \(Ma_\infty =0.8\) and a Reynolds number based on the height of the BFS of \(Re_{h}=1.8 \times 10^5\). The results are based on a sequence of 2048 time steps equidistantly sampled with \(t = 0.1D/u_\infty\). This leads to an overall time interval of \(204.8\, t_{\mathrm{ref}}\), with \(t_{\mathrm{ref}}=D/u_\infty\) being the reference time unit which is defined as the time a particle moving at freestream velocity \(u_\infty\) needs to cover the length of the main body’s thickness D. The CFL number is two and the time step is \(\Delta t=0.00005 t_{\mathrm{ref}}\) leading to 4.1 million iteration steps per simulation. In total, 6.2 million core hours distributed over 9600 cores have been used per simulation

2.2 Zonal RANS/LES flow solver

The time-resolved numerical computations are performed using a zonal RANS–LES finite-volume method. The computational domain is split into two parts, see Fig. 2. In the upstream domain which encloses the forebody, the RANS equations are solved. The flow around the boat tail or lobes and the wake are determined by an LES. The Navier–Stokes equations of a three-dimensional unsteady compressible fluid are discretized second-order accurate by a mixed centered/upwind advective upstream splitting method (AUSM) scheme for the Euler terms. The non-Euler terms are approximated second-order accurate using a centered scheme. For the temporal integration, an explicit 5-stage Runge–Kutta method of second-order accuracy is used. The monotone integrated LES (MILES) method determines the impact of the sub-grid scales. The solution of the RANS equations is based on the same discretization schemes. To close the time-averaged equations, the one-equation turbulence model of Fares and Schröder [8] is used. For a comprehensive description of the flow solver, see Statnikov et al. [27, 29].

Fig. 3
figure 3

Computational Grid for the LES zone. Boat tail configuration (right) which agrees with the computational grid in the streamwise symmetry plane of the lobes. Configuration with lobes (bottom). Every 12th grid point is shown

Full size image

The transition from the RANS to the LES domain is determined by the reformulated synthetic turbulence generation (RSTG) method developed by Roidl et al. [18, 19]. Turbulence is described as a superposition of coherent structures. The structures are generated at the inlet plane by superimposed virtual eddy cores. These eddy cores are defined at random positions \(\varvec{x}_i\) in a virtual volume \(V_{\mathrm{virt}}\) which encloses the inlet plane and exhibits the dimension of the turbulent length scale \(l_x\), the boundary-layer thickness at the inlet \(\delta _0\), and the width of the computational domain \(L_z\) in the streamwise, the wall-normal, and the spanwise direction. To take the inhomogeneity of the turbulent scales in the wall-normal direction into account, the virtual eddy cores are described by different shape factors and length and time scales depending on the wall-normal distance. Having N synthetic eddies, the normalized stochastic velocity fluctuations \(u'_m\) at the LES inlet plane are determined by the sum of the contribution \(u_m^i(\varvec{x},t)\) of each eddy core i:

$$\begin{aligned} u'_m\left( \varvec{x},t\right) =\frac{1}{\sqrt{N}}\sum _{i=1}^N \underbrace{\epsilon _i \, f_{\sigma ,m}^i \left( \varvec{x}-\varvec{x}_i\right) \,}_{u_m^i\left( \varvec{x},t\right) } \, \end{aligned}$$
(1)

with \(\epsilon _i\) being a random number within the interval \([-1,\,1]\), \(f_{\sigma ,m}^i\) being the shape function of the respective eddy, and \(m=1,2,3\) denoting the Cartesian coordinates in the streamwise, the wall-normal, and the spanwise direction. The final velocity components at the LES inflow plane \(u_m\) are composed of an averaged velocity component \(u_{\mathrm{RANS},m}\) from the RANS solution and the normalized velocity fluctuations \(u'_m\) which are subjected to a Cholesky decomposition \(A_{mn}\) to assign the values of the target Reynolds-stress tensor \(R_{mn}=A_{mn}^T\,A_{mn}\) corresponding to the turbulent eddy viscosity of the upstream RANS:

$$\begin{aligned} u_m\left( \varvec{x},t\right) =u_{\mathrm{RANS},m}+A_{mn} \, u'_m\left( \varvec{x},t\right) . \end{aligned}$$
(2)

A more detailed description of the zonal RANS/LES method specifying the shape functions and length scales is given in Refs. [18, 19].

2.3 Computational mesh

The computational domain is divided into a RANS part around the forebody where the flow is attached and an LES part enclosing the boat tail or lobes and the wake. To ensure comparability between the various configurations, the same RANS grid for the forebody is used. To reduce the computational costs, the simulation is only performed for the upper part of the flow field. The RANS domain extends to approximately 10D in the wall-normal direction and ends just upstream of the trailing edge of the main body. For a more detailed description of the RANS grid, the reader is referred to Statnikov et al. [27].

The LES section extends in the streamwise direction from \(x/D=-\,1\) to \(x/D=10\) and in the wall-normal direction from \(y/D=0\) to \(y/D=10.3\). The edge of the boat tail and the lobes is located at \(x/D=-\,0.37\). To ensure the recovery of a fully developed boundary layer, a transition length of more than three boundary layer thicknesses is requested within the RSTG approach. Since the boundary-layer thickness directly upstream of the flow control devices is \(\delta =0.15D\), the LES inflow plane is positioned at \(x/D=-\,1\) to guarantee a full recovery of the turbulent boundary layer upstream of the boat tail or lobes. The mean grid resolution in wall units \(l^+=\nu /u_\tau\) in the area of the LES inflow plane and around the flow control devices is \(\Delta x_{\mathrm{wall}}/l^+=30\), \({\Delta y_{\mathrm{wall}}/l^+=2}\), and \(\Delta z_{\mathrm{wall}}/l^+=20\) which results in a total number of about 197 million grid points for the boat tail configuration and 330 million grid points for the lobe case. In Fig. 3, the LES grid around the boat tail and the lobes as well as in the wake are shown.

2.4 Dynamic mode decomposition

The dynamic mode decomposition (DMD) is a data-driven modal decomposition technique based on the Koopman operator to determine a basis of non-orthogonal spatial modes each associated with a specific constant frequency from a multi-dimensional data field obtained from time-resolved experiments or numerical simulations. The extracted modes can be used to identify coherent structures like vortices and eddies being of particular importance to the underlying flow field. In addition, the modes can serve as a basis for a reduced-order model, thus, the original dynamical system can be projected onto a modeled system with fewer degrees of freedom. In contrast to a model-based approach, a data-driven technique like DMD offers the advantage that no information about the underlying, mostly non-linear and high-dimensional dynamical system is needed. The DMD algorithm used in this study was initially developed by Schmid [21], including an economy-sized singular value decomposition (SVD) to guarantee a more robust calculation in case of an ill-conditioned input data set. As usual for data-driven techniques, the DMD algorithm requires a sequence of equidistantly sampled snapshots arranged in form of the data matrix \(\psi _0 = \{\psi _1,\psi _2,\ldots ,\psi _{N}\}\), where \(\psi _{n}:=\psi (x,y,z,t_n)\) represents the high-dimensional flow field at the discrete time step \(t_n\). The DMD algorithm projects the data matrix onto a set of non-orthogonal spatial modes:

$$\begin{aligned} \underbrace{ [\psi _0\;\psi _1\;\dots \; \psi _{N-1}]}_{\varvec{\psi }_0}\approx \underbrace{ [\phi _1\;\phi _2\;\cdots \;\phi _N]}_{\Phi } \cdot \nonumber \\ \cdot \underbrace{ \begin{pmatrix} a_1&{} &{} &{} \\ &{} a_2&{} &{} \\ &{} &{}\ddots &{} \\ &{} &{} &{} a_N \end{pmatrix}}_{D_a=diag\{a\}} \underbrace{ \begin{pmatrix} 1&{}\quad \mu _1 &{}\quad \cdots &{}\quad \mu _1^{N-1}\\ 1&{}\quad \mu _2&{}\quad \cdots &{}\quad \mu _2^{N-1} \\ 1&{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 1&{}\quad \mu _N&{}\quad \cdots &{}\quad \mu _N^{N-1} \end{pmatrix}}_{V_{\mathrm{and}}}. \end{aligned}$$
(3)
Fig. 4
figure 4

Flow topology of the time-averaged LES results of the reference configuration, projected streamlines, and streamwise velocity contours

Full size image
Fig. 5
figure 5

Instantaneous distribution of the spanwise vorticity in the center cross section of the computational domain (\(z/h=2\)) of the reference configuration

Full size image

The quantity \(\phi _n\) is the spatial modes, \(a_n\) the amplitude of the corresponding DMD mode, and \(V_{\mathrm{and}}\) the Vandermonde matrix containing the eigenvalues \(\mu _n\), which determine the temporal evolution, i.e., the frequencies and decay rates of the modes. To determine the unknown amplitudes \(a_n\), the following convex optimization problem is solved

$$\begin{aligned} \underbrace{\mathrm {minimize}}_{a}\; \Vert \varvec{\psi }_0 - \Phi D_a V_{\mathrm{and}} \Vert _F^2. \end{aligned}$$
(4)

This means that the amplitudes are chosen, such that the entire input data sequence is optimally approximated. To reconstruct the temporally developing flow field, the entire or a subset of the DMD modes can be superimposed according to the following equation:

$$\begin{aligned} v(x,y,z,t)=\sum _{n=1}^N a_n e^{(\lambda _n t)}\phi _n(x,y,z). \end{aligned}$$
(5)

The quantity \(\lambda _n\) is the complex frequency which is determined by the following:

$$\begin{aligned} \lambda _n=\dfrac{\log \left( \mu _n\right) }{\Delta t}=\underbrace{\dfrac{\log \vert \mu _n\vert }{\Delta t}}_{D_n}+\,i \cdot \underbrace{ \arctan \left( \dfrac{\mu _{n,\mathrm{imag}}}{\mu _{n,\mathrm{real}}}\right) \dfrac{1}{\Delta t}}_{\omega _n}, \end{aligned}$$
(6)

where the real part \(D_n\) is the decay rate and the imaginary part \(\omega _n\) is the angular frequency of the respective mode. To select the DMD modes capturing the most important dynamic structures the sparsity-promoting algorithm introduced by Jovanovic et al. [12] is applied. Within the algorithm, sparsity is induced by adding an additional term to the objective function in Eq. 4 that penalizes the \(l_1\)-norm of the vector of the DMD amplitudes. The following optimization problem is obtained:

$$\begin{aligned} \underbrace{\mathrm {minimize}}_{a}\; \Vert \varvec{\psi }_0 - \Phi D_a V_{\mathrm{and}} \Vert _F^2+\gamma \sum _{i=1}^N \vert a_i \vert , \end{aligned}$$
(7)

where the positive regularization parameter \(\gamma\) specifies the relative emphasis on the sparsity of the vector a. The quantity \(\gamma\) can be used to trade off between the approximation error with respect to the full data and the number of extracted modes. For a more detailed description of the DMD and sparsity-promoting DMD algorithm, the reader is referred to Schmid [21] and Jovanovic et al. [12].

3 Results

The discussion of the results is divided into three parts. First, the general characteristics of the computed wake flow of the investigated configuration are described in detail and compared to the results of the reference configuration without flow control. Subsequently, the dynamic behavior of the wake flow is investigated using a classical statistical analysis, i.e., Fourier transformation. Finally, a DMD analysis of the wake flow is performed to detect spatio-temporal modes which are responsible for the dominant peaks found in the spectral analysis.

3.1 Characteristics of the wake flow topology

First, the flow field of the reference configuration is described. To visualize the flow topology along the investigated configuration, Fig. 4 shows the streamwise velocity distribution and characteristic streamlines of the time and spanwise averaged LES results. Additionally, the instantaneous spanwise vorticity distribution at the center cross section of the computational domain at \(z/h=2\) is given in Fig. 5. At the backward-facing step, the incoming fully developed turbulent boundary layer separates, such that a turbulent free shear layer develops. The turbulent structures grow and the intensity is increased due to vortex pairing while traveling downstream. The shed shear layer impinges on the nozzle wall between \(4 \le x_r/h \le 9\) depending on the spanwise position and time. Averaged over time, the reattachment position is \(x_r/h=7\). Figure 4 reveals that a large recirculation region is formed downstream of the BFS and a secondary recirculation region exists near the corner of the BFS.

Fig. 6
figure 6

Flow topology of the time and spanwise averaged LES results of the boat tail configuration, projected streamlines, and streamwise velocity contours

Full size image
Fig. 7
figure 7

Instantaneous distribution of the spanwise vorticity in the center cross section of the computational domain (\(z/h=2\)) of the boat tail configuration

Full size image
Fig. 8
figure 8

Flow topology of the time-averaged LES results, including a contour for the streamwise velocity at \(u/u_\infty =-\,0.01\) colored by the vertical distance from the nozzle surface to visualize the recirculation region and streamwise velocity contours at \(z/h=1.6\)

Full size image

To investigate the effect of the boat tail, the same quantities just discussed for the reference configuration are given for the boat tail geometry in Figs. 6 and 7. At the leading edge of the boat tail, the turbulent boundary layer separates, yielding a turbulent free shear layer. Similar to the reference configuration, the shear layer grows due to vortex paring and impinges on the nozzle wall between \(2 \le x_r/h \le 5\). Figure 6 reveals that the mean reattachment position is \(x_r/h=3.5\). Like in the reference configuration, a large primary recirculation region and a secondary recirculation region develop. Additionally, a further recirculation region is present at the taper of the main body. Comparing the results with the reference configuration, it is obvious that due to the boat tail geometry, the flow is redirected at the convex corner to the centerline of the configuration. The flow separates; however, under the current flow conditions, only a thin slender separation bubble develops. At the edge of the base, i.e., at \(x/h=0\), a pronounced normal momentum flux exists. As a result, the reattachment length of the shear layer and the size of the recirculation region is reduced by about 50% compared to the reference configuration.

Next, the topology of the time-averaged flow field of the configuration with lobes is presented. Figure 8 shows several characteristic streamlines and contours of the streamwise velocity component in the \(z/h=1.6\) cross section. The recirculation region is visualized by a contour of the streamwise velocity \(u/u_\infty =-\,0.01\) colored by the vertical distance from the nozzle surface. The intersection line of the velocity contour with the nozzle wall visualizes the reattachment of the flow and illustrates that averaged over time, the shed shear layer impinges on the nozzle wall between \(x_r/h\approx 1.3\) and \(x_r/h\approx 2.3\) depending on the spanwise position. Recalling that the mean reattachment length of the reference case without flow control is \(x/h=7\) [27], it is substantially reduced by more than 75% due to the lobes. In contrast to the reference case, the present configuration exhibits a pronounced three-dimensionality of the mean flow field characterized by the development of ellipsoidal reverse flow areas in the wake positioned in the spanwise direction between two adjacent lobes. A closer look at the streamlines shows that a part of the incoming boundary layer expands into the lobes, separates at the tail of the lobes, and flows straight to interact with the nozzle surface. At a streamwise position of about \(x/h=2\), this part of the flow possesses a strong spanwise velocity component, such that pronounced streamwise vortices develop. To further discuss the spanwise variation of the separating and reattaching flow field, the following notation is introduced. The spanwise position of the lobe center is called “in-lobe” (in) and the position exactly between two lobes “in-between lobes” (ib).

A more detailed visualization of the flow field is given in Figs. 9 and 10. The streamwise velocity contours and the projected streamlines of the time-averaged LES results and the instantaneous distribution of the spanwise vorticity are shown in the distinctive cross sections defined above.

Fig. 9
figure 9

Flow topology of the time-averaged LES results of the configuration with lobes, projected streamlines, and streamwise velocity contours

Full size image

The streamlines in the in-lobe cross section reveal that in contrast to the boat tail configuration, the incoming boundary layer is able to follow the deflection of the wall and does not separate upstream of the trailing edge of the lobe. Additionally, the considerable reduction of the recirculation region and reattachment length compared to the reference case is apparent. At this spanwise position, the maximum reverse flow velocity is about \(\langle u \rangle /u_\infty =-0.09\) and thus less than half the value of the reference case being \(\langle u \rangle /u_\infty \approx -0.25\).

The substantially reduced recirculation area and reverse flow velocity may lead to a change in the absolute nature of the flow which is highly dependent on the backflow intensity [17]. Weiss et al. [32] identified in an axisymmetric turbulent separating/reattaching flow a linearly absolute unstable area around the center of the recirculation region leading to an azimuthal antisymmetric mode of \(Sr_D=0.2\). By active flow control applied in the localized unstable area, a 50% reduction of the spatial area, where the maxima of the backflow are located, and a decrease of the magnitude of these maxima by 10% were achieved in Weiss and Deck [31]. By means of a spectral analysis, it was shown that the spatial broadband area of energy at the characteristic frequency of \(Sr_D=0.2\) reported in the uncontrolled case disappeared due to the control. It was assumed in their conclusions that these findings are related to a change of the nature of the instability transitioning from a fully absolute to a fully convective instability. To investigate, if a change in the absolute nature of the flow occurs in the present investigation, it would be necessary to perform a stability analysis in future work.

As shown in Fig. 8, the wake is characterized by a highly three-dimensional flow, i.e., the overall flow field between the lobes changes substantially. The flow separating from the BFS in the in-between lobes cross section does not reattach and thus no typical recirculation region occurs. The reverse flow region extends downstream to approximately 2.3h and the maximum backflow velocity is similar to that of the reference case. Another difference is that while a pronounced secondary recirculation region in the corner of the BFS is apparent in the reference case and the boat tail configuration, there is no or only a small secondary motion in the configuration with lobes.

To prove the working mechanism of the lobes to produce streamwise counterrotating vortices, the mean velocity vector field and the streamwise vorticity in the zy-plane at \(x/h = 0\) are shown in Fig. 11. Note that only one-third of the spanwise extent of the total computational domain is shown in the figure. The formation of two streamwise counterrotating vortices inside the lobe is clearly visible.

Fig. 10
figure 10

Instantaneous distribution of the spanwise vorticity in the in-lobe and in-between lobes cross sections

Full size image
Fig. 11
figure 11

Time-averaged distribution of the streamwise vorticity and velocity vector field in the yz-plane at \(x/h=0\)

Full size image

The instantaneous vorticity distribution in Fig. 10 indicates that due to the streamwise vortices, the turbulent mixing downstream of the lobes and thereby the spreading rate of the shear layer is increased. This qualitative statement is substantiated by the detailed discussion of the streamwise evolution of the vorticity thickness in Fig. 12 which allows a quantitative comparison of the spatial growth of the separated shear layer. This mechanism, which is caused by the upstream local convex deflection of the flow, explains the previously observed substantial reduction of the reattachment length in the in-lobe cross section. Additionally, the intensity of the turbulent structures in the area at \(x/h=2{-}3\) is increased, since the aforementioned three-dimensionality of the flow field enhances the turbulent production due to the strong mean velocity gradients.

Fig. 12
figure 12

Streamwise development of the vorticity thickness downstream of the BFS. The respective mean reattachment position of the different configurations is marked by \(x_r\)

Full size image

For a quantitative evaluation of the flow field, the distribution of the pressure along the nozzle wall is given in Fig. 13a. The distributions in the in-lobe and in-between lobes cross sections for the lobe case and the spanwise averaged findings for the boat tail and the reference configurations are depicted. The separation of the fully developed boundary layer at the BFS results in a pressure drop at the base. In the reference configuration, the pressure decreases from \(\langle p \rangle /p_\infty =0.95\) at the front of the main body at \(x/h=-\,10\), not shown here, to \(\langle p \rangle /p_\infty \approx 0.88\) at the base. The wall pressure remains at this low level up to \(x/h=3\) and increases to a value slightly above the freestream pressure further downstream due to the impingement of the separated shear layer on the nozzle surface. In comparison to the reference case, the base pressure is increased in both configuration with flow control leading to a reduced base drag. Even in the in-between lobes cross section, where the wall contour is formed like a standard backward-facing step, the base pressure is higher compared to the reference geometry. This is due to the upstream impact of the lobes occurring due to the transonic flow conditions and the three-dimensional character of the wake. The recompression caused by the impingement of the shear layer occurs in a smaller streamwise region and is shifted upstream due to the strongly reduced reattachment length. Figure 13b shows the pressure distribution at the end of the main body for the different configurations. Due to an acceleration of the flow towards the leading edge of the lobes and the boat tail, the pressure is significantly reduced. Further downstream, a continuous recompression towards the tail of the main body is visible.

Fig. 13
figure 13

Streamwise distribution of the mean wall pressure along the nozzle wall (a) and at the end of the main body (b); comparison of the various configurations

Full size image

As discussed in the introduction, the reason for the accelerated reattachment process in the lobe configuration is an increased shear-layer growth rate caused by streamwise vortices which are generated by the semi-circular lobes. These enhance the mixing and consequently the entrainment of the shear layer directly downstream of the step. To quantify the spatial growth of the separated shear layer, the vorticity thickness or velocity-profile maximum-slope thickness as it is called by Brown and Roshko [3] is calculated as a function of the streamwise position. The streamwise distribution of the vorticity thickness \(\delta _w\left( x\right)\)

$$\begin{aligned} \delta _w\left( x\right) =\frac{u_{\infty }- \langle u\rangle _{\mathrm{min}}(x)}{\left. \text {{max}}\left( \frac{\partial \langle u\rangle \left( x,y\right) }{\partial y}\right) \right| _{x}}, \end{aligned}$$
(8)

is plotted for the configurations in Fig. 12. In addition, the vorticity thickness growth rate \(\delta _w'=\partial \delta _w/\partial x\) for a plane mixing layer at constant density derived by the empirical law \(\delta _w' = 0.18(1-r)/(1+r)\) with \(r=U_2/U_1\approx \langle u \rangle _{\mathrm{min}}/U_\infty = -0.2\) [3] is illustrated. Note that in the configuration with the boat tail and the lobes, the shear layer separates at an angle with respect to the horizontal. Therefore, the velocity derivative is not calculated with respect to the y-axis as given in Eq. 8 but with respect to an axis perpendicular to the shear layer. In the reference configuration, the vorticity thickness grows linearly in the range \(0 \le x/h \le 3\) with the same rate like a planar shear layer. Further downstream, the shear layer approaches the nozzle wall leading to a restriction of its growth which can be seen in the reduced slope of the vorticity thickness distribution downstream of \(x/h=3\). After reaching its maximum value of \(\delta _w/h\approx 0.9\) at around the mean reattachment position, the vorticity distribution abruptly drops by more than one order of magnitude which is caused by the development of a new attached boundary layer [27].

The configuration with lobes exhibits an initial vorticity thickness growth rate that is more than twice as large as in the reference configuration in the in-lobe cross section. This confirms the aforementioned increased shear layer growth rate caused by the streamwise vortices generating the enhanced mixing. Similar to the configuration without flow control, the growth rate decreases as soon as the shear layer approaches the nozzle wall and drops to a value of almost zero downstream of the reattachment point. In the in-between lobes cross section, the growth of the shear layer is restricted by the spanwise directed crossflow at \(x/h = 2\). As a result, the evolution of the vorticity thickness is similar to that of the reference configuration just downstream of the BFS and features a reduced slope in the area of the crossflow. For the boat tail configuration, the increase of the vorticity thickness is shifted upstream due to the separation of the boundary layer at the leading edge of the taper. Note that the flow in the in-lobe cross section does not detach which is why \(\delta _w/h\) starts growing not before \(x/h=0\). Compared to the reference configuration, the vorticity thickness growth rate of the boat tail geometry is slightly higher coinciding with enhanced shear layer instabilities. After linearly increasing up to a value of \(\delta _w/h\approx 0.8\), the further growth is again restricted by the nozzle wall and the vorticity thickness drops to nearly zero after reattaching at \(x/h=3.5\).

Since the lobe configuration exhibits the strongest reduction of the reattachment length, i.e., it is the most promising configuration, the following investigations will focus only on the comparison of this and the reference geometry.

Fig. 14
figure 14

Streamwise distribution of the rms value of the pressure fluctuations: comparison of the configuration with and without flow control

Full size image

To gain a first impression of the dynamic loads on the nozzle, Fig. 14 depicts the rms value of the pressure fluctuations for the reference and the lobe configuration. First, the distribution of the pressure fluctuations along the nozzle wall at \(0<x/h<10\) is discussed. For the reference configuration, the pressure fluctuations reach values of about \(p'_{\mathrm{rms}}/p_\infty =0.009\) up to \(x/h=3\). Further downstream, the pressure fluctuations reach a plateau with a value of \(p'_{\mathrm{rms}}/p_\infty =0.015\). The increase is caused, on the one hand, by small-scale turbulent structures in the separated shear layer impinging on the nozzle surface at the reattachment position, and, on the other hand, by large spatio-temporal coherent structures in the separation region, which were identified by Statnikov et al. [27]. For the lobe configuration, the rms value of the pressure fluctuations at the base of the BFS is only half of the value of the reference configuration. This lower value is most likely caused by the absence of a secondary recirculation region. At the mean reattachment position, the pressure fluctuations are substantially increased and reach values more than 30% higher than the value of the reference configuration in the in-between lobes cross section and more than twice of the reference value in the in-lobe cross section. Far downstream of the reattachment position, the pressure fluctuations decrease and reach the same value as in the reference case. The higher fluctuations in the in-lobe cross section are likely to be caused by an increased intensity of the small-scale turbulent structures due to the spanwise velocity variation and the larger impingement angle on the nozzle wall. In the in-between lobes cross section the fluctuation growth can be also explained by the flow deflection in the spanwise direction at about \(x/h = 2\). In this region, high velocity gradients enhance the turbulence production and thus the amplitude of the pressure fluctuations. In addition, the flow carries turbulent structures towards the in-between lobes cross section.

Upstream of the BFS at \(-2<x/h<0\), especially in the in-lobe cross section, the pressure fluctuations are increased by the intensified vorticity caused by the counterrotating vortices in the lobes.

3.2 Spectral analysis of the wake flow dynamics

Since the rms values of the pressure fluctuations only allow a limited assessment of the dynamic loads, the power spectral densities (PSD) of the wall pressure signal at several streamwise positions are shown in Fig. 15. The PSD analysis of the configuration with lobes is based on time-resolved data comprising a time interval of \(204.8\, t_{\mathrm{ref}}\). Using a sampling frequency of \(Sr_D = 10\) and a window width of \(102.4\,t_{\mathrm{ref}}\), frequencies in the range of \(9.8 \times 10^{-3}<Sr_D<5\) can be determined according to the Nyquist criterion.

Fig. 15
figure 15

Power spectral density of the wall pressure fluctuations \(p'/p_\infty\) at several streamwise positions for the lobe and reference configuration

Full size image

At the streamwise positions \(x/h= 5 \text { and } 7\), where the product of the lever arm and the pressure fluctuations and thereby the resulting dynamic moments are largest, the spectra given in Fig. 15a reveal that the low-frequency pressure fluctuations and hence the undesired dynamic forces, which are responsible for the buffeting phenomenon, are reduced due to the semi-circular lobes. However, this reduction is achieved at the expense of increased high-frequency pressure fluctuations at \(Sr_D\ge 0.4\). Since the maximum fluctuations now occur at higher frequencies, the influence on the stability of the structure is likely to be reduced. At the mean reattachment positions of the configuration with lobes in Fig. 15b, where the lever arm of the pressure fluctuations and thereby the effect on the thrust nozzle is small, the low-frequency pressure fluctuations are of the same magnitude as in the reference configuration. Again, the high-frequency pressure fluctuations with \(Sr_D \ge 0.4\) are significantly increased due to the presence of the semi-circular lobes. This confirms the previous statement that the intensified small, high-frequency turbulent structures in the separated shear layer are primarily responsible for the increased pressure fluctuation rms values in the configuration with lobes.

Fig. 16
figure 16

DMD spectrum of the three-dimensional streamwise velocity field. Eigenvalues \(\mu _n=e^{(\lambda _n \Delta t)}\) (a). Amplitude-distribution versus frequencies \(\mathfrak {I}(\lambda _n)\) (b). The dominant modes in terms of the sparsity-promoting DMD are marked by filled symbols

Full size image

As shown by Statnikov et al. [27], the PSD of the reference configuration contains two pronounced temporal scales at \(Sr_D= \{0.04;0.23\}\). A DMD analysis evidenced that the low-frequency oscillation belongs to a coherent longitudinal cross-pumping motion of the recirculation region and the second temporal scale originates from a cross-flapping motion of the separated shear layer. Due to those two coherent motions, the longitudinal expansion of the recirculation bubble alternates between four and nine step heights. Additionally, the reattachment line is not straight but exhibits an elongated finger-like shape alternating in time and span. The two extracted spatial DMD modes feature a spanwise wave length of two step heights.

In the spectra of the wall pressure fluctuations at the mean reattachment position of the configuration with lobes, three distinct peaks at \(Sr_D= \{0.04;0.11;0.22\}\) can be identified in the in-lobe and in-between lobes cross sections. To understand the underlying flow phenomena leading to this periodic behavior, a dynamic mode decomposition is conducted to extract dominant spatio-temporal modes from the time-resolved three-dimensional flow field.

3.3 Modal analysis

The dynamic mode decomposition is performed using 300 snapshots of the three-dimensional streamwise velocity field of the wake. The snapshots are equidistantly sampled with a sampling frequency of \(Sr_D=10\). Using the full resolution, the snapshot matrix would include approximately \(10^{11}\) entries, requiring nearly 1 TB of storage which is quite a challenge for the DMD algorithm. Therefore, only the interesting part of the domain enclosing the wake is used for the analysis and each second point in the wall-normal and the streamwise direction is skipped reducing the number of entries in the snapshot matrix to roughly \(10^{10}\) and the needed storage to 165 GB. The DMD algorithm is parallelized using MPI and ScaLAPACK and the I/O is performed using the HDF5 parallel file format. The resulting DMD spectrum is shown in Fig. 16. In Fig. 16a, the complex DMD eigenvalues \(\mu _n\) are plotted along with the unit circle to enable the assessment of the decay rates. In Fig. 16b, the amplitudes \(a_n\) of the DMD modes normalized by the amplitude \(a_{\mathrm{mean}}\) of the mean mode are shown as a function of their dimensionless frequency \(Sr_D=\mathrm{Im}(\lambda _n)/(2\pi \Delta t)\). Three DMD modes, i.e., \(\lambda _1, \lambda _2, \lambda _3\), selected by the sparsity-promoting algorithm by Jovanovic et al. [12], are marked by red dots. The eigenvalues of these three modes are located closest to the unity circle evidencing that these modes are the most stable modes which contribute most notably to the analyzed data sequence. The other modes which exhibit an initially larger amplitude show a larger decay rate leading to a minor contribution to the overall processed data. The dimensionless frequencies of the extracted modes are \(Sr_D (\lambda _1)=0.043\), \(Sr_D (\lambda _2)=0.111\), and \(Sr_D (\lambda _3)=0.219\) coinciding with the characteristic frequencies of the PSD spectra of the pressure fluctuations shown in Fig. 15b.

To visualize the three-dimensional shape belonging to the respective frequency \(\lambda _n\), the spatial modes \(\phi _n\) are superimposed with the mean mode \(\phi _{\mathrm{mean}}\) and reconstructed in time according to Eq. 5. An instantaneous snapshot of the reconstructed streamwise velocity field is given for the three modes in Fig. 17. Figure 17a shows that the extracted low-frequency mode at \(Sr_D(\lambda _1)=0.043\) belongs to a coherent longitudinal pumping motion of the separation bubble illustrated in the sketch. More precisely, the underlying fluid motion of this mode is a periodically growing and shrinking of the separation bubble in the streamwise direction with an amplitude of about half a step height. The center frequency mode \(Sr_D (\lambda _2)=0.111\) in Fig. 17b describes a pulsating motion of the recirculation region that is defined by a periodical swelling and shrinking of the separation bubble in the spanwise direction. The flow field reconstruction of the third selected DMD mode \(Sr_D (\lambda _3)=0.219\) is given along with a sketch of the underlying dynamic motion in Fig. 17c. The temporal development of the superimposed spatial modes \(\phi _3\) and \(\phi _{\mathrm{mean}}\) reveals a formation of snake-like structures oscillating in the spanwise direction in time.

A common characteristic of the three extracted DMD modes is the spatial periodicity in the spanwise direction featuring a wave length that is equal to the distance between two lobes, i.e., 1.6 step heights. When comparing the DMD modes with those of the reference configuration described in Ref. [27], it is quite clear that the large-scale coherent structures identified in the reference case can be influenced by the geometry of the lobes. More precisely, the spanwise oscillation in the reference case at a wave length of two step heights is suppressed, only modes featuring a wave length of 1.6 step heights occur. Furthermore, the reattachment length of the configuration with lobes varies only by half a step height in time. That is, the strong oscillatory behavior of the reattachment line in the reference case is reduced.

Fig. 17
figure 17

Reconstruction of the wake by superposition of the DMD mode and the mean mode. The recirculation region is visualized by a contour for the streamwise velocity at \(u/u_\infty =0.25\) colored by the distance from the nozzle surface

Full size image

4 Conclusions and outlook

The influence of two passive flow control methods on the turbulent wake of a planar generic space launcher at transonic speed is investigated and compared to a standard backward-facing step geometry by a zonal RANS/LES approach and dynamic mode decomposition. It is shown that for a classical boat tail, the reattachment length of the shed turbulent shear layer is reduced by 50% due to enhanced shear layer instabilities leading to an increased shear layer growth rate. For the second approach, consisting of semi-circular lobes distributed along the trailing edge of the main body, a reduction of the reattachment length by approximately 75% is achieved. The reason for the more upstream reattachment is traced back to an increased shear layer growth caused by an enhanced turbulent mixing and to an attached boundary layer along the taper.

The evaluation of the wall pressure on the nozzle reveals an increase of the rms value of the pressure fluctuations around the reattachment position for the lobe configuration. Using classical statistical analysis, i.e., temporal Fourier transformation, it is shown that in the region, where the pressure fluctuations exhibit a large lever arm, the low-frequency fluctuations causing the undesired buffet loads are reduced due to the lobes. However, this reduction is obtained at the expense of increased high-pressure fluctuations which are most probably of minor importance for the structure.

The spectra of the pressure fluctuations reveal three characteristic frequencies at \(Sr_{D,1}=0.04\), \(Sr_{D,2}=0.11\), and \(Sr_{D,3}=0.22\). The underlying coherent fluid motion responsible for the detected pressure oscillations is identified by dynamic mode decomposition of the streamwise velocity field. Three DMD modes at \(Sr_D(\lambda _1)=0.043\), \(Sr_D (\lambda _2)=0.111\), and \(Sr_D (\lambda _3)=0.219\) closely matching the peaks of the pressure spectra are extracted by the sparsity-promoting algorithm by Jovanovic et al. [12]. The temporal reconstruction of the extracted spatial modes reveals a periodic streamwise pumping, a spanwise pulsating, and a snake-liked oscillation belonging to the respective frequencies. The comparison of the DMD modes of the lobe configuration to those of the reference case reveals that the longitudinal cross-pumping and cross-flapping motion with a spanwise wave length of two step heights can be eliminated by the lobes. It is further shown that the spanwise wave length of the large-scale coherent structures in the wake can be obviously triggered by the spatial distance between the lobes.

As discussed in the introduction, Deck and Thorigny [4] observed an antisymmetric mode in the azimuthal direction in the turbulent wake of an axisymmetric Ariane 5-like generic launcher configuration caused by ordered large-scale coherent structures in the wake. This antisymmetric mode with a critical frequency of \(Sr_D=0.2\) is the origin of lateral dynamic side loads acting on the thrust nozzle which are critical for the strength and stability of the structure. Taking into account the above described capability of the lobes to influence the coherent structures, the lobes might be able to reduce or even suppress the critical side loads observed in the axisymmetric configuration. The effect of the semi-circular lobes on the turbulent wake of an axisymmetric space launcher configuration and their potential ability to prevent the occurrence of side loads is the subject of ongoing research activities.