1 Introduction

Angular contact ball bearings (ACBB) are commonly used as core components in spindle systems and play a vital central role, with excellent properties such as low friction coefficient, simple structure, high operating accuracy and cost effectiveness [1, 2, 29]. Its dynamic characteristics directly affect the machining accuracy of the spindle system, so it is of great significance to analyze and evaluate the dynamic characteristics of the bearing to improve the accuracy and stability of the spindle system [3]. However, under high-speed conditions, the internal temperature of the bearing increases significantly, resulting in thermal expansion of the internal components and affecting the contact state between the inner ball of the bearing and the inner/outer raceway [4, 5, 9, 21]. The thermal expansion generated by this temperature rise will not only change the dynamic characteristics of the bearing system, but also affect its vibration behavior, and further affect the machining accuracy of the spindle system [6, 7]. Therefore, it is imperative and crucial to investigate the impact of temperature on the dynamic characteristics of ACBB and develop a control strategy for bearing thermal properties in order to regulate the vibration state of the spindle system.

By applying a preload force to the spindle system, the internal clearance and elastic deformation can be effectively reduced, thereby enhancing its stability and mitigating vibration behavior [8]. Under high-speed conditions, the thermal induced preload [5, 9, 21] caused by spindle system thermal expansion due to temperature rise will interact with the initial preload, thereby affecting load distribution, stiffness, and bearing vibration characteristics [5, 6, 9, 10, 21]. According to the preload mechanism of the spindle system, [11, 13] found that the thermal induced preload caused by thermal expansion has an important influence on the dynamic and thermal characteristics of the system. Sun et al., [12] found through research that the temperature of the inner ring of the spindle bearing is higher than that of the outer ring, and the heat generation of the inner ring is significantly affected by the preload force and speed. Li et al., [11, 13] analyzed the influence of temperature on the dynamic characteristics of the spindle system, and obtained the influence law that with the increase of temperature, the preload caused by the thermal deformation of the bearing also increased correspondingly. Zhang et al., [14] proposed a method to control the initial axial preload in real time by changing the control structure of the preload by using the preload mechanism of piezoelectric actuators (PEAs). Li et al., [15] investigated the dynamic behavior of an electric spindle system under varying temperature conditions, computed the thermal-induced preload of the spindle bearing at different temperature levels, and determined its impact on bearing stiffness.

To adapt to a wider range of working conditions, the spindle system must maintain high-precision rotation while the rotor increases stiffness and reduces vibration during high-speed rotation, ensuring stable operation of the spindle system [16]. Under practical working conditions, thermal expansion has emerged as a critical factor impacting the performance of angular contact bearings. Maurya et al., [17] found that the thermal expansion of rotating ball bearings could not be completely eliminated by thermal compensation and control. Dai et al., [18, 19] analyzed the heat transfer mechanism inside the high-speed motorized spindle, proposes a non-uniform preload regulation method, and establishes an adjustable preload platform. Therefore, it is necessary to comprehensively consider the joint influence of the working state of the bearing and the thermal preload caused by thermal expansion on its stiffness. Truong et al., [6, 20] took the thermal expansion of angular contact ball bearings into account and calculates its stiffness matrix. The results show that the temperature rise has a significant effect on the bearing stiffness, and the thermal effect can greatly increase the stiffness coefficient. Dong et al., [5, 9, 21] proposed an online monitoring method for the thermal stiffness of the spindle system based on fiber Bragg grating sensor network, analyzed the relationship between temperature rise, thermal preload force and thermal stiffness, and obtained the need to adopt thermal preload force to improve the thermal stiffness of the spindle system. Jiang et al., [22] investigated the impact of various preloads on the stiffness of the main shaft bearing and found a positive correlation between bearing stiffness and preload.

In high-speed working conditions, the spindle bearing inevitably produces vibration phenomena. To enhance the machining accuracy of the spindle system, measures must be taken to reduce its vibrational behavior. Liu et al., [23, 24] established the rotor-bearing system dynamics model, analyzed the bearing vibration signals under the vibration interaction, and diagnosed and identified the fault signals. According to the bearing dynamic model and the thermal effect, [23, 24] analyzed the bearing vibration response under different fit clearance, and the results showed that the bearing clearance had a strong correlation with vibration. The internal components of the spindle system undergo thermal expansion due to temperature rise, resulting in changes in the internal contact state of its bearings, which in turn affects the vibration characteristics of the entire system [25, 26]. Zhang et al., [27] established a thermodynamic coupling model of the ceramic electric spindle, and analyzed the vibration characteristics of the spindle bearing, taking into account factors such as temperature, speed and preload. The results show that the vibration can be effectively inhibited by adjusting the bearing preload. Wang et al., [28] established a bearing dynamic model considering raceway defects and studied the influence of thermal effects on spindle bearing vibration characteristics based on thermal elastohydrodynamic lubrication. The results show that the vibration amplitude of bearing will increase due to thermal effect. By analyzing the “over-slip” behavior of bearings, [1, 29] found that there is a close correlation between the vibration response of bearings and the behavior. Chang et al., [30] studied the relationship between the vibration characteristics of the spindle rotor and bearing temperature, and found that the thermal expansion inside the bearing would lead to clearance changes, resulting in more complex motion phenomena. In fact, the current research on the vibration characteristics of spindle bearings mainly focuses on the establishment of bearing dynamics models [31, 32]. However, few scholars have established a correlation between temperature, stiffness and vibration and developed effective measures to mitigate system vibration.

In summary, the temperature significantly impacts the dynamic characteristics of the main shaft bearing due to thermal expansion inducing changes in internal contact state and subsequent alterations in stiffness and vibration properties. To enhance spindle system machining accuracy, effective measures must be implemented to suppress vibration behavior.

Therefore, to accurately assess the impact of thermal effects on spindle bearing dynamic characteristics, this paper proposes a dynamic model of angular contact ball bearings that takes into account temperature rise and thermal expansion. Based on raceway control theory [33] and Newton–Raphson iterative algorithm [34], the influence of temperature rises on bearing internal contact and stiffness characteristics was analyzed, and verified by finite element method. The impact of temperature on spindle system rigidity has been validated through a temperature rise test. Concurrently, experimental results demonstrate that temperature elevation can effectively mitigate spindle system vibration. This approach establishes the groundwork for enhancing spindle machining precision.

2 Ball Bearing Dynamic Model (BBDM)

To enhance the initial load capacity of the spindle system, it is imperative to apply an appropriate preload force on the angular contact ball bearing (ACBB) in a diagonal arrangement. This preload will have a direct impact on the dynamic performance of the spindle system, including vibration, temperature rise and stiffness. A higher preload can enhance stiffness and diminish vibration, whereas a smaller preload may impact load-carrying capacity [10, 35]. Furthermore, real-time axial preload and displacement are also influenced by external loads and thermal expansion. Thermal induced preload (TIP) is a result of the thermal displacement of internal bearing components due to thermal expansion, which is significantly impacted by initial preload [11, 13]. With an increase in initial preload, the TIP will experience a rapid rise, rendering traditional methods inadequate for precise stress control between bearing rings.

2.1 Temperature-Induced Bearing Elastic Deformation Analysis

In reality, the thermal expansion of bearing components can alter the internal state of a running bearing system [1, 29]. The actual size of the internal ball varies due to thermal expansion, which affects the contact load between the ball and both the internal and external raceways as temperature rises within the bearing. In this paper, temperature rise is a crucial factor that can be incorporated into analyzing contact deformation and load deflection parameters.

The sphere’s actual size Dt of the sphere and the thermal expansion εb are precisely defined as follows:

$$\left\{ {\begin{array}{*{20}c} {D_{t} = D \times \left( {1 + \upvarepsilon_{b} } \right)} \\ {\upvarepsilon_{b} = \frac{1}{2} \times \upalpha_{b} \times D \times \Delta T} \\ \end{array} } \right.$$
(1)

Here, αb is the ball thermal expansion coefficient, D is the ball diameter and ΔT is the uniform temperature of the ball.

Under high-speed, the inner and outer rings of the bearing move freely along the axial direction and the radial size are small, so the thermal deformation of the inner and outer rings of the bearing are ignored. This paper only considers the effect of thermal deformation caused by thermal expansion on the bearing rolling element.

2.2 The Thermal-Preload Controllable Method of ACBB

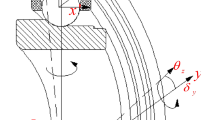
As shown in Fig. 1, under axial preload Fa, axial deviation δa occurs in the internal rolling ball of the bearing, and contact deformation δi(o) occurs between the ball and the inner and outer raceway, resulting in the distance between the center of curvature of the inner and outer raceway changing from BDt to s, and the initial contact angle changing from αo to αp. The ball-raceway contact deformation δi(o) and ball diameter Dt are varying with bearing temperature ΔT and the axial preload Fa. Bearing deformation is defined as follows:

$$\left\{ {\begin{array}{*{20}l} {BD_{t} = r_{i} + r_{o} - D_{t} } \hfill \\ {s = BD_{t} + \updelta_{i} + \updelta_{o} } \hfill \\ \end{array} } \right.$$
(2)
Fig. 1
figure 1

Bearing with preload: a static state; b under axial preload

Full size image

Here, BDt and s is the distance between the center of curvature of inner and outer raceway before and after dynamic loads, ri and ro are the curvature radius of the inner and outer raceway of the bearing respectively. Temperature rise can change the actual size Dt of the bearing ball, which in turn alters the internal geometric relationship of the bearing and affects its dynamic characteristics.

In the process of high-speed rotation of bearing, there are two loads and a gyroscopic moment acting on balls and inner ring of ball bearing as shown in Fig. 2. The first load P1 is due to the interference between the inner ring and shaft. The inner ring reduces P1 due to centrifugal movement when the spindle speed is increased, and then the influence of the first load P1 on the bearing interior can be ignored [35]. The second load P2 is the centrifugal force generated by the centrifugal movement of the bearing ball. The contact load Qi (o) and frictional force Ti (o) are caused by the gyroscopic moment Mg between ball and ring of bearing.

Fig. 2
figure 2

loads equilibrium of bearing: a loads acting on a ball; b load diagram of bearing interface; c loads acting on outer ring; d loads acting on a ball; e loads acting on inner ring

Full size image

According to loads equilibrium of bearing, the contact load Qij(oj) of the j-th ball has been obtained as follow by [35]:

$$\left\{ {\begin{array}{*{20}l} {Q_{ij} = P{2} \times \frac{{\sin \upalpha _{oj} }}{{\sin (\upalpha _{ij} - \upalpha _{oj} )}}} \hfill \\ {Q_{oj} = P{2} \times \frac{{\sin \upalpha _{ij} }}{{\sin (\upalpha _{ij} - \upalpha _{oj} )}}} \hfill \\ \end{array} } \right.$$
(3)

Here, αij and αoj are the contact angles between the j-th ball and the inner and outer raceways respectively.

If “outer raceway control” is approximated at given location, the ball gyroscopic moment Mgj of the j-th ball is resisted by friction force Toj = 2Mgj/Dt at outer raceway contact, and friction force Tij = 0 at inner raceway (Jones., 1960). For steel balls, the centrifugal force P2 and gyroscopic moment Mgj acting on a ball is calculated as follows in [2]:

$$P{2} = 2.26 \times 10^{ - 11} \times D_{t}^{3} \times n_{m}^{2} \times d_{m}$$
(4)
$$\left\{ {\begin{array}{*{20}l} {M_{gj} = J \times \left( {\frac{{\upomega _{R} }}{\upomega }} \right) \times \left( {\frac{{\upomega _{m} }}{\upomega }} \right) \times\upomega ^{2} \times \sin\upbeta } \hfill \\ {\frac{{\upomega _{R} }}{\upomega } = \frac{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {\left( {{{D_{t} \times \cos\upbeta } \mathord{\left/ {\vphantom {{D_{t} \times \cos\upbeta } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right)}}} \right. \kern-0pt} {\left( {{{D_{t} \times \cos\upbeta } \mathord{\left/ {\vphantom {{D_{t} \times \cos\upbeta } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right)}}}}{{\left( {\frac{{\cos \upalpha _{oj} + \tan\upbeta \times \sin \upalpha _{oj} }}{{1 + \left( {{{D_{t} } \mathord{\left/ {\vphantom {{D_{t} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right) \times \cos \upalpha _{oj} }}} \right) + \left( {\frac{{\cos \upalpha _{ij} + \tan\upbeta \times \sin \upalpha _{ij} }}{{1 - \left( {{{D_{t} } \mathord{\left/ {\vphantom {{D_{t} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right) \times \cos \upalpha _{ij} }}} \right)}}} \hfill \\ {\frac{{\upomega _{m} }}{\upomega } = \frac{{1 - \left( {{{D_{t} } \mathord{\left/ {\vphantom {{D_{t} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}} \right) \times \cos \upalpha _{ij} }}{{1 + \cos (\upalpha _{ij} - \upalpha _{oj} )}}} \hfill \\ {\upbeta = \arctan \left( {\frac{{\sin \upalpha _{oj} }}{{\cos \upalpha _{oj} + {{D_{t} } \mathord{\left/ {\vphantom {{D_{t} } {d_{m} }}} \right. \kern-0pt} {d_{m} }}}}} \right)} \hfill \\ \end{array} } \right.$$
(5)

Here, nm is the speed of the bearing, dm is the pitch diameter of the bearing, J is moment of inertia of bearing roller, and β is the pitch angle of the bearing roller.

Based on Fig. 2, considering the equilibrium of loads on the j-th ball in the horizontal and vertical directions:

$$\left\{ {\begin{array}{*{20}l} {Q_{oj} \times \sin \upalpha _{oj} - Q_{ij} \times \sin \upalpha _{ij} + 2 \times M_{gj} \times {{\cos \upalpha _{oj} } \mathord{\left/ {\vphantom {{\cos \upalpha _{oj} } {D_{t} }}} \right. \kern-0pt} {D_{t} }} = 0} \hfill \\ {Q_{oj} \times \cos \upalpha _{oj} - Q_{ij} \times \cos \upalpha _{ij} - 2 \times M_{gj} \times {{\sin \upalpha _{oj} } \mathord{\left/ {\vphantom {{\sin \upalpha _{oj} } {D_{t} - P{2}}}} \right. \kern-0pt} {D_{t} - P{2}}} = 0} \hfill \\ \end{array} } \right.$$
(6)

In Fig. 3, under an axial preload Fa > 0N, the centrifugal force P2 >  > 0N, the contact angles αij(oj) are dissimilar and not col-linear with BDt in (Jones., 1960). For the ball of bearing at any azimuth angle position φj, the distance between the final position of the center of the ball of bearing and inner (outer) raceway groove curvature center Δij(oj) is:

$$\left\{ {\begin{array}{*{20}l} {\Delta _{ij} = \left( {f_{i} - 0.5} \right) \times D_{t} +\updelta _{ij} -\upvarepsilon _{b} } \hfill \\ {\Delta _{oj} = \left( {f_{o} - 0.5} \right) \times D_{t} +\updelta _{oj} -\upvarepsilon _{b} } \hfill \\ \end{array} } \right.$$
(7)
Fig. 3
figure 3

Deformation relationship under loads condition between ball and raceway

Full size image

The calculation method of fi and fo is:

$$\left\{ {\begin{array}{*{20}l} {f_{i} = {{r_{i} } \mathord{\left/ {\vphantom {{r_{i} } {D_{t} }}} \right. \kern-0pt} {D_{t} }}} \hfill \\ {f_{o} = {{r_{o} } \mathord{\left/ {\vphantom {{r_{o} } {D_{t} }}} \right. \kern-0pt} {D_{t} }}} \hfill \\ \end{array} } \right.$$
(8)

For the ball of bearing at any azimuth angle position φj, the distance between the inner and outer raceway groove curvature center A1j(2j) is:

$$\left\{ {\begin{array}{*{20}l} {A_{1j} = BD_{t} \times \sin \upalpha^{o} + \delta_{a} + \upvarepsilon_{b} \times \sin \upalpha_{ij} } \hfill \\ {A_{2j} = BD_{t} \times \cos \upalpha^{o} + \updelta_{r} \times \cos \upvarphi_{j} + \upvarepsilon_{cent} = BD_{t} \times \cos \upalpha^{o} + \updelta_{r} \times \cos \upvarphi_{j} - \upvarepsilon_{b} \times \cos \upalpha_{ij} } \hfill \\ \end{array} } \right.$$
(9)

Here, δa is axial deformation and δr is radial deformation.

For the sake of analysis, new variables X1j and X2j are defined in Fig. 3:

$$\left\{ {\begin{array}{*{20}l} {\sin \upalpha _{ij} = \frac{{A_{1j} - X_{1j} }}{{\Delta _{ij} }},\cos \upalpha _{ij} = \frac{{A_{2j} - X_{2j} }}{{\Delta _{ij} }}} \hfill \\ {\sin \upalpha _{oj} = \frac{{X_{1j} }}{{\Delta _{oj} }},\cos \upalpha _{oj} = \frac{{X_{2j} }}{{\Delta _{oj} }}} \hfill \\ \end{array} } \right.$$
(10)

According to the Pythagorean theorem, the geometric relationship in Fig. 3, can list the equation:

$$\left\{ {\begin{array}{*{20}l} {(A_{1j} - X_{1j} )^{2} + (A_{2j} - X_{2j} )^{2} =\Delta _{ij}^{2} } \hfill \\ {X_{{_{1j} }}^{2} + X_{2j}^{2} =\Delta _{oj}^{2} } \hfill \\ \end{array} } \right.$$
(11)

In order to solve and calculate the unknowns X1j, X2j, δij, δoj, Mgj and P2, it is necessary to establish the equilibrium condition of the whole bearing. According to the “outer raceway control”, it is believed that the outer orbit of the bearing is fixed, so the contact area between the rolling ball of the bearing and the inner raceway needs to meet the mechanical equilibrium conditions. As shown in Fig. 1, and Fig. 2, the contact area between the rolling ball and the inner raceway is affected by the contact force Qij of the inner raceway, the friction force Tij, the first load P1 and the external axial preload Fa. According to the “outer orbit control theory”, the friction force Tij is 0; The first load P1 has little effect on the bearing interior and can be ignored. Then the balance equation of the whole bearing can be written as:

$$F_{a} - Z \times Q_{ij} \times \sin \alpha_{ij} = 0$$
(12)

Simultaneous Eqs. (3, 7, 10 and 12), then the bearing balance equation is:

$$F_{a} - Z \times \frac{{P{2} \times \frac{{\sin \upalpha _{oj} }}{{\sin (\upalpha _{ij} - \upalpha _{oj} )}} \times (A_{1j} - X_{1j} )}}{{(f_{i} - 0.5) \times D_{t} +\updelta _{ij} -\upvarepsilon _{b} }} = 0$$
(13)

After the ball bearing dynamic model is established, the Newton–Raphson method is used to solve X1j, X2j, δij, δoj, Mgj and P2. Simultaneous Eqs. (6–12) are solved using the numerical iterative algorithm flow is shown in Fig. 4, and obtain the contact angle αij and αoj of inner and outer raceway. At the same time, other main parameters of bearings can be calculated accurately, when the bearing is subjected to axial preload Fa, the axial deformation δa and the axial stiffness Ka \({K}_{a}\) are calculated as follows:

$$\left\{ {\begin{array}{*{20}l} {\delta_{a} = \frac{K}{{Z^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} \times \sin^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0pt} 3}}} \upalpha _{ij} }} \times F_{a}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} } \hfill \\ {K_{a} = \frac{{\partial F_{a} }}{{\partial \delta_{a} }} = \frac{{3 \times Z^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} \times \sin^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0pt} 3}}} \upalpha _{ij} \times F_{a}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}{2 \times K}} \hfill \\ \end{array} } \right.$$
(14)

where, K is the equivalent load deformation coefficient, the value of which depends on the geometric size and material constant of the contact point between the rolling body and the inner and outer raceway.

Fig. 4
figure 4

The flowchart of calculation process for model

Full size image

2.3 Simulation Analysis of Different Speed and Temperature

The angular contact bearing B7007C is selected as the simulated object, with the dimensions is shown in Table 1. The Newton–Raphson method is used to research the bearing under 5000 rpm and 10,000 rpm with temperature rise.

Table 1 Basic structural parameters of B7007C bearing
Full size table

As shown in Fig. 5a, b, the inner contact angle αi and the outer contact angle αo decrease gradually with the increase of the temperature rise. When the temperature rise is the same, with the increase of bearing speed, the inner contact angle αi presents an upward trend, while the outer contact angle αo presents a downward trend. When the bearing speed is constant, the bearing inner contact angle αi and the bearing outer contact angle αo present downward trend with the increase of bearing temperature rise.

Fig. 5
figure 5

Bearing variable with speed and temperature rise (Fa = 300 N) a inner contact angle; b outer contact angle; c inner contact force; d outer contact force; e stiffness

Full size image

At the same time, when the axial preload Fa is the same, the normal contact force Qi and Qo are proportional to temperature rise. In Fig. 5c, d, When the temperature rise is the same, with the increase of bearing speed, the inner contact load Qi presents a downward trend, while the external contact load Qo presents an upward trend. At 5000 rpm and 10,000 rpm, the external contact load Qo is larger than the inner contact load Qi. With the increase of temperature rise, the normal contact force Qi and Qo increase nonlinear.

As shown in Fig. 5e, when the axial preload Fa is the same, the bearing stiffness is proportional to temperature rise. The bearing stiffness increases gradually with the increase of the temperature rise. When the temperature rise is the same, with the increase of bearing speed, the bearing stiffness presents a downward trend. When the bearing speed is constant, the bearing stiffness presents an upward trend with the increase of bearing temperature rise.

In this paper, the impact of temperature elevation on bearing dynamic characteristics is investigated by integrating a theoretical model with temperature rise. However, due to potential limitations in the theoretical model, a thermodynamic coupling model for angular contact ball bearings was established using finite element analysis to examine the effects of temperature rise on ball contact characteristics. The research findings presented in this paper have been validated by comparison with the theoretical model, thus ensuring their reliability.

3 Thermodynamic Coupling Model

To validate the reliability of the theoretical model, this study established a thermodynamic coupling finite element model of angular contact ball bearing based on ANSYS Workbench, analyzed the change of the contact force between the internal ball and the raceway with the increase of the external temperature of the bearing, and compared the results with the theoretical model.

3.1 Finite Element Model Construction

Mesh division is a key step in finite element simulation, and the quality of mesh division directly affects the speed of analysis, the accuracy of analysis results and the time spent in analysis. Due to the irregular geometric structure of angular contact ball bearings, it is impossible to refine the mesh of the contact area directly, so the three-dimensional model needs to be segmented. In this paper, hexahedral mesh partitioning method is used to segment the bearings. The bearing inner (outer) raceway mesh size is 0.5 mm, the contact point neighborhood local mesh size is at least 0.1 mm, the farther away from the contact point, the mesh size gradually increases until the end of 0.5. The mesh size of the rolling body is 0.3 mm. The contact type between the rolling body and the inner (outer) track is selected as the face-to-surface contact. The contact surface of the rolling body is selected as the main surface, and the contact surface of the inner (outer) track is selected as the slave surface. The elastic modulus of the bearing material is 206 GPa, Poisson’s ratio is 0.3, the density is 7850 kg/m3, and the friction coefficient is 0.03.

The constraints on each part of the bearing are as follows: (1) The outer surface of the outer raceway of the bearing is completely fixed, so the translational and rotational degrees of freedom in the axial and radial directions are restricted; (2) When the inner track of the bearing rotates, it is necessary to restrict the degree of freedom of axial rotation; (3) Because the influence of the cage is ignored when the bearing is modeling, the axial degree of freedom of the rolling element should be limited to ensure that the relative position between the rolling element remains unchanged. After the constraints of each bearing component are set, set the axial preload Fa to 300N on the bearing inner raceway surface, and set the bearing inner raceway speed nm to 10,000 rpm.

As shown in Fig. 6, According to the established finite element model, the ambient temperature is defined as 20 °C, and finally the contact stress analysis of angular contact ball bearing (B7007C) is obtained under the condition of 300 N axial preload Fa and 10,000 rpm rotational speed nm.

Fig. 6
figure 6

Contact stress of each part of bearing

Full size image

Based on the contact stress diagram of the angular contact ball bearing model, it can be seen that the contact stress between the rolling body and the inner and outer orbit contact area is the maximum, and the stress away from the contact area gradually decreases. According to the stress and contact area, calculate the inner and outer orbit contact force. The results are compared with those predicted by the theoretical model that takes into account thermal effects.

3.2 Model Comparison

Based on the comparison between the results obtained from the thermodynamic coupled finite element model and those derived from the theoretical model, as shown in Fig. 7, it can be seen that when the axial preload is 300 N, the contact force of the inner and outer orbit of the angular contact ball bearing keeps the same trend with the temperature rise. The average error of finite element solution of inner normal contact force is 2.7%. The average error of outer normal contact force is 3.9%. The source of error may be due to the size of contact area in finite element calculation, which is greatly affected by meshing. The calculated values of finite element are in good agreement with those of theory. Therefore, the theoretical model and finite element model in this paper have high reliability.

Fig. 7
figure 7

Comparison between theoretical model and finite element model (Fa = 300 N, nm = 10,000 rpm)

Full size image

4 Experimental System

In order to study the influence of temperature rise and speed on dynamic characteristics for ball bearing shaft system, the schematic diagram of bearing test rig is used as shown in Fig. 8, which mainly include shaft-bearing system, drive motor, CNC system, sensor system and temperature control system. The experiment was completed under the condition that the indoor temperature was maintained at about 20 °C in spring. The speed of the motor is controlled by CNC system, and the rated speed of the bearing B7007C is 23,800 rpm, but the spindle does not need to use very high speed conditions in actual work, so the two speeds of 5000 rpm and 10,000 rpm are selected as the research conditions of the test. The heater is seated in the middle of bearing-shaft system and controlled by automatic temperature control system. Before each test, the bearing area of the spindle system is heated with a heater for more than 8 h in advance to ensure that the system reaches thermal balance, and then stiffness and vibration tests are carried out. There are two accelerometer sensors and thermocouple sensors for bearing. The eddy current sensor can be used to measure shaft displacement and the PCB force hammer is used to produce a force for shaft. The test procedure is as follow:

Fig. 8
figure 8

Experimental system

Full size image

The relation of shaft-bearing system’s temperature-stiffness: when the spindle system is at rest, PCB modal impact hammer is used to impose an excitation on the spindle end, and the vibration displacement data of the spindle end collected by the displacement sensor and the force signal collected by the force hammer are transmitted to the computer through the controller, the stiffness of the shaft-bearing system can be calculated according to the ratio of the collected force data to the displacement data, and the stiffness data of the shaft-bearing system are analyzed by LabVIEW software;

The relation of shaft-bearing system’s temperature-vibration: when the spindle operates at 5000 rpm and 10,000 rpm, the acceleration sensor and magnetic holder were assembled and placed in the bearing housing. The eddy current displacement sensor was fixed through the magnetic holder bracket and placed at the front end of the spindle. The collected experimental data were stored and displayed in real time through LabVIEW software.

5 Results and Discussion

5.1 The Relation of Shaft-Bearing System’s Temperature-Stiffness

For different temperature rise, the normal contact force Qi(o) rise with the temperature increased. The purpose of this contact load is tuned to the stiffness, the actual relation temperature-stiffness was demonstrated directly by force hammer and eddy current sensor. The stiffness with different temperature rise, is presented in Fig. 9. According to the experimental data, the finding is as follow:

Fig. 9
figure 9

The relation of temperature and stiffness

Full size image

Bearing temperature has an obvious effect on stiffness for shaft-bearing system; The stiffness of shaft-bearing system increased gradually with the increase of temperature rise; From test data, the shaft-bearing system stiffness increases linearly with temperature rise and the change rate ups to 0.2 × 105 N/m °C ; When the bearing temperature increases by 40 °C, the shaft-bearing system stiffness increases by 12%.

5.2 The Relation of Shaft-Bearing System’s Temperature-Vibration

Considering the influence of temperature rise on rotating system, the vibration characteristics of rotor were changed by controlling the temperature rise of bearing. As shown in Fig. 10, the vibration of shaft-bearing system under different speed (5000 rpm and 10,000 rpm) and temperature rise (20 °C and 40 °C). From test data, the vibration of shaft at 10,000 rpm is significantly stronger than at 5000 rpm. When the bearing temperature rise from 20 to 40 °C, the root-mean-square value of shaft vibration is reduced by 61.2% at 10,000 rpm and by 65.1% at 5000 rpm, the peak-to-peak value of shaft vibration is reduced by 60% at 10,000 rpm and by 63.1% at 5000 rpm.

Fig. 10
figure 10

The relation of temperature-vibration with different speed

Full size image

It can be found from the test that the rotor vibration can be effectively controlled by changing the bearing temperature. In the machining process, the bearing contact load between the rolling and the raceway can be obtained according to the bearing dynamic model, and the bearing temperature can be precisely controlled according to the working conditions. This phenomenon has not shown this good vibration elimination in previous literature.

6 Conclusions

The paper proposes a real-time method to control bearing system dynamics by using temperature to influence vibration. Considering bearing thermal expansion, we studied the effects of temperature on contact angle, load, and stiffness between ball and raceway. The thermodynamic coupling finite element model of bearing based on ANSYS Workbench is compared with the theoretical model proposed, and the result verifies its accuracy. The following conclusions can be obtained:

  • The temperature rise has a significant effect on the dynamic characteristics of the bearing, changing the contact angle between the bearing ball and the inner/outer ring, as well as affecting the contact load and bearing stiffness. The simulation data show that with the increase of temperature, the contact angle between inner ring and outer ring decreases, while the contact load and bearing stiffness increase. For example, when the bearing speed is 5000 rpm and the temperature rise increases by 40° C, the contact angle of the inner ring and the outer ring decreases by 0.8° and 0.7° respectively, and the contact load of the inner ring and the outer ring increases by 5.2% and 5.1% respectively. At the same time, bearing stiffness increased by 4.3%.

  • The thermodynamic coupling finite element model was established and compared with the theoretical model. It was observed that with increasing temperature, the contact force between the ball and both the inner and outer raceway of the bearing demonstrated a consistent trend. The proposed model in this paper is validated with an average discrepancy of 2.7% and 3.9% for inner ring contact force and outer ring contact force, respectively, between the finite element solution and theoretical value.

  • An experimental platform was established to investigate how temperature affects bearing system stiffness and vibration. The test data showed that the stiffness increased linearly with the temperature rise, and the change rate reached 0.2 × 105 N/m °C. Specifically, when the bearing temperature rose by 40 °C, its stiffness increased by 12%. Moreover, elevating the bearing temperature from 20 to 40 °C results in a reduction of rotor vibration peaks by 60% at 10,000 rpm and by 63.1% at 5000 rpm. Temperature elevation effectively enhances bearing system stiffness and mitigates vibration, providing a real-time temperature control approach for managing rotor system vibrations in engineering applications.