Development of Automatic Chatter Suppression System in Parallel Milling by Real-Time Spindle Speed Control with Observer-Based Chatter Monitoring

Abstract

To maximize the potential for high material removal rates in simultaneous processes such as parallel milling, developing strategies for successful chatter suppression/avoidance is an important concern for manufacturers. In this study, the effectiveness of the spindle speed difference method (SDM) for chatter suppression is discussed in a parallel end-milling process where a flexible workpiece is machined by two tools rotating in opposite direction. The process model is developed, considering that the dynamic variation due to the regenerative effect occurs on a plane perpendicular to the tool axis direction. Through the process simulations and the experiments, this study provides informative discussion for comprehending the process behavior. Additionally, a real-time active chatter suppression system with adaptive SDM, where the spindle speed difference is sequentially optimized during the process according to the tracked chatter frequency, is developed by integrating a chatter monitoring system based on sensorless cutting force estimation with sliding discrete Fourier transform. The results show that the developed real-time adaptive system of spindle speed suppresses chatter vibrations more effectively than non-adaptive SDM system; hence, the integrated system can contribute self-optimizing machining systems oriented to Industry 4.0.

1 Introduction

Multitasking machines such as mill turn centers can realize highly efficient part manufacturing and shortened production cycles by increasing the material removal rate (MRR) using multiple tools and/or aggregating processes [1, 2]. However, simultaneous machining processes are often accompanied by severe chatter problems because of the complex process–machine interaction in the cutter–workpiece system (CWS); therefore, setting the appropriate cutting conditions become significantly more important, compared with that in conventional machining processes.

For a stable process planning, stability analysis represented by stability lobe diagrams (SLDs) has been studied in parallel turning [3,4,5,6], parallel milling [7, 8], and the turn-milling processes [9, 10]. This research direction is essential to comprehend the phenomenon and the behavior of process stability. For instance, Brecher et al. [7] showed that the relative angular tool offset (ATO) between multiple milling tools, which yields phase differences of cutting forces at each CWS, significantly affects the stability if the same spindle speed is applied to all tools. In this case, the combination of cutting type (e.g., up or down cut), in addition to the ATO, greatly alters the process stability [8]. Budak et al. [8] demonstrated that the stability margin of parallel milling with a flexible workpiece can be increased substantially by optimally tuning the spindle speeds of both tools.

However, the SLD approach requires time-consuming preliminary tests to accurately identify the dynamics and process parameters of CWSs. This drawback becomes increasingly evident especially in complex simultaneous processes because many process and dynamics parameters must be considered. In addition, SLDs are sensitive to variations in the dynamics and excited mode shapes, depending on the cutting points and material removal, particularly in the case of a flexible workpiece [8, 11,12,13]. Ensuring reliable stability prediction (particularly for simultaneous machining processes) is challenging; thus, self-active chatter suppression/avoidance with a simple setup is extremely important as another research and development direction for dual safety systems [14, 15].

Establishing control strategies for the spindle speed, such as discrete spindle speed tuning (DSST) [16] and continuous spindle speed variation (CSSV) [17] is useful, because they can be fully implemented only with the spindle system. DSST and CSSV are widely recognized as effective and flexible chatter mitigation techniques in conventional machining processes. In terms of parallel milling, only Shamoto et al. [11, 12] proposed a simple strategy in which the chatter (i.e., regenerative effect) is canceled out comprehensively by a plurality of cutters rotating at different speeds, which is termed as the speed difference method (SDM). In the SDM, the optimal speed difference is provided only from the chatter frequency. They presented the SDM for a flexible thin plate machined by double-side face milling rotating in the same direction, where a single degree-of-freedom (DOF) vibration in a one-dimensional space perpendicular to the machining surface (i.e., thickness direction of the workpiece) can be assumed. Considering only regenerative effect in the thickness direction, they clarified the effectiveness of the SDM analytically and experimentally.

If there are flexibilities on a plane perpendicular to the tool axis direction, however, two tools should be rotated in the opposite direction to balance the cutting forces. In addition, dynamic variations of the cutting width will dominantly occur on this plane, which must be considered.

As the first purpose of this study, the SDM for a flexible workpiece simultaneously machined by two tools rotating in the opposite direction is analyzed focusing the regenerative effect on a plane perpendicular to the tool axis direction. The process models of our experimental environment were developed in Sect. 3. Because the effectiveness of SDM has not been elucidated for this scenario, it is discussed in Sect. 4 with a series of developed process simulations in the time and frequency domains. It was also confirmed experimentally in Sect. 5.

Furthermore, an automatic chatter suppression system was developed based on the findings obtained in this paper. This is second purpose of this study for self-optimizing machining systems (SOMS) [18] oriented to Industry 4.0. To suppress the chatter vibration more robustly, the difference of spindle speeds was adaptively optimized during the process (i.e., adaptive SDM) according to the chatter frequency tracked from the cutting force estimated by a sensorless cutting force observer. The developed real-time adaptive SDM system and its effectiveness are also presented in Sect. 5, followed by the conclusion in Sect. 6.

2 Experimental Environment

The experimental system and the assumptions made in this study are described in this section.

2.1 Realization of Parallel End-Milling Process

Figure 1 shows a multitasking machine tool (Super NTY3, Nakamura-Tome Precision Industry Co., Ltd.). The machine tool is modified such that it can be flexibly controlled by an industrial motion controller (Power PMAC, OMRON Corporation). A slender cylindrical workpiece chucked on a left-side work spindle is machined from both sides using the upper tool (tool 1) and lower tool (tool 2) simultaneously. In this study, the cutting conditions except the spindle speed are set to be the same at both sides. The tool positions of the two tools along the Z-direction were identical; thus, the feed speed was fixed even if the spindle speed of either tool changed. Note that the tools rotate in the opposite direction when viewed from the same direction to balance the cutting forces in both X- and Y-directions. The specifications of the experimental systems are summarized in Table 1.

Fig. 1

Parallel end milling process with multitasking machine tool a machine configuration, b schematic figure of experiment

Table 1 Specifications of experimental system and conditions

A series of stable single slotting tests with an SUS303 plate and a similar tool shown in Table 1 were performed on a three-axis milling center to identify the specific cutting forces and edge-force coefficients using the average cutting force method [19]. The identified values are listed in Table 2.

Table 2 Summary of identified parameters

In addition, preliminary tap tests were performed to comprehend the dynamic behavior of the experimental system. Figure 2 shows the direct frequency response functions (FRFs) of the workpiece in the Y-direction and those of tool 2 in the Y- and Z-directions because the regenerative effect on ZY-plane is focused. The dominant local modes of tool 2 were observed at approximately 2000 Hz, which is significantly higher than the resonance of the workpiece. Moreover, the corresponding compliance gain of tool 2 was significantly smaller than that of the workpiece. The peak compliance gain of tool 1 did not differ significantly from that of tool 2. Consequently, regenerative chatter should be predominantly induced by the dynamics of the flexible workpiece; hence, only the workpiece dynamics is considered for a clear discussion in the simulation section. Note that, because of the slender cylindrical workpiece, X-direction of the workpiece is also flexible, which can cause the chatter as referenced in [11, 12]. However, the regenerative gain (i.e., the dynamic variation of cutting width and resultant dynamic cutting forces) is significantly smaller than that in Y-direction. Therefore, the vibration on ZY-plane (especially in Y-direction) will become the dominant factor of chatter onset.

Fig. 2

Measured FRFs of tool 2 and workpiece

The modal parameters of the workpiece identified in the YZ-direction are shown in Table 2, although the compliance of cross FRFs ($G_{zy}^{\text{w}}$ and $G_{yz}^{\text{w}}$) and direct FRF in the Z-direction ($G_{zz}^{\text{w}}$) are small compared with $G_{yy}^{\text{w}}$ (Fig. 3). The fitting result of $G_{yy}^{\text{w}}$ is depicted in Fig. 2 as well. Only the higher compliance mode of $G_{yy}^{\text{w}}$ is considered, although multiple vibration modes can be considered in the simulation. Based on another experiment for modal analysis, it was identified that the higher mode at ~ 641 Hz is the local first bending mode of the slender workpiece.

Fig. 3

Gain characteristic of modeled FRFs of workpiece

2.2 Implementation of Sensorless Cutting Force Estimation

An optical linear encoder (LC415, Heidenhain) was attached only to the XY-axis of the upper turret driven by a ball-screw system. This enables the construction of a multiencoder-based disturbance observer (MEDOB) for the cutting force estimation [20]. The equation for estimating the cutting force in MEDOB was derived by correlating the motor- and load-side motion equations of the dual-inertia model of the ball-screw-driven stage as follows:

$$\hat{F}_{cut} = G_{LPF} \left( {\frac{{K_{tn} }}{{R_{n} }}I_{a}^{ref} - \frac{{J_{rn} }}{{R_{n} }}\hat{\alpha }_{r} - M_{tn} \hat{a}_{t} - \hat{F}_{stat} } \right)$$

(1)

The motor angular acceleration, $\alpha_{r} \,[{\text{rad}}/{\text{s}}^{2} ]$, and stage acceleration, $a_{t} \,[{\text{m}}/{\text{s}}^{2} ]$, are estimated from the attached rotary and linear encoders, respectively. Also, the motor current reference, $I_{a}^{ref} \,[{\text{A}}]$, can be obtained as servo information. In this study, nominal model parameters were defined from machine specifications. In addition, the non-process-related static force, $F_{stat} \,[{\text{N}}]$, including friction and gravity terms were preliminarily identified to be subtracted in the estimation (Table 2). By integrating the linear encoder information that is closer to the cutting point, MEDOB can maintain a high sensitivity against the high-frequency process force [21]. In particular, it was confirmed that the X-axis of the upper turret can capture the vibration state more sensitively because of the low-damping rolling guideway; thus, the cutting force estimated in the X-axis of the upper turret was employed for chatter monitoring. A low-pass filter (LPF) was applied to eliminate high-frequency noise, and the estimated cutting force was then recorded at every 333 μs (3 kHz).

3 Modeling of Double-Sided Parallel End-Milling Process

3.1 Time-Domain Modeling

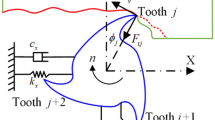
Figure 4 shows a schematic of the double-side parallel end-milling process. The local Cartesian coordinate system xyz and rotating coordinate uv are defined in each tool. The workpiece coordinate system $x^{\text{w}} y^{\text{w}} z^{\text{w}}$ coincides with the global coordinate system of the machine shown in Fig. 1. In the time-domain simulation, the minute cutting forces are calculated in the discrete minute disk elements divided along the tool axial direction as Δa_p = a_p/L. Subsequently, the total cutting force is derived by summing the directional minute cutting forces. Assuming that each minute cutting force acts on the corresponding cutting edge, the minute cutting forces in the tangential, radial, and axial directions at the tooth $j \left( {j = 1,2, \ldots ,Z^{{{\text{t}}l}} } \right)$ in the disk $m \left( {m = 1, 2, \ldots , L^{tl} } \right)$ of tool $l \left( {l = 1,2} \right)$ can be calculated as follows:

Fig. 4

Schematic figure of double-side parallel end-milling process

$$\begin{aligned} & dF_{tj,m}^{{{\text{t}}l}} \left( {\theta_{j, m}^{{{\text{t}}l}} } \right) = \left[ {K_{tc}^{{{\text{t}}l}} h_{j}^{{{\text{t}}l}} \left( {\theta_{j,m}^{{{\text{t}}l}} } \right) + K_{te}^{{{\text{t}}l}} } \right]g\left( {\theta_{j,m}^{{{\text{t}}l}} } \right)\Delta a_{p}^{{{\text{t}}l}} \\ & dF_{rj,m}^{{{\text{t}}l}} \left( {\theta_{j, m}^{{{\text{t}}l}} } \right) = \left[ {K_{rc}^{{{\text{t}}l}} h_{j}^{{{\text{t}}l}} \left( {\theta_{j,m}^{{{\text{t}}l}} } \right) + K_{re}^{{{\text{t}}l}} } \right]g\left( {\theta_{j,m}^{{{\text{t}}l}} } \right)\Delta a_{p}^{{{\text{t}}l}} \\ & dF_{a j, m}^{{{\text{t}}l}} \left( {\theta_{j,m}^{{{\text{t}}l}} } \right) = \left[ {K_{ac}^{{{\text{t}}l}} h_{j}^{{{\text{t}}l}} \left( {\theta_{j,m}^{{{\text{t}}l}} } \right) + K_{ae}^{{{\text{t}}l}} } \right]g\left( {\theta_{j,m}^{{{\text{t}}l}} } \right)\Delta a_{p}^{{{\text{t}}l}} \\ \end{aligned}$$

(2)

where $\theta_{j, m}^{{{\text{t}}l}} \,[{\text{rad}}]$ is the corresponding rotating angle of cutting edge, which also depends on the pitch and helix angle of tool, and $g\left( {\theta_{j,m}^{{{\text{t}}l}} } \right)$ is unit step function to discriminate whether the tooth is in or out of cut.

Basically, the engagement angle can be calculated based on the relationship between the tool diameter and the radial depth of cut. When a cylindrical workpiece is machined, the start and exit angle for engagement also depend on the height in the tool axis direction; hence the engagement angle must be modified at each minute disk element. In this study, however, the engagement angle at the bottom minute disk is used consistently as representative value in all disks, similar to block milling. This assumption is sufficient to capture the process stability behavior.

Here, the uncut chip thickness, $h_{j}^{{{\text{t}}1}} \left( {\theta_{j,m}^{{{\text{t}}1}} } \right)$ and $h_{j}^{{{\text{t}}2}} \left( {\theta_{j,m}^{{{\text{t}}2}} } \right)$, can be derived by considering the dynamic vibration of the CWS as follows:

$$\begin{aligned} & h_{j}^{{{\text{t}}1}} \left( {\theta_{j,m}^{{{\text{t}}1}} } \right) = c_{f}^{{{\text{t}}1}} \sin \theta_{j,m}^{{{\text{t}}1}} + \Delta z^{{{\text{w}},{\text{t}}1}} \sin \theta_{j,m}^{{{\text{t}}1}} - \Delta y^{{{\text{w}},{\text{t}}1}} \cos \theta_{j,m}^{{{\text{t}}1}} \\ & h_{j}^{{{\text{t}}2}} \left( {\theta_{j,m}^{{{\text{t}}2}} } \right) = c_{f}^{{{\text{t}}2}} { \sin }\theta_{j,m}^{{{\text{t}}2}} + \Delta z^{{{\text{w}}, {\text{t}}2}} \sin \theta_{j,m}^{{{\text{t}}2}} + \Delta y^{{{\text{w}},{\text{t}}2}} \cos \theta_{j,m}^{{{\text{t}}2}} \\ \end{aligned}$$

(3)

where

$$\Delta q^{{{\text{w}},{\text{t}}l}} = q^{\text{w}} \left( t \right) - q^{\text{w}} \left( {t - \tau^{{{\text{t}}l}} } \right), q:y, z$$

(4)

Note that tool vibrations are neglected in Eq. (3) because of rigid-tool assumption, although they can be easily considered.

Next, the minute cutting force in Eq. (2) can be converted to the cutting force in the Cartesian tool coordinate system as follows:

$$\begin{aligned} & dF_{xj,m}^{{{\text{t}}l}} \left( {\theta_{j,m}^{{{\text{t}}l}} } \right) = - dF_{aj,m}^{{{\text{t}}l}} \\ & dF_{yj,m}^{{{\text{t}}l}} \left( {\theta_{j,m}^{{{\text{t}}l}} } \right) = + dF_{tj,m}^{{{\text{t}}l}} \sin \theta_{j,m}^{{{\text{t}}l}} - dF_{rj,m}^{{{\text{t}}l}} \cos \theta_{j,m}^{{{\text{t}}l}} \\ & dF_{zj,m}^{{{\text{t}}l}} \left( {\theta_{j,m}^{{{\text{t}}l}} } \right) = - dF_{tj,m}^{{{\text{t}}l}} \cos \theta_{j,m}^{{{\text{t}}l}} - dF_{rj,m}^{{{\text{t}}l}} \sin \theta_{j,m}^{{{\text{t}}l}} \\ \end{aligned}$$

(5)

Subsequently, the total cutting forces of the l-th tool in the xyz-direction are obtained by summing Eq. (5):

$$F_{q}^{tl} \left( {\theta^{tl} } \right) = \mathop \sum \limits_{j = 1}^{{Z^{tl} }} \mathop \sum \limits_{m = 1}^{{L^{tl} }} dF_{qj,m}^{tl} \left( {\theta_{j,m}^{tl} } \right), q: x, y, z$$

(6)

Finally, the cutting forces acting on the workpiece are defined based on the directional cutting forces of each tool by considering the law of action and reaction, as follows:

$$\begin{aligned} & F_{x}^{\text{w}} \left( {\theta^{{{\text{t}}1}} , \theta^{{{\text{t}}2}} } \right) = + F_{x}^{{{\text{t}}1}} \left( {\theta^{{{\text{t}}1}} } \right) - F_{x}^{{{\text{t}}2}} \left( {\theta^{{{\text{t}}2}} } \right) \\ & F_{y}^{\text{w}} \left( {\theta^{{{\text{t}}1}} , \theta^{{{\text{t}}2}} } \right) = - F_{y}^{{{\text{t}}1}} \left( {\theta^{{{\text{t}}1}} } \right) + F_{y}^{{{\text{t}}2}} \left( {\theta^{{{\text{t}}2}} } \right) \\ & F_{z}^{\text{w}} \left( {\theta^{{{\text{t}}1}} , \theta^{{{\text{t}}2}} } \right) = + F_{z}^{{{\text{t}}1}} \left( {\theta^{{{\text{t}}1}} } \right) + F_{z}^{{{\text{t}}2}} \left( {\theta^{{{\text{t}}2}} } \right) \\ \end{aligned}$$

(7)

A time-domain chatter simulation can be performed using the coupled calculation of the cutting force and the vibration responses of the workpiece based on the equations above and the modeled FRFs.

3.2 Frequency Domain Modeling

In this subsection, the frequency-domain model is described to discuss the stability behavior. Figure 5 shows the block diagram representing the dynamic variation of the double-side parallel end-milling process in the ZY-plane, assuming rigid tools and a flexible workpiece. Note that, in Fig. 5, the same cutting conditions with identical tools are assumed on both sides, except the spindle speed. Additionally, zeroth order approximation (ZOA) [22] is introduced. Consequently, the characteristic force equation in Fig. 5 can be obtained as follows:

Fig. 5

Block diagram of double-side parallel end-milling process in case of rigid tools and a flexible workpiece

$$\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} = \frac{1}{2}a_{p} K_{tc} \left\{ {\left[ {\begin{array}{*{20}c} {2\alpha_{0 zz} } & 0 \\ 0 & {2\alpha_{0 yy} } \\ \end{array} } \right] - e^{{ - i\varepsilon^{t1} }} \left[ {\begin{array}{*{20}c} {\alpha_{0 zz} } & { - \alpha_{0 zy} } \\ { - \alpha_{0 yz} } & {\alpha_{0 yy} } \\ \end{array} } \right] - e^{{ - i\varepsilon^{t2} }} \left[ {\begin{array}{*{20}c} {\alpha_{0 zz} } & {\alpha_{0 zy} } \\ {\alpha_{0 yz} } & {\alpha_{0 yy} } \\ \end{array} } \right]} \right\}\left[ {\begin{array}{*{20}c} {G_{zz}^{w} } & {G_{zy}^{w} } \\ {G_{yz}^{w} } & {G_{yy}^{w} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\}$$

(8)

where the time-invariant average directional dynamic milling force coefficients, α₀, can be defined in the same way as conventional single milling process in [22].

Here, the phase difference between tools 1 and 2, $\Delta \varepsilon \,[{\text{rad}}]$ can controlled by changing the spindle speed, and the phase shift between the previous and present vibration at tool 2, $\varepsilon^{{{\text{t}}2}} \,[{\text{rad}}]$ can be expressed as follows:

$$\varepsilon^{t2} = \varepsilon^{t1} + \Delta \varepsilon \to e^{{ - i\varepsilon^{t2} }} = e^{ - i\Delta \varepsilon } e^{{ - i\varepsilon^{t1} }}$$

(9)

As a result, Eq. (8) can be rearranged as follows:

$$\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} = \frac{1}{2}a_{p} K_{tc} \left\{ {\left[ {A_{0} } \right] - e^{{ - i\varepsilon^{t1} }} \left[ {DM_{\Delta } } \right]} \right\}\left[ {TF} \right]\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\}$$

(10)

where

$$\left[ {A_{0} } \right] = \left[ {\begin{array}{*{20}c} {2\alpha_{0zz} } & 0 \\ 0 & {2\alpha_{0yy} } \\ \end{array} } \right]$$

(11)

$$\left[ {DM_{\Delta } } \right] = \left[ {\begin{array}{*{20}c} {\left( { + 1 + e^{ - i\Delta \varepsilon } } \right)\alpha_{0 zz} } & {\left( { - 1 + e^{ - i\Delta \varepsilon } } \right)\alpha_{0 zy} } \\ {\left( { - 1 + e^{ - i\Delta \varepsilon } } \right)\alpha_{0 yz} } & {\left( { + 1 + e^{ - i\Delta \varepsilon } } \right)\alpha_{0 yy} } \\ \end{array} } \right]$$

(12)

$$\left[ {TF} \right] = \left[ {\begin{array}{*{20}c} {G_{zz}^{w} } & {G_{zy}^{w} } \\ {G_{yz}^{w} } & {G_{yy}^{w} } \\ \end{array} } \right]$$

(13)

By numerically searching the critical value of axial depth of cut, which satisfy with Eq. (10), while varying the chatter frequency, SLDs can be obtained (see “Appendix”).

4 Selection of Appropriate Spindle Speed Through Simulation

In [11, 12], the SDM for chatter suppression was used in the double-side face milling of flexible thin plates. In this case, the delay term of the total CWS at the workpiece is simply expressed as $e^{{ - i\varepsilon^{{{\text{t}}1}} }} + e^{{ - i\varepsilon^{{{\text{t}}2}} }}$, if the regenerative widths are almost the same at both sides. Subsequently, by setting Δɛ as

$$\Delta \varepsilon = \pi \left( {2n + 1} \right)\quad {\text{where}}\quad n = 0,1,2, \ldots ,$$

(14)

the total delay term becomes ideally zero (i.e., the regenerative effect diminishes) as follows:

$$e^{{ - i\varepsilon^{t1} }} + e^{{ - i\varepsilon^{t2} }} \to e^{{ - i\varepsilon^{t1} }} \left( {1 + e^{{ - i\left( {\pi + 2\pi n} \right)}} } \right) = 0$$

(15)

Here, Eq. (14) is equivalent to setting the difference of the tooth-pass period, $\Delta T_{z} \left( { = T_{z}^{{{\text{t}}2}} - T_{z}^{{{\text{t}}1}} } \right) \left[ {\text{s}} \right]$, between the two tools as follows:

$$\omega_{c} \Delta T_{z} = \Delta \varepsilon \to \Delta T_{z} = \frac{\Delta \varepsilon }{{\omega_{c} }} = \left( {\frac{1}{2} + n} \right)T_{c}$$

(16)

where is $\omega_{c} \,[{\text{rad/s}}]$ a chatter frequency, and $T_{c} \,[{\text{s}}]$ is the corresponding chatter vibration period (i.e., $T_{c} = 2\pi /\omega_{c}$).

This is the principle of the SDM for chatter suppression in parallel milling. However, the effectiveness of SDM has not been elucidated in the process model of Fig. 5. Therefore, it is discussed in this section through both frequency-domain stability analysis and time-domain process simulation. In the simulations, the cutting conditions, such as the tool geometries, feed speed, and radial depth of cut, were unified to the experimental ones shown in Table 1. In addition, the force coefficients and machine dynamics listed in Table 2 were used for the simulation.

4.1 Stability Analysis in Frequency Domain

Figure 6 shows the SLD of the conventional and parallel milling for the same spindle speed on both sides. In this case, the asymptotic axial depth in each tool ($a_{p}^{t1} = a_{p}^{t2}$) was 0.23 mm for parallel milling with the same spindle speed, whereas a more-than-twice asymptotic borderline of 0.64 mm was predicted for conventional milling. This shows that parallel milling more significantly affects the regenerative effect compared with the conventional process, and the total MRR cannot be increased in this case. However, the process stability can be enhanced by providing an appropriate phase difference by controlling the spindle speed.

Fig. 6

SLDs of conventional and parallel milling with the same spindle speed at both sides

Figure 7 shows the SLDs in some phase differences. The stability limit increases if phase differences are applied, and the maximum stability with $\Delta \varepsilon = \pi$ is observed, similar to a previous study [11, 12]. This is because the dominant flexibility exists only in the Y-direction where process can be regarded as 1DOF system. Based on Eq. (12), the diagonal terms of delay matrix can be cancelled out. However, nondiagonal terms remained, as the average directional force coefficients in the simulated conditions were $\alpha_{0zz} = - 0.393$, $\alpha_{0zy} = - 1.00$, $\alpha_{0yz} = 1.00$, and $\alpha_{0yy} = - 0.393$, respectively. To sum up, it is inherently impossible to completely cancel out the regenerative effect unlike the previous study. Due to the nondiagonal terms, the regenerative effect in the Y-direction is transferred to the Z-direction, and vice versa. Since the workpiece in the Z-direction was rigid, the stability was improved in this case.

Fig. 7

SLDs with phase shift difference in parallel milling

Generally, the mode coupling chatter is inevitable even in the SDM. Especially, in case of Fig. 5, the remaining nondiagonal terms may encourage the mode coupling effect. Figure 8 shows the SLDs in cases of symmetric dynamics under slotting and quarter-immersion down cutting. Other process conditions are the same. In the slotting case of Fig. 8, the phase difference of Δɛ = π decreases the process stability because the nondiagonal terms of delay matrix that is amplified by SDM produce the large mode coupling effect. A simple method to eliminate mode coupling is to regulate the radial depth of cut [23]. For instance, the stability improvement with Δɛ = π were observed in the quarter immersion down cutting where α_0zz = 0.162, α_0zy = - 0.377, α_0yz = 0.289, and α_0yy = - 0.424. Therefore, the SDM should be carefully applied if the process has 2DOF system with a mode coupling effect.

Fig. 8

SLDs of parallel milling process (slotting and quarter immersion down cutting) with symmetric dynamics ($G_{zz}^{\text{w}} = G_{yy}^{\text{w}}$)

4.2 Time-Domain Process Simulation

Figure 9 shows the simulation results of parallel milling using the same spindle speed of 960 min⁻¹ (i.e., Δɛ = 0). In the time-domain simulation, the vibration responses were calculated by solving the modeled differential equation at each sampling (10 kHz) using the fourth-order Runge–Kutta method. The nonlinearity [24] such as jumping effect of CWS was considered (i.e., the cutting forces become zero when the negative uncut chip thickness is calculated), whereas the multiple regenerative effect was not considered. Additionally, the forced vibration components yielded by the tooth-pass and its harmonic cutting forces were eliminated by using the comb filter [25], and then only chatter components were displayed.

Fig. 9

a Simulated parallel milling with the same spindle speed ($S^{t1} = S^{t2} = 960\,\min^{ - 1} , a_{p} = 0.4\,{\text{mm}}$), and b its fast Fourier transform (FFT)

In Fig. 9, chatter vibration was clearly observed, as predicted in Fig. 7. Note that the ATO was set to zero so that the chatter would not ideally occur, because the cutting force in the Y-direction was completely canceled out at both sides. However, the cross FRFs began to destabilize the process because the cutting force in the Z-direction could not be canceled simultaneously. Once a slight vibration occurred in the Y-direction, the process was significantly affected by the regenerative effect. It is noteworthy that multiple vibration frequencies were excited even in the slotting test with one dominant mode considered. These frequencies neighbored the resonant frequency, and the frequency spacing was 32 Hz, corresponding to the tooth-pass frequency. This indicates that the ZOA, which assumes the single dominant chatter frequency, may not be suitable for accurately analyzing SLDs, although the process stability tendency may be captured. The maximum frequency spectrum component was regarded as the chatter frequency, i.e., 659.2 Hz.

Figure 10 shows the results of applying SDM to Fig. 9 with $\Delta \varepsilon = \pi /2 \left( {S^{t1} = 972\,\min^{ - 1} } \right)$, $\Delta \varepsilon = \pi \left( {S^{t1} = 984\,\min^{ - 1} } \right)$, and $\Delta \varepsilon = 5\pi /4 \left( {S^{t1} = 990\,\min^{ - 1} } \right)$. The ATO did not affect the process in cases involving different spindle speeds, because the rotational angle between the tools varied continuously [8]. As shown in Fig. 10, chatter was attenuated in all the results, and the most effective chatter suppression occurred at Δɛ = π. These results are consistent with the stability behavior shown in Fig. 7.

Fig. 10

Time waveform and its FFT result of the simulated parallel milling with speed difference ($S^{t2} = 960\,\min^{ - 1} , a_{p} = 0.4\,{\text{mm}}$): a $\Delta \varepsilon = \pi /2$ ($S^{t1} = 972\,\min^{ - 1}$), b $\Delta \varepsilon = \pi$ ($S^{t1} = 984\,\min^{ - 1}$), c $\Delta \varepsilon = 5\pi /4$ ($S^{t1} = 990\,\min^{ - 1}$)

However, it is noteworthy that the vibration increased and decreased periodically depending on the difference in tooth-pass frequency between the two tools. A similar nonlinear beat vibration was observed in the spindle speed variation process, and it could not be analyzed by frequency-domain stability analysis [26]. Consequently, the beat vibration complicated the process stability interpretation. For instance, the vibration level was sufficiently low at some time points in $\Delta \varepsilon = 5\pi /4$, because the depth of cut was below the corresponding stability limit in Fig. 7. However, the vibration was amplified at other time points. This beat vibration will pose a problem if the SDM is applied in the parallel end milling process; therefore, it should be avoided to the maximum possible extent. In the high lobe number zone (e.g., ${\text{floor}}\left( {\omega_{c} T_{z} /\left( {2\pi } \right)} \right) = 20$ in Fig. 9), the beat vibration changed sensitively with a slight difference in the spindle speed (e.g., only a 6 min⁻¹ difference between Fig. 10b, c). Therefore, it is crucial to select the spindle speed based on the accurate tracking of the chatter frequency in actual conditions during process.

5 Experimental Verification with Observer-Based Chatter Monitoring

The effectiveness of the SDM in parallel end-milling is verified in this section based on the experiments performed. In addition, an automatic chatter suppression system with adaptive spindle speed control based on observer-based chatter monitoring was developed. The experimental setup and the conditions are detailed in Table 1.

5.1 Offline Analysis of Spindle Speed Section

Figure 11 shows the experimental results for the same spindle speed on both sides (i.e., $S^{t1} = S^{t2} = 960\,\min^{ - 1}$). The cutting force was overestimated, particularly in the high-frequency region, owing to modeling errors and numerical differential. Nevertheless, the estimated cutting force sensitively reflected the vibrational state, including the high-frequency chatter and low-frequency forced vibration components (Fig. 11b). As discussed in the previous section, multiple chatter frequencies were clearly observed in the tooth-pass frequency interval (i.e., 32 Hz). In fact, chatter marks and consequently a deteriorated surface roughness of 8.22 μm (measured using Surfcom Flex-50A form Tokyo Seimitsu Co., Ltd) were observed (Fig. 11c). The maximum spectrum frequency of 984 Hz was regarded as the chatter frequency.

Fig. 11

Experimental results for the same spindle speed. ($S^{t1} = 960\,\min^{ - 1}$ and $S^{t2} = 960\,\min^{ - 1}$): a estimated cutting force, b its FFT, and c appearance of machined surface

Here, the axial depth of cut for chatter onset in the experiment (i.e., 2 mm) was significantly larger than the analyzed stability limit in the previous section. One possible reason is a decrease in the engagement angle along tool axial direction due to the cylindrical workpiece, which is not considered in the simulation. Additionally, the stiffness of the CWS probably increased under actual cutting conditions. Because the double-side slotting test was performed at the same position along the Z-direction, the system was assumed to behave like a double-supported beam. In fact, the measured chatter frequency was significantly higher than the resonant frequency obtained in the tap test under the cantilever-beam state. This indicates the difficulty of accurate process prediction and importance of automatic and adaptive chatter suppression system with tracking the chatter frequency during the actual process conditions.

Based on the chatter frequency of 984 Hz, the SDM was designed using Eq. (16) with n = 1, where the spindle speed of tool 1 was changed (i.e., $S^{t1} = 1009\,\min^{ - 1}$ and $S^{t2} = 960\,\min^{ - 1}$). The results are shown in Fig. 12. The chatter vibration was clearly suppressed, and the surface roughness was reduced to 4.73 μm. However, beat vibration in the time waveform and beating marks on the machine surface were observed, as shown in Fig. 12a, c. There were five beating marks at every 3 mm, corresponding to approximately 1.67 intervals per second considering a feed speed of 60 mm/min. This is approximately the same as the difference between the tooth-pass frequencies of the two tools (i.e.,$\left( {2 \times 49} \right)/60 = 1.63\,{\text{Hz}}$), as also suggested in the simulation.

Fig. 12

Experimental results of speed difference process designed offline ($S^{t1} = 1009\,\min^{ - 1}$ and $S^{t2} = 960\,\min^{ - 1}$): a estimated cutting force, b its FFT, and c appearance of machined surface

5.2 Development of Adaptive Spindle Speed Control System for Automatic Chatter Suppression

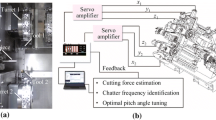
One of the possible reasons for the large beat vibration in the SDM is the variation in the phase difference from the optimal value. Particularly, it changes sensitively in the high-lobe number zone with a slight difference in the spindle speed. In a real system, the chatter frequency may vary according to the cutting position, material removal, and/or slight variation of the experimental setup (e.g., the projection length of the workpiece). Therefore, an automatic chatter suppression system with an adaptive SDM based on in-process monitoring of the chatter state was developed.

To automatically track the chatter frequency in real time during the process, a sliding discrete Fourier transform (SDFT [27]) was applied to the estimated cutting force. In the SDFT, a Fourier transform was conducted at a certain frequency with low computational cost while sliding the window, similar to the moving average [14]. The maximum spectrum component in the high-frequency region was extracted as a chatter frequency. Figure 13 shows the result of in-process chatter frequency extraction from the cutting force estimated from the same-speed parallel milling shown in Fig. 11. The frequency resolution for the SDFT was set to 1 Hz. The spindle speed of tool 1 was altered every 1.0 s, although the chatter frequency was updated every 444 ms.

Fig. 13

Verification of online extraction of chatter frequency by SDFT applied to estimated cutting force

Figure 14 summarizes the results of the adaptive SDM. The spindle control system was switched on from about 10 s, although it could be automatically started using a chatter detection technique (e.g., setting the threshold to the values of the frequency spectra). The experimental results clearly show that the developed system suppressed the chatter vibration by adaptively controlling the spindle speed during the process, based on the chatter frequency that was automatically extracted from the estimated cutting force in real time. Because only the servo information and spindle control system were used for chatter monitoring and suppression, this system required no additional equipment or sensors. Therefore, it would benefit the next-generation machine tools that integrate the SOMS.

Fig. 14

Experimental results of adaptive SDM a extracted chatter frequency, b spindle speed, c estimated cutting force, and d its spectrogram made by short time Fourier transform

Figure 15 shows the moving variance representing the temporal power spectrum of the entire frequency range except for the DC component during each process. In the SDM designed offline, on one hand, the beat vibration according to the difference between the tooth-pass frequencies could be clearly observed, although the chatter was reduced. On the other hand, the adaptive SDM system reduced the chatter vibration more effectively, including the beat vibration, and consequently the surface roughness was reduced to 3.17 μm. This could be because the spindle-speed difference approached the optimal value in the current real condition. The experimental results suggest that the adaptive system is highly promising in achieving a more effective chatter suppression.

Fig. 15

Comparison of moving variance (power spectrum) of the estimated cutting force during each process

Note that the slight beat marks remained even in the adaptive SDM system. However, the SDM is not suitable for finishing processes because of the forced vibration. In finishing processes with a low cutting depth, which is sufficient to avoid the chatter, the forced vibration should be cancelled out by perfectly synchronizing the tool rotation angles and direction on both the sides [28].

6 Conclusion

In this study, the effectiveness of the SDM was discussed in the parallel end-milling process, where dynamic variations due to regenerative effect typically occur on the plane perpendicular to the tool axis direction. The developed process simulation and the experiments were verified. In addition, an automatic chatter suppression system with real-time spindle speed control with chatter monitoring based on sensorless cutting force estimation was developed. The highlights of this study are summarized below.

• 1. The SDM with $\Delta \varepsilon = \pi \left( {2\pi n + 1} \right); n \in {\mathbb{Z}}$ could improve the process stability (i.e., suppress chatter) if the mode coupling effect did not exist. However, in a process with mode-coupling, the SDM might exhibit a contrary effect.

• 2. When the SDM was applied, the beat vibration occurred according to the difference between the tooth-pass frequencies of the two tools, which was also transcribed on the machine surface; hence, it is necessary to avoid the beat vibration to the extent possible. In cases involving large chatter lobe numbers, the beat vibration would be very sensitive to even a slight difference from the optimal value of the spindle speed.

• 3. By using the adaptive SDM system with an observer-based chatter state extraction in real time, the chatter could be suppressed more effectively with less beat vibration. The developed automatic chatter suppression system required no additional equipment or sensors.

Appendix

Equation (10) can be rearranged as follows:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} + \frac{1}{2}a_{p} K_{tc} \left[ {DM_{\Delta } } \right]\left[ {TF} \right]\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} = \frac{1}{2}a_{p} K_{tc} \left\{ {\left[ {A_{0} } \right] - e^{{ - i\varepsilon^{t1} }} \left[ {DM_{\Delta } } \right]} \right\}\left[ {TF} \right]\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} + \frac{1}{2}a_{p} K_{tc} \left[ {DM_{\Delta } } \right]\left[ {TF} \right]\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} \\ & \quad \to \left\{ {\left[ I \right] + \frac{1}{2}a_{p} K_{tc} \left( {\left[ {DM_{\Delta } } \right] - \left[ {A_{0} } \right]} \right)\left[ {TF} \right]} \right\}\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} = \frac{1}{2}a_{p} K_{tc} \left( {1 - e^{{ - i\varepsilon_{1} }} } \right)\left[ {DM_{\Delta } } \right]\left[ {TF} \right]\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} \\ & \quad \to \left\{ {\left[ I \right] + \frac{1}{2}a_{p} K_{tc} \left( {\left[ {DM_{\Delta } } \right] - \left[ {A_{0} } \right]} \right)\left[ {TF} \right]} \right\}\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} = \lambda \left[ {DM_{\Delta } } \right]\left[ {TF} \right]\left\{ {\begin{array}{*{20}c} {F_{z}^{w} } \\ {F_{y}^{w} } \\ \end{array} } \right\} \\ \end{aligned}$$

(17)

By solving the general eigenvalue problem of Eq. (17) and obtaining the eigenvalues, the critical axial depth of cut, a_p(lim) can be derived similarly as in the conventional milling process, as follows:

$$a_{{p\left( {\lim } \right)}} = \frac{{\lambda_{R} }}{{K_{tc} }}\left\{ {1 + \left( {\frac{{\lambda_{I} }}{{\lambda_{R} }}} \right)^{2} } \right\}$$

(18)

The axial depth of cut term is included in the left-hand side of Eq. (17). Therefore, the eigenvalues were searched such that the initially set value of the axial depth of cut was equal to the value calculated using Eq. (18) while updating the initial value.