Ball End Mill—Tool Radius Compensation of Complex NURBS Surfaces for 3-Axis CNC Milling Machines

Abstract

In order to extend the 2D-TRC (tool radius compensation) function of 3-axis CNC milling machines to ball end mills (BEMs), a new TRC named BEM-TRC is proposed to achieve successful milling of complex surfaces without over-cut. The implementation of the BEM-TRC for complex surfaces depicted in NURBS model is divided into three steps. The first one is to search the cutting point (CP) on a NURBS surface using equi-arc length interpolation in u or v direction. The second one is to accomplish BEM-TRC at the CP through offsetting the CP to the cutter center point (CCP) of a BEM along the normal vector at CP. The third one is to compute the cutter location point (CLP) of the BEM according to the BEM-CCP. The simulation and experiment verifies that the BEM-TRC is feasible and effective, and can avoid over-cut phenomenon successfully. The BEM-TRC extends the ability of the traditional 2D-TRC function, and makes 3-axis CNC milling machines to accomplish the milling process of complex NURBS surfaces.

1 Introduction

The non-uniform rational B-splines (NURBS) model provides researchers with an exact uniform representation of analytical shapes as well as free-form parametric curves and surfaces [1,2,3]. Due to the advantages of NURBS, STEP-NC has adopted NURBS as the standard interface for data exchange between CAD/CAM and CNC systems [4, 5]. The NURBS model endows researchers to design a large variety of shapes by operating the control points as well as weights in a flexible way owing to its generality in the expression of complex curves and surfaces [6]. Many CNC system manufacturers devote themselves to developing NURBS interpolators for their CNC systems. Unfortunately, except for few expensive CNC systems, common 3-axis CNC milling machines are equipped with only linear interpolation (G01) and circular interpolation (G02/G03) without NURBS interpolation [7]. How to realize the NURBS interpolation oriented to 3-axis CNC milling machines is still an urgent problem to be solved for such level machines.

Owing to low-cost and flexibility, 3-axis CNC milling machines have been utilized in many industries such as aerospace, ships, die module and automobiles [8]. As a basic and essential function, such level CNC milling machines are equipped with the 2D tool radius compensation (2D-TRC). Except for few CNC systems equipped with 3D-TRC function (such as Mitsubishi CNC 330M/330HM/335M in Japan, Maho CNC432 in Germa ny, etc.), [9,10,11] almost all 3-axis CNC milling machines are equipped with 2D-TRC function which can meet the machining demands for most of planar contours. The 2D-TRC makes the programming procedure to be an easy task for the reason that programmers accomplish programming according to the actual contour of parts without considering the actual tool paths. However, the 2D-TRC function has some disadvantages as follows:

• (1) The 2D-TRC function is only suitable for flat end mills (FEMs), while is unsuitable for ball end mills (BEMs).

• (2) The 2D-TRC function can be only able to cut the planar contours, while be unable to cut complex spatial surfaces.

With the development of machining, complex surfaces have been more and more commonly used in various industries [12,13,14,15]. Such complex surfaces can be machined based on 5-axis CNC milling machines using many CAM software such as UG, CATIA, ProE and PowerMill [16,17,18,19]. However, a lot of companies can’t afford such expensive 5-axis CNC milling machines. Accomplishing the machining of complex surfaces using 3-axis CNC milling machines becomes a practical and cheap choice for many manufacturing enterprises. The CNC milling of complex NURBS surfaces using BEMs has been still a challenge for common 3-axis milling machines equipped with 2D-TRC function and without NURBS interpolation function. In this work, the BEM-TRC of complex NURBS surfaces for 3-axis CNC milling machines is proposed in order to overcome the conundrum. The algorithm, principle and application are discussed in detail. The following goals will be pursued for common 3-axis milling machines: (1) to extend the 2D-TRC function to be applied to BEMs, (2) to explore new TRC method for the milling of NURBS complex surfaces, and (3) to investigate the interpolation method for NURBS complex surfaces with BEM-TRC.

2 NURBS Surface Representation and Its Partial Derivatives

In modern CAD/CAM systems, parts with complex surfaces (e.g. aircraft models, blades, and module dies) are generally expressed in parametric surfaces. In parametric surfaces, NURBS models are becoming more and more important and widely used in the CAD and CAM communities because they offer an exact uniform representation of both analytical and free-form parametric curves and surfaces. As a result, complex surfaces are described by the NURBS model in this work.

A NURBS surface is a bivariate vector-valued piecewise rational function. A p × q degree NURBS surface can be expressed as follows [20]:

$${\varvec{S}}(u,v) = \frac{{\sum\nolimits_{i = 0}^{n} {\sum\nolimits_{j = 0}^{m} {N_{i,p} (u)N_{j,q} (v)w_{i,j} {\varvec{P}}_{i,j} } } }}{{\sum\nolimits_{i = 0}^{n} {\sum\nolimits_{j = 0}^{m} {N_{i,p} (u)N_{j,q} (v)w_{i,j} } } }}\quad (0 \le u,v \le 1)$$

(1)

where {P_i,j} form a bidirectional control point net, {w_i,j} are the weights, and {N_i,p(u)} and {N_j,q(u)} are called pth and qth degree basis functions, respectively. With {N_i,p(u)} as an example, its recursive formulae is written as:

$$\left\{ {\begin{array}{*{20}l} {N_{{i,{0}}} {(}u{)} = \left\{ {\begin{array}{*{20}c} {1} & {\begin{array}{*{20}c} {for} & {u_{i} \le u < u_{{i + {1}}} } \\ \end{array} } \\ {0} & {{\text{otherwise}}} \\ \end{array} } \right.} \hfill \\ {N_{{{\text{i}} ,p}} {(}u{)} = \frac{{u - u_{i} }}{{u_{{{\text{i}} + p}} - u_{i} }}N_{{{\text{i}} ,p - {1}}} {(}u{)} + \frac{{u_{{i{ + }{\text{p}} { + 1}}} - u}}{{u_{{{\text{i}} + p + {1}}} - u_{{i + {1}}} }}N_{{{\text{i}} + {1},p - {1}}} {(}u{)}} \hfill \\ {{\text{defined}}\frac{{0}}{{0}}{ = 0}} \hfill \\ \end{array} } \right.$$

(2)

{N_i,p(u)} and {N_j,q(u)} are the nonrational B-spline basis functions defined on U and V, respectively. The knot vectors of U and V are presented as:

$${\varvec{U}} = \left\{ {\underbrace {0, \ldots ,0,}_{p + 1}u_{p + 1} , \ldots ,u_{r - p - 1} ,\underbrace {1, \ldots ,1}_{p + 1}} \right\}\quad \left( {r = n + p + 1} \right)$$

(3)

$${\varvec{V}} = \left\{ {\underbrace {0, \ldots ,0,}_{q + 1}u_{q + 1} , \ldots ,u_{s - q - 1} ,\underbrace {1, \ldots ,1}_{q + 1}} \right\}\quad \left( {s = m + q + 1} \right)$$

(4)

Furthermore, the piecewise rational basis function of {R_i,j(u,v)}can be defined as follows:

$$R_{i,j} (u,v) = \frac{{N_{i,p} (u)N_{j,q} (v)w_{i,j} }}{{\sum\limits_{k = 0}^{n} {\sum\limits_{l = 0}^{m} {N_{k,p} (u)N_{l,q} (v)w_{k,l} } } }}\quad (0 \le u,v \le 1)$$

(5)

As a result, Eq. (1) can be rewritten as:

$${\varvec{S}}(u,v) = \sum\nolimits_{i = 0}^{n} {\sum\nolimits_{j = 0}^{m} {R_{i,j} (u,v){\varvec{P}}_{i,j} } }$$

(6)

Assuming that:

$${\varvec{S}}(u,v) = \frac{{{\varvec{w}}(u,v){\varvec{S}}(u,v)}}{{{\varvec{w}}(u,v)}} = \frac{{{\varvec{A}}(u,v)}}{{{\varvec{w}}(u,v)}}$$

(7)

The derivative of S(u,v) can be computed as follows:

$$\begin{aligned} {\varvec{S}}_{\alpha } (u,v) & = \frac{{{\varvec{A}}_{\alpha }^{{}} (u,v){\varvec{w}}(u,v) - {\varvec{A}}(u,v){\varvec{w}}_{\alpha }^{{}} (u,v)}}{{{\varvec{w}}^{2} (u,v)}} \\ & = \frac{{{\varvec{A}}_{\alpha }^{{}} (u,v){\varvec{w}}(u,v) - {\varvec{S}}(u,v){\varvec{w}}(u,v){\varvec{w}}_{\alpha }^{{}} (u,v)}}{{{\varvec{w}}^{2} (u,v)}} \\ & = \frac{{{\varvec{A}}_{\alpha }^{{}} (u,v) - {\varvec{S}}(u,v){\varvec{w}}_{\alpha }^{{}} (u,v)}}{{{\varvec{w}}(u,v)}} \\ \end{aligned}$$

(8)

here α denotes u or v.

A^(k,l) can be calculated using Eq. (9):

$$\begin{aligned} {\varvec{A}}^{(k,l)} & = [({\varvec{wS}})^{k} ]^{l} = \left( {\sum\limits_{i = 0}^{k} {{\text{C}}_{k}^{i} {\varvec{w}}^{(i,0)} {\varvec{S}}^{(k - i,0)} } } \right)^{l} \\ & = \sum\limits_{i = 0}^{k} {{\text{C}}_{k}^{i} \sum\limits_{j = 0}^{l} {{\text{C}}_{l}^{j} {\varvec{w}}^{(i,j)} {\varvec{S}}^{(k - i,l - j)} } } \\ & = {\varvec{w}}^{(0,0)} {\varvec{S}}^{(k,l)} + \sum\limits_{i = 1}^{k} {{\text{C}}_{k}^{i} {\varvec{w}}^{(i,0)} {\varvec{S}}^{(k - i,l)} } + \sum\limits_{j = 1}^{l} {{\text{C}}_{l}^{j} {\varvec{w}}^{(0,j)} {\varvec{S}}^{(k,l - j)} } \\ & \quad + \sum\limits_{i = 1}^{k} {{\text{C}}_{k}^{i} \sum\limits_{j = 1}^{l} {{\text{C}}_{l}^{j} {\varvec{w}}^{(i,j)} {\varvec{S}}^{(k - i,l - j)} } } \\ \end{aligned}$$

(9)

So, S^(k,l) can be expressed as follows:

$${\varvec{S}}^{(k,l)} = \frac{1}{{\varvec{w}}}\left( {{\varvec{A}}^{(k,l)} - \sum\limits_{i = 1}^{k} {{\text{C}}_{k}^{i} {\varvec{w}}^{(i,0)} {\varvec{S}}^{(k - i,l)} } - \sum\limits_{j = 1}^{l} {{\text{C}}_{l}^{j} {\varvec{w}}^{(0,j)} {\varvec{S}}^{(k,l - j)} } - \sum\limits_{i = 1}^{k} {{\text{C}}_{k}^{i} \sum\limits_{j = 1}^{l} {{\text{C}}_{l}^{j} {\varvec{w}}^{(i,j)} {\varvec{S}}^{(k - i,l - j)} } } } \right)$$

(10)

where

$$\frac{{\partial^{k + l} }}{{\partial^{k} u\partial^{l} v}}A(u,v) = \sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{m} {N_{i,p}^{k} N_{j,q}^{l} {\varvec{P}}_{i,j}^{w} } } \quad ({\varvec{P}}^{w} = w{\varvec{P}})$$

(11)

$$\frac{{\partial^{k + l} }}{{\partial^{k} u\partial^{l} v}}w(u,v) = \sum\limits_{i = 0}^{n} {\sum\limits_{j = 0}^{m} {N_{i,p}^{k} N_{j,q}^{l} {\varvec{w}}1_{i,j} } } \quad ({\varvec{w}}1 = {\varvec{w}})$$

(12)

3 Principle of BEM-TRC for NURBS Surfaces

3.1 The Principle of BEM-TRC

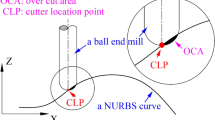
In the milling of a NURBS surface employing a BEM, the over-cut phenomenon will happen when the TRC function is not utilized during programming. The over-cut is inevitable when a CNC program controls the cutter location point (CLP) of a BEM to run along a predefined tool path. This is why the TRC function is vital in the CNC milling process. Oriented to 3-axis CNC milling machines, the TRC can be carried out by offsetting a point S on a NURBS surface one R distance (R is the radius of a BEM) along its normal vector n (as shown in Fig. 1a) under the condition that the cutter shaft can not be changed.

Fig. 1

The milling procedure and BEM-TRC of a NURBS surface, a normal vector calculation of a point on a NURBS surface, b the schematic of the milling procedure of a NURBS surface, c the milling procedure with/without BEM-TRC

The tangent vectors of τ_u and τ_v at the S point (as shown in Fig. 1a) can be calculated as follows:

$${\varvec{\tau}}_{u} = {\varvec{S}}_{u} \left( {u,v} \right)$$

(13)

$${\varvec{\tau}}_{v} = {\varvec{S}}_{v} \left( {u,v} \right)$$

(14)

here τ_u and τ_v are the tangent vectors in u and v directions, respectively. Hence, the normal vector of S point can be written as follows:

$${\varvec{n}} = {\varvec{\tau}}_{u} \times {\varvec{\tau}}_{v} = {\varvec{S}}_{u} \left( {u,v} \right) \times {\varvec{S}}_{v} \left( {u,v} \right)$$

(15)

A milling method of a NURBS surface can be performed by controlling the cutter to move in v or u direction. For example, the milling process can be carried out through controlling the cutter to cut materials along a NURBS curve (in v direction, 0 ≤ v ≤ 1) on the NURBS surface using a specific u value (as shown in Fig. 1b).

The milling of a NURBS surface can be considered as the comprehensive cutting effect of many NURBS curves on the surface. As a result, the milling of a NURBS curve is the milling basis of the corresponding NURBS surface. Figure 1c shows the schematic of the milling procedure for a NURBS curve using a BEM with and without TRC. When a BEM cuts a NURBS curve without using the TRC function, the CNC program will manipulate the CLP c of the cutter to move along the NURBS curve. For example, when a BEM cuts the cutting point (CP) a on the NURBS surface, the CNC program will manipulate the BEM-CLP to cut the CP a. This makes the CNC program to manoeuvre the cutter to locate the B position (as shown in Fig. 1c). It will lead to over-cut phenomenon inevitably due to the non-zero curvature at the CP a. Adjusting the pose of the cutter can avoid the over-cut phenomenon successfully. Unfortunately, 3-axis CNC milling machines are unable to realize the pose adjustment of the cutter. Consequently, offsetting the cutter at the CP a is the only feasible way to avoid over-cut phenomenon.

In order to perform the BEM-TRC function, the CP a should be offset one R distance to the CCP b along its normal vector n as shown in Fig. 1c. The CCP b of the cutter can be computed as follows:

$${\varvec{b}} = {\varvec{S}} + R{\varvec{n}}$$

(16)

here R is the radius of the BEM.

Then the CLP of the cutter can be calculated according to the CCP b. This makes the cutter to locate to the position A (as shown in Fig. 1c). Thus, a CNC program can be generated according to the CLP c of the cutter, which can be obtained as follows:

$${\varvec{c}} = {\varvec{b}} - R\left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]$$

(17)

This makes the hemisphere of the BEM to be tangent to the NURBS surface at the CP a. Hence, the over-cut phenomenon can be avoided accordingly.

3.2 The Interpolation and Accuracy Control for BEM-TRC

Figure 2 shows the point cloud model of a NURBS surface. Its control point (P), weight (w), knot vectors (U and V) and degree (p × q) are defined as outlined in Appendix A.

Fig. 2

The point cloud model of a NURBS surface

In order to accomplish the milling of the NURBS surface (as shown in Fig. 2) using the BEM-TRC function. The complete procedure includes three steps:

• (1) The CPs on the NURBS surface are computed using the equi-arc length interpolation (EALI) meeting the precision requirement. Based on our previous research on NURBS interpolation, the EALI can be realized by employing the fixed step plus golden section interpolation (FS + GSI) [21].

• (2) The BEM-TRC is executed at the CPs of the NURBS surface.

• (3) The BEM-CLP is computed according to the BEM-CCP.

Summarily, the flowchart of the BEM-TRC function for NURBS surfaces based on 3-axis CNC milling machines is illustrated in Fig. 3.

Fig. 3

The flowchart of the BEM-TRC function for NURBS surfaces based on 3-axis CNC milling machines (Δ is fixed step, s is assigned arc length)

Figure 4 shows the tool paths and milling effects of the NURBS surface (as shown in Fig. 2) with BEM-TRC using various (s_u0, s_v) values. As can be observed in Fig. 4, the distribution of interpolation points is even along NURBS curves when the EALI method is employed, and the interpolation precision can be controlled well. Additionally, the smaller the assigned arc length s is, the better approximation of tool paths to the contours of the NURBS surface can be obtained.

Fig. 4

The simulation results of EALI with BEM-TRC for a NURBS surface (R = 3 mm). a, c and e The tool paths with (s_u0, s_v) = (2, 5), (2, 3) and (2, 1), respectively. b, d and f The cutting effects with (s_u0, s_v) = (2, 5), (2, 3) and (2, 1), respectively

When the expected arc length s is assigned, an important problem is whether the error between the actual arc length s_i and the assigned arc length s can reach the desired accuracy. Figure 5 shows that the s_i-s curves lay inside the range of [-1 1] × 10⁻³, which meets the milling accuracy requirement.

Fig. 5

The error of s_i-s in v direction of the NURBS surface, as_v = 5, bs_v = 3

Figure 6 illustrates the paths of BEM-CLP with and without BEM-TRC. Apparently, paths without BEM-TRC don’t coincide with those of BEM-TRC. The red paths are NURBS curves on the NURBS surface corresponding to explicit u values. When the milling is performed without BEM-TRC, the BEM-CLP follows the red paths and the over-cut phenomenon happens. If the over-cut phenomenon is avoided, the BEM-CLP have to move along the green paths. Accordingly, it makes the BEM-CP to move along the red curves. Thus, the paths of the BEM-CLP (BEM-CP) deviate from (coincide with) the NURBS curves to be cut, respectively.

Fig. 6

The paths of the BEM-CLP with and without BEM-TRC (R = 3 mm), a 3D-view, b XY view

In the interpolation researches, the interpolation accuracy is a matter of great concern. When a line segment sequence approaches a NURBS curve, the chord d can denote the interpolation accuracy and be calculated as follows [22]:

$$d = \frac{{\left| {{\text{I}} \times {\varvec{C}}_{x} (u_{t} ) + {\text{J}} \times {\varvec{C}}_{y} (u_{t} ) + {\text{K}}} \right|}}{{\sqrt {{\text{I}}^{2} + {\text{J}}^{2} } }}$$

(18)

here

$$u_{t} = \left( {u_{i} + u_{i + 1} } \right)/2$$

$${\text{I}}x + {\text{J}}y + {\text{K}} = 0$$

$$I = \frac{1}{{{\varvec{C}}_{x} (u_{i + 1} ) - {\varvec{C}}_{x} (u_{i} )}}$$

$${\text{J}} = - \frac{1}{{{\varvec{C}}_{y} (u_{i + 1} ) - {\varvec{C}}_{y} (u_{i} )}}$$

$${\text{K}} = - \frac{{{\varvec{C}}_{x} (u_{i} )}}{{{\varvec{C}}_{x} (u_{i + 1} ) - {\varvec{C}}_{x} (u_{i} )}} + \frac{{{\varvec{C}}_{y} (u_{i} )}}{{{\varvec{C}}_{y} (u_{i + 1} ) - {\varvec{C}}_{y} (u_{i} )}}$$

According to Eq. (18), the chord d curves of s = 1 mm and 0.3 mm with u = 0.2, 0.5 and 0.8 are shown in Fig. 7. The smaller the arc length s (or the curvature) is, the higher the interpolation accuracy is. Additionally, the d-curve appears pluses at u =  ~ 0.25 and ~ 0.75. This results from the cusps of NURBS curves of the NURBS surface.

Fig. 7

The chord curves of various s values with u = 0.2, 0.5 and 0.8, as = 1 mm, bs = 0.3 mm

3.3 The Application of BEM-TRC

The simulation results based on Vericut software with and without BEM-TRC are shown in Fig. 8. The digital model in simulation is generated by fitting point cloud model. The maximum and average fitting error is 0.0707 mm and 0.0086 mm, respectively. The over-cut analysis error is set to be 0.071 mm. As can be observed in Fig.a and b, the milling effects without and with BEM-TRC are very good. However, there are large over-cut regions (red regions) without BEM-TRC as shown in Fig. 8a. Contrarily, when BEM-TRC is used, the over-cut phenomenon is avoided successfully as shown in Fig. 8b, and undercut regions appear. Fortunately, the undercut can be decreased using smaller radius BEMs. Table 1 outlines various model volumes with and without BEM-TRC. The volume of the digital model is 92,370.2015 mm³. The over-cut volume without BEM-TRC is − 152.3945 mm³, while the residual volume with BEM-TRC is 283.8702 mm³. Figure 8a, b and Table 1 show that BEM-TRC can avoid over-cut phenomenon.

Fig. 8

The milling simulation results based on Vericut software with s_u0 = s_v = 0.3, a, b The over-cut check results without and with BEM-TRC, respectively. (R = 3 mm, The red and blue denotes over-cut and undercut, respectively). (Color figure online)

Table 1 The comparison of volumes with and without BEM-TRC

In order to verify the algorithm of BEM-TRC of NURBS surfaces, a part corresponding to Fig. 8b is machined based on a XK715D 3-axis CNC milling machine (Manufactor: Hanchuan CNC Machine Tool Co., LTD, China) equipped with FANUC 0i-MB CNC system. Figure 9 displays the milling result of the part with BEM-TRC. Figures 8 and 9 demonstrate that the BEM-TRC algorithm proposed in this work is effective and feasible in the milling process of NURBS surfaces using BEMs for 3-axis CNC milling machines.

Fig. 9

The milling results based on a 3-axis CNC milling machine (R = 3 mm). a 3D-view. b XY view

4 Conclusion/Recommendation

Aiming at 3-axis CNC milling machines with 2D-TRC for FEMs, a new TRC named BEM-TRC is presented in this work, and the relative algorithm for BEM-TRC is given. The BEM-TRC can realize the TRC function of NURBS surfaces when BEMs are used. The execution process can be divided into two steps as follows:

• (1) Search the cutting point on the NURBS surface using equi-arc length interpolation in u or v direction.

• (2) Fulfill BEM-TRC at a cutting point (CP) through offsetting the CP to the cutter center point (CCP) of a BEM along its normal vector.

• (3) The cutter location point (CLP) of the BEM can be calculated according to the BEM-CCP.

A special toolbox based on Matlab software is obtained to execute the relative algorithm, and to generate CNC programs for FANUC CNC system. Using the toolbox, a CNC milling program of a predefined NURBS surface corresponding to BEM-RC can be obtained for a 3-axis CNC milling machine.

The simulation based on the Vericut software and experiment based on a 3-axis CNC milling machine equipped with FANUC 0i-MB confirms that the BEM-TRC of NURBS surfaces is feasible and effective. The BEM-TRC extends the 2D-TRC function of FEMs to BEMs, and makes 2D-TRC to be able to accomplish the milling of NURBS complex surfaces. The interpolation method with BEM-TRC can be applied to NURBS complex surfaces, and has broad application prospects for 3-axis CNC milling machines.

Appendix A

The parameters of P, w, U, V, p and q for the NURBS surface shown in Fig. 2 are listed as follows. P is control point, w is weight, U and V are kont vectors, and p and q is degree.

• P = {[30 0 0], [30 − 30 0] , [0 − 30 0], [− 30 − 30 0], [− 30 0 0], [− 30 30 0], [0 30 0], [30 30 0], [30 0 0]; [26 0 3], [26 − 26 3], [0 − 26 3], [− 27 − 27 1], [− 27 0 1], [− 27 27 1], [0 26 3], [26 26 3], [26 0 3]; [24 0 3], [24 − 24 3], [0 − 22 3], [− 24 − 24 3], [− 24 0 3], [− 24 24 3], [0 22 3], [24 24 3],[24 0 3];

• [21 0 4], [ 21 − 21 4], [0 − 18 4], [− 21 − 21 4], [− 21 0 4], [− 21 21 4], [0 18 4], [21 21 4], [21 0 4]; [19 0 4], ]19 − 19 4],[0 − 14 4], [− 18 − 18 4], [− 18 0 4], [− 18 18 4],[0 14 4],[19 19 4],[19 0 4]; [15 0 3.5],[15 − 15 3.5], [0 − 10 3.5], [− 15 − 15 3.5], [− 15 0 3.5], [− 15 15 3.5],[0 10 3.5],[15 15 3.5],[15 0 3.5]; [12 0 3],[12 − 12 3], [0 − 7 3], [− 12 − 12 3], [− 12 0 3], [− 12 12 3],[0 7 3],[12 12 3],[12 0 3]; [7 0 2], [7 − 7 2],[0 − 4 2], [− 9 − 9 2], [− 9 0 2], [− 9 9 2], [0 4 2], [7 7 2], [7 0 2]; [− 5 0 2], [− 5 0 2], [− 5 0 2], [− 5 0 2], [− 5 0 2], [− 5 0 2], [− 5 0 2], [− 5 0 2], [− 5 0 2]};

• w = [1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1; 1 0.707 1 0.707 1 0.707 1 0.707 1];

• U = [0 0 0 1/4 1/4 1/2 1/2 3/4 3/4 1 1 1];

• V = [0 0 0 1/4 1/4 1/2 1/2 3/4 3/4 1 1 1];

• p = 2;

• q = 2.