Atmospheric Wind Estimation Using Adaptive Block James–Stein Technique for Higher Range Coverage in MST Radar

Abstract

Measuring atmospheric winds over longer ranges using VHF-MST radar is extremely useful for studying stratosphere-troposphere exchange. The present study uses an adaptive block technique (ABlockJS), a mixed model of a parametric technique, and a few non-parametric techniques to address this aspect. The signal estimates are substantiated with five moments and six quality-related parameters while deriving three wind components along with horizontal wind speed and direction. The parametric part of the technique improves the signal, while the non-parametric part lowers noise variance. This technique is established using NARL MST Radar experimental data. The computed wind components derived from this technique are verified with the independent wind components acquired from the concurrent GPS radiosonde in-situ observations. It is observed that this analytical technique can deliver wind components more precisely and consistently, covering longer ranges of 25.20 km. It enhances the benchmark range coverage of 21.45 km attained using Fourier-based estimators on the MST dataset. The complete procedure is developed in C# from scratch without using any standard routine from available packages, thus, it fits acquisition-time application needs fine. It benefits various atmospheric research which demands higher range coverage using VHF radar.

Introduction

Atmospheric radars in the VHF band, around 50 MHz, can deliver three-dimensional Wind (Zonal Component, Meridional Component, and Vertical Component). Substantial fluctuations in the refractive index of the troposphere water vapour and temperature mainly cause MST radar return signals. Additionally, turbulence around mesospheric ranges, electron density patterns, and fluctuations in temperature in the lower stratospheric regions can all affect the return signals. All these factors contribute to the radar signals and are expected to provide useful radar returns covering the complete troposphere and lower stratosphere up to 30 km (Hocking, 1985). Typically, the FFT-based retrieval techniques provide Wind up to a maximum altitude of 21.45 km. While using the MST radar, the signal strength is generally poor, between 10 and 14 km (Ravindrababu et al., 2014). Earlier authors employed approaches on a former MST radar setup (Rao et al., 1995). In general, the FFT-based procedures have been applied and utilized preferably since the inception of this radar data. The radar now incorporates several recent architectural changes (Rao et al., 2020) and is equipped with digital receivers, allowing continuous data acquisition across beams, making data segmentation feasible. Thus, older references (techniques) for analyzing MST radar signals do not fit because new signal and noise characteristics have evolved with the changes, imposing several difficulties in implementing earlier analytics on the new dataset.

Parametric, non-parametric, semiparametric, sub-space, and mixture model-based techniques can all be selectively utilized to derive the power spectrum for MST signal. Compared to the parametric approach, the non-parametric approach is considered safer. Even in the event of insufficient data, the parametric models yield spectral estimates that are both high-performing and high-quality. However, if the noise spectrum alters, it could provide inaccurate estimations and affect the precision of the measurement. To prevent inconsistencies that could occur from using only parametric models, this study currently uses a combination model comprising both a parametric method and a few non-parametric methods.

The use of thresholding empirical wavelet coefficients makes wavelet approaches flexible. As a similar method, a procedure can retain or discard wavelet coefficients group by group by using block thresholding. Compared to conventional Wavelet techniques, which threshold the empirical coefficients term by term depending on their magnitudes, it increases estimation precision (Antonaidis & Fan, 2001). The Block method is a powerful technique that effectively balances variance and bias by utilizing the underlying information present in the neighbouring wavelet coefficients. The overlapping block thresholding estimators were developed earlier (Cai & Silverman, 2001) and used for density estimation (Chicken & Cai, 2005). When the block size is around logn, an estimator can adapt both locally and globally. In this study, we investigated Stein’s Unbiased Risk Estimate (SURE) in wavelet regression, specifically about fixed block size thresholding term-by-term with L = 1 (Donoho & Johnstone, 1995) and L = logn (Chicken, 2005). The performance of any block thresholding estimator is tunable by selecting an appropriate threshold level and block size. The local block thresholding approach uses a specified block size with a specific threshold value and applies a unique thresholding rule across all resolution levels. The orthogonal discrete wavelet transformation (DWT) resolves the non-parametric regression problem into a problem of estimating the wavelet coefficients. A few attempts (Babu & Sreenivasulu, 2019; Thatiparthi et al., 2009) towards introducing new techniques to this MST radar dataset with wavelets remained as case studies.

Whenever any FFT-based technique is used to derive Wind, the results can typically be derived only up to 21.45 km. The radar needs additional transmitting power and more processing Gain to achieve a better range. As the transmitting power of the radar is a design time problem, it is not easy to enhance higher power for transmitters, which demands physical modification of the radar. In this article, we explored the possibilities of enhanced processing gain by developing a derived dataset that uses the existing radar base dataset to attain higher range coverage without enhancing the transmit-power gain for the first time. We have strictly maintained the time uniformity between the base and the derived dataset for an eligible performance comparison. Earlier, we authors have attempted (Padhy et al., 2023, 2024) using Bayesian mixed models for post-processing, which requires greater computing power with model assumptions. The de-trending eliminates DC in raw data (Franke et al., 1988). This article delivers a non-Bayesian technique for the real-time usage needs, which is free from model assumption and initializations.

Out of several advanced techniques developed and tested recently, we present four additional techniques besides the FFT-based and ABlockJS in this article. It formulates the mentioned technique and demonstrates it from simulation to performance evaluation, with five moments and six quality parameters. It improves signal strength while reducing noise to a great extent. The technique covered are ABlockJS (T_ABlockJS), Burg (T_BRG), Pseudo-Spectrum (T_PSS), Yule-Walker (T_YWR), Multitaper (T_MTP), and FFT (T_FFT). The higher range coverage attained using this technique provides ample opportunity to investigate several atmospheric phenomena. The set of All Techniques represents ([T_ABlockJS, T_BRG, T_PSS, T_MTP, T_YWR and T_FFT]), and the Other Techniques represents ([T_BRG, T_PSS, T_MTP, T_YWR and T_FFT]). The set of All Beams represents ([East, West, Zenith, North, and South]), and the set of Other Beams represents ([West, Zenith, North, and South]) in the following sections. Appendix contains the Annexure simulation, and technique figures along with the abbreviations used in this manuscript.

Materials and Methods

Availability of Code and Data

The data and code can be downloaded anonymously from the public repository at https://www.narl.gov.in/datacenter/ABlockJS, hosted by NARL Datacenter. This includes colour figures, extra figures, and data in netCDF (.nc) format. The code is accessible in the public repository: https://github.com/manasnarl/BlockJSMST. The code is developed in C# from scratch, and it does not use any standard package like Matlab or Python to attain the highest liberty over processing. Thus, it does not depend on any standard available routines, whose internals are unknown, that vary with time through versions, affecting stored analytical results. Moreover, when written from scratch, the code gives parallel execution benefits amongst available cores in the computer, making the code fit to run in the runtime during data acquisition, thus significantly benefiting data processing.

Methodology

The following section describes six such strategies and elaborates on how to estimate the Normal mean using the ABlockJS (${T}_{ABlockJS}$). The supplementary Sect. S1.1 describes the same using Other Techniques, such as Burg (${T}_{BRG}$), Pseudo-Spectrum (${T}_{PSs}$), Yule-Walker (${T}_{YWR}$), Multitaper (${T}_{MTP}$), and FFT (${T}_{FFT}$). The supplementary Sect. S1.2 describes estimating five Moments and six Quality-based parameters. The supplementary Sect. S1.3 elaborates on the derivation of Wind.

The data-driven adaptive BlockJS technique (Cai, 2002, Cai & Zhou, 2009) has significant advantages over traditional wavelet thresholding-based estimators that employ fixed block sizes. It is a wavelet regression procedure that empirically varies the thresholding level and the block size at every resolution level while minimizing SURE. This technique uses L = logn, based on the generalization by Chicken and Cai for adaptiveness.

The ${T}_{BRG}$, fits an autoregressive (AR) model to the input data. It minimizes both the forward and backward least squares prediction errors and constrains the AR parameters satisfying Levinson-Durbin recursion (Kay, 1988). For short data records, it produces a stable model with high resolution. However, in this method, the Peak locations depend highly on the initial phase information. Burg experiences spectra line-splitting for the sinusoids under noise with increasing order, whereas the spectral width increases with less order, though Doppler is not directly affected.

The ${T}_{PSS}$, evaluates the pseudo-spectrum by using a correlation matrix for a signal, which follows Schmidt’s Eigen-space analysis method (Marple et al., 1989). This technique analyses Eigen-space on the signal correlation matrix to assess its frequency content. This algorithm can be more beneficial for signals formed as a sum of sinusoids while contaminated with some white Gaussian noise as an additive.

The ${T}_{YWR}$ employs autocorrelation to reduce the least squares forward prediction error (Hayes, 2009). It produces a suitable model, like ${T}_{BRG}$ but can’t perform better for shorter data records. The Yule-walker technique has the potential to distort frequency estimates for sinusoids buried in noise. The autocorrelation matrix is always certain to be positive-definite; hence, this technique is non-singular by property due to the bias in estimate. However, this estimate bias has no effect on the accuracy with which Wind is estimated.

The ${T}_{MTP}$, averages modified periodograms obtained using tapers (family of mutually orthogonal windows). It reduces the periodogram variability and produces a consistent power spectral density estimate (PSD) (Thomson, 1982). It makes use of the complete signal in each modified periodogram. The orthogonality of the sinusoidal tapers is uncorrelated in modified periodograms. It uses a series eigenvalue to calculate a weighted average of periodograms. It does not, however, consider the frequency concentration of sinusoidal sequences or their interaction with random processes. The multitaper method has been explored in the earlier configuration of the MST radar dataset (Anandan et al., 2004). The ${T}_{FFT}$, derives power spectrum using fast Fourier transform (FFT) following the traditional spectral estimation technique (Rao et al., 1995). This article establishes ${T}_{ABlockJS}$ as the best technique among the discussed techniques that can obtain moments and winds from relatively higher altitudes with better analytical quality.

The Estimation of a Normal Mean Using ${{\varvec{T}}}_{{\varvec{A}}{\varvec{B}}{\varvec{l}}{\varvec{o}}{\varvec{c}}{\varvec{k}}{\varvec{J}}{\varvec{S}}}$:

Consider a non-parametric regression model

$${y}_{i} = f({ t}_{i})+\sigma { z}_{i},i =\text{ 1,2},...,n,$$

(E.1)

where ${t}_{i}= i/n,$, σ is the noise level,${ z}_{i}$, represents a Normal independent variable.

This Adaptive Block Estimator estimates an unknown regression function $f\left(\cdot \right)$ on sample $\left\{{y}_{i}\right\}.$ Let the observed data be x_i such that

$${x}_{i}={\theta }_{i} +{z}_{i},\text{ where}{z}_{i}\stackrel{i.i.d.}{\Rightarrow }N\left(\text{0,1}\right), i=\text{1,2},\dots ,d.$$

(E.2)

The current problem estimates mean vector $\theta =\left({\theta }_{1},..,{\theta }_{d}\right)$ at single resolution level while estimating the mean of a Normal Bivariate variable $x = ({x}_{1},..,{x}_{d})$ where the average mean squared error is shown in

$$R\left(\widehat{\theta ,} \theta \right)= {d}^{-1}\sum_{i=1}^{d}E{\left({\widehat{\theta }}_{i}-{\theta }_{i}\right)}^{2}.$$

(E.3)

A Normal mean problem occupies a central position in statistical estimation theory.

The ${T}_{ABlockJS}$ estimates the mean θ using a block-wise James–Stein (BlockJS) estimator having block size $L$ and threshold level $\lambda$, which is chosen empirically while minimizing SURE. It thresholds the observations in groups and makes concurrent decisions on all of the means present within a single block. Let $L \ge 1$ represent viable length for each block, and

$$m = d/L$$

(E.4)

Represent the number of blocks be an integer. Fix both the block size and threshold level (L and λ) and start to divide the observations $({x}_{1},..,{x}_{d})$, which are segregated to blocks with size = L. Let, ${\underline{x}}_{b}=({x}_{\left(b-1\right)L+1,\dots ,}{x}_{bl})$, represent observations found in the bth block, which is similar with

$${\underline{\theta }}_{b}=({\theta }_{\left(b-1\right)L+1,\dots ,}{\theta }_{bl})$$

(E.5)

where ${\underline{\theta }}_{b}$ representing coefficients for the bth block and the block energy ${\underline{z}}_{b}$ found in bth block,

$${\underline{z}}_{b}=\left({z}_{\left(b-1\right)L+1,\dots ,}{z}_{bl}\right).$$

(E.6)

Let ${S}_{b}^{2}={{||\underline{x}}_{b}||}_{2}^{2} ,$ for $b=\text{1,2},\dots .m.$ The block-wise James–Stein estimator is represented as.

$$\underline{{\hat{\theta }}}_{b} \left( {\lambda ,L} \right) = \left( {1 - \lambda /S_{b}^{2} } \right) + \underline {x}_{b} \;{\text{for}}\;b = 1,2 \ldots \ldots ,m,$$

(E.7)

where λ ≥ 0 represents the threshold level. The resulting estimator is tuned optimally for (L, λ), i.e., block size and threshold level. The optimality is achieved empirically by minimizing SURE. If we write, ${\underline{\widehat{\theta }}}_{b}\left(\lambda ,L\right)={\underline{x}}_{b}+ g({\underline{x}}_{b}),$ $where g\left({\underline{x}}_{b}\right)=\left(1-\lambda /{S}_{b}^{2}\right)+{\underline{x}}_{b}, {\prime}g{\prime}$ is a function that ranges from ℝ^L–ℝ^L. Stein has demonstrated that, when ${\prime}g{\prime}$ is weakly differentiable, and so as ${\underline{x}}_{b}$, weakly differentiable. The total unbiased risk is estimated to be.

${{E}_{\theta }||\widehat{\theta }\left(\lambda ,L\right)- \theta ||}_{2 }^{2}={E}_{\theta }\text{SURE}\left({\underline{x}}_{b},\uplambda ,\text{L}\right) ,$ where$\text{SURE}(x,\lambda ,L)=\sum_{b=1}^{m}\text{SURE}\left({\underline{x}}_{b},\uplambda ,\text{ L}\right)$.

If ${T}_{d}={d}^{-1}\sum ({x}_{i}^{2}-1), {\gamma }_{d}= {d}^{-0.5}{\text{log}}_{2}^{1.5} d and {\uplambda }^{F}=2L \text{log}d.$ Let, $\left({\uplambda }^{*},{\text{L}}^{*}\right)$, represent the SURE minimizers reducing search range

$$\left({\lambda }^{*},{L}^{*}\right)=\genfrac{}{}{0pt}{}{\mathit{arg}\mathit{min}}{\mathit{max}\{L-\text{2,0}\}\le \lambda \le {\lambda }^{F} ,1\le L\le {d}^{0.5}}\mathit{ }SURE\left(x,\lambda ,L\right).$$

Now, the ABlockJS Estimator is

$$\underline{{\hat{\theta }}}_{b}^{*} = \underline{{\hat{\theta }}}_{b} \left( {{\uplambda }^{*} ,{\text{L}}^{*} } \right)\;{\text{if}}\;T_{d} > \gamma_{d} .$$

The degenerate BlockJS estimator initialized with block size L = 1 is

$$\widehat{ \theta }_{i}^{*} = \left( {1 - 2{\text{log}}d/x_{i}^{2} } \right) + x_{i} \;{\text{if}}\;T_{d} \le \gamma_{d} .$$

To apply wavelet regression to the data represented by the model $\left(E.1\right)$, the data is first transformed to the wavelet domain using DWT: $\widetilde{Y }= W.{\text{n}}^{-0.5}\text{Y}$. Considering the resolution level at $j$ for the regression function$f$, let $\widetilde{\underline{Y}}$ and${\underline{\theta }}_{j}$, denote the Empirical and the True wavelet coefficients, which are represented by ${\widetilde{\underline{Y}}}_{j}=\{ {\widetilde{y }}_{j,k}:k=1,\dots \dots {2}^{j} \}$ and ${\underline{\theta }}_{j}=\left\{ {\theta }_{j,k}:k=1,\dots \dots {2}^{j} \right\},$ respectively. At each resolution$, j$, estimate the wavelet coefficients using the estimator ${\widehat{\theta }}^{*}$ as ${\underline{\widehat{\theta }}}_{j}= {\sigma }_{n} .{\widehat{\theta }}^{*}$(${\sigma }_{n}^{-1}{ \widetilde{\underline{Y}}}_{j}$), where ${\sigma }_{n}= {\text{n}}^{-0.5}\sigma ,$ and the estimate of the whole function $f$ is given by,

$${\widehat{f}}^{*}\left(t\right)= {\sum }_{k=1}^{{2}^{j0}}{\widetilde{\upxi }}_{jo,k}{\Phi }_{jo,k}\left(t\right) + {\sum }_{j=j0}^{J-1}{\sum }_{k=1}^{{2}^{j}}{\widehat{\theta }}_{j,k}{\uppsi }_{j,k}\left(t\right)$$

(E.8)

The function at the sample points $\underline{f}=\left\{ f\left(i/n\right):i=1,\dots .,n\right\}$ is estimated finally by the inverse wavelet transform on the de-noised wavelet coefficients: $\underline{\widehat{f}}= {W}^{-1}$. ${\text{N}}^{-0.5} \widehat{\Theta }$

Estimation of a Normal Mean Using Other Techniques, Moments, Quality, and Wind

The PSD estimation methods using Other Techniques (${T}_{BRG},{T}_{PSS}, {T}_{YWR}$, ${T}_{MTP},$ $and {T}_{FFT}$) are elaborated in the supplementary Sect. S1.1a:1e. Moments and Quality estimation procedures (${{M}_{DPR},{M}_{ODW}, M}_{FSN}{,Q}_{BAP},{Q}_{NPO},{Q}_{SNDR},{Q}_{NDP},{Q}_{SFDR}, and {Q}_{SPP}$) is elaborated in the supplementary Sect. S1.2a:2e. The supplementary Sect. S1.3 elaborate on the Wind computation formula. S1.4 explains the complete ABlockJS algorithm to derive Wind from the Raw data.

The Model parameter(s)

The Blockjs model is configured with sym8 at level5 wavelet coefficients with level-independent noise.

estimation using the JameStein thresholding rule, which provides enhanced adaptivity and delivers reasonable performance. The ${T}_{BRG}$ and ${T}_{YWR}$, models are configured with an order of 64. The ${T}_{PSS}$ model is constructed with 64 order with a non-overlapping window with a length set for 128. Finally, the ${T}_{MTP}$ model is constituted with a two-taper sinusoid.

The Model and Segment Dataset

These models above take the segment dataset as input and produce the segmented output. For reducing variance by a factor of $1/k$, $k$ segments are averaged, each with a modified-nFFT length of 512 samples rather than the FFT length of 256 sample points. Non-overlapped segments usually guarantee maximum data independence. The bias decreases as segment length increases (L ≤ modified-nFFT of 512), and the noise variance decreases as the number of segments formed during estimation increases; however, the bias is not solely dependent on segment length; it also depends on the All Techniques $({T}_{ABlockJS}{,T}_{BRG},{T}_{PSS}, {T}_{YWR}$, ${T}_{MTP},$ $and {T}_{FFT}$).

Algorithm

Brief Algorithm Title: ABlockJS on Single Segment

• Input: Segment data ${S}_{sig}$, wavelet parameters (${nlvl}_{5}$,sym8, James–Stein Threshold rule, and Linear Independent) for ABlockJS using Eq. (1)

• Step1. Decompose ${S}_{sig}$, using Multi Signal Wavelet Decomposition using Eq. (2).

• Step2. Calculate Adaptive Block James–Stein ABlockJS ${Y}_{Sig}$.

• 2.1. Calculate normalization Factor normf using Eq. (3)

• 2.2. Repeat 2.2.1–2.2.4 to calculate ABlockJS threshold for at all nlvl levels.

• 2.2.1. Estimate each block viable length to be used for the ABlockJS using Eq. (4)

• 2.2.2. Estimate the coefficients using Eq. (5) for each block found using Eq. (4)

• 2.2.3. Estimate the block energy of b using Eq. (6)

• 2.2.4. Estimate block-wise James–Stein coefficients at threshold level using Eq. (7).

Calculate ${Y}_{sig}$ by Using Multi-Signal Wavelet Reconstruction at ${nlvl}_{5},$ Using Eq. (8).

Output: Finally, store ${Y}_{Sig}$ for current ${S}_{sig}$

Detailed Algorithm Title: ABlockJS Technique

Algorithm Estimating Wind (using ${T}_{ABlockJS}$ on Raw IQ dataset), is elaborated in detail in the supplementary Sect. S1.4. It uses these highlighted eight equations. The software follows this detailed algorithm step by step, which is commented precisely as per the algorithm steps, for easy understanding.

Experiment Information and Data Availability

A clear air day was purposefully chosen for experimentation to establish the ABlockJS technique using NARL MST radar to ascertain limited wind variation, circumventing the turbulence effect that could rise during non-clear air conditions. It lets wind components be derived using MST for a better comparison with the GPS radiosonde that provides wind components.

Date of experiment: 29 APR 2022 (Two hours and 30 min).

Data is available on demand from the NARL data centre. The netcdf (.nc) file is available online, as mentioned earlier. The base dataset and the derived dataset information are provided below.

Dataset Information (Base Data)

Pulse width (PWD)	16 µs
Baud length (Baud)	1 µs
Inter-pulse period (IPP)	320 µs
Duty	5.12%
Number of Fourier points nFFT	256
Number of coherent integrations NCI	256
Doppler frequency	− 6.10 Hz: + 6.10 Hz
Doppler velocity	− 17.27 m/s: + 17.27 m/s
The number of range-bins	180
Range resolution	150 m
Beam tilt angle	10°
Frequency resolution	0.047 Hz
Velocity resolution	0.135 m/s
Cycles	17
Expected measurement accuracy	± 2 frequency samples in 256 nFFT
Measurement error expected	± 0.27 m/s
No. of frames	425
No. of beams	5 East, West, Zenith, North, South
Number of incoherent integrations	5

Segmented Dataset Information (Derived Data)

Segments	12
Derived nFFT	512
Window	Kaiser
Kaiser kβ	5.85
Improved velocity resolution	0.067 m/s
Improved frequency resolution	0.0235 Hz
Expected measurement accuracy	± 2 frequency samples in 512 nFFT
Improved measurement error expected	− ± 0.135 m/s

Timing Uniformity in Beams and Cycles

Timing uniformity is ensured for the analysis of the approaches presented in this manuscript while performing segmentation. The segments are formed across incoherent integrations to improve processing, a newly introduced concept to improve SNR and reduce noise optimally, explained in the next section.

No. of Cycles in base and derived dataset = 17.

The cycle duration of timing details in both datasets = 00 h:08 m:45 s.

In both datasets, each cycle contains = 5 (i.e., All Beams).

where, Each beam comprises 5 incoherent integration.

The segmentation was carried out across these five incoherent integrations.

Each Beam Duration is calculated to be 00 h:01 m:45 s.

Similarly, the Moment parameters duration corresponds to one beam 00 h:01 m:45 s;

and the duration of the Quality parameters corresponds to one beam 00 h:01 m:45 s.

Results

This manuscript establishes the ABlockJS technique for estimating Atmospheric Wind. The technique results are evaluated based on the performance in the following two steps.

Step 1: Study the stepwise signal enhancement using Simulation (ABlockJS vs. FFT).

ABlockJS with single-segment simulation (Sect. “ABlockJS with Single-Segment Simulation”).

ABlockJS with segmentation simulation (Sect. “ABlockJS with Segmentation Simulation”).

ABlockJS Gain using segmentation simulated from − 35to − 15 dB (Sect. “ABlockJS Gain using segmentation simulated from -35dB to -15dB”).

Step 2: Signal enhancement results using experimental MST dataset (Sect. “Signal enhancement results using experimental MST Dataset”).

ABlockJS with Single-Segment Simulation

Consider normalized Raw IQ signals that constitute a complex signal with 512 sample points termed nFFT, with injected Doppler at 2 Hz, added with white Gaussian noise with -16.5 dB. This 512-sample dataset is termed as Segment Dataset. Single Segment Simulation and the analysis are detailed in Fig. 9, which demonstrates (a) the Simulation of Raw IQ Data with one Segment and 512 nFFT, (b) the noisy IQ signal contaminated with added white Gaussian noise at − 16.5 dB and injected doppler at 2 Hz, (c) the obtained normalized segment spectrum.

The ABlockJS uses a Multi-signal 1-D wavelet Decomposition to find the coefficients as depicted in step 1 of the algorithm in Sect. “Algorithm”. The Jame-Stein threshold rule using BlockJS prior and likelihood results are described in Fig. 10 by following step 2 of the same algorithm in Sect. “Algorithm”. This figure demonstrates the use of (a) multi-signal 1-D wavelet decomposition to find coefficients for the ABlockJS procedure, (b) results after applying the Jame-Stein threshold rule using BlockJS prior and the likelihood to modify the coefficients.

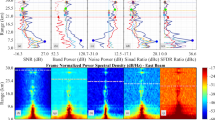
The measured SNR and the Noise power is elaborated in Fig. 1. The results of simulation after performing multi-signal wavelet reconstruction of ABlockJS are shown in Fig. 1, which demonstrates (a) the comparison of range normalized ABlockJS spectrum exhibiting less noise when compared with FFT spectrum, (b) the comparison of power spectrum exhibiting better relative gain in SNR and Noise Power while using ABlockJS than FFT while both detected doppler frequency range [− 6.10–6.10 Hz].

Fig. 1

a The comparison of range normalized ABlockJS spectrum exhibiting less noise when compared with FFT spectrum, b The comparison of power spectrum exhibiting better relative gain in SNR and Noise Power while using ABlockJS than FFT while both detected doppler frequency range [− 6.1–6.1 Hz]

The supplementary Fig. S1.5 and S1.6 demonstrate how the common raw data forms an input to the ABlockJS and FFT segment process, respectively, which is range normalized¹, how the output spectrum range normalized², power plot with harmonic³, its Noise spectrum NPxx⁴, its Noise Level L⁵, the Half band power and the 3 dB band width⁶, SINAD ratio and the distortion power⁷ and finally the SFDR and the spurious power⁸ derivation, pictorially. The picture demonstrates nine parameters such as Doppler (DPLR), Observed Doppler Width (ODW), the ratio of the fundamental signal and noise (FSN), band power averaged (BPA), Noise power (NPO), Sinad ratio (SNDR), Sinad distortion power (NDP), and Spurious Power (SPP). The Gain in [FSN, BPA, NPO, SNDR, NDP, SFDR, SPP], is calculated to be [1.34 dB, 3.16 dB, − 1.87 dB, 2.34 dBc, − 1.88 dB, 0.64 dBc, − 0.18 dB].

ABlockJS with Segmentation Simulation

Typically, the common mode dataset from the MST radar is experimented with 256 nFFT points using five incoherent integrations. Creating a collated dataset from the actual MST dataset comprising 256 nFFT points is covered widely in the supplementary segmentation simulation Sect. S2. The collated data sequence is formed from 256 nFFT samples covered vide 5 Incoherent Integration in the dataset forming 1280 nFFT sample points.

The detection hits and misses are progressively covered for the following categories: moderate, slightly above moderate, and slightly below moderate cases in Sect. S2 comprising figures S2.1:S2.12 illustrates the following four scenarios progressively.

FFT’’ case:256 sample IQ points, with 5 segments.

FFT’ case:512 sample IQ points with 5 segments.

FFT case:512 sample IQ points with 12 segments.

ABlockJS case:512 sample IQ points with 12 segments.

The consolidated results from these cases are tabulated in Table 1 and pictorially exhibited in Fig. 2, demonstrating progressive improvement from the FFT’’ case to the ABlockJS case.

Table 1 Summary of simulation results

Fig. 2

Comparison of Detectability amongst techniques with injected aWGN power with Moderate, above moderate, and below moderate threshold values for the 5 Techniques (FFT, ABlockJS) analyzed with 12 segments and 512 nFFT points. The Techniques FFT’ and FFT’’ use 5 Segments each but with 512 and 256 nFFT points, respectively

ABlockJS Gain Using Segmentation Simulated from − 35 to − 15 dB

Figure. 11 demonstrates the detectability details from 128 simulations for the input Doppler range of [− 35 to − 15 dB] analyzed using 4 Techniques (FFT’’, FFT’, FFT, ABlockJS).

Figure 3, highlighting the mean detection levels where the doppler detection is Hit ~ 90% and ~ 60% respectively in the corresponding doppler frequency range for 256 samples in FFT’’ [1.98 Hz: 2.08 Hz] and for 512 samples in FFT’, FFT, ABlockJS with doppler frequency range [1.99 Hz: 2.04 Hz].

Fig. 3

The detectability details from 128 simulations for the input Doppler range of [− 35 dB: − 15 dB] were analyzed using 4 Techniques (FFT’’, FFT’, FFT, ABlockJS), highlighting the mean detection levels where the Doppler detection is Hit ~ 90% and ~ 60% respectively in the corresponding frequency range for 256 samples in FFT’’ [1.98 Hz: 2.08 Hz] and for 512 samples in FFT’, FFT, ABlockJS [1.99 Hz: 2.04 Hz]

Signal Enhancement Results Using Experimental MST Dataset

A typical PSD (5th cycle of 17 cycles) is analyzed using ${T}_{ABlockJS}$ (Fig. 4). The frame-normalized-PSD displays signal at a relatively higher range. It shows the signal strength that varies with respect to range and doppler-frequency. The range-normalized-PSD, which allows the peak of each range that varies with range and doppler-frequency are demarcated in blue, more clearly illustrates the highest range covered. A red-dotted line in the same picture indicates the maximum range achieved of up to 25.20 km, represented by all sub-figures. Correlations later determined this limit.

Fig. 4

(E1, W1, Z1, N1, S1) represents the frame normalized PSD, whereas (E2, W2, Z2, N2, S2) represent the PSD which is normalized for range. They are obtained using the ABlockJS technique for All Beams of the fifth cycle on 29 Apr 2022 from 21 h:59 m:35 s IST to 22 h:07 m:58 s IST. Red dotted lines show the maximum range coverage of 25.20 km

The supplementary PSD Sect. S.3 comprising Figs. S3.1:S3.5 represent the similar results when examined using Burg (${T}_{BRG}$), Pseudospectrum (${T}_{PSS}$), Yule Walker (${T}_{YWR}$), Multi taper (${T}_{MTP}$), and FFT (${T}_{FFT}$) respectively. The techniques set [${T}_{BRG},{T}_{PSS}, {T}_{YWR },{T}_{MTP},and {T}_{FFT}$] represents Other Techniques, which depicts the maximum range coverage extending up to (24.00 km, 23.55 km, 21.75 km, 22.95 km, and 21.45 km), after which the trace smears up to 29.55 km significantly. The signal is quite strong in the lower altitude range, relatively less in the middle altitude range, but relatively weak in the higher altitude range. In Sect. S.3 vide fig.S3.6 elaborates on the PSD profile covering an altitude range from 2.69 to 29.55 km (East beam of All Techniques) and highlights the maximum detectable altitude by dashed lines. Section S3 comprising Figs. S3.7:S3.10 elaborates like fig.S3.6 but for Other Beams.

The range bin at 6.00 km, 13.50 km, and 24.30 km represents lower, middle, and higher altitude regions, respectively. Figure 5 exhibits these three typical range bins for the fifth cycle (All Techniques and All Beams). The lower and the middle range-bin could exhibit the fundamental peak in all the cases. However, ${T}_{ABlockJS}$ could detect peak at higher range bin though appears noisy due to not removing the noise power, whereas the denoising techniques ${T}_{BRG},{T}_{PSS},{T}_{MTP}, {T}_{YWR , }and {T}_{FFT }$ have eliminated weak signal as if they are noise. The Other Techniques and All Beams could not detect the fundamental signal properly in the higher range bin.

Fig. 5

(E1:E6), (W1:W6), (Z1:Z6), (N1:N6), and (S1:S6) represent the PSD normalized for range (${T}_{ABlockJS}{,T}_{BRG},{T}_{PSS},{T}_{MTP ,}{T}_{YWR},and {T}_{FFT}$), respectively, for All Beams of the fifth cycle on 29 Apr 2022 from 21 h:59 m:35 s IST to 22 h:07 m:58 s IST exhibiting sample range-bin at 6.00 km, 13.50 km, and 24.30 km, respectively, representing strong, moderate and weak echo regions. The detection of fundamental peaks in the higher height region that was found to be incorrect is marked in a red dot. The correct Doppler detected by the ABlockJS is demarcated with a blue dot for the higher height representative range bin at 24.30 km

The mean Gain in Quality with standard deviation is depicted in Fig. 6 (East Beams) using All Techniques. The Table 2 elaborates on the overall mean Gain in Quality using ${T}_{ABlockJS}$. The supplementary 2D Moments and Quality Sect. S4 comprising Figs. S4.1:S4.4 represent the mean Gain in Quality for the Other Beams. The Moment and Quality analysis, along with Gain, quantifies ${T}_{ABlockJS}$, as a relatively better technique than Other Techniques, with more ${M}_{FSN}$, higher ${Q}_{BPA}$, lesser ${Q}_{NPO}$, more ${Q}_{SNDR}$, better ${Q}_{SFDR}$, low ${Q}_{NDP}$, and shallow Spurious Power ${Q}_{SPP}$.

Fig. 6

a1:a9 represents the mean variation in all 17 cycles for nine selected parameters (${M}_{DPR}{{, M}_{ODW}{, M}_{FSN,} Q}_{BPA}{,Q}_{NPO},{Q}_{SNDR},{Q}_{SFDR},{Q}_{NDP}, and {Q}_{SPP}$) for All Techniques and East Beam, on 29 Apr 2022 from 21 h:24 m:37 s IST to 23 h:45 m:50 s IST

Table 2 Beam-wise quality—gain using ${T}_{ABlockJS}$ when compared To ${T}_{BRG},{T}_{PSS}$ ${T}_{MTP}, {T}_{YWR}$ and ${T}_{FFT}$

The supplementary RTI Moments Sect. S5 vide Fig. S5.1 shows the Moments RTI for ${M}_{DPR}$, ${M}_{ODW}$,${M}_{FSN}$ ${M}_{PWR, }$ and ${M}_{NLV}$ (All Techniques, and East Beam). Fig.S5.b1 illustrates that the ${M}_{ODW}$ is superior when utilizing ${T}_{ABlockJS}$, as opposed to Other Techniques, as illustrated in figs-S5.b2: S5.b6. When utilizing ${T}_{ABlockJS}$, as illustrated in fig.S5.c1, ${M}_{FSN}$ is found to be relatively higher than when utilizing Other Techniques, as illustrated in figs-S5.c2: S5.c6. The ${M}_{PWR}$ is consistent across All Techniques as exhibited in figs-S5.d1: S5.d6, however ${T}_{FFT}$, appears to lead with better signal power in fig.S5.d6, but reveals a poor noise scenario as shown in fig.S5.e6. The ${M}_{NLV}$ using ${T}_{ABlockJS}$, appears pretty clean in fig.S5.e1. The figs-S5.2:S5.5 elaborates in detail on Moments RTI to establish analytical consistency for the Other Beams derived using All Techniques.

The supplementary RTI Quality Sect. S6 vide Fig. S6.1 shows the Quality comprising (${Q}_{BPA}$, ${Q}_{NPO}$,${Q}_{SNDR}$ ${Q}_{SFDR, } {Q}_{NDP, }$ and ${Q}_{SPP}$), for the East-Beams, analyzed using All Techniques. Though ${Q}_{BPA}$ is observed to be highest while using ${T}_{FFT}$, in all these beams, it suffers more towards ${Q}_{NPO,}{Q}_{SNDR,}$ ${Q}_{SFDR}$,${Q}_{NDP}$ ${Q}_{SPP}$. The figs-S6.2:S6.5 elaborate on Quality RTI to establish consistency in analysis (Other Beams, All Techniques).

Figure 7 compares the 17-cycle mean for Wind parameters (${Wind}_{HWS}$, ${{U}_{Z},V}_{M}$) (All Techniques) with the same parameters obtained for the GPS radiosonde (${Wind}_{HWSGPS},{U}_{ZGPS},{V}_{MGPS}$). The marginal root mean square difference (RMSD) variation between the MST and GPS winds, shown in red, is attributable to wind variance throughout two and half hours of observation.

Fig. 7

a1:a6 represents ${Wind}_{HWS}$, b1:b6 represents${U}_{z}$, and c1:c6 represents ${V}_{M}$ obtained using${T}_{ABlockJS}{,T}_{BRG},{T}_{PSS}, {T}_{YWR}$, ${T}_{MTP},$ and${T}_{FFT}$, respectively, for all 17 cycles on 29 Apr 2022 from 21 h:24 m:37 s IST to 23 h:52 m:49 s IST

The supplementary RTI Wind Sect. S7 vide Fig. S7 shows the RTI parameters such as ${{U}_{Z}, V}_{M}{, W}_{V}, {Wind}_{HWS}$ and ${Wind}_{WD}$, for all 17 cycles derived using All Techniques. The Wind,${ Wind}_{HWS}$, ${Wind}_{WD}$, has reliable variation below the maximum detected altitude (horizontal dotted lines), above which the estimation is unreliable.

Figure 8a1:8a3 demonstrates the mean correlation for parameters such as ${Wind}_{HWS, }{{U}_{Z},V}_{M}$, derived using ${T}_{ABlockJS}$, to ${Wind}_{HWSGPS},{U}_{ZGPS},{V}_{MGPS},$ from 2.69 to 25.20 km with r = 0.95, 0.96, and 0.87, shows decent accuracy in measurement, while the Wind is derived using ${T}_{ABlockJS}.$ Fig. 8b1:8b3, displays the cumulative correlation of ${Wind}_{HWS}$, ${{U}_{Z},V}_{M}$([2.69–17.55 km]:[2.69–29.55 km]) derived using ${T}_{ABlockJS}$, to ${Wind}_{HWSGPS},{U}_{ZGPS},{V}_{MGPS}$. Assuming the cutoff is set for the wind parameters as ${Wind}_{HWS}=0.9, {{U}_{Z}=0.9,V}_{M} =0.85$ (demarcated red vertical dashed lines), the maximum altitude decorrelates after (25.20 km, 24.00 km, 23.55 km, 21.75 km, 22.95 km, 21.45 km) for the Wind (All Techniques). The blue dot in Fig. 8b1:b3 represents ${T}_{ABlockJS}$, confirming its better performance over Other Techniques.

Fig. 8

Subfigure, a1:a3 represents MST Wind (${Wind}_{HWS}$, ${{U}_{Z},V}_{M}$) correlation against GPS Wind (${Wind}_{HWSGPS}$ ${{U}_{ZGPS},V}_{MlGPS}$), using the ${T}_{ABlockJS}$ from 2.69 km to 25.20 km. Subfigure b1:b3 represent the cumulative correlation (([2.69 km to 17.55 km]:[2.69 km to 29.55 km]) computed between MST Wind and GPS Wind using ${T}_{ABlockJS}{,T}_{BRG},{T}_{PSS}, {T}_{YWR}$, ${T}_{MTP},$ $and {T}_{FFT}$

Similarly, the supplementary Correlation section of All Techniques S8 vide Fig. S8 depicts Wind correlation. The supplementary higher altitude profiles in Sect. S9 and S10 shows ${T}_{ABlockJS}$, compared to Other Techniques for All Beams. It elaborates on the analytical performance of ${T}_{ABlockJS}$, in the weak return range context stated in the introduction (i.e., 10.05–15.00 km) and the higher altitude weak return range (i.e., 19.95–25.50 km), is elaborated in supplementary Fig. S9 and S10, respectively, revealing improved trace detectability. The typical 2D PSD of the sample fifth cycle, highlighting the altitudes exclusively from 15.00 to 25.35 km, is shown in supplementary Fig. S11. The variation of Wind parameters at higher altitudes > 15.00 km, along with correlation mean variation in the ratio of fundamental signal and noise, is covered in supplementary Fig. S12, which proves the efficacy of the proposed technique ABlockJS, which has performed superior to the contemporary Other Techniques.

Discussion

The ABlockJS technique represents a significant advancement in the estimation of high-resolution wind components from the MST dataset. Employing a hybrid model, this method stands out for its innovative approach to data analysis. The technique’s superiority over five other methods is thoroughly discussed, highlighting its unique features and benefits. Notably, the ABlockJS technique enhances signal detection and estimation, offering a robust solution for analyzing radar signals and improving the accuracy of wind estimation at higher ranges. The study’s conclusions emphasize the effectiveness of ABlockJS in providing detailed atmospheric dynamics insights, which are crucial for advancing meteorological research and applications.

The BlockJS data-driven adaptive estimating technique significantly advances the MST Radar signal data analysis. Employing a continuous observation mode overcomes previous limitations, allowing for a novel approach to data collation that spans incoherent integration. This method enhances the signal strength for the MST radar dataset, which is particularly beneficial for capturing signals from the higher ranges where they are typically weaker.

The introduction of various moment and quality-related parameters, such as the ratio of the fundamental signal and noise (FSN), band power averaged (BPA), Noise power (NPO), Sinad ratio (SNDR), Sinad distortion power (NDP), and Spurious Power (SPP), marks a first for the NARL MST Radar, providing a comprehensive framework for evaluating both quality of signal and noise covering various techniques in the current context.

Notably, the technique achieves a 5–10 dB increase in average data-processing Gain, significantly enhancing the signal strength, the crucial factor for high-altitude data analysis.

Cross-validation with radiosonde wind measurements ensures the reliability of the data obtained through the ABlockJS technique.

Moreover, the ABlockJS technique proves especially valuable for detecting signals in weaker regions, ranging from 19.95 to 25.20 km, demonstrating its potential for enhancing the detection capabilities of MST Radar technology.

Conclusions

The advancement in MST radar technology through the ABlockJS analytical approach marks a significant milestone in atmospheric science. By extending the reference range to 25.20 from 21.45 km, researchers can obtain more precise 3D-wind measurements at higher altitudes. This enhancement improves the accuracy of meteorological observations and broadens the scope of various scientific studies, enabling a deeper understanding of atmospheric dynamics and improving several atmospheric studies.

Appendix

See Figs.

Fig. 9

Single Segment Simulation and Analysis: a The Simulation of Raw IQ Data with one Segment and 512 nFFT Sample Points b The noisy IQ signal was contaminated with added white Gaussian noise at − 16.5 dB and injected Doppler at 2 Hz. c The normalized segment spectrum

9,

Fig. 10

${T}_{ABlockJS}$ Simulation: a Use Multi-signal 1-D wavelet Decomposition and find coefficients for the ABlockJS procedure, b Apply the Jame-Stein threshold rule using BlockJS prior and likelihood to modify the coefficients. The coefficient of value range and the coefficient number are plotted on the Y and X-Axis, respectively

10 and

Fig. 11

The detectability (i.e., hit or miss) details from 128 simulations for the input Doppler range of [− 35 dB: − 15 dB] were analyzed using 4 Techniques (FFT’’, FFT’, FFT, ABlockJS), highlighting the mean detection levels where the Doppler detection is Hit ~ 90% and ~ 60% respectively in the corresponding frequency range for 256 samples in FFT’’ [1.98 Hz: 2.08 Hz] and for 512 samples in FFT’, FFT, ABlockJS [1.99 Hz: 2.04 Hz]

11.

See Tables 1 and 2.