Introduction

Surface reconstruction based on point cloud data is of significance in many fields including reverse engineering (Zhao et al. 2013), recording of culture heritage (Yastikli 2007), deformation monitoring (Guo et al. 2010; Xuan et al. 2016) and Building Information Model (BIM) (Anil et al. 2013). Recently, due to the great advance of modern 3D measurement technologies, a very dense point cloud can be produced rapidly by scanning the surface of a physical object. Key issues are how to deal with such large-scale point cloud datasets and memory-saving. Hence, it is point cloud simplification that needs to be performed to prune redundant points and retain the main geometric features of the object surface, any subsequent surface reconstruction would become significantly faster and easily carried out.

In recent decades, many scholars have contributed themselves to the study on point cloud simplification and have made great success. According to the principle of reduction, the existing point cloud simplification methods can be divided into two categories: mesh-based simplification and point-based simplification (Han et al. 2015). Mesh-based methods implement the point cloud simplification by constructing polygonal meshes (triangular meshes or quadrilateral meshes) and then removing the vertexes of redundant meshes according to some rules (Hur et al. 2002; Luebke 2001). The disadvantage of such methods is that the mesh generation is complex and time-consuming. Compared to those algorithms, point-based methods operate the simplification directly on the data points without any meshes to be generated. Zheng (2006) proposed a uniform simplification algorithm. The method could simplify point cloud with a high speed and a simple procedure, but it would miss the consideration of the geometry features. Then some non-uniform simplification methods with geometric guarantees were presented. Moenning and Dodgson (2003) devised coarse-to-fine feature-sensitive simplification algorithms for uniform and non-uniform distributed point cloud with density guarantee. Pauly et al. (2002) generalized and compared some popular methods in mesh simplification to the point cloud case: clustering methods, iterative simplification and particle simulation. Shi et al. (2011) presented an adaptive simplification method using k-means clustering, and the proposed method could generate uniformly distributed sparse sampling points in the flat areas and necessary higher density in the high curvature regions. Benhabiles et al. (2013) proposed a fast algorithm to simplify point cloud based on the combination of both clustering and coarse-to-fine approaches. This method could simplify point cloud with high density of points in sharp regions and low density in flat regions as well. Song and Feng (2009) and Han et al. (2015) both put forward an iterative method with preserved edge data. After edge points were identified, the least important data point among the non-edge points would be deleted from the point cloud.

A common core among these non-uniform simplification methods is to evaluate the importance of each point in point cloud. The simplification can be easily achieved by removing the less important points (Linsen 2001; Kalaiah and Varshney 2003). As is well known, normal vector is basic information of point cloud, and can be obtained expediently. Moreover, the angles between the normal vectors of its neighboring points could describe the local geometric characteristic. Hence, this paper proposed a new simplification method based on the normal angles in point cloud. The local entropy of normal angle would be calculated in order to quantify the importance of each point. Because of the advantage of the accurate control of reduction ratio, the proposed method would accomplish the simplification in a progressive way.

The Proposed Simplification Method

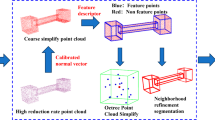
In this section, the proposed simplification method will be introduced elaborately. Figure 1 shows the general flowchart of the proposed method. For each point, we first estimate the normal vector based on the nearest neighboring points, then measure the importance and remove the least important point gradually using local entropy of normal vector angle, finally, the ultimate decimated point cloud can be generated according to the user-designed simplification ratio. To measure quantitatively the accuracy of the simplification method, an indicator is proposed by calculating the mean entropy of the simplified point cloud.

Fig. 1
figure 1

General flowchart of the proposed simplification algorithm

Full size image

Normal Vector Estimation

Normal vectors play an important role in representing surface of objects, and they are often employed as the necessary input information when processing point cloud data.

The classic and simple PCA (Principal Components Analysis) method for estimating normal vector was presented by Hoppe et al. (1992) in order to reconstruct a surface better by fitting a local plane. For a point p and its k-neighboring points, the fitted local plane P is computed by Eq. (1).

$$ P\left( {n_{p} ,d} \right) = \mathop {\arg \hbox{min} }\limits_{{\left( {n,d} \right)}} \sum\limits_{i = 1}^{k} {\left( {n_{p} \cdot p_{i} - d} \right)^{2} } $$
(1)

where \( n_{p} \) is the normal vector of the plane P, d is the distance from P to the origin of coordinate, \( p_{i} \) is the ith point of the k-neighboring points of point p.

Plane P contains point p and the centroid of its k-neighboring points, and normal vector n meets the constraint \( \left\| n \right\|^{2} = 1 \), so the fitting problem could be simplified to eigenvalue decomposition of the positive semi-definite covariance matrix M in Eq. (2).

$$ M = \frac{1}{k}\sum\limits_{i = 1}^{k} {\left( {p_{i} - \bar{p}} \right) \cdot \left( {p_{i} - \bar{p}} \right)^{T} } $$
(2)

where \( \bar{p} \) is the centroid of the k-neighboring points of point p. The eigenvector of the smallest eigenvalue is the value of normal vector of point p.

Progressive Point Cloud Simplification

Progressive point cloud simplification would be implemented on the basis of evaluating the importance of points in point cloud. Then point cloud could be simplified by removing the least important point and updating normal vectors and importance values, progressively.

Evaluating the Importance of a Point

In this section, the importance of a point in point cloud would be assessed by calculating local entropy of normal angle.

To express normal angle more conveniently, the included angle between the normal vector and a reference plane would be adopted instead of those between adjacent normal vectors. Suppose that the input point cloud is \( X = \left[ {\begin{array}{*{20}c} {x_{i} } & {y_{i} } & {z_{i} } \\ \end{array} } \right]^{T} ,\quad i =\, 1,2, \ldots ,n. \), the reference plane could be obtained with the method of the orthogonal total least squares, which can be formulated by Eq. (3).

$$ a_{r} \left( {x - \bar{x}} \right) + b_{r} \left( {y - \bar{y}} \right) + c_{r} \left( {z - \bar{z}} \right) + d_{r} = 0 $$
(3)

where \( \bar{x} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {x_{i} } \), \( \bar{y} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {y_{i} } \), \( \bar{z} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {z_{i} } \); \( a_{r} \), \( b_{r} \), \( c_{r} \) and \( d_{r} \) are the parameters of the reference plane.

The normal angle \( \theta \) of point p in point cloud could be calculated by Eq. (4)

$$ \theta = \frac{\pi }{2} - \arccos \left( {\frac{{n_{p} \cdot n_{r} }}{{\left| {n_{p} } \right| \cdot \left| {n_{r} } \right|}}} \right) $$
(4)

where \( n_{p} \) is the normal vector of point p, and \( n_{r} = \left( {\begin{array}{*{20}c} {a_{r} } & {b_{r} } & {c_{r} } \\ \end{array} } \right) \) is the normal vector of the reference plane.

Then the normal angles of the k-neighboring points of point p can be computed in this way, which are indicated as \( \theta_{1} ,\theta_{2} , \ldots ,\theta_{k} \). For the point p, the information entropy of the normal angle can be defined by its k-neighboring points, as shown by Eq. (5).

$$ I\left( p \right) = H\left( \theta \right) = - P_{\theta } \log P_{\theta } - \sum\limits_{i = 1}^{k} {P_{{\theta_{i} }} \log P_{{\theta_{i} }} } $$
(5)

where

$$ P_{\theta } = \frac{\theta }{{\theta + \sum\nolimits_{i = 1}^{k} {\theta_{i} } }},\quad P_{{\theta_{i} }} = \frac{{\theta_{i} }}{{\theta + \sum\nolimits_{i = 1}^{k} {\theta_{i} } }}, $$

\( P_{\theta } \) is the probability of the normal vector of point p, and \( P_{{\theta_{i} }} \) is the probability of the normal vector of the ith neighboring point.

The local entropy of normal angle indicates how important the point is in representing the local geometric feature. A large value means that the point locates in a region where the concave, and convex change obviously and the local geometry would change if this point is removed. Therefore, the point plays an important role in describing the local geometric feature and must be retained. A small value, on the contrary, suggests that the point locates in a flat region, so the point can be represented by its neighbors and could be removed.

Removing the Least Important Point Progressively

The simplification of point cloud be achieved by progressively removing the least important point according to the value calculated by Eq. (5). After removing a point from point cloud, the adjacent configurations of the removed point would change, so the updating process of the normal vectors and importance values of the affected neighboring points should be executed. With the updates of the affected normal vectors and importance values, the simplification algorithm would continue to remove the next least important point. The simplification would be terminated with the specified number of points reached.

Updating Normal Vectors and Importance Values

As briefly stated previously, the removal of a point from the point cloud would lead to the change of its neighborhood configurations, so the normal vectors of these neighboring points should be re-estimated. In addition, the importance evaluation of a point is based on its neighborhood and normal vectors, so the importance values should be updated.

According to Song and Feng (2009) and Han et al. (2015), the impact of removing a point can be limited to a small group of points in the neighborhood of the point. After the removal of a point, the points whose normal vectors need to be updated form the first ring of the removed point. The impact on importance values of removing a point may go even further. The points whose importance values need to be re-estimated would not only the points on the first ring but also those on the second ring of the removed point.

An Indicator for Evaluating the Accuracy of Simplification

To evaluate the results of point cloud simplification, three indicators including algorithm efficiency, simplification rate and accuracy should be analyzed comprehensively.

Generally, evaluating the accuracy of simplification is accomplished by comparing the scatter figures of point clouds between the original data and the simplified one, which would lead to a subjective and unstable conclusion. An excellent simplification method may focus on retaining more features with a smaller number of points, so how to evaluate the accuracy of simplification could be converted to measuring the information quantity of point cloud (Yang et al. 2015). The local entropy of normal angle of a point in point cloud calculated can be used to analyze how important the point is to describe the local surface shape. Also, it can be used to measure the information quantity of the simplified point cloud. For any point in the simplified point cloud, the information entropy of normal angle could be calculated by

$$ H_{i} = - P_{i} log_{2} P_{i} - \sum\limits_{j = 1}^{k} {P_{j} log_{2} P_{j} } $$
(6)

where

$$ P_{i} = \theta_{i} /\left( {\theta_{i} + \sum\limits_{j = 1}^{k} {\theta_{j} } } \right),\quad P_{j} = \theta_{j} /\left( {\theta_{i} + \sum\limits_{j = 1}^{k} {\theta_{j} } } \right), $$

In the equation, \( \theta_{i} \) is the normal angle of point i in the simplified point cloud, \( \theta_{j} \) is the normal angle of the jth neighboring point of the point i, \( P_{i} \) and \( P_{j} \) are the probability distribution of the normal angle of the point i and j, respectively.

Therefore, a mean entropy of the simplified point cloud could be obtained by averaging the total information entropy of normal angle,

$$ \bar{H} = \sum\limits_{i = 1}^{n} {{{H_{i} } \mathord{\left/ {\vphantom {{H_{i} } n}} \right. \kern-0pt} n}} $$
(7)

where n is the number of the points in the simplified point cloud. A higher value would indicate that the simplified point cloud data includes more important points, and the simplification method completes the data reduction with a higher accuracy.

Experiments and Results

To assess the effectiveness and performance of the proposed approach, two validation experiments were carried out. The first experiment was implemented to inspect the performance of the proposed method preserving curved surface data during simplification. In the second experiments, another real case was employed to validate the effectiveness of the presented method. All the input point clouds used in the experiments were acquired by the RIEGEL-VZ400. The accuracy of the vertical angle, horizontal angle, and range is 0.002°, 0.008°, and 2 mm, respectively. For each validation experiment, the simplification results by the proposed method would be compared with those results by three classical methods: equidistant method, bounding-sphere method and curvature-based method. With a same simplification ratio set, the comparisons would be conducted in two aspects: algorithm efficiency and accuracy. The data processing platform is Windows 7 on laptop PC 1.8 GHz processor and 4 GB memory.

Experiment I and Results

In the first experiment, a basketball and a plane board were scanned to represent the features of curved surface (sphere) and flat plane, respectively, as shown in Fig. 2a.

Fig. 2
figure 2

The input point cloud data: a the scanned basketball and plane board; b the original point cloud of the basketball and plane board

Full size image

By editing the raw data of the scanned scene, the input point cloud data just containing the curved surface and flat plane was prepared, as shown in Fig. 2b. The total number of the input point cloud is 182,191 where the flat plane is 147,876 and the curved surface is 34,315, respectively. The simplification ratio was firstly set to 10%. After simplified with the four mentioned methods, the results are depicted in Fig. 3. The simplification times are shown in Table 1.

Fig. 3
figure 3

The simplification results with the four methods: a the proposed method; b the equidistant method; c the bounding sphere method; d the curvature-based method

Full size image
Table 1 Simplification times of different methods for ball and plane data
Full size table

In Table 1, we can see that the equidistant method takes the least time, the second is the proposed method, which is very close to the equidistant method, and the curvature-based method does the worst performance in time-consuming.

The number of the points belonging to the flat plane and the curved surface are counted and shown in Table 2. As shown in Fig. 3 and Table 2, more points at the region of curved surface has been preserved with the proposed approach and the curvature-based method, while the method of equidistant and bounding-sphere removed these points from the curved surface region, even holes appear on the surface, as described in Fig. 3b.

Table 2 Simplification results of different methods for ball and plane data
Full size table

To assess the simplification accuracy of the four methods, the fitting could be operated for the plane and curved surface. Table 3 shows the results of the fitting operations.

Table 3 Fitting results of different methods for ball and plane data
Full size table

As we can see in Table 3, in the point clouds simplified with the proposed and curvature-based approach, more sphere points have been retained, so the precisions of the fitted sphere radius are higher. And the precisions of the fitted plane seems to be almost equal in all the four cases. In order to evaluate the accuracy more applicative to other cases, the mean entropy of the simplified point clouds could be obtained according to Eqs. (6) and (7). For the purpose of feasibility validation, the information quantity of point cloud obtained by Yang’s approach (Yang et al. 2015) would be adopted for comparison. Figure 6 shows the results of information quantity of the four simplified point clouds calculated with two methods.

As shown in Fig. 4, it verifies the feasibility of the proposed mean-entropy method that the results of the information quantity calculated with two different methods reveal a similar trend. Moreover, each set of results shown in Fig. 4 suggest that the proposed method keep the most information during the simplification process, and the curvature-based method comes in the next. The equidistant and bounding sphere method do the worst. The results of the fitting operations agree with those calculations, where the effectiveness of the indicator to evaluate the accuracy of simplification could be proved again. So, the simplification accuracy of the proposed method are the highest among the employed four methods.

Fig. 4
figure 4

Results of information quantity of the four simplified point clouds calculated with two different methods: a the proposed mean-entropy method; b Yang’s method

Full size image

According the results of the four methods in aspects of simplification time and accuracy, we can draw some preliminary conclusions that: for a point cloud containing regular features, the simplification accuracy of the proposed method and the curvature-based method are higher than the other two methods. And the speed of the proposed method is almost close to that of the equidistant method which is the fastest. Hence, the proposed method do better performance in simplification time and accuracy. For the point cloud containing more complex features of irregular patterns, further validation of the effectiveness and performance of the proposed approach would be performed in the next experiment.

Experiment II and Results

In the second experiment, a lion sculpture, as shown in Fig. 5a, was scanned to acquire the point cloud representing complex features of irregular patterns.

Fig. 5
figure 5

The scanned lion sculpture (a) and the original point cloud data (b)

Full size image

The total number of the points in the lion data is 457,124, as shown in Fig. 5b. The detailed features locating at the region of the face and feet are very complicated that would make big trouble to the simplification method. Different simplification ratios for the lion data were set from 20 to 80% with an interval of 20%. After simplified with the four mentioned methods, the results of simplification ratio 20%, are depicted in Fig. 6. The simplification times are shown in Table 4.

Fig. 6
figure 6

Simplification results with the four methods, the reduction ratio was set at 20%: a the proposed method; b the equidistant method; c the bounding sphere method; d the curvature-based method

Full size image
Table 4 Simplification times of different methods for lion data
Full size table

In Table 4, we can see that the four methods do the similar performance with that in experiment I in time-consuming. The proposed method is a little lower efficient than the equidistant method which is still the fastest. As depicted in Fig. 6, the results of the simplification ratio 20% demonstrate that the proposed method shows the better performance in preserving more feature points at the region of face and feet than other methods. To measure the accuracy of the simplification results at different ratios obviously, information quantity of the simplified point clouds would also be calculated with two different method, as show in Fig. 7.

Fig. 7
figure 7

Results of information quantity of different simplified point clouds calculated with two different methods: a the proposed mean-entropy method; b Yang’s method

Full size image

Figure 7a shows the results of the information quantity of the point clouds computed by the proposed mean entropy method. The point clouds were simplified with the four method at different reduction ratios from 20 to 80%. As shown in the figure, it can be concluded that: (1) the value of information quantity decreases with the reduction of the number of the points in point cloud; (2) for an identical object and a same reduction ratio, the proposed simplification method could preserve more information quantity than other three methods, in other words, the simplification accuracy of the proposed method would be the highest among the four methods. Figure 7b depicts those results of the information quantity of the point clouds computed by the Yang’s method, where the validity of the above analysis could be proved.

Discussion and Conclusion

In this paper, a new progressive simplification method for point cloud has been proposed based on the theory of information entropy and normal angle. The core of the method is evaluating the importance of points using the information entropy of the normal angle. The normal angle is obtained by estimating the normal vectors on the basis of the classical PCA algorithm. The simplification is completed by progressive removal of the least important points and updates of the importance values. To assess the accuracy of the simplification method, an indicator for quantitatively measuring information quantity of point cloud has been determined by calculating the mean entropy of the simplified points. According to the results of the experiments where two style of point cloud data were employed, the feasibility and performance of the proposed method has been analyzed and proved. The experimental results also show that the proposed approach has three main advantages: First, the reduction ratio is easy to be reached by the progressive way. Second, the accuracy of ours is higher than curvature-based method, equidistant method and bounding sphere method. Third, the average of the importance values of the points in the simplified point cloud could be used to measure the accuracy of simplification process. Despite that, the proposed method still needs to be validated in more cases to test its applicability.