Introduction

Extreme events are phenomena whose occurrence was not expected by humans, and man-made structures are incapable of handling them and so are often vulnerable because the ecosystems and physical structures of human societies are regulated by normal climatic conditions. Therefore, it can be concluded that climate change events are one of the most serious challenges across the world today (CCSP 2008). Heavy rains (floods), abrupt temperature changes (drought), and unexpected seasons are examples of these events (Meehl et al. 2000). These events can occur at different time and location scales and may include one or more climatic variables such as temperature, rainfall, flow, and water level, which indicates their complexity.

Based on the special report of the intergovernmental panel on climate change (IPCC) on the management of the dangers of extreme events and natural hazards (Field et al. 2012), global warming can have severe effects on climatic extremes such as changes in their frequency, intensity, and spatial pattern. Also, several studies have been investigated the extreme temperature in Iran that they show increasing trend of temperature significantly (Zamani and Berndtsson 2018; Babaeian et al. 2019; Moghaddasi et al. 2022). The past few decades have witnessed a substantial increase in climatic extremes, including heavy precipitation events and extreme hot days (Alexander et al. 2006; Vose et al. 2005). Several studies have focused on cases of climate extremes like heavy rainfall and severely hot days in different temporal and spatial scales (Jakob 2013; AghaKouchak et al. 2013; Diffenbaugh and Giorgi 2012; Kharin et al. 2007; Easterling et al. 2000). Records show concordance of various extremes such as hot-dry and hot-humid conditions in the last decades of the second millennium. For example, the global mean surface temperature is predicted to increase by about 3 °C in the next century (Ejder et al. 2016). There is an even larger increase in the probability of extreme temperature events (Mearns et al. 1984; Katz and Brown 1992; Perkins et al. 2012) and the frequency and intensity of hydro-climatological extreme events (Mirza 2003; Linnenluecke et al. 2011; Young 2013; Tian et al. 2016). It is expected that the frequency, duration, and intensity of extreme heat events will increase in a future warmer climate (IPCC 2012).

Applying concepts such as return period and return level, under the assumption of a stationary climate, would yield valuable knowledge for planning, decision-making, and estimation of the impacts of unusual weather and climatic events (Rosbjerg and Madsen 1998). But, due to the change in the frequency of extreme values, there is a need for approaches and concepts that are applicable in the non-stationary analysis of climate and hydrological extreme values (Parey et al. 2010; Cooley 2013; Salas and Obeysekera 2013). Frequency analysis is used to investigate the probability of the occurrence of extreme events in a given return period (Gilroy and McCuen 2012). The regional frequency analysis of extreme values is usually determined by two approaches: annual maximum series (AMS), also called block maxima (BM), and peak-over threshold (POT). The generalized extreme value (GEV) and generalized Pareto distribution (GPD) are used as probability distributions for values selected with AMS and POT methods, respectively (Katz et al. 2002; Hawkes et al. 2008; AghaKouchak and Nasrollahi 2010; Li et al. 2015).

There are two approach for estimating of distribution parameters including Bayesian and classical. The choice between a Bayesian and classical approach is then often motivated by the problem at hand. The Bayesian approach allows for a more convenient way of dealing with parameter uncertainty when using estimation results for decision making, for example, in forecasting exercises. In a classical framework (such as MLE method), one often has to rely on bootstrapping techniques. Another advantage of the Bayesian approach arises if the model to be analyzed contains unobserved or latent variables such as, for example, unobserved states describing the stage of the business cycle, missing variables, or the unobserved volatility in a stochastic volatility model. The Bayesian analysis allows for a natural way to conduct inference on the unobserved variables, where again parameter uncertainty is taken into account. The MCMC and DE-MC methods are based on Bayesian approach (Paap 2002).

A great deal of research has been done on extreme temperatures, and some of which are mentioned in the following. Gao and Zheng (2018) utilized quantile regressions to illustrate the annual temperature extremes and to correlate them with two other weather models of the western Pacific subtropical high (WPSH) and the Arctic Oscillation (AO) in 357 metrological stations in China. In this study, all statistical data such as WPSH (or AO) and prominent positive graphs between warm (or cold) temperature extremes have been analyzed in most of the metrological stations. Finally, the optimal model with the minimum Bayesian information criterion (BIC) was chosen from among 16 nominated constructed GEV distribution models. The periods 1961–1980 and 1991–2010 were computed and estimated based on the 20-year return levels of annual warm (or cold) extremes. The outcomes confirmed the deterministic effect of the trend and distribution changes on the 20-year return levels of variations in annual warm and cold extremes.

Raggad (2018) worked on two numerical studies using the maximum temperature information collected from 15 Saudi Arabian meteorological stations during 1985–2014. The amalgamation of those two approaches resulted in a model by Raggad, which ascertains the effects of diachronic changes on the evaluation of return level and justifies the utilization of the non-stationary generalized extreme value distribution method to modify most of the findings.

Gabda et al. (2018) presented a theory to deduce the distribution of the investigated temperature extremes and their subsequent changes over time by using the findings of climatological data. This research employed the annual maximum perceived temperatures from all 439 sites on a 25-km spatial network in the UK in the 1960–2009 period. It confirmed that using observed information would significantly reduce uncertainty in evaluating historical and future changes in extreme temperature. Aziz et al. (2020) investigated the temporal variability in yearly and seasonal extreme temperatures across Turkey using stationary and non-stationary frequency analysis. The analyses were conducted using generalized extreme value (GEV) and normal and Gumbel distributions for minimum and maximum temperatures during historical (1971–2016) and projection (2051–2100) periods. Magnitudes of non-stationary impacts (30-year return level) show strong spatial and seasonal variability. Notably, higher magnitudes are observed for minimum temperature (up to + 10 °C) than maximum temperature (up to + 4 °C). Such positive impacts are more significant particularly in eastern Turkey for yearly and seasonal scales. This effect shows greater regional variability in the historical period but, with increased temperature projection, it is more homogenous and larger in the future period for each region.

The main goal of the present study is to compare extreme value theory (EVT) approaches for frequency analysis of temperature in Arak plain, central Iran, as the case study. For this aim, the monthly maximum temperature was first collected from the CRU. In this regard, two commonly used approaches were used including block maxima (BM) or the annual maximum series (AMS) approach and the peaks-over-threshold (POT) approach to extract time series of maximum temperature. Moreover, some nonparametric trend and stationarity tests were employed for the 1901–2016 period. By fitting the GEV model, the distribution parameters were estimated using the DE-MC method. It is worth noting that the most common estimation methods utilized in previous studies on extreme values were based on either the method of moments or the maximum likelihood. Therefore, the novelty of this research includes (1) temperature frequency analysis based on differential evolution Markov chain (DE-MC) approach and (2) application of two methods to derive time series of extreme maximum temperature. In addition, previous studies have not investigated the non-stationary behavior of extreme temperatures in the central Iranian plateau.

Methodology

Case study and dataset

Markazi province, located in the central part of Iran, is known as the industrial capital of this country. Its climate is warm and dry, with average annual rainfall and temperature of 261 mm and 14.6 °C, respectively. In this province, the most important and the largest plain is the Arak plain, known as the Meyghan desert, wherein enormous industrial and agricultural activities are based. The extent of this basin is 5460 km2, and 3100 km2 of which is flat and the rest is mountain-outs. Meyghan wetland is one of the 10 major wetlands in Iran, which is located in the middle of this area (Fig. 1).The research temperature data were collected from the nearby synoptic stations, including Arak, Gavar, Sarugh, Ashtian, and Shanagh. The research datasets included Climate Research Unit (CRU) and station-based observations. The CRU gridded dataset produces time series of monthly climate variables from 1901 to 2016 with a 0.5-degree spatial resolution (New et al. 1999; Mitchell and Jones 2005). These datasets are generated from monthly ground-based climate variables over land and are interpolated through inverse distance weighting (IDW). This research work used the monthly maximum temperature from this dataset (https://data.ceda.ac.uk).

Fig. 1
figure 1

The case study

Full size image

Methodology

An overview of the methodology of the current research is as follows (Fig. 2):

Fig. 2
figure 2

The research flowchart

Full size image

Extraction methods of extreme series

In EVT, there are two fundamental approaches, both widely used: the block maxima (BM) or annual maximum series (AMS) (a specific case of BM for yearly blocks) method and the peaks-over-threshold (POT) method (Ferreira and Haan 2015). The BM approach consists of dividing the observation period into nonover-lapping periods of equal size and restricts attention to the maximum observation in each period Gumbel (1958). In POT approach, one selects those of the initial observations that exceed a certain high threshold. The probability distribution of those selected observations is approximately a generalized Pareto distribution (Pickands 1975).

Stationary analysis tests

Augmented Dickey-Fuller (ADF) test

The augmented Dickey-Fuller (ADF) test can assess stationary. Here, H0 hypothesizes that the time series is stationary, while H1 signifies a non-stationary time series (Banerjee et al. 1993). ADF test was applied at each station to assess stationary in time series at the 95% level of confidence using Eq. (1).

$$\Delta xn=\alpha+\beta t\;+\;\gamma xt-1+\sum\left(\delta t\Delta xt-\;\right)\;p\;j=1+et\;\left(1\right)$$
(1)

where ∆x is the differenced series at a lag of n years, α is the drift, β is the coefficient on a time trend, p is the lag order autoregressive process, γ represents the process root coefficient, δt represents the lag operator, and et is the independent identical distribution residual term with mean = 0 and variance σ2 = 0.

Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test

The null hypothesis here is the stationary of time series around mean or a linear trend, while the alternative hypothesis assumes a non-stationary time series because of the existence of a unit root (Kwiatkowski et al. 1992). Time series Y1, Y2, …, Yn can be decomposed to a deterministic trend (βt), random walk (rt), and stationary error (εt):

$${\mathrm Y}_{\mathrm t}={\mathrm r}_{\mathrm t}+{\mathrm\beta}_{\mathrm t}+{\mathrm\varepsilon}_{\mathrm t}$$
(2)
$${\mathrm r}_{\mathrm t}={\mathrm r}_{\mathrm t-1}+{\mathrm u}_{\mathrm t}$$
(3)

For time series Yt with a deterministic stationary trend, the null hypothesis is expressed as \({\sigma }_{U}^{2}=0,\) meaning that the intercept is a fixed component, against the alternative of a positive \({\sigma }_{U}^{2}\). For this case, the residual error \({e}_{t}={\epsilon }_{t}\), where \({e}_{t}={Y}_{t}-\overline{Y }\) and \({Y}_{t}={r}_{0}+{\beta }_{t}+{\varepsilon }_{t}\) (H0). The H1 specifies that \({e}_{t }={r}_{t }+{\varepsilon }_{t}\), which means the process has a unit root. The general form for the KPSS test is as follows:

$$\mathrm{KPSS}=\frac1{\mathrm T^2}{\textstyle\sum_{\mathrm t=1}^{\mathrm t}}\frac{{\mathrm s}_{\mathrm t}^2}{{\widehat\sigma}_\infty^2}$$
(4)
$${\mathrm s}_{\mathrm t}={\textstyle\sum_{\mathrm j=1}^{\mathrm t}}\;{\mathrm e}_{\mathrm j}$$
(5)
$$\widehat\sigma{}_\infty^{\;\;\;2}\;=\;\lim\nolimits_{\mathrm t\rightarrow\infty}\;\mathrm{var}\;\left({\textstyle\sum_{\mathrm t=1}^{\mathrm t}}\;{\mathrm r}_{\mathrm t}\right)$$
(6)

Pettitt’s test

The Pettitt’s test is based on the Mann–Whitney two-sample test (rank-based test) and allows the detection of a single shift at an unknown time t (Pettitt 1979). The null hypothesis is no change in the distribution of a sequence of random variables; the alternative hypothesis is that the distribution function F1(x) of the random variables from X1 to Xt is different from the distribution function F2(x) of the random variables from Xt+1 to XT. Hence:

$$D_{ij}=\mathrm{sgn}\;\left(X_i-X_j\right)=\left\{\begin{array}{c}-1\;(X_i\;-\;X_j)\;<0\\0\;(X_{i\;}-\;X_j)\;=0\\+1\;(X_i\;-\;X_j)\;>0\end{array}\right.$$
(7)

where Xi and Xj are random variables with Xi following Xj in time. The test statistic Ut,T depends on Dij as:

$${\mathrm U}_{\mathrm t},\mathrm{T}={\textstyle\sum_{\mathrm i=1}^{\mathrm t}}\;\;{\textstyle\sum_{\mathrm j=\mathrm t+1}^{\mathrm T}}\;{\mathrm D}_{\mathrm{ij}}$$
(8)

The statistic Ut,T is the same as the Mann–Whitney statistic for analyzing when the two samples X1, …, Xt and Xt+1 …, XT arise from the same population. The test statistic Ut,T is assessed for all random variables from 1 to T; then the most significant change point is selected where the value of |Ut,T| is the largest:

$${\mathrm K}_{\mathrm T}=\max\nolimits_{1\leq\;\mathrm t\;<\mathrm T}\left|{\mathrm U}_{t,\mathrm T}\right|$$
(9)

A change-point occurs at time t when the statistic KT is significantly different from zero at a given level. The approximate significant level is given by:

$$\mathrm p=2.\;\exp\;\left(\frac{-6\mathrm k_{\mathrm T}^2}{\mathrm T^2+\mathrm T^3}\right)$$
(10)

Once the p-value is less than the pre-assigned significance level α, we can reject the null hypothesis and divide the data into two sub-series (before and after the location of the change-point) with two different distribution functions.

Extrem value analysis (EVA)

A statistical distribution is fitted to a series of observations based on which the magnitude and probability of the occurrence of the variable under study are determined. It is recommended to use GEV and GPD distributions, respectively, for fitting the best function distribution on AMS and POT data.

Generalized extreme value (GEV)

The GEV distribution method can flexibly model different behaviors of extremes with three distribution parameters θ = (μ,σ,\(\varepsilon\)): (1) the location parameter (μ) shows the center of the distribution; (2) the scale parameter (σ) defines the deviation size around the location parameter; and (3) the shape parameter (ξ) oversees the tail behavior of the GEV distribution (Delgado et al. 2010). This distribution is a three-parameter model incorporating Gumbel, Fréchet, and Weibull maxima extreme value distribution (Coles et al. 2001) as in the following equation:

$${\mathrm Y}_{\mathrm t}\sim\mathrm{GEV}\left({\mathrm\mu}_{\mathrm t},{\mathrm\sigma}_{\mathrm t},{\mathrm\varepsilon}_{\mathrm t}\right)$$
(11)
$$\mathrm{GEV}\left({\mathrm\mu}_{\mathrm t},{\mathrm\sigma}_{\mathrm t},{\mathrm\varepsilon}_{\mathrm t}\right)=\left\{\begin{array}{c}\begin{array}{cc}\exp\left(\left[(1+\mathrm\xi\left(\frac{\mathrm Y-\mathrm\mu}{\mathrm\sigma}\right)\right]^\frac{-1}{\mathrm\xi}\right)&\mathrm i\mathrm f\;\mathrm\varepsilon=0\end{array}\\\begin{array}{cc}\exp\left(-\mathrm e^{-\left(\frac{\mathrm Y-\mathrm\mu}{\mathrm\sigma}\right)}\right)&\mathrm{if}\;\mathrm\varepsilon=0\end{array}\end{array}\right.$$
(12)

In non-stationary conditions, the parameters of the distribution function are time-dependent. Since modeling temporal changes in the shape parameter requires long-term observations that are often not available for practical applications, non-stationary behavior concerning the location parameter and the location and scale parameters is assumed to be a linear function of time.

$$\mathrm{GEV}\left(\mathrm\mu\left(\mathrm t\right)={\mathrm\mu}_0{+\mathrm\mu}_1\mathrm t,\mathrm\sigma,\mathrm\varepsilon\right)$$
(13)
$$\mathrm{GEV}\;\left(\mathrm\mu\left(\mathrm t\right)={\mathrm\mu}_0{+\mathrm\mu}_1\mathrm t,\;\mathrm\sigma\left(\mathrm t\right)=\exp\left({\mathrm\sigma}_0+{\mathrm\sigma}_1\mathrm t\right),\mathrm\varepsilon\right)$$
(14)

Generalized Pareto distribution (GPD)

The cumulative probability of the generalized Pareto distribution (GPD) is calculated from the following equation:

$$\mathrm{Pr}\left[\mathrm{X}<\mathrm{x}\right]\approx G(x-{u}^{^{\prime}}{\varepsilon }^{^{\prime}}\sigma )=\left\{\begin{array}{c}1-{(1-\frac{{\varvec{\upxi}}\left(x-u\right)}{\upsigma })}^{\frac{1}{{\varvec{\upxi}} }} \varepsilon \ne 0\\ 1-\mathrm{exp}\left(-\frac{x-u}{\upsigma }\right) \varepsilon =0\end{array}\right.$$
(15)

where u, \(\upxi\), and \(\upsigma\) are threshold, scale, and shape parameters, respectively.

Threshold selection

In this context, two methods are used to select the thresholds, namely MRL plot and Hill plot:

Mean residual life plot (MRL plot)

Davison and Smith (1990) introduced MRL plot to determine the threshold using the expectation of the GPD excesses:

$$\mathrm e\left(\mathrm u\right)\;=\;\mathrm E\left(\;\mathrm x-\left.\mathrm u\right|\;\mathrm x>\mathrm u\right)=\frac{\sigma_{\mathrm u}+{\mathrm\varepsilon}_{\mathrm u}}{1-\mathrm\varepsilon},\mathrm\varepsilon<1$$
(16)

where u denotes the threshold, \(\varepsilon\) denotes the shape parameter, and \({\sigma }_{u}\) denotes the scale parameter corresponding to threshold u. The condition of \(\varepsilon\) \(<\) 1 is defined to guarantee the existence of the expectation. Equation (1) shows that the expectation of excesses is linear in u with gradient \(\varepsilon\) /(1 – \(\varepsilon\)) and intercept \({\sigma }_{u}\) /(1 – \(\varepsilon\)). For a set of samples (\({X}_{1}\), \({X}_{2}\),…, \({X}_{n}\)), the empirical estimate of the mean of excesses can be obtained as follows:

$$e_n\left(\mathrm u\right)=\frac1{N_u}{\textstyle\sum_{i=1}^{N_u}}\left(X_i-u\right),X_i>\mathrm u$$
(17)

where \({N}_{u}\) denotes the number of exceedances over u. The set data of {u, \({e}_{n}\) (u)} represent the MRL plot. Generally, the value of u above which the plot is an approximately straight line can be selected as the optimal threshold.

Hill plot

Let \({X}_{(1,\mathrm{ n})}\) \(>\) \({X}_{(2,\mathrm{ n})}{>\dots >X}_{(n,\mathrm{n})}\) be associated with the descending order statistics of (\({X}_{1}\), \({X}_{2}\),…, \({X}_{n}\)), which are independent and identically distributed random variables. Assuming that the distribution of these random variables is heavy-tailed, the Hill estimator, a well-known estimator of \(\varepsilon\), is defined as:

$${\mathrm H}_{k,\;\mathrm n=}=\frac1{\mathrm k}{\textstyle\sum_{\mathrm i=1}^{\mathrm k}}\;\log\;\left(\frac{{\mathrm X}_{(\mathrm i,\mathrm n)}}{{\mathrm X}_{(\mathrm i,\mathrm n)}}\right),\mathrm k\leq\mathrm n$$
(18)

The Hill estimator is a function of these extreme random variables {\({X}_{(1,\mathrm{ n})}\),\({X}_{(2,\mathrm{ n})}\),…,\({X}_{(\mathrm{k },\mathrm{ n})}\)}, which depends on the chosen threshold. A Hill plot is constructed by the Hill estimator of a range of k values versus the k value or the threshold. The value of \({X}_{\mathrm{k},\mathrm{n}}\) above which the Hill estimator tends to be stable can be chosen as the optimal threshold (Hill 1975).

Estimating distribution parameters

In this section, the DE-MC was used to estimate the distribution parameters based on Bayesian theory. In the Bayesian method, inferences about model parameters are based on their posterior distribution, which is a combination of observed data and information from previous studies or personal experiences known as prior distribution (Renard et al. 2013; Cheng et al. 2014). Differential evolution (DE) is a simple genetic algorithm for numerical optimization in real parameter spaces. In a statistical context one would not just want the optimum but also its uncertainty. The uncertainty distribution can be obtained by a Bayesian analysis (after specifying prior and likelihood) using Markov chain Monte Carlo (MCMC) simulation. DE-MC is a population MCMC algorithm, in which multiple chains are run in parallel. DE-MC solves an important problem in MCMC, namely that of choosing an appropriate scale and orientation for the jumping distribution. In DE-MC, the jumps are simply a multiple of the differences of two random parameter vectors that are currently in the population. Simulations and examples illustrate the potential of DE-MC. In the fact, the DE-MC combines the genetic algorithm called differential evolution (DE) for global optimization over real parameter space with Markov chain Monte Carlo (MCMC) so as to generate a sample from a target distribution. In Bayesian analysis, the target distribution is typically a high dimensional posterior distribution. Both DE and MCMC are enormously popular in a variety of scientific fields for their power and general. Briefly, the advantages of DE-MC over conventional MCMC are simplicity, speed of calculation, and convergence, even for nearly collinear parameters and multimodal densities (Ter Braak 2006).

Evaluation criteria

Criteria such as the coefficient of determination (R2), root mean square error (RMSE), mean bias error (MBE), and convergence (\(\upvarepsilon )\) (Gelman and Shirley 2011) were used for data analysis and model evaluation. Their relationships are presented below:

$$\mathrm{RMSE}=\sqrt{\frac{\sum_{\mathrm{m}=1}^{\mathrm{n}}{\left({\mathrm{X}}_{\mathrm{p}}-{\mathrm{X}}_{0}\right)}^{2}}{\mathrm{n}}}$$
(19)
$${\mathrm{R}}^{2}={\left[\frac{\frac{1}{\mathrm{n}}\sum_{\mathrm{m}=1}^{\mathrm{n}}\left({\mathrm{X}}_{\mathrm{p}}-{\upmu }_{0}\right)\left({\mathrm{X}}_{\mathrm{p}}-{\upmu }_{0}\right)}{{\upsigma }_{\mathrm{Xp}}\times {\upsigma }_{\mathrm{X}0}}\right]}^{2}$$
(20)
$$\mathrm{MBE}=\frac{\sum_{\mathrm m=1}^{\mathrm n}({\mathrm X}_{\mathrm P}-{\mathrm X}_0)}{\mathrm n}$$
(21)
$${\mathrm\varepsilon}_{\mathrm i}=\frac{\left|\sum_{\mathrm i-9}^{\mathrm i-5}{\mathrm{OF}}_{\mathrm i}-\sum_{\mathrm i-4}^{\mathrm i}{\mathrm{OF}}_{\mathrm i}\right|}{\sum_{\mathrm i-4}^{\mathrm i}{\mathrm{OF}}_{\mathrm i}}$$
(22)

where Xp and Xo are the simulated and observed data, respectively, μ is the mean of the data population, σ is the standard deviation, n is the total number of data, i is the current iteration number (> 10), OFi is the objective function value in the ith iteration, and \({\varepsilon }_{i}\) is the convergence value of the objective function in the ith iteration. R2 represents the linear relationship between simulated and observed data, which is between 0 and 1. The closer to 1, R2 represents a stronger linear relationship between the simulated and observed data.

Return level and return period

The year m return level is the level where the number of expected events in an m year period is one. In the stationary state, the level of return is the same for all years, and there is a one-to-one relationship between the level of return (multiple) and the period of return (related time interval). The return level is expressed as a function of the return period T:

$$\mathrm T=\frac1{1-\mathrm p}$$
(23)

P is the occurrence probability in a defined year (assuming stationary). The return level in the stationary state is obtained as follows:

$${\mathrm q}_{\mathrm p}=\left(\left(-\frac1{\mathrm{lnp}}\right)^{\mathrm\xi}-1\right)\times\frac{\mathrm\sigma}{\mathrm\xi}+\left(\neq0\right)$$
(24)

The model parameters are used to calculate the return level in the non-stationary state as follows:

$$\widetilde{\mathrm\mu}=Q_{\mathrm K}\left({\mathrm\mu}_{\mathrm t1,}{\mathrm\mu}_{\mathrm t2},\dots,{\mathrm\mu}_{\mathrm{tn}}\right),\left(\mathrm\mu\left(\mathrm t\right)={\mathrm\mu}_{\mathrm t1}+{\mathrm\mu}_0\right)$$
(25)
$${q}_{\mathrm{p}}=\left({\left(-\frac{1}{\mathrm{lnp}}\right)}^{\upxi }-1\right)\times \frac{\upsigma }{\upxi }+ \stackrel{\sim }{\upmu } \left(\upxi \ne 0\right)$$
(26)

where k = 0.5 is the median of location parameters and \({Q}_{\mathrm{K}}\left({\upmu }_{\mathrm{t}1}, {\upmu }_{\mathrm{t}2},\dots , {\upmu }_{\mathrm{tn}}\right)\), and k = 0.95 is related to the ninth percentile of location parameters (Cheng et al. 2014). It should be noted that NEVA packages were used to perform the calculations of frequency analysis (Cheng et al. 2014).

Results

Assessment of CRU dataset

To use CRU data, their correlation with station observation-based data should be examined. To this end, the maximum monthly temperature data of the stations in the study area were extracted and compared with the observational data of the Arak synoptic station in the same period (during from 1956 to 2010). It should be noted that the nearset grid (x = 49.75, y = 34.25) to Arak synoptic station was considered for comparing purposes. The comparison results showed that these data have a high correlation (0.98) and the lowest error (1.49) with observation station-based data (Fig. 3). The data had the necessary accuracy for other stations as well.

Fig. 3
figure 3

The variation of maximum monthly temperature (observational and CRU) during 1956–2010

Full size image

Stationary analysis tests

The Mann–Kendall test was used to examine the trend of time series of extreme maximum temperature values (Mann 1945; Kendall 1975). The results showed that the τ values were from 0.25 to 0.33 indicating the independence of the temperature data from the time (Table 1). In addition, the mean son’s slope was about 0.011 that showed a significant increasing trend. Finally, as the p-value in all selected stations was less than the significance level (5%), the null hypothesis of none of the trends was rejected (Fig. 4a). As illustrated in Fig. 4, Gavar station shows an increasing trend. Then, KPSS and ADF tests were used to assess the stationarity of these time series. The results showed the time series of extreme temperature were non-stationary in all selected stations (Table 1). For instance, in Gavar station, the ADF statistic was obtained at − 2.38, i.e., lower than the critical values (0.6). The p-value was greater than the (5%) significance level, and so it is concluded that the null hypothesis of the non-stationary state should be accepted. For the KPSS test, since the p-value was 0.03 and smaller than the (5%) significance level, and the KPSS statistic was greater than the critical value (0.16), the null hypothesis was rejected (i.e., the data were stationary). Therefore, the time series data in the Gavar station was non-stationary. In the following, the homogeneity of extreme temperature was assessed using Pettit’s test over the study area. The results show that all stations were non-homogeneous, as presented in Fig. 4b for the Gavar station.

Table 1 Stationary tests for the selected stations
Full size table
Fig. 4
figure 4

The trend (a) and homogeneity (b) of extreme maximum temperature in Gavra station

Full size image

Frequency analysis of GEV distribution

In this section, Q-Q probability plot was used to fit the GEV distribution to maximum temperature (for Gavra station, Fig. 5). As illustrated in this figure, the GEV theoretical distribution is in good relation with the one obtained from the empirical distribution. This issue is also confirmed by other stations.

Fig. 5
figure 5

The GEV distribution for extreme temperature in Gavar station

Full size image

In the following, distribution parameters were obtained using the DE-MC method (for Gavra station, Fig. 6). According to the white dashed line in this figure, the non-stationary behavior of maximum temperature can be expressed by parameters of \({\upmu }_{0 }=32.38\), \({\upmu }_{1}=0.011\), scale = 0.75, and shape =  − 0.21, which were obtained by averaging 5000 iterations.

Fig. 6
figure 6

DE-MC realizations of the GEV parameters with a Bayesian analysis in Gavar station

Full size image

As evaluation criteria, scale and shape parameters do not show a non-stationary behavior, unlike the location parameter. Therefore, only the non-stationary state with respect to \(\upmu\) (location parameter) was discussed by considering a linear function model: \(\upmu \left(\mathrm{t}\right)=32.38+0.011t\). According to Table 2, convergence values were higher in the non-stationary than the stationary state, indicating non-stationary behavior in the selected station.

Table 2 The GEV distribution parameters and evaluation criteria for the selected station
Full size table

Frequency analysis of GPD distribution

First, the threshold value was estimated using the mentioned methods (for Gavar station, Fig. 7). In the first method, the threshold value is the area at which the graphs begin to linearize with a high slope. In the second method (the Hill estimator), there is a relatively large deviation from the straight line. It should be noted, as long as data above the threshold follows the GPD distribution, the threshold selection is somewhat optional (Fig. 7). The results showed that the threshold values were 35.3, 32.7, 32.3, 33, and 34.4 for Arak, Ashtian, Sarugh, Gavar, and Shanagh stations, respectively (Fig. 8). Then, the GPD distribution parameters were obtained based on the DE-MC method (Table 3).

Fig. 7
figure 7

Threshold selection by two methods: a mean residual life, b Hill plot, in Gavar station

Full size image
Fig. 8
figure 8

The GPD distribution for extreme temperature in Gavar station

Full size image
Table 3 The GPD distribution parameters and evaluation criteria for the selected station
Full size table

Frequency analysis

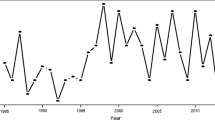
In this section, by comparing the convergence criteria, it can be said that GEV outperformed GPD in modeling extreme temperature. For instance, the convergence values in the Gavra station for both non-stationary GEV and GPD were 0.4193 and 0.3954, respectively. After detecting the GEV distribution as the best model and estimating its parameters, the values of the return level in the different return periods of 2, 10, 20, 50, and 100 years in the stationary and non-stationary state were determined. For example, in the Gavar station in the stationary state, the values of the return periods were constant and unchanged for all years, while in the non-stationary state, the temperature increases (Fig. 9).

Fig. 9
figure 9

Return periods of maximum temperature amount for stationary (a) and non-stationary (b) states in Gavar station

Full size image

As indicated in Table 4, for the 100-year return period, the average value of temperature is 37.52 °C in the stationary state, whereas in the non-stationary state, the temperature changes from 34.37 °C (1901) to 35.75 °C (2016).

Table 4 The return level of extreme temperature in the non-stationary state based on AMS
Full size table

Conclusion

Extreme temperatures as a record-breaking phenomenon have been occurred all over Iran including different climatic regions. In this county, a positive trend in annual maximum temperature (AMT) has been occurred during recent decades which causes a non-stationary (NS) conditions in its extreme temperatures. The main objective of this study was to compare extreme value theory (EVT) methods in the non-stationary analysis of maximum temperature in Arak plain. To achieve this purpose, the maximum temperature was collected from the CRU gridded dataset for the selected stations of the study area during 1901–2016. Time series of maximum temperature were extracted using two methods of block maxima (BM) and peaks-over-threshold (POT). The results showed that the monthly temperature data extracted from the CRU climate database have good accuracy and validity for the region. Hence, the results of MK, ADF, KPSS, and Petit statistical tests showed that the maximum annual temperature of the selected stations has a trend and is non-stationary and heterogeneous. Threshold selection methods (MRL plot and Hill plot) showed no difference among the threshold values. Therefore, the mean of threshold values was used as a selected threshold to extract time series. Moreover, the comparison of convergence evaluation criteria for the annual maximum temperature time series using AMS sampling was more accurate than the POT sampling method. Regarding the convergence criteria for the AMS approach, Arak and Shanagh stations were more non-stationary than other stations. A comparison of the maximum annual temperature values in stationary and non-stationary states in different return periods showed that the maximum temperature difference is about 0.8 °C in the short return period (2 years). Finally, the findings in this study indicate that the consideration of non-stationarity in extreme temperature time series is a necessity during return level estimations over the study area. Also, we recommend that for nonstationary, extreme value modeling is employd exogenous covariates such as large-scale climate modes and hydrological variables.