Introduction

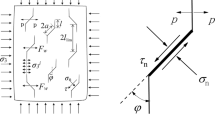
To understand the inelastic behavior of rock material subjected to stresses, it is necessary to study the underlying microscale nonlinear deformation mechanisms (Golshani et al., 2006; Zhao et al., 2016; Yuan et al., 2013; Paliwal & Ramesh, 2008; Wang et al., 2020; Lin et al., 2019; Cao et al., 2016a; Zhao et al., 2017a; Wang et al., 2019a; Xie et al., 2020; Lin et al., 2015; Zhao et al., 2018). The rock nonlinear mechanical behaviors are related with the cracking and propagation of rock crack under static compression (Lin et al., 2016; Cao et al., 2016b; Zhao et al., 2020a; Wang & Wan, 2019), unloading (Zhou, 2005), dynamic loads (Zhou et al., 2008; Zhou & Yang, 2018; Zhou & Yang, 2007; Zhou, 2006; Zhou et al., 2004), and rotation of principal stress axes (Zhou, 2010). A frictional sliding crack model giving rise to tensile microcrack represents one major micromechanism of inelastic behavior of rock material (Ashby & Hallam, 1986; Ashby & Sammis, 1990; Horii & Nemat-Nasser, 1985; Steif, 1984; Baud et al., 1996; Lehner & Kachanov, 1996; Wang et al., 2000; Zhao et al., 2019a; Kemeny & Cook, 1986). As shown in Fig. 1, the frictional sliding crack model consists of a sliding shear crack (main crack) and wing cracks that emerge symmetrically from both ends of the sliding shear crack. When shear stress induced by far-field stresses on the crack surface overcomes frictional force, the crack surface would slide over each other causing stress concentration on the tip of the crack, finally leading to the initiation and splitting propagation of wing crack.

Fig. 1
figure 1

A sketch of frictional sliding crack (a) subjected to far-field stresses only and (b) the combination of far-field stresses and hydraulic pressure

Full size image

The various approximate solutions to stress intensity factor (SIF) at the wing crack tip have been developed by many scholars in the last several decades (Horii & Nemat-Nasser, 1985; Steif, 1984; Baud et al., 1996; Lehner & Kachanov, 1996; Wang et al., 2000; Zhao et al., 2019a). The proposed models comprehensively considered many factors, such as the direction of main crack surface, orientation of the wing crack propagation, lateral stress and friction coefficient of the main crack surface, and so on. It is noted that to simplify matters, the proposed wing crack models did not consider the interaction among cracks and the hydraulic pressure in cracks are rarely taken into account. The existence of hydraulic pressure in the main crack decreases the effective normal stress on the main crack surface, promoting the sliding of the main crack. Moreover, the hydraulic pressure which is applied on wing crack face as a face force exacerbates wing crack propagation, with water flowing into wing cracks once the wing crack initiates and propagates (Horii & Nemat-Nasser, 1985; Lehner & Kachanov, 1996).

To clarify the effect of the hydraulic pressure on crack propagation, many researchers have studied the initiation and propagation mechanism of rock cracks experimentally and theoretically, when a hydraulic pressure is applied (Bruno Gonçalves & Einstein, 2018; Liu et al., 2014; Teufel & Clark, 1984; Zoback et al., 1977; Zhao et al., 2019b; Zhao et al., 2017b; Wang et al., 2019b; Zhao et al., 2019c; Zhou & Bi, 2018; Zhao et al., 2020b). The findings demonstrate that the peak strength and coalescence patterns of specimens with hydraulic pressure in cracks differ remarkably from those without hydraulic pressure due to a promoting effect of hydraulic pressure on crack propagation. Even though these studies provided useful information regarding the fracturing mechanisms of rock cracks subject to hydraulic pressure, the evolution laws of stress intensity factor (SIF) at the crack tip subjected to hydraulic pressure have still not elucidated clearly. This article attempts to study the evolution laws of SIF at the wing crack tip subjected to hydraulic pressure and far-field stresses, theoretically and numerically, based on the previous wing crack models proposed, and further enhances the understanding of the mechanical behavior of hydraulic fracturing. However, although this article only considers the case of a single crack, six theoretical models of wing cracks are all studied. The next important step in our approach will be to introduce crack interactions and to analyze their effects on the solution that we have proposed in this article.

Previous wing crack model proposed

For a frictional sliding crack, as frictional force applied on the main crack face is overcome by shear stress induced by far-field stresses σ1 andσ3, the main crack surface would slide over each other, with a tensile stress concentration at the tip of the main crack leading to the initiation and propagation of wing crack at the tip of the main crack, as shown in Fig. 1a. The solutions to stress intensity factor (SIF) at the tip of wing crack, based on various approximations, have been developed by a number of scholars (Horii & Nemat-Nasser, 1985; Steif, 1984; Baud et al., 1996; Lehner & Kachanov, 1996; Wang et al., 2000; Zhao et al., 2019a):

(1) The model of Horii and Nemat-Nasser (HN model) (Horii & Nemat-Nasser, 1985): The entire configuration is replaced by a single straight crack inclined to the axis of compression at an angle θ between the main crack and the straight winged crack, and the straight crack is loaded by a pair of point forces collinear with the direction of the initial crack. H. Horii and S. Nemat-Nasser (Horii & Nemat-Nasser, 1985) proposed an approximate formula for the SIF KI at the tip of the wing crack:

$$ {\mathrm{K}}_{\mathrm{I}}=\frac{2a{\tau}_{eff}\sin \uptheta}{\sqrt{\pi \left(l+l\ast \right)}}-{\sigma_n}^{\prime}\sqrt{\pi l} $$
(1)
$$ \left\{\begin{array}{l}{\sigma_n}^{\prime }=\frac{1}{2}\left[\left(\sigma 1+\sigma 3\right)+\left(\sigma 1-\sigma 3\right)\cos 2\left(\upbeta +\uptheta \right)\right]\\ {}{\tau}_{eff}=\frac{1}{2}\left({\sigma}_1-{\sigma}_3\right)\sin 2\upbeta -\frac{\mu }{2}\left[\left(\sigma 1+\sigma 3\right)+\left(\sigma 1-\sigma 3\right)\cos 2\upbeta \right]\end{array}\right. $$
(2)

where a is half of the crack length, β is the main crack inclination angle, l is the wing crack propagation length, l* is the equivalent crack length, l* = 0.27a, τeff is the effective shear stress applied on main crack face, \( {\sigma}_n^{\hbox{'}} \) is the normal stress applied on the wing crack, μ is the friction coefficient of the main crack surface, θ is the orientation of straight wing crack against the main crack, and σ1 and σ3 are the maximum and minimum principal stresses, respectively.

(2) The model of Steif (S model) (Steif, 1984): Steif simplified the wing crack into a straight crack with a length of 2 l and assumed that the middle of the crack was subjected to the relative slip displacement of the initial main crack, and the corresponding KI calculation formula was derived (S model):

$$ {K}_{\mathrm{I}}=\frac{3}{4}\sqrt{\frac{\pi }{2}}{\tau}_{eff}\left(\sin \frac{\uptheta}{2}+\sin \frac{3\uptheta}{2}\right)\left(\sqrt{2a+l}-\sqrt{l}\right)-{\sigma_n}^{\prime}\sqrt{\frac{\pi l}{2}} $$
(3)

(3) The model of Baud et al. (B model) (Baud et al., 1996): Baud et al. proposed the approximate SIF solution at the wing crack tip by introducing the equivalent length leq of the wing crack:

$$ {\displaystyle \begin{array}{l}{K}_{\mathrm{I}}=3{\tau}_{eff}\sqrt{\frac{a+{l}_{eq}}{\pi }}\arcsin \left(\frac{a}{a+{l}_{eq}}\right)\sin \uptheta \cos \frac{\uptheta}{2}-{\sigma_n}^{\prime}\sqrt{\pi l}\\ {}{l}_{eq}=\frac{9}{4}l{\cos}^2\frac{\uptheta}{2}\end{array}} $$
(4)

(4) The model of Lehner and Kachanov (LK model) (Lehner & Kachanov, 1996): Lehner and Kachanov put forward an approximate calculation formula of KI, which has the proper asymptotic behavior for both long and short wing cracks:

$$ {K}_{\mathrm{I}}=\frac{2a{\tau}_{eff}\cos \upbeta}{\sqrt{\pi \left(l+\frac{3a\cos^2\upbeta}{\pi^2}\right)}}-{\sigma_n}^{\prime}\sqrt{\pi l} $$
(5)

(5) The model of Wang et al. (W model) (Wang et al., 2000): Wang et al. analyzed and compared the accuracy of different wing crack models and proposed an improved analytical model:

$$ {K}_{\mathrm{I}}=2{\tau}_{eff}\sin \uptheta \left[\frac{3}{2}{e}^{-\frac{l}{a}}\cos \frac{\uptheta}{2}+\left(1-{e}^{-\frac{l}{a}}\right)\right]\cdotp \left[\sqrt{\frac{a+l}{\pi }}\cdotp \arcsin \left(\frac{a}{a+l}\right)-\sqrt{l}\right]-{\sigma_n}^{\prime}\sqrt{\pi l} $$
(6)

(6) The model of Zhao et al. (Z model) (Zhao et al., 2019a): Zhao et al. proposed an improved wing crack model based on the model of Baud et al. to cover the whole range from extremely short to very long wing crack lengths:

$$ {\displaystyle \begin{array}{l}{K}_{\mathrm{I}}=3{\tau}_{eff}\sqrt{\frac{a+{l}_{eq}}{\pi }}\arcsin \left(\frac{a}{a+{l}_{eq}}\right)\sin \uptheta \cos \frac{\uptheta}{2}-{\sigma_n}^{\prime}\sqrt{\pi l}\\ {}{l}_{eq}=\left[\frac{0.667}{\cos^2\left(0.5\uptheta \right)}-1\right]{ae}^{-\frac{l}{a}}+\frac{9}{4}l{\cos}^2\frac{\theta }{2}\left(1-{e}^{-\frac{l}{a}}\right)\end{array}} $$
(7)

By summary, these six theoretical models are based on two different assumptions: (1) the stress-driven wing crack and (2) the displacement-driven wing crack. In order to better compare and understand the existing work, the characteristics of the six theoretical models involved in this article are summarized as follows are listed in Table 1.

Table 1 Comparison of various theoretical models (Horii & Nemat-Nasser, 1985; Steif, 1984; Baud et al., 1996; Lehner & Kachanov, 1996; Wang et al., 2000; Zhao et al., 2019a)
Full size table

Theoretical and numerical models of wing crack subjected to hydraulic pressure and far-field stresses

Theoretical model

The hydraulic pressure in the main crack can reduce the effective shear driving stress, and the hydraulic pressure in wing crack can decrease the normal stress applied on wing crack, which is the force opposing wing propagation. To study the SIF at the wing crack tip subjected to hydraulic pressure and far-field stresses, it is necessary to revise the previous wing crack model proposed without considering hydraulic pressure. The following hypotheses were put forward (Fig. 1b):

(1) For rough rock cracks, a coefficient α which characterizes the connected area against the total area is introduced. So the effective hydraulic pressure normally applied on the main crack is αp (see Fig. 1b).

(2) The hydraulic pressure p as a distributed force is applied on the wing crack surface (see Fig. 1b).

The effect of hydraulic pressure p on the SIF at the wing crack tip can be accounted for, when the τeff and \( {\sigma}_n^{\hbox{'}} \) in Eqs. 1 ~ 7 are replaced by τpeff and \( {\sigma}_{pn}^{\hbox{'}} \):

$$ \left\{\begin{array}{l}{\sigma_{pn}}^{\prime }=\frac{1}{2}\left[\left(\sigma 1+\sigma 3\right)+\left(\sigma 1-\sigma 3\right)\cos 2\left(\upbeta +\uptheta \right)\right]-p\\ {}{\tau}_{peff}=\frac{1}{2}\left({\sigma}_1-{\sigma}_3\right)\sin 2\upbeta -\frac{\mu }{2}\left[\left(\sigma 1+\sigma 3\right)+\left(\sigma 1-\sigma 3\right)\cos 2\upbeta -\alpha p\right]\end{array}\right. $$
(8)

The different theoretical models of wing crack subjected to hydraulic pressure and far-field stresses can be proposed by replacing τeff and \( {\sigma}_n^{\hbox{'}} \) in the HN, S, B, LK, W, and Z models by τpeff and \( {\sigma}_{pn}^{\hbox{'}} \).

Numerical solution method for the SIF at wing crack tip

A numerical model of wing crack subjected to hydraulic pressure and far-field stresses is proposed by ANSYS based on finite element model (FEM). Singular element in ANSYS is arranged in the first row elements that surround the wing crack tip (Fig. 2b). Generally when the radius of the singular element is less than 1/8 of the crack length, the calculation result of the SIF at the crack tip is accurate and can meet the accuracy requirements. In this article, it takes as 1/10 of the wing crack length. A series of nodes along the crack face in the vicinity of the crack tip is chosen to calculate their relative opening displacements Δw(r) (Fig. 2a). Moreover, contact element satisfying the Mohr-Coulomb criteria is used to simulate the sliding of the main crack.

Fig. 2
figure 2

Wing crack tip: (a) local cylindrical coordinate system and distribution of nodes along crack face in the vicinity of the crack tip and (b) singular elements surrounding the wing crack tip

Full size image

The numerical methods commonly employed for calculating SIFs are of two types: (1) displacement matching methods, such as extrapolation methods; and (2) energy-based methods, such as the crack closure integral method, the J-integral technique (Chen et al., 2020), and so on. The displacement extrapolation method is among the most commonly used methods. In this article, SIFs for the crack propagation problem are calculated through linear elastic analysis using the displacement extrapolation method. In this method, the displacement of node pairs on the crack edges is applied to compute the SIFs at the crack tip. The method depends on the size of elements around the crack tip field and requires the use of refined mesh to produce more accurate numerical results.

The opening displacement w(r) near a crack for linear elastic materials at plane stress condition yields:

$$ w(r)=\frac{K_{\mathrm{I}}(r)}{4G}\sqrt{\frac{r}{2\pi }}\left[\left(2k-1\right)\sin \frac{\theta }{2}-\sin \frac{3\theta }{2}\right]-\frac{K_{\mathrm{I}\mathrm{I}}(r)}{4G}\sqrt{\frac{r}{2\pi }}\left[\left(2k+3\right)\cos \frac{\theta }{2}+\cos \frac{3\theta }{2}\right]+0(r) $$
(9)

where r, θ are the radius vector and polar angle in a local cylindrical coordinate system, respectively, as shown in Fig. 2a; G and ν are the shear modulus and Poisson’s ratio of material, respectively; 0(r) presents the terms of order r or higher; KΙ(r) and KΙΙ(r) are mode Ι and II SIFs near the wing crack tip, respectively, and \( k=\frac{3v}{1+v} \) for the plane strain condition.

Equation 9 at θ = ± 180.0° and dropping the higher order terms yields:

$$ w(r)=+\frac{K_{\mathrm{I}}(r)}{2G}\sqrt{\frac{r}{2\pi }}\left(1+k\right) $$
(10)

The KΙ(r) of nodes near the wing crack tip can be calculated according to relative opening displacement:

$$ {K}_{\mathrm{I}}(r)=\sqrt{2\pi}\frac{G}{1+k}\frac{\left|\Delta w(r)\right|}{\sqrt{r}}=\sqrt{2\pi}\frac{2G}{1+k}\frac{\left|w(r)\right|}{\sqrt{r}} $$
(11)

Let r → 0, the SIF KI at the tip of wing crack can be obtained:

$$ {K}_{\mathrm{I}}=\underset{r\to 0}{\lim}\sqrt{2\pi}\frac{2G}{1+k}\frac{\left|w(r)\right|}{\sqrt{r}} $$
(12)

The KI at the wing crack tip can be calculated by the numerical simulation of ANSYS as follows:

(1) Determinate the nodal displacements w(r) along crack face in the vicinity of the crack tip (see Fig. 2a).

(2) Determinate the KΙ(r) of nodes in the vicinity of the crack tip according to Eq. 11.

(3) Determinate the KI at the wing crack tip by a linear fitting. The KΙ(r) of nodes can be fitted with a straight line as follows:

$$ {K}_{\mathrm{I}}(r)= Br+A $$
(13)

Let r = 0, the approximate solution to the KI at the wing crack tip can be obtained by numerical analysis:

$$ {K}_{\mathrm{I}}=A $$
(14)

Numerical simulation

A rock plate with a width of 80 cm and a height of 160 cm, containing a central inclined crack, was used as the calculation example. The 9921 nodes and 3247 triangle elements are in the model. The calculation parameters of rock crack are given: 2a=\( \sqrt{2} \)cm, θ = π/4, μ = 0.3, and α = 0.6. A uniform far-field stress σ1 is applied on top of the model while lateral stress σ3 = λσ1 is applied on both sides. Hydraulic pressures αp and p are applied to the inner surface of the main crack and wing cracks, respectively. Axial compressive stress σ1 = 25 MPa, combined with different lateral stresses σ3=− 2.5 MPa (λ = − 0.1), 0 (λ = 0), and 2.5 MPa (λ = 0.1) and different hydraulic pressures p = 0, 1 MPa, 3 MPa, and 5 MPa, are analyzed to study the effect of lateral stress and hydraulic pressure on the SIF at the wing crack tip. Supposing that the wing crack propagates approximately at the direction parallel to the maximum principal stress, a fairly small angle between the wing crack and axial stress of π/25 is set, with an angle θ between the wing crack and main crack of π/4 + π/25. The wing crack numerical model and grid meshing considering the combined action of hydraulic pressure and far-field stresses are shown in Fig. 3.

Fig. 3
figure 3

The FEM of wing crack and application of hydraulic pressure

Full size image

Figure 4a, b, and c shows the dimensionless SIFKI (\( \overline{K_{\mathrm{I}}}={K}_{\mathrm{I}}/{\sigma}_1\sqrt{\pi a} \)) at the wing crack tip versus the equivalent crack propagation length L(L = l/a) at various lateral stresses and hydraulic pressures, based on FEM simulation. It can be clearly seen that the dimensionless SIF at the wing crack tip is affected by the lateral stresses and hydraulic pressures at a certain axial stress. The results from numerical simulation indicate that the curves of the dimensionless SIF‾KI at the wing crack tip versus the equivalent crack propagation length L are in three major types (Fig. 4d):

Fig. 4
figure 4

The dimensionless SIF ‾KI (‾KI = \( {K}_{\mathrm{I}}/{\sigma}_1\sqrt{\pi a} \)) at the wing crack tip versus the equivalent crack propagation length L(L = l/a) at lateral stresses of (a) 2.5 MPa, (b) 0, and (c) −2.5 MPa and the (d) three types of ‾KI–L curve, based on FEM analysis

Full size image

(1) Drop type (D type): The dimensionless SIF‾KI monotonously drops with an increase in equivalent crack propagation length L, i.e., \( \frac{\partial \overline{K_{\mathrm{I}}}}{\partial L}<0 \), which is considered a general rule as reported by previous studies (Horii & Nemat-Nasser, 1985; Steif, 1984; Baud et al., 1996; Lehner & Kachanov, 1996; Wang et al., 2000).

(2) Drop then rising type (DR type): The dimensionless SIF‾KI firstly drops and then rises with an increase in equivalent crack propagation length L, i.e., \( \frac{\partial \overline{K_{\mathrm{I}}}}{\partial L}<0 \), in an extremely short range of wing crack length, and then \( \frac{\partial \overline{K_{\mathrm{I}}}}{\partial L}>0 \) in a relatively long range of wing crack.

(3) Rising type (R type): The dimensionless SIF‾KI keeps the rising trend with an increase in equivalent crack propagation length L, i.e., \( \frac{\partial \overline{K_{\mathrm{I}}}}{\partial L}>0 \).

A horizontal straight line \( \overline{K_I}={K}_{IC}/{\sigma}_1\sqrt{\pi a} \) is added in Fig. 4d. It is noted that the‾KI–L curve lying above the horizontal straight line indicates the wing crack propagates due to the SIF at the wing crack tip greater than KIC, whereas the‾KI–L curve lying below the horizontal straight line indicates the wing crack fails to propagate.

The D type curve exhibits two conditions: the whole KI–L curve lies below the above horizontal straight line, which implies that there is no cracking at the main crack tip, or the KI–L curve intersects the above horizontal straight line at Point B, where an equivalent crack propagation length of LC can be obtained (see Fig. 4d). The D type curve indicates that the SIF at the wing crack tip decreases during the propagation process of wing crack and the wing crack propagation ends once the SIF drops to fracture toughness KIC of rock. So the D type curve exhibits a steady propagation behavior of wing crack. Generally, Both DR and R type curves lying above the horizontal straight line imply that there is an unsteady propagation behavior of wing crack due to the stage where an increasing SIF at the wing crack tip occurs during wing crack propagates.

The D type curve gradually transfers to the DR and R type curves with increasing hydraulic pressure. For the lateral stress σ3=2.5 MPa, the‾KI–L curve is the D type at hydraulic pressures of 0, 1 MPa, and 3 MPa; however, the DR type is at hydraulic pressure of 5 MPa, respectively. For the lateral stress σ3=0, the ‾KI–L curve is the D type at hydraulic pressures of 0, 1 MPa; however, the DR type is at the hydraulic pressures of 3 and 5 MPa, respectively. For the lateral stress σ3=− 2.5, the‾KI–L curve is the DR type at the hydraulic pressures of 0, 1, and 3 MPa; however, the R type is at the hydraulic pressure of 5 MPa, respectively.

The evolution laws of minimum principal stress in the vicinity of the crack tip during wing crack propagation affect the type of‾KI–L curve. The tensile stress concentration zone with extreme high stress gradient occurs near the wing crack tip as shown in Fig. 5.

Fig. 5
figure 5

The distribution of minimum principal stress in the vicinity of the crack tip subjected to σ1 = 25 MPa, and σ3 = 0 for (a) L = 1.0 and (b) L = 2.0 at p = 0, corresponding to points 1 and 2 in Fig. 4b, and (c) L = 1.0, and (d) L = 5.0 at p = 5.0, corresponding to points 3 and 4 in Fig. 4b

Full size image

For D type curve, the tensile stress concentration zone near the wing crack tip decreases with wing crack propagation, leading to a crack arrest when wing crack propagates to a certain critical length. Figure 5a and b shows the comparison between minimum principal stress in the vicinity of the crack tip for L = 1.0 and L = 2.0 subjected to σ1 = 25 MPa, σ3 = 0, and p = 0, which indicates a remarkable decrease in tensile stress concentration zone near the wing crack tip with an increase in wing crack length. The dimensionless SIFs‾KI at L = 1.0 and L = 2.0 are 0.129 and 0.102, corresponding to points 1 and 2 in Fig. 4b, respectively. So for D type curve, the decrease of tensile stress concentration near the wing crack tip leads to a decrease in the SIF with the wing crack propagation.

For R type curve, the tensile stress concentration zone near the wing crack tip always keeps increasing with an increase in wing crack length, leading to crack propagation unsteadily. Figure 5c and d shows the comparison between minimum principal stress in the vicinity of the crack tip for L = 1.0 and L = 5.0 subjected to σ1 = 25 MPa, σ3 = 0, and p = 5 MPa. It is noted that differing from zero hydraulic pressure, the tensile stress concentration zone near the wing crack tip increases with wing crack propagation under a relative high hydraulic pressure of 5 MPa. The dimensionless SIFs‾KI at L = 1.0 and L = 5.0 are 0.384 and 0.545, corresponding to points 3 and 4 in Fig. 4b, respectively. So for R type curve, the increase of tensile stress concentration near the wing crack tip leads to an increase in the SIF with the wing crack propagation.

Comparisons between numerical simulation and theoretical model

Comparisons between numerical simulation and theoretical model are shown in Figs. 6, 7, and 8. On the whole, the tendency of theoretical model curves is in agreement with that of numerical simulation curves. The values of the sum of squared residuals (SSR) between all theoretical solutions and FEM solutions are shown in Fig. 9.

Fig. 6
figure 6

Comparisons between (a) HN model, (b) S model, (c) B model, (d) LK model, (e) W model, (f) Z model, and FEM solutions subjected to σ1 = 25 MPa and σ3 = 2.5 MPa at various hydraulic pressures

Full size image
Fig. 7
figure 7

Comparisons between (a) HN model, (b) S model, (c) B model, (d) LK model, (e) W model, (f) Z model, and FEM solutions subjected to σ1 = 25 MPa and σ3 = 0 at various hydraulic pressures

Full size image
Fig. 8
figure 8

Comparisons between (a) HN model, (b) S model, (c) B model, (d) LK model, (e) W model, (f) Z model, and FEM solutions subjected to σ1 = 25 MPa and σ3 = -2.5 MPa at various hydraulic pressures

Full size image
Fig. 9
figure 9

Residual sum of square (SSR) between all theoretical and FEM solutions subjected to (a) σ1 = 25 MPa and σ3 = 2.5 MPa, (b) σ1 = 25 MPa and σ3 = 0, and (c) (a) σ1 = 25 MPa and σ3 = − 2.5 MPa

Full size image

By comparing the tendency of theoretical curve and numerical simulation curve, it is found that the SIF obtained from the theoretical model is commonly lower than that from all numerical simulations at the hydraulic pressures of 3 and 5 MPa.

The SSRs for all theoretical solutions range from 0.0038 to 0.033 under σ1 = 25 MPa and σ3=2.5 MPa. The SSR tends to increase with an increase in hydraulic pressure with a maximum SSR at the hydraulic pressure of 5 MPa, except for the S model. The SSRs for all theoretical solutions fall between 0.0016 and 0.078under σ1 = 25 MPa and σ3=0; moreover, the SSR of theoretical solutions has the maximum value at the hydraulic pressure of 5 MPa, except for the Z model. Under σ1 = 25 MPa and σ3= − 2.5 MPa, the SSRs for all theoretical solutions range from 0.001 to 0.14.The SSR of all theoretical solutions has a relative great value at the hydraulic pressure of 5 MPa. The average SSRs of the HN, S, B, LK, W, and Z model are 0.0079, 0.0348, 0.0099, 0.0127, 0.0077, and 0.0068, respectively. So the average SSRs of the Z model and S model are the lowest and highest among all theoretical models, respectively. The Z model solution subjected to the combined action of hydraulic pressure and far-field stresses can be considered an optimal solution due to the lowest average SSR. It is noted that the fact that the results of the revised theoretical model and the numerical model are similar further reflects the correctness of the revised theoretical model. And the revised theoretical model can supply the theoretical references for the damage-fracture coupling analysis of fractured rock mass under high hydraulic pressure.

Conclusions

This article comparatively studied the evolution laws of SIF at the wing crack tip subjected to hydraulic pressure and far-field stresses, theoretically and numerically, and further enhanced the understanding of the mechanical behavior of hydraulic fracturing. Based on the study, the following conclusions can be drawn:

  1. (1)

    The revised wing crack models subjected to hydraulic pressure and far-field stresses are proposed, based on previous proposed wing crack models without considering hydraulic pressure.

  2. (2)

    Numerical simulation for the SIF at wing crack tip based on FEM indicates that the curves of the dimensionless SIF at the wing crack tip versus equivalent crack propagation length are in three major types: Drop type (D type), drop then rising type (DR type), and rising type (R type). D type curve exhibits a steady propagation behavior of wing crack; however, DR type and R type curves exhibit an unsteady propagation behavior of wing crack.

  3. (3)

    The tendency of theoretical model curves is in agreement with that of numerical simulation curves. The average SSRs of the Z model and S model are the lowest and highest among all theoretical models, respectively. The Z model solution subjected to the combined action of hydraulic pressure and far-field stresses can be considered an optimal solution.