Introduction

In GPS real-time applications, the obtained range from the satellite to the receiver is different from the true geometric range because of various provenance of blunders (Ghilani and Wolf 2014). The ionosphere causes a defer, which is a negative for phase observations and positive for the code ones due to the total electron content (TEC) along the path from the GPS satellite to the receiver (Hofmann-Wellenhof et al. 2008). This postponement is viewed as the most fantastic provenance of all blunders that influence the GPS signals (Bhattacharya et al. 2008).

Moreover, the Sun plays a vital role in the magnitude of this error because the high solar activity that increases the amount of refraction induced by the ionosphere (Sickle 2015). A high energy wave known as solar wind is generated by the Sun. The solar wind reacts with the geomagnetic field, and occasionally, these charged particles rise significantly due to the solar flares on the surface of the Sun (Klobuchar 1991). Many particles arise in the atmosphere of the Sun, which is known as CMEs (coronal mass ejections). Many of such CMEs will significantly distort the Earth’s magnetic field and induce a geomagnetic storm (Sidorov et al. 2019). Such storms that occur in northern auroral regions in particular and last many hours may often reach the middle and equatorial latitudes, disrupt the ionosphere, and degrade the performance of the GPS receiver (Sedeek et al. 2017; Elghazouly et al. 2019b; Elsayed et al. 2018).

The GPS signals travel from the space to the Erath passing through the ionosphere so that GPS signals considered as a sensor to estimate ionospheric delay. Although there are different agencies that provide global maps for ionospheric error in means of VTEC (vertical total electron content), these VTEC values over Egypt are interpolated because there is no IGS (International GNSS Service) GPS station over Egypt; so, the IEE MATLAB program developed to address GPS signals to estimate the ionospheric delay from a real data over Egypt.

The ionosphere products produced by the IGS analysis center uses pseudo-range observables to estimate the ionospheric error because pseudo-range is free of an ambiguous term; so, it is easy to estimate ionosphere errors. As the phase observables are more accurate than the pseudo-range, a common approach is to smooth pseudo-range with the phase observables. The smoothed phase observables by pseudo-range eliminate noise and avoid addressing ambiguities directly (Xiang et al. 2017).

Since the consistency of estimated ionosphere errors depends mainly on the used observables, two approaches were considered in this contribution to compare and estimate ionospheric blunders using phase observables; the first one is using the linear combination to fix the ambiguity term after repairing cycle slips, the second approach smoothing pseudo-range with phase observables to avoid fixing ambiguity.

The objective of this contribution is to study remotely sensed ionospheric error using smoothed and unsmoothed phase observables during high and low geomagnetic activity over Egypt.

The following sections are the applied mathematical algorithms, case study, results, and conclusion.

Ionosphere error estimation techniques

In this contribution, the geometric range between the receiver, satellite, and other frequency-independent errors was eliminated by combining phase (L1–L2) and pseudo-range (P1–P2) from GPS measurements. Ionosphere biases were estimated using phase observables by two different models, which were explained in the next section.

Melbourne-Wübbena linear combination of double-band phase and code observables utilized for distinguishing and repairing cycle slips in this current contribution. The cycle slip term ΔN1(k) − ΔN2(k) when k is the epoch number can be estimated as (e.g., Dengynu et al. 2012; Elghazouly et al. 2019a):

$$ {\Delta N}_1(k)-{\Delta N}_2(k)={N}_{\mathrm{WL}}\left(k-1\right)-{N}_{\mathrm{WL}}(k) $$
(1)

Estimating ionosphere biases using phase observables

Fixing the ambiguities is essential to estimate ionospheric biases. In this model, phase observables were used without any smoothing (unsmoothed). The mathematical algorithm can be explicated as (e.g., Leandro 2009)

$$ {L}_{\mathrm{GF}}={L}_1-{L}_2=\left(1-\upgamma \right)\mathrm{MF}\left(I+{\nabla}_{\Phi}\left({\Phi}_{\mathrm{P}}-{\Phi}_0\right)+{\nabla}_{\uplambda}\left({\lambda}_{\mathrm{P}}-{\lambda}_0\right)\right)+ Nb{\prime}_{\mathrm{gf}} $$
(2)

where LGF is the geometry-free carrier-phase observation in length units, MF is the ionosphere mapping function expressed as Eq. (8), I is the vertical ionospheric delay at the station position, ∇Φ and ∇λ are the latitudinal and longitudinal gradients, respectively, ΦP and λP are the geodetic latitude and longitude of the ionospheric piercing point, Φ0 and λ0 are the geodetic latitude and longitude of the station, γ is the factor to convert the ionospheric delay from L1 to L2 frequency, unitless and Nb′gf is the ambiguity parameter which includes the carrier-phase integer ambiguity plus a collection of biases.

In this model, a combination of dual-frequency carrier phase and code data is used to estimate the ambiguity terms after repairing cycle slips using the following form (Xu 2007)

$$ \left(\begin{array}{c}{\lambda}_1{N}_1\\ {}{\lambda}_2{N}_2\\ {}{B}_1\\ {}{C}_{\uprho}\end{array}\right)=\left(\begin{array}{c}1-2a\\ {}-2a\\ {}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$q$}\right.\\ {}a\end{array}\kern1em \begin{array}{c}-2b\\ {}2a-1\\ {}\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$q$}\right.\\ {}b\end{array}\kern1em \begin{array}{c}1\\ {}0\\ {}0\\ {}0\end{array}\kern1em \begin{array}{c}0\\ {}1\\ {}0\\ {}0\end{array}\right)\ \left(\begin{array}{c}{P}_1\\ {}{P}_2\\ {}{\lambda}_1{\Phi}_1\\ {}{\lambda}_2{\Phi}_2\end{array}\right) $$
(3)

where a is the geometry term and b is the ionosphere term, N1 and N2 are the unknown integer ambiguity of L1 and L2, respectively, P1 and P2 are the observed pseudo-range on L1 and L1, respectively, q = (1/b), and ionosphere B1 and geometry Cρ are the functions of the codes and are independent on the phases. Sequential least square adjustment (SLSA) was applied to fix the ambiguity term using Eq. (10).

Estimating ionosphere biases using smoothed phase observables

The smoothing process used historically to estimate the ionospheric biases. The following steps can be defined as the corresponding ionospheric bias estimation process.

  1. 1-

    Cycle slip repair, in this contribution, a hybrid of multi-frequency phase and code measurement is applied to eliminate the ambiguity term after fixing cycle slip to get continuous arcs according to Eq. (1).

  2. 2

    Estimating the average between phase and code for continuous arcs. The ionospheric effects are canceled, and biases are introduced as follows (e.g., Xiang et al. 2017):

$$ {L}_{\mathrm{GF}}={L}_1-{L}_2=\left(1-\upgamma \right)I+{B}_{\mathrm{I}}+{\mathrm{DPB}}_{\phi_1-{\phi}_2}^{\mathrm{s}}-{DPB}_{\phi_1-{\phi}_2}^{\mathrm{r}}+{\upvarepsilon}_{\phi } $$
(4)
$$ {P}_{\mathrm{GF}}={P}_2-{P}_1=\left(1-\upgamma \right)I+{\mathrm{DCB}}_{{\mathrm{P}}_1-{\mathrm{P}}_2}^{\mathrm{s}}-{\mathrm{DCB}}_{{\mathrm{P}}_1-{\mathrm{P}}_2}^{\mathrm{r}}+{\varepsilon}_{\mathrm{P}} $$
(5)

where LGF and PGF are the phase and code measurement geometry free, I is the L1 ionosphere blunder at GPS receiver location, γ is the factor to convert the ionospheric delay from L1 to L2 frequency, BI = λ1N1 − λ2N2 is the ionosphere ambiguity variable, DPB is the differential phase biases (where subscription s for satellite and r for the receiver), DCB is the differential code biases (where subscription s for satellite and r for the receiver), εϕ, εP other unmodeled errors in phase and code measurement.

$$ {\left({L}_4-{P}_4\right)}_{\mathrm{arc}}=\frac{1}{n}{\sum}_1^n{\left({L}_4-{P}_4\right)}_{\mathrm{i}}=\left({B}_I+{\mathrm{DPB}}_{\phi_1-{\phi}_2}^s-{\mathrm{DPB}}_{\phi_1-{\phi}_2}^r\right)-{\mathrm{DCB}}_{P_1-{P}_2}^s+{\mathrm{DCB}}_{P_1-{P}_2}^r+{\left({\varepsilon}_{\mathrm{P}}\right)}_{\mathrm{arc}} $$
(6)
  1. 3-

    Eliminating ambiguity term as follows:

$$ {L}_{\mathrm{smoothed}}={L}_4-{\left({L}_4-{P}_4\right)}_{\mathrm{arc}}=\left(1-\upgamma \right)\mathrm{MF}(I)+\left({\mathrm{DCB}}_{P_1-{P}_2}^s-{\mathrm{DCB}}_{P_1-{P}_2}^r\right)+\left({\varepsilon}_{\mathrm{P}}\right)+{\varepsilon}_{\mathrm{L}} $$
(7)

In this model, \( {\mathrm{DCB}}_{P_1-{P}_2}^r \) and \( {\mathrm{DCB}}_{P_1-{P}_2}^s \) are estimated using the zero difference DCB estimation (ZDDCBE) code published by Sedeek et al. (2017)

The main advantages of a smooth code can be seen in reducing noise and in avoiding the direct resolution of ambiguities. However, the biggest challenge is to level errors.

Mapping function (MF) is used as a basis of a spherical ionosphere single layer model, which is computed according to, e.g., Leandro et al. (2010):

$$ \mathrm{MF}=\sqrt{1-{\left(\ \left(\frac{r}{\left(r+ sh\right)}\right)\cos (e)\ \right)}^2} $$
(8)

where r is the radius of Earth, 푠ℎ is the ionosphere shell height, β is the angle of elevation of the satellite at the shell height piercing point, and e is the elevation angle of the satellite at receiver as seen in Fig. 1.

Fig. 1
figure 1

Elements of the ionospheric shell model (Hofmann-Wellenhof et al. 2008)

Full size image

The ionosphere blunder estimation is executed using SLSA expressed as (Xu 2007)

$$ L= AX $$
(9)
$$ X={\left({A}_1^{\mathrm{T}}\times {W}_1\times {A}_1+{A}_2^{\mathrm{T}}\times {W}_2\times {A}_2\right)}^{-1}\left({A}_1^{\mathrm{T}}\times {W}_1\times {l}_1+{A}_2^{\mathrm{T}}\times {W}_2\times {l}_2\right) $$
(10)

where 퐴1 and 퐴2 are the design matrix of the first and the second groups of observations, respectively, 푊1 and 푊2 are the weight matrices of the first and the second groups of observations, respectively, l1 and l2 are the observation vectors of the first and the second group, respectively, and is the anonymous parameter vector.

These models were handled in MATLAB® and were named IEE. Figure 2 demonstrates the block diagram of the ionosphere error computation using the IEE program.

Fig. 2
figure 2

Block diagram of the IEE program

Full size image

Case study

In this contribution, Kp, Ap indices, and the G-scale were utilized to investigate the origins and effects of the worldwide magnetic activity. The planetary K-index is taken into account as a superb indication for irregularities within the magnetic field of the Earth. It varies between 0 and 9, where a value of 0 is minimal, and 9 indicates a severe geomagnetic storm. The National Oceanic and Atmospheric Administration (NOAA) uses a five-level G-scale to denote the intensity of the geomagnetic activity detected and predicted. This scale varies from G0 to G5; G0 is the lowest and G5 the highest (Du et al. 2010). G-level and its correspondence Kp value appear in Table 1.

Table 1 G-scale and Kp index according to NOAA (https://www.noaa.gov)
Full size table

In this contribution, the IEE program was applied to compute the ionosphere blunder using smoothed and unsmoothed phase observables for six ground-based multi-frequency GPS receivers, using observations based on days of quiet conditions (no geomagnetic storms). These stations, which are located over Egypt, are called Marsa-ALAM, ASWAN, BORG-ELARAB, MANSOURA, MATROUH, and PORT-SAID, as appeared in Fig. 3. Then, the IEE program was applied again on the same six stations using observations based on days with high geomagnetic storms.

Fig. 3
figure 3

Distribution of GNSS receivers over Egypt

Full size image

Quiet and stormy days in this investigation were indicated using tesis.lebedev.ru/, which presents the values of Kp, Ap indices, and G-scale that are given in Table 2.

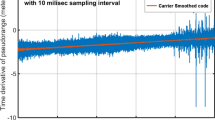
Table 2 The geomagnetic storm activity during days of study (http://tesis.lebedev.ru/en/magnetic_storms.html/)
Full size table

To investigate the influence of the geomagnetic storms on ionosphere blunder, the consequences of stormy and quiet days compared. The next figures (Figs. 4, 5, 6, 7, 8, and 9) show the estimated ionosphere blunder values of the stations, using smoothed and unsmoothed phase observations, in various geomagnetic conditions and the distinction between them. These differences describe the influence of the geomagnetic storms on ionosphere blunder.

Fig. 4
figure 4

Errors caused by the ionosphere at ALAM GPS station during stormy days (a) and quiet days (b)

Full size image
Fig. 5
figure 5

Errors caused by the ionosphere at BORG GPS station during stormy days (a) and quiet days (b)

Full size image
Fig. 6
figure 6

Errors caused by the ionosphere at MANS GPS station during stormy days (a) and quiet days (b)

Full size image
Fig. 7
figure 7

Errors caused by the ionosphere at MTRH GPS station during stormy days (a) and quiet days (b)

Full size image
Fig. 8
figure 8

Errors caused by the ionosphere at SAID GPS station during stormy days (a) and quiet days (b)

Full size image
Fig. 9
figure 9

Errors caused by the ionosphere at ASWN GPS station during stormy days (a) and quiet days (b)

Full size image

Results

The influence of geomagnetic storms on the computed ionosphere can be noted after using the IEE program on the stations mentioned above. Figures 4, 5, 6, 7, 8, and 9 show a comparison between the estimated ionosphere blunder using smoothed and unsmoothed phase observables during various geomagnetic conditions, according to indices of Kp, Ap, and G-scale, which were provided by tesis.lebedev.ru/. Each figure of them describes the ability of geomagnetic storms in disturbing the computed ionosphere blunder.

Table 3 shows mean ionosphere error (MIE) and standard deviation of mean (SDM) for several DOY through stormy and quiet days using unsmoothed and smoothed phase observation, where the red text is the highest value and the blue one is the lowest value at each station. The consequences of the mean and standard deviations of the mean for estimated ionosphere error throughout days of stormy conditions extend between 23 (at ASWN) and 6 cm (at SAID) using the unsmoothed phase model and between 21 (at ALAM) and 8 cm (at MANS) using the smoothed phase model. Otherwise, the SDM for the estimated ionosphere error throughout quiet conditions extends between 17 (at MTRH) and 5 cm (at MANS) using the unsmoothed phase model and between 16 (at BORG) and 3 cm (MANS) at using the smoothed phase model.

Table 3 The estimated mean ionosphere error and standard deviation of the mean for GPS stations over Egypt using observations based on days of stormy and quiet conditions
Full size table

As shown in Figs. 4, 5, 6, 7, 8, and 9, eliminating ambiguity term using the smoothed phase model provides results much smoother than unsmoothed phase results. I think this is because of the fixed ambiguity over the continuous arc, as solar flare increases in mid of the day the ionosphere error increase.

Geomagnetic activity plays an essential role in disturbing the ionospheric blunders. The highest estimated ionospheric error using the unsmoothed model is 13.19 m in a stormy day at low latitude station (ASWN) (see Fig. 9a) (DOY51; 2014), and the highest estimated ionospheric error using the smoothed model is 13.34 m in a stormy day at low latitude station (ALAM) (see Fig. 4a) (DOY52; 2014).

Figures 10 and 11 show mean ionosphere errors and the standard deviations (SD) for stormy and quiet day of year (DOY) estimated by the proposed models.

Fig. 10
figure 10

Mean ionosphere error and standard deviations at ALAM, ASWN, and BORG GPS stations for stormy days (a) and quiet days (b)

Full size image
Fig. 11
figure 11

Mean ionosphere error and standard deviations at MANS, MTRH, and SAID GPS stations for stormy days (a) and quiet days (b)

Full size image

From analyzing the results of two models, a relatively high MIE and SD over six GPS stations can be noticed in stormy days (see Figs. 10a and 11a) and a significant decrease in MIE and SD in quiet days (see Figs. 10b and 11b).

The ionospheric error residuals are the difference between the ionospheric error from unsmoothed and smoothed phase observables. Figures 12 and 13 demonstrate the ionosphere error residuals at each GPS receivers over Egypt for 3 quiet days and 3 stormy days, except Aswan ionosphere error residuals for 2 quiet days and 2 stormy days. As seen in Figs. 12 and 13, geomagnetic activity has a significant effect on estimating ionospheric blunders. The highest residual was 9.15 m at a low latitude location (ALAM) in stormy condition, and the minimal residual was 0.84 m at SAID station in the quiet condition. The higher ionospheric error ranges observed at three GPS stations (ALAM (low latitude), ASWN (low latitude), and MANS (mid-latitude)) all were in stormy days, while the lower ranges (ALAM (low latitude), SAID (Mid-latitude), and MANS (Mid-latitude)) all were in quiet days.

Fig. 12
figure 12

Ionosphere residuals over three GPS stations (ALAM, ASWN, BORG) for stormy and quiet days

Full size image
Fig. 13
figure 13

Ionosphere residuals of three GPS stations (MANS, MTRH, SAID) for stormy and quiet days

Full size image

Also, residuals around the mean were estimated for both models; the maximum and minimal difference using the unsmoothed phase model was 13 m at ASWN station in a stormy day and 1.02 m at SAID station in a quiet day, respectively. While the maximum and minimal differences using the smoothed phase model were 6 m at ALAM station in a stormy condition and 0.67 m at MANS station in a stormy condition, respectively. The smoothed phase observables demonstrate the lowest difference around the mean in the stormy and quiet days. The summary of these investigations explained in the conclusion.

Conclusions

In this paper, the ionospheric delay acquired from fixing ambiguity using a linear combination of pseudo-range and phase observables (unsmoothed phase) and carrier phase smoothed code method (smoothed phase) to avoid addressing ambiguity bias directly. After result analysis, these conclusions can be derived:

  • the ionospheric blunders from the smoothed phase model much smoother compared with the unsmoothed phase model, due to eliminating ambiguity term by smoothing phase observation.

  • The ionosphere blunder relies upon the magnetic activity as the error increases with the increase of Kp and Ap indices.

  • The geomagnetic storms increased the estimated ionospheric error using the unsmoothed and smoothed phase model by about 200% as in ASWN and by about 265% as in SAID, respectively.

  • The geomagnetic storms increase the SDM of the estimated ionospheric error using the unsmoothed and smoothed phase model by about 180% as in MANS and by about 350% as in SAID, respectively.

  • Ionosphere error relies upon the station latitude where the ionospheric error increases and can be a real problem in equatorial and high-latitude regions as ASWAN and ALAM stations.

Finally, the contrast between the stormy and quiet ionosphere errors clarifies the necessity of estimating the ionosphere blunders when considering GPS observations to improve the precision of point positioning, especially throughout stormy days. For further works, using other modes for fixing ambiguity, and converting the estimated ionosphere bias from smoothed and unsmoothed phase models into VTEC and investigating its effect on point positioning.