Introduction

Since indefinite sliding displacement indicates common destruction factors for evaluating the seismic stability of slopes, the evaluation of this parameter has been taken into consideration by researchers in order to design stable soil structures in the past few decades. To assess seismic deformation, the analysis of a rigid sliding block is convenient while the sliding mass is approximately rigid and shallow (Newmark, 1965). In this case, the response of the slope can be ignored because the natural period of sliding mass (Ts) is essentially zero. Thus, the input time history of acceleration can be used to measure the displacement by double-integrating it or, alternatively, seismic loading parameters, such as peak ground acceleration (PGA), can be utilized to predict sliding displacement from empirical models. However, flexible sliding masses make inappropriate the analysis of sliding block when the natural periods are greater than zero and it is important to consider the dynamic response of such cases. The dynamic response of sliding mass is calculated by decoupled analysis without considering sliding displacement and then, the dynamic responses are used to analyze the sliding deformation, as reported by Makdisi and Seed (1978) and Bray and Rathje (1998). In this analysis, the horizontal equivalent acceleration time history (HEA, k) is obtained by double-integration of the input acceleration time history. Alternatively, maximum horizontal equivalent acceleration (Kmax) is utilized in empirical models instead of PGA in order to evaluate the seismic displacement.

In general, the variation of soil properties must be recognized in continuum even within homogeneous soils. However, most geotechnical analyses have been performed by deterministic models considering the single realization (mean values) of soil parameters applied to numerical models (e.g., Kuriqi et al., 2016; Tavasoli and Ghazavi, 2018). This simplification leads to increasing uncertainties. In fact, one of the common sources of discrepancy between the estimated and the actual performance of any geotechnical system is the variability of the soil parameters (Phoon and Kulhawy, 1999). There are some parameters which represent spatial variability of soil properties including coefficient of variation (CoV) introduced by mean value and variance, auto-correlation length (θ), and probability distribution. In recent years, spatial variability of soil properties and randomness of soil behavior have received considerable attention. Several geotechnical and geological studies have been carried out to provide detailed information on the spatial distribution of soil characteristics for geotechnical and structural designs (e.g., Muceku et al., 2015, 2016). Griffiths et al. (2002) have studied the effect of spatial variability of undrained shear strength of soil on bearing capacity of rough rigid strip foundations and the pile bearing capacity under horizontal load considering the heterogeneity of this parameter of soil has been analyzed by Haldar and Babu (2008) with considering Monte Carlo simulation (MCS) to generate random fields. In addition, the effect of coefficient of variation of soil undrained shear strength and auto-correlation length on soil system bearing capacity was interpreted.

A large number of researches have analyzed the effect of spatial variability of soil properties on slope stability such as Hicks and Samy (2002), Griffiths and Fenton (2004), Low et al. (2007), Griffiths et al. (2009), Li et al. (2014), Jiang et al. (2014), Jamshidi Chenari and Alaie (2015), but only a few of those researches have been carried out in the field of stochastically seismic analyses considering the heterogeneity of soil characteristics in order to recognize the seismic response of soil deposits and slopes. Nadi et al. (2014, 2016, 2019) outlined the uncertainty in assessing the seismic slope stability and co-seismic landslide deformations arising from random behavior of soil properties. Moreover, seismically induced soil dynamic responses and liquefaction have been studied by Popescu et al. (1997, 2005), Koutsourelakis et al. (2002), Lizarraga and Lai (2014). Nevertheless, considering that seismic response of sliding mass (i.e., k history), it is related to shear wave velocity (Vs) varying inherently in the space, investigating the effect of spatial variability of shear wave velocity on MHEA had required decreasing uncertainty in evaluating seismic deformations based on the decoupled analysis.

In this paper, the effect of spatial variability of shear wave velocity on the dynamic response of sliding mass and earthquake-induced deformations in soil slopes is investigated. The maximum horizontal equivalent acceleration (kmax) and seismically induced deformations were evaluated in both stochastic and deterministic manners and the results were compared to have insight into the influence of random heterogeneity of shear wave velocity. The stationary random fields of low-strain shear modulus were generated using the auto-correlation matrix decomposition method, along with Monte Carlo Simulation and the effects of the coefficient of variation of shear modulus (CoVG0), and auto-correlation length (θ) on kmax was studied. Subsequently, the decoupled deformations were computed using an analytical solution.

Methodology

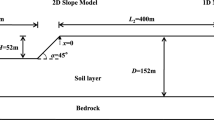
In this section, a typical slope model having height H = 20 m and inclination i = 30° was considered in all dynamic analyses, as shown in Fig. 1. The density ρ = 2000 (kg/m3) and Poisson’s ratio ν = 0.3 were assigned to the soil and the Mohr-Coulomb failure criterion with c = 35 kPa and ϕ = 25◦ was allocated to the soil. To consider the model mesh, the lateral boundary conditions have moved away from the region of interest to decrease and minimize the effect of reflected waves on slope response. According to Rizzitano et al. (2010), the results’ accuracy is not affected by the thickness D of the half-space, whether the length L is sufficiently considered to make a geometrical attenuation of the seismic waves. A length L equal to 4H was assumed to be adequate and a thickness D = 20 m was considered as well. It is also advantageous to apply free field boundary conditions to decrease the effect of artificial wave reflection.

Fig. 1
figure 1

Two-dimensional finite difference model

Full size image

The maximum size of elements was determined to avoid filtration of high-frequency components of the input seismic motion during the propagation process and ensure the accuracy of the numerical solution, so that Eq. (1) proposed by Kuhlemeyer and Lysmer (1973) was satisfied.

$$ \varDelta l\le \frac{V_{\mathrm{s}}}{10{f}_{\mathrm{max}}} $$
(1)

where Δl is the maximum length of elements and fmax is the highest frequency of the input motion. Square elements having length Δl=2 m were considered adequate according to Eq. (1). The attenuation of the energy was defined in the model through the hysteresis damping generated by Mohr-Coulomb constitutive law. Furthermore, Rayleigh damping was used to remove high-frequency noise. Rayleigh damping matrix was considered a combination of the mass and stiffness matrices by the coefficients α and β depending on the critical damping ratio and oscillation frequency. Although this formulation includes a frequency-dependent damping, a correct selection of the two frequencies allows ensuring a constant damping in the range of natural frequencies of the slope. Specifying the natural frequency of slope, the Rayleigh damping coefficients α and β were selected. The power spectra of velocity response resulted from elastic undamped analysis at the crest of the slope was interpreted to achieve this purpose. Since the major portion of energy was damped by hysteresis damping, only a slight critical damping ratio ζ = 0.5% was assumed for Rayleigh damping.

In this study, six significant earthquake records having different characteristics that occurred in the north and east of Iran were designated, as observed in Table 1. Peak ground accelerations (PGA) ranged from 0.085 to 0.531 g, mean periods (Tm) range was from 0.137 to 0.785 s, as reported by Rathje et al. (1998), and effective durations varied from 4 to 25 s. Baseline correction was performed for all records. Since the frequency contents of records did not exceed 15 Hz, there was no need to filter them. It was worth to note that there was a limitation for selecting more earthquake motion records as the seismic stochastic analysis was significantly time-consuming. It is important to mention that more investigation on the influence of earthquake characteristics on mean Kmax is necessary and that these parameters play a significant role in assessing the dynamic response of slopes. For this reason, a range of input motions with various characteristics have been used for dynamic analyses of this study. These earthquake shaking records were selected based on their peak ground acceleration PGA, mean period Tm, magnitude M, and effective duration which are the most crucial parameters in dynamic analyses. Nonetheless, the random behavior of the earthquake has not been further investigated since the primary focus of this study is to investigate the uncertainty in evaluating the seismic response of slopes due to the random heterogeneity of shear wave velocity of the soil. Also, the earthquake records were selected in a way to include a wide range of aforementioned earthquake characteristics to have insight into the dynamic response of slopes under various seismic loading conditions. Moreover, the selected earthquakes have resulted in severe losses in different areas and analyzing the dynamic response of slopes under the action of these ground shakings is of interest.

Table 1 Characteristics of input motions in this study
Full size table

Pseudo-static analysis based on the strength reduction method was carried out to determine the critical slip surface geometry and the yield acceleration, Ky, i.e., seismic coefficient corresponding to the safety factor of one which represents minimum acceleration required to initiate sliding mass failure. At the beginning of the analysis, horizontal acceleration was increased until the safety factor reached one and the failure just started to happen. Then, to determine the slip surface geometry, the x/y coordinates of locations in which maximum shear strain increment (SSI) was within some percentage of the peak strain value were specified. Afterward, slip surface geometry was obtained by fitting a circular arc to the points having aforementioned x/y coordinates using the least squares method, and yield acceleration (Ky) equal to 0.55 was obtained from the pseudo-static analysis. The equivalent horizontal acceleration was evaluated by computing average response acceleration time history on the critical slip surface. The time history of acceleration for each earthquake record was specified in 12 locations on the slip surface and the average acceleration time history was obtained using Eq. (2) and programming with FLAC software to perform this calculation.

$$ k(t)=\frac{\sum \limits_{i=1}^n\mathrm{HE}{\mathrm{A}}_i(t).{m}_i}{\sum \limits_{i=1}^n{m}_i} $$
(2)

where k(t) is the equivalent horizontal acceleration at time t on slip surface, ki(t) is the equivalent horizontal acceleration at the point i of the sliding surface, and mi is the mass of the material column located above point i. The maximum k(t) was selected as kmax.

To evaluate the seismic slope deformation based on decoupled analysis, the horizontal equivalent acceleration (HEA) (K) time history was first computed. Then, seismic displacement is given by double-integrating this time history. Rathje and Antonakos (2011) have suggested Eq. (3), as the valuable model in terms of Kmax (MHEA) to estimate seismic displacement without the need for integrating process, which parameters a1 to a7 were summarized in Table 2, where D is the seismic displacement in centimeters and M is the earthquake magnitude. The natural period of sliding mass (Ts) used in Eq. (3) was determined by Eq. (5) suggested by Makdisi and Seed (1978), where y is the maximum thickness of sliding mass and Vs is soil shear wave velocity.

Table 2 Parameters of Eq. (3) by Rathje and Antonakos (2011)
Full size table
$$ Ln(D)={a}_1+{a}_2\left(\frac{K_y}{K_{\mathrm{max}}}\right)+{a}_3{\left(\frac{K_y}{K_{\mathrm{max}}}\right)}^2+{a}_4{\left(\frac{K_y}{K_{\mathrm{max}}}\right)}^3+{a}_5{\left(\frac{K_y}{K_{\mathrm{max}}}\right)}^4+{a}_6\mathit{\ln}\left({K}_{\mathrm{max}}\right)+{a}_7\left(M-6\right)+{f}_1\left({T}_{\mathrm{s}}\right) $$
(3)
$$ {f}_1\left({T}_{\mathrm{s}}\right)=\left\{\begin{array}{c}3.69\bullet {T}_{\mathrm{s}}-1.22\bullet {T}_{\mathrm{s}}^2,\kern0.5em {T}_{\mathrm{s}}\le 1.5\mathrm{s}\\ {}2.78,\kern9.75em {T}_{\mathrm{s}}>1.5\mathrm{s}\end{array}\right. $$
(4)
$$ {T}_{\mathrm{s}}=\frac{4y}{V_{\mathrm{s}}} $$
(5)

Most soils are naturally formed in different depositional situations, so that their properties vary inherently from point to point. This inherent spatial variability can be observed even in homogenous soils and it is one of the major uncertainties in the geotechnical analysis. In situ properties might change horizontally and vertically for the variability of culprits, as explained by Jones et al. (2002), including depositional environments, the degree of weathering, and physical environment. The relatively simple model can represent the spatial variation of soil parameters (Phoon and Kulhawy, 1999).

$$ \xi (z)=t(z)+w(z)+e(z) $$
(6)

where ξ represents the in situ soil property, t is the deterministic trend component, w is the random component, e is the measurement error, and z is the depth. The trend and random components are illustrated in Fig. 2. A common approach to deal with the uncertainties arising from spatial variability and randomness of the soil is layering and zoning the soil deposit based on their physical and mechanical properties and assigning the mean values of soil properties to each layer. Nonetheless, in stochastic analysis, this randomness of the soil is directly outlined using stochastic approaches such as random field generation. Therefore, a one-layer slope was considered and one random field was mapped to the grid of each slope model.

Fig. 2
figure 2

Inherent variability of soil properties (Phoon and Kulhawy, 1999)

Full size image

Since it is not possible to assign shear wave velocity (Vs) directly to the soil model in finite difference code, the soil shear modulus was considered a random variable and assumed to be a log-normally distributed value represented by parameters mean μG0, standard deviation σG0, and spatial auto-correlation distance (θ) to represent the variability of shear wave velocity in this study. The desired random field is considered to be stationary; that is, the mean value and standard deviation of shear modulus are constant in depth. Use of log-normal distribution is appropriate as the soil shear modulus is non-negative and this type of distribution prevents random variables from possessing negative values. A log-normal distributed random field is given by Eq. (7).

$$ {G}_0\left(\tilde{x}_{i}\right)=\exp \left\{{\mu}_{\mathit{\ln}{\mathrm{G}}_0}\left(\overset{\sim }{x}\right)+{\sigma}_{\mathit{\ln}{\mathrm{G}}_0}\left(\overset{\sim }{x}\right){G}_i\left(\overset{\sim }{x}\right)\right\} $$
(7)

where \( \overset{\sim }{x} \) is the spatial position at which G0 is required; G\( \left(\overset{\sim }{x}\right) \) is a standard normally distributed random field with zero mean and unit variance. The values of μlnG0 and σlnG0 are determined using log-normal distribution transformations given by Eq. (8) and Eq. (9). In order to normalize the input, the shear modulus variability was expressed in terms of the coefficient of variation of shear modulus (CoVG0 = σG0/μG0).

$$ {\sigma}_{\mathit{\ln}{\mathrm{G}}_0}^2=\mathit{\ln}\left(1+\frac{\sigma_{{\mathrm{G}}_0}^2}{\mu_{{\mathrm{G}}_0}^2}\right)=\mathit{\ln}\left(1+\mathrm{Co}{\mathrm{V}}_{{\mathrm{G}}_0}^2\right) $$
(8)
$$ {\mu}_{\mathit{\ln}{\mathrm{G}}_0}=\mathit{\ln}{\mathrm{G}}_0-\frac{1}{2}{\sigma}_{\mathit{\ln}{\mathrm{G}}_0}^2 $$
(9)

To generate standard random field G\( \left(\overset{\sim }{x}\right), \) the auto-correlation matrix was created first utilizing auto-correlation function. Griffiths and Fenton (2007) have indicated that the correlation coefficient between log-normal distributed geotechnical parameters at two points follows the Gauss-Markov model and the exponential dissipation function of separation distance. Hence, in this study, the auto-correlation function is considered to be exponentially dissipating given by Eq. (10).

$$ {\rho}_{{\mathrm{G}}_0}\left(\tau \right)=\exp \left(-\frac{2\tau }{\theta}\right) $$
(10)
$$ \tau =\mid {\overset{\sim }{x}}_1-{\overset{\sim }{x}}_2\mid $$
(11)

where τ is the absolute distance between two points called separation distance and θ is the auto-correlation length. The auto-correlation length describes the distance over which the spatially random values will tend to be correlated in the random field. Thus, a large value has implied a smoothly varying field, while a small value has implied a ragged field. In this study, for simplicity, vertical and horizontal auto-correlation lengths were assumed to be equal. In other words, the generated random fields are isotropic. To create the auto-correlation matrix, separation distance (τ) was defined by the distance between the center of each element and others. The separation distance between elements directions was \( \sqrt{{\left(2 dx\right)}^2+d{y}^2} \), where dx and dy are distances between grids in x and y direction. The auto-correlation matrix was decomposed into a lower triangular one along with its transpose by Cholesky decomposition,

$$ \rho ={LL}^T $$
(12)

Given the matrix L, the correlated standard normal random field is obtained as follows:

$$ {G}_i=\sum \limits_{j=1}^i{L}_{ij}{Z}_j\kern1.25em i=1,2,\dots .n $$
(13)

where Zj is the sequence of independent standard normal random variables. Log-normally distributed random field was generated by Eq. (6) using Gi.

For this research, the computational process was conducted by developing a MATLAB function that generated two-dimensional random fields based on each set of stochastic input variables summarized in Table 3, so that stochastic input variables were selected based on the information in the literature. Mean shear modulus (μG0) was adopted based on mean shear wave velocity Vs = 400 m/s. Results were calculated in terms of dimensionless auto-correlation length given by θ/H ranging from 0.2 to 0.8 related to θ from 4 to 16 m, where H was the height of the slope. Resulting random fields were mapped to FLAC mesh by a subroutine in FISH code. Figure 3 illustrates the flowchart for statistical numerical analysis.

Table 3 Ranges of stochastic parameters for the spatial variability of shear modulus
Full size table
Fig. 3
figure 3

Flowchart for statistical numerical analysis

Full size image

Two generated random fields of shear modulus for CoVG0 = 30% and θ/H = 0.2, 0.8 were illustrated in Fig. 4. It could be observed that for θ/H = 0.2, shear modulus changed rapidly from element to element and the generated random field was ragged. As θ/H increases to 0.8, the random field became smoother and more homogenous. It could be noted that with increasing θ, the auto-correlation between adjacent elements have increased.

Fig. 4
figure 4

Generated random fields for shear modulus with CoVG0 = 30%. a θ/H = 0.2. b θ/H = 0.8

Full size image

For each set of statistic parameters given by CoVG0 and θ, Monte Carlo simulation was performed and N realizations of parameters were generated for each value of PGA. The stability of results was analyzed according to the number of realizations. The statistical fluctuation of mean and coefficient of variation of kmax was assessed by means of Monte Carlo simulation. Figure 5 indicates the results based on 1000 realization of shear modulus for earthquake record No. 1, CoVG0 = 12%, and θ/H = 0.2. As observed, the fluctuation of both mean and coefficient of variation of kmax has occurred within a tolerable range after 500 realizations. Therefore, N = 500 was considered adequate and acceptable in this study.

Fig. 5
figure 5

Fluctuation of a mean kmax and b coefficient of variation of kmax

Full size image

Results and discussion

Two probabilistic parameters CoVG0 and θ had vital physical effects on the nature of a random field as shown in Fig. 4. The influence of these two parameters on the maximum horizontal equivalent acceleration (Kmax) and the variation of Kmax coefficient has been illustrated in Fig. 6 for earthquake record No. 2. The mean maximum horizontal equivalent acceleration (mean Kmax) was compared with its deterministic value for CoVG0 = 12% and 30%, and the different ratios of θ/H equal to 0.2, 0.4, and 0.8. The deterministic Kmax was calculated as 1.444 m/s2 through seismic response analysis considering constant shear modulus. Mean Kmax in the most variable condition with CoVG0 = 30% and θ/H = 0.2 is equal to 1.395 m/s2, which was only slightly less than the deterministic value. It was concluded that there was not a significant difference between mean Kmax and its deterministic value for slopes subjected to motions having low intensity even when CoVG0 increased up to 30%. The reason for this phenomenon was that the elements with lower shear wave velocity have neutralized the effect of elements with higher shear wave velocity, so that average response acceleration along the slip surface approximately is equal to its deterministic value. Thus, in these circumstances, the spatial variability of shear wave velocity can be neglected. As θ/H increased, the spatial variability of shear wave velocity became smoother. Therefore, mean Kmax achieved closer to deterministic Kmax.

Fig. 6
figure 6

Effect of CoVG0 and θ/H on a mean kmax and b coefficient of variation of kmax for earthquake record No. 2

Full size image

With increasing CoVG0, the CoV of Kmax increased. The Kmax coefficient of variation was greater in higher values of θ/H, since in higher values of θ/H the mean Kmax tended to its deterministic value; on the other hand, the shear modulus varied up to 30% of the mean. This high variation of the shear modulus and the approximate equality of mean Kmax with the deterministic Kmax led to the increment of the Kmax coefficient of variation. In other words, the more the mean Kmax tended to the deterministic Kmax, the more the coefficient of variation of Kmax increased.

Figure 7 indicates the variation of mean Kmax and the variation of Kmax coefficient with CoVG0 and θ/H for earthquake record No. 5 in which deterministic Kmax of 8.93 m/s2 was calculated from seismic response analysis. It was observed that the mean Kmax for CoVG0 = 30% was lower than the value obtained for CoVG0 = 12%. A mean value of Kmax equal to 8.67 m/s2 was interpreted for CoVG0 = 12% and θ/H = 0.2 whereas for the same auto-correlation length, the mean Kmax became 8.29 m/s2 if CoVG0 = 30%. As a result, the mean Kmax decreased more with increasing the CoVG0. The difference between mean Kmax and deterministic value for earthquake record No. 5 was considerably greater and more intense than earthquake record No. 2. As an illustration, mean Kmax was 7.17% less than deterministic Kmax in CoVG0 = 30% and θ/H = 0.2 which was the most variable condition. It represented that the spatial variability of shear wave velocity could have a vital influence on Kmax for slopes subjected to strong motions especially when this variability was drastic and must be taken into account in computing sliding mass response. The value of mean Kmax slightly increased as θ/H became greater. It could be explained that when auto-correlation length rises, the spatial variability of shear wave velocity was smoother and Kmax mean became closer to its deterministic value. As similar to what is observed in Fig. 6, the Kmax coefficient has increased with the increase of CoVG0 for record No. 5. However, its value was lower in comparison with the value obtained for earthquake record No. 2. The main reason was that for slip surface subjected to earthquake record No. 5, the discrepancy between the mean Kmax and the deterministic Kmax was more in comparison with one subjected to earthquake record No. 2. It means that the mean Kmax contributes more to the variation of shear modulus, declining the contribution of Kmax the coefficient variation. The greater variation of Kmax coefficient was interpreted in higher values of θ/H, because of the same reason remarked and described before.

Fig. 7
figure 7

Effect of CoVG0 and θ/H on a mean kmax and b coefficient of variation of kmax for earthquake record No. 5

Full size image

Earthquake characteristics have a crucial effect on the seismic slope response. One of the most important parameters for estimating earthquake intensity was the peak ground acceleration (PGA). Figure 8 demonstrates the maximum horizontal equivalent acceleration factor (i.e., normalized mean Kmax by deterministic Kmax) represented by (Kmax)s/(Kmax)d versus PGA, where (Kmax)s was the mean maximum horizontal equivalent acceleration and (Kmax)d was its deterministic value. As shown in Fig. 8, the maximum horizontal equivalent acceleration factor of earthquake record No. 5 had the most difference between mean Kmax and deterministic value occurred for this earthquake with high PGA (i.e., 4.42 m/s2), as mentioned before. For sliding mass subjected to earthquake record No. 6 having higher PGA than earthquake record No. 5 (i.e., 5.21 m/s2), the maximum horizontal equivalent acceleration was very close to one. It means that although this earthquake has higher PGA, there was a slight discrepancy between mean Kmax and its related deterministic value. As a result, PGA was not the only earthquake character influencing the stochastic maximum horizontal equivalent acceleration. As the main reason, it could be told that the earthquake behavior was totally random and it was not usually possible to describe an earthquake with only one intensity measure. Hence, more investigations have required comprehending the influence of earthquake characteristics on the stochastic mean maximum horizontal equivalent acceleration (mean Kmax) which was not the main subject of this paper and it can be the background of future research.

Fig. 8
figure 8

Effect of PGA on kmax factor

Full size image

As previously observed, the mean Kmax is equal to 7.17% and it was less than the deterministic Kmax for earthquake record No. 5, CoVG0 = 30% and θ/H = 0.2 which was the most variable situation. Also, to obtain more clarity on how this discrepancy caused by spatial variability of shear wave velocity influences deformations resulted from the decoupled analysis, seismic deformations related to the mentioned maximum horizontal equivalent accelerations were computed by Eq. (3) and compared with each other. For this purpose, the natural period of sliding mass (Ts) must be evaluated using Eq. (4). Considering the maximum thickness of the sliding mass of 11.075 m has resulted from the pseudo-static analysis, and shear wave velocity Vs was 400 m/s, the natural period of sliding mass was obtained as 0.11075 s. For earthquake record No. 5, CoVG0 = 30% and θ/H = 0.2, the decoupled seismic deformation related to the mean Kmax (i.e., 8.29 m/s2) was 1.572 cm, whereas the seismic deformation is equal to 2.41 cm considering deterministic Kmax (i.e., 8.93 m/s2) which was greater more than 52%. Therefore, it could be concluded that the spatial variability of shear wave velocity had a considerable effect on decoupled seismic deformations for slopes subjected to intense motions. Generally, the behavior of earthquakes is highly random and fairly unknown in spite of several deterministic and probabilistic studies conducted to have a better insight into the characteristics of the ground shakings. Moreover, the spatial variability of shear wave velocity leads to increasing uncertainties in evaluating the response of buildings and geotechnical structures. For the stated reasons, there are uncertainties to make a general conclusion about the physical reason for this complicated phenomenon. Therefore, further investigations are required in this field. According to deterministic analyses, deamplification of ground motion could occur at high PGAs due to higher levels of produced damping (energy dissipation) in the soil medium compared with that under earthquake loads with lower PGAs, especially for the slopes with greater natural periods. The presence of the soil elements with higher shear wave velocities close to those with lower values of shear wave velocity in heterogeneous soil slopes could result in lower natural periods and consequently, greater maximum horizontal equivalent acceleration. This increase could be more pronounced for high PGAs since the amplification of response acceleration due to spatial variability of shear wave velocity neutralizes the deamplification of ground motion arising from high values of PGA.

Conclusions

The present study has discussed the effect of spatial variability of shear wave velocity on the seismic response of sliding mass as well as on seismic deformations resulted from the decoupled analysis using FLAC software based on finite difference method and programming with MATLAB. The effects of the coefficient of shear modulus variation (CoVG0) and auto-correlation length (θ), as two important probabilistic parameters, have been investigated by generating random fields. The results have demonstrated that:

  • For slopes subjected to the earthquakes with low intensity, the spatial variability of shear wave velocity varying within the range of statistical parameters considered in this study might not have an important effect on the seismic response of sliding mass.

  • The difference between mean Kmax and deterministic Kmax increased with increasing the coefficient of shear wave velocity variation and decreasing with increasing of auto-correlation length for slopes subjected to intense motions.

  • The difference between stochastic and deterministic kmax led to the considerable discrepancy between the corresponding seismic deformations resulted from the decoupled analysis. This discrepancy was more evident for earthquake record No. 5 where stochastic deformation was almost 52% of the deterministic one.

Generally, more researches considering the slopes subjected to a wide range of earthquake records having different characteristics are also recommended in order to investigate the effect of earthquake characteristics on the mean maximum horizontal equivalent acceleration.