Introduction

Variation of ground temperature with respect to time and depth from the surface is a natural phenomenon that had been of scientific interest since the seventeenth century (Buntebarth 2002). Ground temperature has a major effect on physical and chemical properties of the earth landscape, and it is an important factor in pedogenesis (Jenny 1941). As a matter of fact, the ground temperature recorded at 50 cm below the soil surface (generally referred to as ground surface temperature regime) is a key factor for the classification of the earth surface at the sub-order class (USDA 2010). Heat flow and ground thermal properties have direct effect on the well-being of people because of its applications on food, housing, and other parts of living. Various researchers had shown that ground temperatures present significant fluctuation on both daily and annual basis (Penrod et al. 1960; Carson 1963; Mihalakakou et al. 2002). Heat flow inside the earth is influenced by several parameters such as solar radiation, air temperature, wind speed, time of the year, shading, and soil properties that present a seasonal or irregular variation (Michael 2008). Evolution of physical and economic developments has encouraged the presence of artificial impervious surfaces, which, in turn, affect the ground temperatures.

Landsberg and Blanc (1958) established that the range of ground temperature at different depths and the diffusivity of soil are associated with values of density, conductivity, and specific heat of soils. Researchers have conducted subsurface temperature measurements under bare ground surfaces (Fluker 1958) and under covered surfaces (Penrod et al. 1960; Liu et al. 2016). Gupta et al. (1982) reported that in addition to an annual cycle, ground temperature undergoes daily cycle, which correlates with changes in the weather. These variations were reported to be limited in the near-surface region: daily cycles infiltrated to about 0.5 m and weather cycles infiltrated to a depth of about 1.0 m below the surface.

In early literatures (Carson 1963; Van Wijk and De Vries 1963; Gold 1964; Krishnan and Kushwaha 1972; Ghuman and Lal 1982; Cenis 1989), ground temperature of the uniform earth surface was determined as a solution of the Fourier heat diffusion equation with a constant thermal diffusivity in a semi-infinite medium under periodical forcing at the near-surface region. Ground heat transfer has been proved to be influenced by a complex combination of conductive and porous convective processes (Passerat de Silans et al. 1996). The combination has brought the solutions of the thermal conduction–convection equation. Shao et al. (1998) correlated analytical results from data obtained during a field infiltration experiment with the natural temperature variations. The results showed that the estimated temperatures were in agreement with the direct measurements.

Gao et al. (2003) solved the equation for one-dimensional ground thermal conduction–convection by applying the harmonic method analytically. The study contributed significantly to developments in predictions of ground temperature distribution and water flux density. Heusinkveld et al. (2004) used the method of harmonic analysis, with thermal conduction alone to evaluate subsurface temperature. This was done in a sandy desert belt located in the northwest of Negev, Israel.

Most investigations of subsurface temperatures are derived from the principles of heat flow and energy balance (Parton 1984; Stathers et al. 1985; Nobel and Geller 1987; Thunholm 1990; Campbell 1997). Subsurface temperatures at various depths are unique parameters that are useful in describing the surface energy processes and the regional environmental and climate conditions of the area. Since ground heat conduction is a very slow process (Hillel 1980), soil heat variation of daily or weekly timescales in shallow layers near the surface is released to the atmosphere before being distributed to the deeper layers. Only persistent long-term (such as inter-annual and decadal scales) variation in surface heat budget can propagate to deep soil layers and affect temperature variations in those layers (Lachenbruch and Marshall 1986; Beltrami and Harris 2001; Beltrami 2002).

Adequate knowledge of subsurface temperature helps in determining the depth at which service pipe like cold-gas pipeline, hot-oil pipeline meant to transport liquefied petroleum gas, crude oil, and cable system should be installed for optimum performance (Neher and McGrath 1957). Projects such as design of road and airport pavements, calculation of heat losses from structures in contact with the ground, and the design and operation of heat pumps can be carried out efficiently only if the appropriate soil temperature regime is known with reasonable accuracy. Both weather and soil conditions are important factors in the agricultural decision-making process (Myers et al. 2009). Ground temperature is directly linked to the temperature of the atmosphere because the ground is a heat sink for heat flowing between the solid earth and the atmosphere.

Luo et al. (1992) identified three types of temperature models. The first models are empirical models based on statistical relationships between ground temperature at some depths and climatological and soil variables (James and Wayne 1991; Ahmad and Ghulam 2008) while the second models are mechanistic models that focus on physical processes to predict the upper boundary temperature and estimate the temperature of deeper layers with the Fourier equation (Van Bavel and Hillel 1976). Mixed empirical and mechanistic models are the third models that calculate the temperature of different soil layers based on physical principles of heat flow (Wierenga and de Wit 1970; Renáta and Nándor 2012). It was shown that the commonly used solution to the heat flow equations by Van Wijk and De Vries (1963) performed well when applied at deeper soil layer but there were errors when applied to near-surface layers where more extreme variations in temperature occur, especially if the approaches do not consider heat sources or sinks below the surface.

Fourier analysis of soil temperature is a versatile technique in studying soil heat transfer and soil properties. The resulting coefficients of soil temperature obtained by Fourier analysis depict the impartial description of the variation with depth of the soil temperature waves, which measures phase and amplitude variations of the annual and diurnal soil temperature cycles with depth. The information may be helpful in revealing configuration of heat transfer process within the study area.

Earlier works (Krishnan and Kushwaha 1972: Bocock et al. 1974: Gupta et al. 1984; Liakatas 1994) had shown that harmonic analysis technique gives good fit and accurate estimation of ground temperature. Fourier analysis breaks a series into independent constituents called harmonics (Amou et al. 2010), which depict some significant descriptions of a series. The solar radiation and air temperature govern the ground temperature by influencing the rate at which energy is transferred between the atmosphere and the ground. Solar radiation is probably the single most important factor influencing ground temperature (Williams and Gold 1976; Florides and Kalogirou 2004). However, there exist disparities in ground temperature at different depths, especially close to the surface. The local variations from regular cycles in reality are due to the changes in weather conditions, like cloudiness, precipitation, and warm and cool spells. Averaging the data over a suitable time interval can minimize these fluctuations but may not eliminate them completely, especially down through the ground profile. To reduce the fluctuation due to the effect of weather conditions, the average data may further be analyzed by subjecting it to Fourier analysis. The objective of this study is to analyze the temporal variation of ground temperature from the surface at different depths by Fourier analysis and to compute the ground thermal diffusivity using the amplitude and phase angles of the first three harmonics of the annual thermal wave.

Materials and methods

Descriptions of experimental site

Field measurements were conducted in an open field (latitude 07 08′ 15.6″ N, longitude 03 17′ 12.3″ E) in Akole, Oke-Ata, Ita-Oshin, Abeokuta, Ogun State, Nigeria. Abeokuta has a moderately hot, humid, tropical climate and is situated in the derived Savanna agro-ecological zone of Southwestern Nigeria. The soil of research location has loamy sand surface texture and sand clay loamy subsurface texture and was classified as typical hapludalf (USDA 2010).

Climate and hydrology of Abeokuta

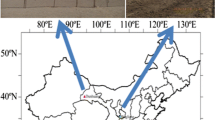
Abeokuta is located between latitude 7.09° to 7.22° N and longitude 3.30° to 3.40° E (Fig. 1) and is underlain by the basement complex rocks. It consists of gneisses, quartzite, calcilicate, biotite hornblende schist, and amphibolites as its most widespread rock formation (Rahaman and Kogbe 1976). These rocks are of Precambrian age to early Paleozoic age, and they extend from the northeastern part of Ogun State running southwestward and dipping towards the coast. The basement complex metamorphic rocks are branded by various folds, structures of various degrees of complexity, faults, and foliation (Ufoegbune et al. 2009). The common metamorphic rocks encountered are gneiss, schist, quartzite, and amphiboles. The individual rock has various hydrogeologic characteristics. The northern side of Abeokuta is characterized by pegmatite underlain by granite, while the southern part (made up of granitic gneiss) enters the transition zone with the sedimentary basin. The western part is characterized by granitic gneiss that is less porous alongside with various quartzite intrusions (Key 1992).

Fig. 1
figure 1

Map of Ogun State showing the experimental site

Full size image

The topography of Abeokuta is described by two types of landforms: sparingly distributed hillocks of granite and nearly flat landscape. The craggy rock-strewn relief is noticeable towards the north, central, and southeastern parts of the city (Ufoegbune et al. 2010). Abeokuta falls within the humid tropical region that is characterized with wet and dry seasons. The wet season usually starts in March and ends in early November, and this period is usually dominated by heavy rainfall with a short break between July and August. The dry season is experienced from late November to early March when the area is influenced by the northeasterly winds. The city has an annual average rainfall of about 1290 mm (Ajiboye et al. 2015). The monthly mean temperature ranges from 25.7 °C in July to 30.2 °C in February with the annual average temperature of 27 ± 0.5 °C. High humidity (generally above 50%) and long wet season encourage the availability of soil water and the continuous presence of moisture in the air.

Experimental field design

A ground profile measuring 1.2 m by 1.2 m in area was dug up to a depth of 2 m in the experimental site (Fig. 2). Five 5TM temperature sensors were horizontally inserted into the vertical wall of the profile at depths 2, 50, 100, 150, and 200 cm. The sensors were connected to a Decagon EM50 data logger and programmed to collect soil temperature data at intervals of 1 s. The collected data was averaged hourly and stored in the logger internal memory. The volumetric water content of the ground at the specified depths (2, 50, 100, 150, and 200 cm) was collected. Data was collected during the period starting from 1 January 2014 to 31 December 2014. The total number of soil temperature readings collected was 8760. The sensor measures temperature by an onboard thermistor. Signal filtering minimizes salinity and textural effects, making the 5TM sensors to be precise in most media (http://www.decagon.com/soils/volumetric-water-content-sensors/5tm-vwc-temp). The 5TM sensor measures temperature ranging from − 40 to + 60 °C with an accuracy of ± 1.0 °C and a resolution of 0.1 °C.

Fig. 2
figure 2

Schematic of experimental setup

Full size image

Harmonic analysis of soil temperatures

The state of energy in the soil is characterized with the value of its temperature and moisture content. It has been established that a finite number of cosine and sine relations in terms of Fourier series could be used to account for any time series that is made up of a set of data points of equal interval (Mark et al. 2001). The temperature waves travel according to a diurnal cycle, which could be described as a periodic function in a form of sinusoidal waves oscillating at about average temperature (T a).

$$ T={T}_{\mathrm{a}}+\sum_{n=1}^{N/2}\left({a}_n\cos \frac{2\pi nt}{p}+{b}_n\sin \frac{2\pi nt}{p}\right) $$
(1)

Equation (1) is known as the Fourier equation, where T is the temperature at time t and T a is the annual average temperature, while a n and b n are half-range amplitudes. N is the total number of data, p is the period, and n is the harmonic. The nth harmonic amplitude (A n ) and nth harmonic phase (φ n ) are given in Eqs. (2) and (3) as

$$ {A}_n={\left({a}_n^2+{b}_n^2\right)}^{0.5} $$
(2)
$$ {\varphi}_n=\mathrm{Arctan}\left({a}_n/{b}_n\right) $$
(3)

Thermal diffusivity of the soil

Experimental determination of thermal diffusivity of the soil is not easy in the field, but it could be estimated from amplitude ratio and phase lag by assuming thermal diffusivity within the depth considered to be constant. The soil temperature distribution is governed by the Fourier heat conduction equation.

$$ \rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right) $$
(4)

where x is the depth from surface of soil, t is the time, k is the thermal conductivity of the soil, c is the specific heat, and ρ is the particle density.

De Bano et al. (1976), Richon (1987), and Pourhashemi et al. (1999), in formulating a heat transfer model in soil, treated soil as a one-dimensional semi-finite medium. Richon assumed both one- and two-dimensional modes of heat transfer in soil and reported that the difference between heat transfers in the ground as either one- or two-dimensional was less than 3%.

Thus, heat transfer in ground expressed in Eq. (4) can be reduced to the one-dimensional Fourier field equation

$$ \rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right) $$
(5)

When the thermal properties of the ground are constant, that is thermal properties are independent of the temperature of the ground, Eq. (5) becomes

$$ \frac{\partial T}{\partial t}=\alpha \frac{\partial^2T}{\partial {x}^2} $$
(6)

where \( \alpha =\frac{k}{\rho c} \) is the thermal diffusivity.

Since the ground thermal diffusivity is assumed to be constant and to be infinitely deep, with uniform thermal properties and a surface temperature that varies sinusoidally, the boundary conditions of z = 0 and z→∞ were applied, and it was also assumed that at infinite depth (z→∞), the temperature is equal to constant, T a. Thus, the temperature at the surface and infinite depths would be expressed respectively as Eqs. (7) and (8)

$$ T\left(0,t\right)={T}_{\mathrm{a}}+{A}_0\sin wt $$
(7)
$$ T\left(\infty, t\right)={T}_{\mathrm{a}} $$
(8)

Applying these boundary conditions to Eq. (6) yields

$$ T\left(z,t\right)={T}_{\mathrm{a}}+{A}_0{e}^{-\raisebox{1ex}{$z$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}\sin \left( wt\kern0.5em -\kern0.5em \begin{array}{c}z\\ {}\overline{\mathrm{d}}\end{array}\right) $$
(9)

where T (z, t) is the ground temperature at time (t, day number of year) and ground depth (z), T a is the average ground temperature (°C), A 0 is the annual amplitude of the surface ground temperature (°C), and d is the damping depth of daily variation.

The damping depth is defined as

$$ \mathrm{d}={\left(2\alpha /\omega \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} $$
(10)

where ω = 2π/365 day−1 is the radial frequency, and for annual variation, the period is 365 days.

It could be seen from Eq. (10) that the annual variation of surface temperature which has low-frequency oscillation will penetrate the ground than diurnal wave which is of higher frequency. From Eq. (9), the amplitude of soil temperature waves is

$$ A\left(\omega, z\right)={A}_0\left(\omega \right){e}^{-\raisebox{1ex}{$z$}\!\left/ \!\raisebox{-1ex}{$d$}\right.} $$
(11)

while the expression for phase is

$$ \theta \left(\omega, z\right)=\raisebox{1ex}{$z$}\!\left/ \!\raisebox{-1ex}{$d$}\right. $$
(12)

Plotting the graph of the natural logarithm of amplitude against depth and graph of phase angle in radian against depth will produce straight lines if the ground is homogeneous. The slope of amplitude graph and phase angle graph are \( -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d$}\right. \) and \( \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d$}\right. \), respectively. The closeness, or otherwise, of the values of d obtained from the two methods confirms, or otherwise, the homogeneity of the ground at the site (Gilman 1977).

Equation (9) could be re-written as

$$ T\left(t,z\right)={T}_{\mathrm{a}}+{A}_0{e}^{\raisebox{1ex}{$-2\pi z$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\sin 2\pi \left(\frac{t}{p}-\frac{\gamma }{p}-\frac{z}{\lambda}\right) $$
(13)

where λ is the wavelength, γ is the phase displacement in days at the surface, and p is the period (which is equal to 365 days). From Eq. (13), the phase is \( 2\pi \left(\frac{\gamma }{p}-\frac{\gamma }{p}\right) \) and the amplitude is given as \( {A}_0{e}^{\raisebox{1ex}{$-2\pi z$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.} \), that is

$$ \theta \left(\omega, z\right)=2\pi \left(\frac{\gamma }{p}-\frac{z}{\lambda}\right)\kern0.24em \mathrm{and} $$
(14)
$$ A\left(\omega, z\right)={A}_0{e}^{\raisebox{1ex}{$-2\pi z$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.} $$
(15)

Comparing Eqs. (14) and (15) with equations of straight lines obtained from the graph of natural logarithm of amplitude and phase against depth yields values of γ, λ, and d, which can be used to estimate thermal diffusivity.

Results and discussion

Field measurements: variation of ground temperature with depths

Annual meteorological data of Abeokuta during 2014, obtained from the Department of Agrometeorological and Water Management of Federal University of Agriculture Abeokuta and Nigeria Meteorological Agency, gave a minimum air temperature of 17.72 °C in August and a maximum air temperature of 36.9 °C in February. The relative humidity varied from 39.5% in January to 96.7% in July. Wind speed varied from 0.58 km/h (0.36 miles/h) in December to 19.15 km/h in February. The rainfall was at its peak in July (322.9 mm) and least in December (0.00 mm). Evaporation was least in August (1.5 mm) and highest in April (5.7 mm). The monthly average hours of sunshine varied from 75 h (minimum) in August to 205 h (maximum) in December.

The variation of ground temperature with respect to depths was studied by plotting graphs of depths against soil temperature (Fig. 3). This gives the profile of ground temperature based on 1-year monthly averages. The amplitude of temperature (Fig. 3) was 32.6 °C at a depth of 2 cm and decreased to 26.2 °C at a depth of 200 cm. The decline in amplitude was exponential. The trend of the ground temperature with respect to depth was seasonally varied. During the dry season (November to April), temperature decreased from the surface to deeper depth while it increased with depth during the rainy season (May to October). The capacity of the ground to transfer heat increases as the amount of water in the ground increases (Alnefaie and Abu-Hamdeh 2013).

Fig. 3
figure 3

Relationship between monthly average ground temperature and depth

Full size image

The ability of soil to transfer heat increases because water conducts heat 25 times more than air; therefore, as water content increases, separated soil particles become connected by this water (Max 1949; Balaji et al. 2014). Since contact is needed for the effectiveness of heat transfer by conduction, increased contact increases the flow of heat in the ground. Substantial heat is also required to raise the temperature of water; therefore, as the water content of the ground increased, the heat capacity of the soil increased and it takes longer time for the ground to warm up. Clay soil is often colder than neighboring sandy or loamy soil in the dry season because of its ability to hold more water than the duo. Clay soil requires more heat to raise its temperature. A decrease in ground water content reduces the heat capacity of the ground and allows for a more rapid increase in ground temperature. Heat travels rapidly from the surface during the dry season than during the rainy season because part of the heat that was traveling would have been expended in warming up the water. Smith (1929) and Michal (2014) reported that range in both diurnal and annual ground temperatures is influenced largely by weather condition like rainfall, sunshine, or ground moisture as well as the direction and intensity of the wind, all these, in turn, vary with season.

It was observed that the ground temperature declined during the dry season but increased during the rainy season. This could have resulted from better heat transfer by conduction which has been reported to increase with ground moisture (Alvala et al. 2002). Since the ground water content during the dry season was low allowing for more air in the pore spaces, the rate of heat transfer within the ground profile would reduce since air is a poor heat conductor than water (Max 1949; Balaji et al. 2014).

The clay content of the ground which increased with increasing ground depth could also have affected the volumetric water content of the soil, thereby causing an increase in heat transfer. The sandy surface layer, on the other hand, is highly porous, having more air spaces and lower gravimetric water content, and since the pore spaces are predominately occupied by air, heat transfer will be slower than in the subsurface depths where the soil particle is predominated by clay (Nwankwo and Ogagarue 2012).

In the graph of ground temperature against depth (Fig. 4), ground temperature varied from 27.75 °C at depth 200 cm to 29.9 °C at 2 cm. The difference gave the soil temperature range from the surface to the depth 200 cm within the study area during the year.

Fig. 4
figure 4

Depth against annual average ground temperature

Full size image

For soil classification, the soil temperature is usually measured at 50 cm depth. This is based on the assumption that soil temperature below 50 cm remains fairly constant. However, this study revealed that the soil of Abeokuta has temperature that fluctuated (decreasing with depth) between 0 and 50 cm depth and between 150 and 200 cm depth (Table 1). However, the temperature of the ground was fairly constant between 50 and 150 cm. Thus, the soil temperature regime of Abeokuta soils can be estimated better within this depth range (50 and 150 cm).

Table 1 Annual mean soil temperature and annual mean amplitude
Full size table

The annual mean soil temperature and annual mean amplitude for each depth were calculated (Table 1). The decrease in temperature experienced is due to the effect of the ground that acts as a heat sink, which absorbs heat energy as the wave traveled through the ground. The heat waves lost part of its energy and amplitude to the ground as it decreased from 4.10 °C at 2 cm to 0.06 °C at 200 cm. The temperature also decreased from 30.09 °C at 2 cm to 27.73 °C at 200 cm. The standard deviation calculated for ground temperature and amplitude at each depth also showed the same trend as they decreased with increasing depth through the ground except the mean amplitude of heat waves at 200 cm which was out of trend.

Evaluation of Fourier harmonic of soil temperatures

The monthly average ground temperatures at various depths are presented in Table 2.

Table 2 Monthly average ground temperature at various depths
Full size table

The monthly period was adopted because it was sufficient to ensure accuracy in fitting the harmonics. Though hourly or daily data too will give accurate harmonic analysis, it may be too cumbersome to handle. The monthly average ground temperatures at depths 2, 50, 100, 150, and 200 cm were subjected to Fourier analysis using Eq. (1). Three harmonics were calculated for each of the five depths below the surface. Lemmela (1970) reported that two harmonics are sufficient to describe the observed ground temperature while other higher harmonics contribute insignificantly to the improvement of the Fourier analysis. The observed monthly average temperature and calculated temperatures from the Fourier equation of first, first two, and first three harmonics for each depth are shown in Tables 3 and 4), though the harmonic analysis was performed on all depths (2, 50, 100, 150, and 200 cm); for brevity, only results from two depths (2 and 50 cm), which fall within the ground surface, were displayed.

Table 3 Harmonic analysis of ground temperature at 2 cm for first, second, and third harmonics
Full size table
Table 4 Harmonic analysis of ground temperature at 50 cm for first, second, and third harmonics
Full size table

The plots of observed monthly ground temperature and calculated ground temperature for first, second, and third harmonics at 2 and 50 cm (Figs. 5 and 6) were sinusoidal, having maximum and minimum temperatures in February/March and August, which fall within the dry and rainy seasons, respectively. As predicted by West (1952) and Lemmela (1970), the first two harmonics described better the annual ground temperature variation at all depths except at depth 150 cm.

Fig. 5
figure 5

Observed and calculated ground temperatures at 2 cm

Full size image
Fig. 6
figure 6

Observed and calculated ground temperatures at 50 cm

Full size image

Determination of thermal diffusivity of the soil

The equations of the best line for phase and amplitude in Fig. 7 are respectively 16 and 17.

Fig. 7
figure 7

Ln (amplitude) and phase against depth

Full size image
$$ \theta =0.0046z-0.5402 $$
(16)
$$ {\mathrm{Log}}_eA\left(\omega, z\right)=0.0044z+0.9853 $$
(17)

Comparing Eqs. (14) to (17), we obtained γ = 31.38 and λ = 13.74 m from the phase angle while the value of λ obtained from amplitude angle equation was 14.3 m and A 0 = 2.68 cm. The estimate of λ from both methods was in good agreement. The gradients of phase and amplitude graphs (Fig. 6) are − 0.0044 and 0.0046, respectively; these are equivalent to the inverse of damping depths \( -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d$}\right. \) and \( \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d$}\right. \) (Eqs. (11) and (12)). The values of damping depths obtained from two graphs were very close, which suggests the homogeneity of the soil at the study area.

Applying Eq. (10), the thermal diffusivity from phase lag was \( \alpha =\frac{d^2\pi }{p}=5.1463\times {10}^{-7} \) m2/s while the thermal diffusivity from amplitude ratio was α = 4.708 × 10−7 m2/s. Thermal diffusivity was also calculated from the change of phase as a function of depth and from the change of amplitude as a function of depth (Table 5).

Table 5 Diffusivity based on the results of Fourier analysis
Full size table

The correlation coefficient between observed and calculated monthly ground temperatures at different depths for harmonics 1, 2, and 3 (Table 6) increased with depth in the soil except at depths 50 and 200 cm. Further calculations of second and third harmonics did not contribute appreciable improvement.

Table 6 Correlation coefficient between the observed and simulated monthly temperatures at different depths
Full size table

Variance explained by different harmonics

Variance is the sum of contribution of individual coefficient of harmonic and is given by

$$ {\sigma}^2=\frac{1}{2}\sum_{n=1}^{\infty}\left({a}_{n_n}^2+{b}_n^2\right)=\frac{1}{2}\sum_{n=1}^{\infty }{A}_n^2\kern0.35em \mathrm{where}\kern0.2em {A}_n^2={a}_n^2+{b}_n^2 $$
(18)

The contribution of different harmonics to the total variance expressed in percentages is presented in Table 7. Contributions of variance from harmonics increased with depth, and contributions from second and third harmonics were not that significant. The mean value for all depths was also calculated.

Table 7 Contribution of each Fourier harmonic to the simulated waves
Full size table

Conclusion

The study presented field experimental results of measured ground temperature at five depths. Fourier analysis for three harmonics was developed, of which the first harmonic described the ground temperature variation to 95.07% while the first two harmonics described the variation to 98.72%. Further harmonics contribute insignificantly to the improvement of the variation. The annual damping depth of the study area calculated from the slope of phase graph and the slope of amplitude graph and directly from the daily average ground temperature were 217.39, 227.27, and 217.90 cm, respectively.

Ground thermal diffusivity obtained from the slopes of phase and amplitude graphs demonstrated agreement with the value obtained from daily average temperature. The study revealed that the annual ground temperature varied from 27.75 °C at depth 200 cm to 29.9 °C at 2 cm. The diurnal temperature range for depths between 2 and 200 cm during the dry season was higher (about 18 °C) than that during the rainy season (about 12 °C). The study revealed that the ground temperature decreased between depths 0 and 50 cm and between 150 and 200 cm but remained fairly constant between 50 and 150 cm.