Introduction

Rainfall is as a key factor in hydrological regime (Valipour 2016; Sangati and Borga 2009). It is the result of a thermal and atmospheric change (Hamlaoui-Moulai et al. 2013), as it constitutes the main input in watershed systems (Palecki et al. 2005). Rainfall as a random variable is a constraint that may limit the policy actions both on the macro-economic and micro-economic scales, especially for countries suffering from lack of water resources (Valipour 2015a, Valipour 2015b; Valipour et al. 2015). Indeed, this variable may cause a significant risk when it comes to establish strategies without considering it (Valipour 2015c, 2012; Touchan et al. 2011; Delli et al. 2002) especially in areas with frequent droughts. Rainfall variable fluctuate in space and time. Its amount and distribution are affected by many factors including geographical, such as longitude, latitude, altitude; distance from sea; seasonality, like air humidity movement, temperature, atmospheric pressure (Slimani et al. 2007) and topography (Subyani 2004; Zekai and Zeyad 2000; Chua and Bras 1982; Rosenberg 1969). Many studies have been conducted to correlate rainfall with the above-mentioned factors based on mathematical modelling (multiple regression, interpolations, etc.) as an alternative to improve rainfall estimation using data provided from available rain gauges (Marks et al. 2013; Lloyd 2005; Naoum and Tsanis 2004; Brunsdon et al. 2001; Goovaerts 2000; Johnson and Hanson 1995; Hevesi et al. 1992). Multiple linear regression (MLR) is a well-known method of mathematics modelling the direct linear relationship between a dependent variable and one or more independent variables (Sheather 2009; Walpole et al. 2007). It has been widely used for the estimation of climate variables (Cook et al. 1994). Independent variables generally include station location and elevation in areas where climate is significantly correlated to topography (Hay et al. 1998; Goodale et al. 1998) and have been applied with a number of topographic variables in order to analyse orographic rainfall. Precipitation could be incorrectly estimated if topographic variables influencing precipitations are not considered (Myoung-Jin et al. 2012). However, maximum cumulative rainfall does not necessarily coincide with the highest altitude (Subyani and Al-Dakheel 2009). Lloyd 2010; Ahrens 2006; and Prise et al. 2000, reported that rainfall can be estimated in space through an interpolation method with simple mathematical models (inverse distance weighting, analysis of surface trend, fluting and Thiessen polygons, etc.). Moreover, rainfall can be estimated through a more complex method relying on kriging (Skirvin et al. 2003). Actually, geostatistical interpolation has become an important tool in climatology as it takes into consideration spatial variability and quantifies the estimation uncertainty. Ashiq et al. 2010; Skirvin et al. 2003; Goovaerts 2000; and Matheron 1965, reported that geostatistical interpolation methods are based upon the structure of a variable’s spatial continuity (variable with a random regionalized character). Only the spatial relationship between the sampling points is considered; the other topographical variations are not taken into account. Geostatistical approach provides a set of statistical methods that describe a spatial autocorrelation of the sample data or a natural phenomenon (Slimani et al. 2007; Kyriakidis and Journel 1999; Lam 1983). It is also used for spatialization and mapping of estimated data points from the values of targeted variable in non-sampled locations (Piccini et al. 2012). Variogram is the structure function used to model the variability of a phenomenon. It measures the variability between pairs of variables and it is expressed as a function of distance between points (Delhomme 1976). GIS can serve geostatistics to help with georegistration of data, for easier spatial explanation.

Actually, one of the main preoccupations of researchers is to provide decision-makers with tools to better adapt the future strategies of sustainable development and natural resource management. The importance of precipitation analysis in different parts of Algeria has been addressed previous studies. However, rainfall representations were developed without considering rainfall trend, region’s climate or other factors influencing this random variable in except few recent studies in which rainfall characterization was developed using new methods (Meddi and Toumi 2015: Ouallouche and Ameur 2014: Benabdesselam and Amarchi 2013: Smadhi and Zella 2012). The novelty of the current work is that its output has a direct and important impact on sustainable development of cereal cultivations in the region on one hand. On the other hand, to the best of the authors’ knowledge, it is the first study that combines two approaches in order to better estimate precipitation at the spatio-temporal plan and to determine the rainfall gradient structure in the study area. The first approach based on multiple linear regression between rainfall and geographical feature (altitude, latitude and longitude) to get the weighting of each parameter and the second approach based on geostatistical calculation including explanatory information to represent the spatial and temporal distribution of average annual rainfall in the eastern high plateaus region of Algeria. This combined method was set in order to optimize rainfall representation based on data treatment given by conventional measures provided by a poor rain-gauging network. The spatial and temporal distribution of rainfall in the study area was elaborated through digital mapping where isohyet shape clarifies the rainfall behaviour in the region. The choice of this area is justified by its strategic and economic importance for sustainable development. It is historically considered as a potential producing area of cereals. Therefore, it is worthwhile to study the hydro-climatic distribution on this area in order to optimize stakeholder’s interventions and the arising results are of crucial importance for agricultural development and environmental issues.

Study area description

Algeria is located in North Africa, with a total area of 2,381,741 km2; it is bounded on the north by the south shore of the Mediterranean Sea and to the south by the Sahel region. It is situated in the transition zone between the Mediterranean sub-humid and humid climate in the north, and arid Saharan climate in the south (Queney Queney 1937, 1943 ). The northern part is characterized by a cold-rainy winter and a hot-dry summer. Moreover, the climate of Algeria presents a clear east-west and north-south apparent hydro-climatic gradients. The latter, integrator of strong spatial and temporal variability, is more important as many factors are involved for its enhancement (Seltzer 1948). The distribution of precipitation is very heterogeneous and varies generally according to the relief and the distance from the sea (Touazi et al. 2004). In addition, the yearly rains in the north part of Algeria were distributed according to a normal root distribution (Chaumont and Paquin 1971). However, northeast of Algeria is subjected to very irregular spatio-temporal variations (Meddi and Toumi 2013).

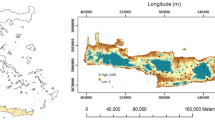
The study area is located in the eastern high plateau region of Algeria, known for its predominantly semi-arid bioclimatic affiliation. It stands between 4.2° to 8.3° latitude north and 35.00° to 36.6° longitude east, extending over an area of 33,610 km2 with a perimeter of 1872 km (Fig. 1).

Fig. 1
figure 1

Rain-gauging stations displayed over digital elevation model (DEM) of the study area

Full size image

Several chains of mountains naturally limit the study area. To the north, the Atlas chain is including the mountains of Constantine and Sidi-Dris with the highest points reaching 1285 and 1363 m, respectively. In the northwest is the Djurdjura Mount with a culminating point reaching 2308 m (Lala Khedidja crest). To the west is the Bibans with the relatively high points (Takoucht Mont, 1900 m, and Megress Mont, 1737 m), the highest point reaching 2000 m at Babor Mont. To the east are the mountains of Tébessa (Doukhane and Bou-Roumane Monts) with the highest points reaching 2249 and 2250 m, respectively. To the south, the Saharan Atlas chain includes the Aurès Mountains, Mahmal and Zellatou Mounts with culminating points approaching 1550 m. Moreover, the study area is dominated by plains with very low slopes (0–5 %). The main plains are those of Bordj Bou Arreridj, Setif, Oued El Othmania and El Khroub at Constantine. Furthermore, other plains occupy the area, plains of Mila in the north and plains of Touffana and Batna in the south (Bahlouli et al. 2008).

Methods and materials

Rainfall data base

The prospective work is necessary to identify data sources and to select reliable and relevant data to the objective of our study. The data processing of annual rainfall series, covering a period of 22 years (1986–2007), were collected from professional and auxiliary meteorological stations belonging to the National Meteorological Office (NMO) and from rainfall stations belonging to the National Agency for Water Resources (NAWR). All measured precipitations were in liquid form and the supplier institutions homogenized the rainfall data series. A survey was conducted to identify 95 rain-gauging stations across the study area, but it was found that some stations contained incomplete data and were operating in heterogeneous periods. Therefore, 65 rain-gauging stations were selected, for their complete dataset. For a practical presentation of graphics and an ease of interpretation, a code number was attributed to each rain-gauging station (Table 1).

Table 1 Geographical coordinate of rain-gauging stations
Full size table

MLR and cross validation tests

In order to estimate the local gradient of dependent variable “rainfall”, Statistica 6.0 software was used to perform a MLR analysis with latitude, longitude and altitude as independent variables. Regression analysis is given by the model equation defined in Eq. (1):

$$ P={\beta}_1X+{\beta}_2Y+{\beta}_3Z+{\beta}_0+\varepsilon $$
(1)

where P represents rainfall as dependent variable. β 1, β 2 and β 3 are the multiple regression coefficients of the respective independent variables X, Y and Z, where X represents latitude, Y longitude and Z altitude. β 0 represents the intercept and ε the errors. Once the regression model has been constructed, a cross-validation technique was applied to confirm the goodness of fit of the statistical model, including the analysis of multiple R, R 2, R 2-adjusted analysis (Cook 1977) and the statistical tests F test, t test, root mean squared error (RMSE) and standardized mean squared error (SMSE) (Bostana et al. 2012; Walpole et al. 2007; Vargas-Guzman et al. 2000; Dingman et al. 1988; Snee 1986).

The multiple R is the positive square root of R 2 (the coefficient of multiple determinations). R 2 is a measure of the proportion of variability explained by the fitted model. It is calculated as follows:

$$ {\displaystyle {R}^2}=\frac{SSR}{SST}=1-\frac{SSE}{SST} $$
(2)

where:

$$ \left.\begin{array}{cc}\hfill SSE={\displaystyle \sum_{i=1}^n{\varepsilon}_i^2}\hfill & \hfill \mathrm{Sum}\kern0.5em \mathrm{of}\kern0.5em \mathrm{squares}\kern0.5em \mathrm{error}\hfill \\ {}\hfill SST={\displaystyle \sum_{i=1}^n{\left({P}_i-\overline{P}\right)}^2}\hfill & \hfill \mathrm{Total}\ \mathrm{sum}\ \mathrm{of}\ \mathrm{squares}\hfill \\ {}\hfill SSR={\displaystyle \sum_{i=1}^n{\left(\underset{\mathrm{i}}{\widehat{P}}-\overline{P}\right)}^2}\hfill & \hfill \mathrm{Regression}\ \mathrm{sum}\ \mathrm{of}\ \mathrm{squares}\hfill \end{array}\right\} $$
(3)

where n is sample size (number of observations), P i observed value of rainfall and \( \underset{\mathrm{i}}{\overset{\hat{\mkern6mu} }{P}} \) predicted rainfall value.

R 2adj is estimated by dividing SSE and SST by their respective degrees of freedom as follows:

$$ {\displaystyle {R}_{adj}^2}=1-\frac{SSE/\left(n-k-1\right)}{SST/\left(n-1\right)} $$
(4)

where n is the number of observations, k is the number of variables, and (n − k − 1) and (n − 1) represent the degrees of freedom of SSE and SST, respectively.

F-test (Fisher) is a statistical test in which the test statistic has an F-distribution under the null hypothesis. It is calculated as follows:

$$ F=\frac{SSR/k}{SSE/\left(n-k-1\right)} $$
(5)

where k and (n − k − 1) are respective degrees of freedom of SSR and SSE.

The t test most often used in multiple regression tests the significance of individual coefficients. It is calculated as follows:

$$ t=\frac{\beta_j-{\beta}_{j0}}{s\sqrt{\sigma }} $$
(6)

with s 2 = SSE/(n − k − 1) and Β j coefficient (j = 0,1,2,…k).

These tests often contribute to what is termed variable screening, where the analyst attempts to reach the most useful model (Walpole et al. 2007).

The appropriateness of the chosen model is tested using the cross-validation technique based on standardized mean squared error (SMSE) and root mean squared error (RMSE) which are used together to diagnose the error variation in a set of forecasts (Bostana et al. 2012; Lloyd 2005; Miniscloux et al. 2001; Vargas-Guzman et al. 2000; Dingman et al. 1988). The RMSE is used as a measure of error’s magnitude. It is calculated as follow:

$$ \mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum_{i=1}^n{\left\{z\left({x}_i\right)-\overline{z}\left({x}_i\right)\right\}}^2}} $$
(7)

SMSE is the average ratio of the squared prediction error at validation points and the corresponding prediction error variance.

$$ \mathrm{SMSE}=\frac{1}{n}{\displaystyle \sum_{i=1}^n\frac{{\left\{z\left({x}_i\right)-\overline{z}\left({x}_i\right)\right\}}^2}{\sigma_{PE}^2\left({x}_i\right)}} $$
(8)

with \( {\sigma}_{PE}^2\left({x}_i\right) \) as the prediction error variance at location x i .

Spatial pattern analysis and geostatistical approach

A digital elevation model (DEM) with a cell size of 30 m (Fig. 1) was generated from the highest elevation point values and equidistance digital maps provided by the Algerian National Institute of Maps and Remote Sensing (NIMRS). DEMs were developed using “vertical mapper 3.0” extension of mapinfo 7.5 software. The influence of geographic parameters affecting rainfall was identified through multiple linear regression analysis. Geostatistical calculation for variogram adjustment was performed using “VarioWIN 2.2” software (Pannatier 1996) and inter-yearly rainfall mapping was achieved using “Surfer 8.0” and “Mapinfo 7.5” software.

Geostatistical interpolation method of rainfall is based on the spatial continuity structure of this variable. It provides a set of statistical methods that describe a spatial autocorrelation of the sample data of rainfall. In its overall conception, the kriged or predicted value Z(x 0) is a linear combination of observations at N nb neighbour stations (Bargaoui and Chebbi 2009). Kriging is applied to estimate the values of the rainfall unsampled locations using the points around it. The kriging estimation is expressed as follows:

$$ Z\left({x}_0\right)={\displaystyle \sum_{i=1}^{N_{nb}}\kern1em {\lambda}_iZ\left({x}_i\right)} $$
(9)

with Z(x 0) as the estimator of the mean Z on x 0 and Z (x i ) the known value Z at the point x i . N nb are a number of data points used for estimation and λ i are kriging weights which are estimated as a solution of the kriging system. The weightings involved in the linear combination are obtained by solving the minimization problem whose equations depend on the theoretical variogram and the geometric configuration of rainfall data point’s knowledge (Arnaud and Emery 2000). The equation of semi-variogram is expressed as follows:

$$ \gamma (h)=\frac{1}{2m}{\displaystyle \sum_i^m\kern1em {\left\{Z(Xi)-Z\left( Xi+h\right)\right\}}^2} $$
(10)

where h is the distance between X i and X j , and m is the number of pairs which are separated by the distance h. The obtained variogram is characterized by the nugget effect, the range and the Sill. The experimental variogram is adjusted on theoretical models based on the value of the Indicative Goodness of Fit (IGF) which is a basic criterion for the selection of the adjusted variogram model (Pannatier 1996). An IGF value close to zero indicates a good fit of the model.

Results and discussion

Considering the standards for meteorological station setting, whose approximate coverage tends from 20 to 40 km2 in plains and 2 to 10 km2 in mountainous area (Bertrand-Krajewski et al. 2000), the density of rain-gauging stations in the study area is low. Fundamental statistics tests for yearly rainfall data were applied to characterize the location and variability of a data set. As can be seen in Fig. 2, the average annual rainfall values are fluctuating considerably from one gauge station to another varying between an interval of 127 mm in Ain Kercha (code 32) and 752.2 mm in Beni Aziz (code 52). The average annual rainfall of the study area is 362.5 mm with a coefficient of variation of 0.33 and a standard deviation of 122.33 mm (Table 2).

Fig. 2
figure 2

Yearly rainfall recorded in rain-gauging stations across the study area for the period of 1986 to 2007

Full size image
Table 2 Descriptive statistics and normality test of used data
Full size table

A further skewness, Kolmogorov-Smirnov and kurtosis tests were applied to characterize rainfall frequency and its distribution shape. The computed Kolmogorov-Smirnov test value (K-S = 0.1) at null hypothesis was less than the corresponding critical value of significance (p = 0.614). Thus, the hypothesis regarding the distributional shape is not rejected as the K-S value is smaller than the critical value of significance. Moreover, in Table 2, the skew value is equal to 0.85, indicating that the distribution is moderately skewed with an asymmetric tail extending toward positive values. The calculated kurtosis value (1.52) is lower than 3, while a normal distribution has a kurtosis of 3 (Bulmer 1979), indicating that the distribution is Platykurtic, which means that the probability for extreme values is less than a normal distribution and the values are wider spread around the mean (Walpole et al. 2007; Bulmer 1979).

A rain-specific MLR model is developed for all 65 rain-gauging stations, using cumulated yearly rainfall variables of each station. From the interactive model regression analysis, the coefficient values found were as follows: β 1 = 261.25, β 2 = 17.06, β 3 = 0.04 and the intercept β 0 = −9159. By inputting the obtained results in Eq. (1), the equation of annual rainfall obtained from regression analysis becomes

$$ P\left(\mathrm{mm}\right)=261.25X+17.06Y+0.04Z-9159+\varepsilon $$
(11)

with X, Y and Z being, respectively, latitude, longitude and altitude. ε represents error of estimation and it is equal to 89.92. Table 3 displays the regression coefficients values and the validation tests of the MLR model. According to Table 3, the goodness of fit of rainfall MLR model has relatively low multiple R, R 2 and adjusted R 2 (R 2 = 0.595, multiple R = 0.703 and the adjusted R 2 = 0.515). F-test was used to check the overall significance of the developed MLR model. The advantage of the F-test over R 2 is that the F-test takes into account the degrees of freedom, which depend on the sample size and the number of predictors in the model (F (3.61) = 19.41, p value = 0.00000). In addition, t test, RMSE and MSE were used to evaluate the performance of the MLR equation (t = −7.126, p level = 0.00000, RMSE = 0.15, MSE = 0.023) indicating that indeed the MLR model is significant at the 0.05 confidence level. Moreover, X (t = 7.454, p = 0.000000) and intercept β 0 (t = −7.454, p = 0.000000) are highly significantly explanatory variables, indicating higher t values and very low p value at the 95 % significance level. However, Y (t = 1.354, p = 0.180) and Z (t = 0.758, p = 0.450) are statistically insignificant in the MLR estimation.

Table 3 Coefficients of the MLR application and validation test
Full size table

Equation (11) shows the impact of each geographic parameter on rainfall. The weight of latitude, with a coefficient of 261.25, is the most important among the weights of the other parameters. With a coefficient of 17.06, longitude affects slightly rainfall. Moreover, altitude with a coefficient of 0.04 has insignificant effect on precipitation. This may be due to the fact that the relief is not sufficiently contrasted in the study area. To better explain this situation, a slope map of the region was developed (Fig. 3).

Fig. 3
figure 3

Slope range distribution in the study area

Full size image

Around 29,738 km2 consists mainly of height plateaus with low slopes (<5 %), representing 88.5 % of the total study area and 11 % covers areas with a slope ranged between 5 to 10 % (Table 4).

Table 4 Slope range distribution of the study area
Full size table

The majority of rain-gauging stations (45 stations, see Table 1) are located between 800 and 1100 m elevations. To check whether precipitation is correlated to altitude, the correlation coefficient was calculated according to Eq. 12 expressed as follows:

$$ P=324.93+0.056\ Z $$
(12)

where R = 0.099, P: rainfall (mm), and Z: altitude (m).

The calculated R confirm the insignificant correlation (R = 0.099) between rainfall and altitude (Fig. 4).

Fig. 4
figure 4

Correlation between rainfall and altitude

Full size image

According to the MLR model, 59.5 % of the observed variability of rainfall is attributed to the geographical parameters (R 2 = 0.595), leaving 40.5 % residual variance attributable to unmeasured complications. Multiple regression in this case gives a more accurate description of the regional distribution of precipitation; it appears that the intercept (−9159) plays an important negative impact on the annual rainfall. This result indicates that the rainfall is influenced by other environmental factors such as distance from sea, air humidity movement, land cover vegetation, temperature and atmospheric pressure (Subyani 2004; Zekai and Zeyad 2000; Chua and Bras 1982; Rosenberg 1969). Rainfall spatial variability is clearly related to a north/south gradient. Considering the position of the study area, which is situated on the southside of the Tellian Atlas chain, the northern part of this area can take much advantage of orographic rains contrarily to the central and south part (Miniscloux et al. 2001). High temperatures and dry air masses coming from the Sahara generate warm front that is playing the role of barrier against the cold front coming from the north. In addition, the lack of vegetation in the study area, which is dominated by annual crops like wheat and barley, contributes to reduce rainfall amounts.

The achievement of directional variograms from rainfall data, according to the north/south and east/west directions, permitted to identify the structure of the rainfall phenomenon. Results revealed that directional variograms fit well with the theoretical power and Gaussian variograms respectively in both this two directions. Table 5 lists the variogram parameters and the cross-variogram test.

Table 5 Theoretical variogram parameters
Full size table

Figures 5 and 6 illustrate the structure of variograms which fit a power model with a best fit found value equal to 1.44e−3 and a Gaussian model with best fit found (IGF) equal to 4.98e−2, respectively. The linear structure of the power variogram indicates the existence of a drift. Thus, rainfall varies faster toward the north/south direction. In addition, variograms show the existence of increasing range of fluctuations limited to the distances of 171 and 100 km, respectively (Table 5). The nugget effect denotes the existence of rapid fluctuations undetectable by the climate network set in place. The Gaussian variogram with higher nugget effect indicates the existence of a microclimate in the region (Slimani et al. 2007).

Fig. 5
figure 5

Adjusted theoretical variogram of mean yearly rainfall according to the north/south direction

Full size image
Fig. 6
figure 6

Adjusted theoretical variogram of mean yearly rainfall according to the east/west direction

Full size image

Ordinary kriging interpolation was applied for the precipitation data in order to perform isohyet mapping. Figure 7 shows the vertical rainfall distribution and the north/south contrast effect in the study area. The isohyets are generally arranged in parallel to the northern orographic barriers. The horizontal organization of mount chains delimiting the northern part of the study area lead to upstream interception of clime disturbances coming from the north. Thus, the rain bands greater than 500 mm occupy the northern part of the area representing 12.41 % where 10 % of the total study area is affected by the rain band ranging from 500 to 550 mm. In the central part of the study area, isohyets follow a clear north/south gradient caused by hot and dry air masses coming from the south emphasized during the months of sirocco. The rain bands covering isohyets 300 to 400 mm dominate 58 % of the study area, followed by the rain band 400 to 500 mm (24.31 %). In the far east region of the study area, the rain bands adopt an east/west gradient; this could be due to humid airflow masses coming from the Mediterranean Sea through Tunisia, thus promoting rainfall to the limits of Tunisian border. Also, circular rain pockets that appear in the central part of the region substantiate the presence of a microclimate as demonstrated by the higher value of nugget effect detected (Table 5).

Fig. 7
figure 7

Spatio-temporal map of rainfall distribution (mm) for the period 1986–2007 in the eastern high plateau region of Algeria

Full size image

Rainfall bands ranging from 200 to 350 mm cover 39.25 % of the area should be dedicated exclusively to the cultivation of barley with supplemental irrigation for areas with annual rainfall amount less than 300 mm. Rain bands ranging from 350 to 500 mm occupy 48.32 % of the study area is suitable for the cultivation of durum wheat with supplemental irrigation for areas with annual rainfall amount less than 450 mm. Rain bands greater than 500 mm is more favourable for the cultivation of bread wheat (Triticum aestivum).

Conclusion

The present hydro-meteorological study estimates the precipitation potential of Algeria’s eastern high plateau region. The results show the importance of considering the influence of geographical parameters on the spatial rainfall distribution.

Rainfall data provided from rain-gauging station may be inadequate to define and delimit vulnerable areas, and traditional mapping is of little help when the uncertainty associated with the estimated values at unsampled locations is required to support decision-making. In this study, MLR associated to geostatistical methods give a useful tool to generate rainfall map and to assess the uncertainty of the predicted values as an alternative to a detailed investigation. The geostatistical analysis indicates the existence of a drift, supporting the MLR results concerning the existence of a strong north/south rainfall gradient in the study area. The large extent of the study area and its economic importance underline the importance of strengthening and expanding the current climate network. The complexity of rainfall estimation in the region suggests the requirements to consider other variables, such as temperature, air masses movement and land cover vegetation, to better understand the influence of these parameters on rainfall. Rain bands greater than 350 mm are considered as potentially suitable for cereal crops, occupying about 61 % of the total study area.

Moreover, applying this method will not only provide better rainfall estimation but could be used efficiently for monitoring and development of such areas that are particularly intended for agronomic activities, potentially advocated to the production of winter wheat and barley. The stakeholders must respect this repartition in order to optimize crop yields. Finally, the proposed approach provides a useful tool that could be easily applied to other regions with poor rain-gauging network; it could also be used for other climatic parameters needed for climatology investigation and environmental and agronomic studies.