A claims problem approach to the cost allocation of a minimum cost spanning tree

Abstract

We propose to allocate the cost of a minimum cost spanning tree by defining a claims problem and using claims rules, then providing easy and intuitive ways to distribute this cost. Depending on the starting point that we consider, we define two models. On the one hand, the benefit-sharing model considers individuals’ costs to the source as the starting point, and then the benefit of building the efficient tree is shared by the agents. On the other hand, the costs-sharing model starts from the individuals’ minimum connection costs (the cheapest connection they can use), and the additional cost, if any, is then allocated. As we prove, both approaches provide the same family of allocations for every minimum cost spanning tree problem. These models can be understood as a central planner who decides the best way to connect the agents (the efficient tree) and also establishes the amount each agent has to pay. In so doing, the central planner takes into account the maximum and minimum amount they should pay and some equity criteria given by a particular (claims) rule. We analyze some properties of this family of cost allocations, specially focusing in coalitional stability (core selection), a central concern in the literature on cost allocation.

1 Introduction

Consider a group of individuals who want to be connected to a water supply, or a telephone or cable TV network. These individuals are located at different places, and they have some (different) fixed costs of linking with any other individual or linking to the source. The purpose of the group is to be connected to the source at the cheapest possible way (the minimum cost spanning tree). The allocation of this cost among the individuals in the network, once the optimal spanning tree is obtained, is an issue deeply studied in the literature, where different solutions have been proposed: Bird rule (Bird 1976), Kar (Kar 2002), Folk (Feltkamp et al. 1994; Bergantiños and Vidal-Puga 2007), Cycle-complete (Trudeau 2012), or the Serial cost sharing rule (Moulin and Shenker 1992).

The present paper aims to define new methods of sharing the cost of the optimal network by associating a claims problem to each minimum cost spanning tree situation and then using claims rules to allocate the total cost.

Claims problems are characterized by an endowment (to be distributed among the agents) and a claim from each agent (the maximum amount to be allocated to this agent). We propose two different approaches: the benefit-sharing and costs-sharing models. In the first model the endowment is the benefit obtained from cooperation when the minimum cost spanning tree is built and agents’ claims are the difference between their cheapest cost of connecting to the source and their cheapest connection cost. The alternative model establishes that individuals initially pay the cost of their cheapest connection. Then, the endowment is the additional cost that must be satisfied to cover the cost of the efficient tree, being the claims defined as in the previous model. Although both models provide different points of view, we will show that no matter which view you choose, since both approaches provide the same family of allocations for sharing the minimum cost of the network.

Even though both mcst and claims problems involve a population of n agents, their dimensionalities are very different. In a minimum cost spanning tree problem, there is a source $\omega$, and the problem is defined by the costs for connecting every individual to the source; thus a minimum cost spanning tree problem is determined by $(n+1)n/2$ numbers. In a claims problem, there is an endowment and a claim for each agent; thus a claims problem is determined by $n+1$ numbers. Therefore, translating a minimum cost spanning tree problem into a claims problem involves some “loss of information” and there are many ways to proceed.

On the other hand, this translation benefits from the simplicity and tradition of claims rules (equal gains, equal losses, proportional gains/losses, etc.), that might be found in the rich literature which originated with the seminal paper by (O’Neill 1982).

In real-world situations, when there is a conflict of interest in carrying out a joint project, the simplicity of the solution is important for the agents to reach an agreement. In this sense, our proposal has the appeal of an easy and intuitivemechanism to convince the agents involved in the joint project about the equity of the solution.

Our proposal provides a bridge between the literature on claims problems and that on sharing the cost in network problems. As far as we know, only Driessen (1994) links both problems, although he analyzes the other way: transforms a claims problem in a minimum cost spanning tree problem.

The paper is organized as follows. In the next section we present both the minimum cost spanning tree problem and the claims problem. Section 3 introduces the two mentioned approaches to associate a claims problem with a minimum cost spanning tree situation and we prove that both models provide the same family of allocations. In Sect. 4 we discuss some properties of the allocations provided by our model. Section 5 analyzes the coalitional stability of the proposed allocations. Some final comments in Sect. 6 conclude the paper.

2 Preliminaries

2.1 Minimum cost spanning tree problem

A minimum cost spanning tree (hereafter mcst) problem involves a finite set of agents, $N=\{1,2,\ldots ,n\},$ who need to be connected to a source $\omega .$ We denote by $N_{\omega }$ the set of agents and the source and the elements in $N_{\omega }$ are called nodes. There is an undirected complete graph connecting the nodes in $N_{\omega }.$ Any pair of nodes, $i,j \in N_{\omega }$, $i\ne j,$ are connected by an edge $e_{ij} = (i,j)$ and $c_{ij}\in {\mathbb {R}}_{+}$ represents the cost of direct link, the arc $e_{ij}$, between any pair of nodes $i,j \in N_{\omega }.$ We denote by ${\mathbf {C}} = [c_{ij}]$ the symmetric cost matrix, where $c_{ii} =0$, for all $i \in N_{\omega }$. The mcst problem is represented by the pair $(N_{\omega },{\mathbf {C}})$, and the goal is to connect all the agents to the source (directly or through other agents) in the cheapest possible way. The solution to this problem, widely studied, is obtained by means of a spanning tree.

A network over $N_{\omega }$ is any subset of $N_{\omega } \times N_{\omega }$. A spanning tree over $N_{\omega }$ is a network p with no cycles that connects all elements of $N_{\omega }.$ We denote by ${\mathcal {P}}(N_{\omega })$ the set of all spanning trees over $N_{\omega }$. We can identify any spanning tree with a predecessor map $p:N \rightarrow N_{\omega }$ so that $j=p(i)$ is the agent (or the source) to whom i connects in her way towards the source. This map p defines the edges $e^p_{i} = (i,p(i))$ in the tree. In a spanning tree each agent is connected to the source $\omega$, either directly, or indirectly through other agents. Moreover, given a spanning tree p,  there is a unique path from any agent i to the source given by the arcs $(i, p(i)), (p(i), p^2(i)), \ldots , (p^{t-1}(i), p^t(i) = \omega ),$ for some $t \in {\mathbb {N}}.$ The cost of building the spanning tree p is the sum of the cost of the arcs in this tree:

$$\begin{aligned} C_p = \sum _{i=1}^{n}c_{ip(i)}. \end{aligned}$$

Prim (1957) provides an algorithm which solves the problem of connecting all the agents to the source such that the total cost of the network is minimum.¹ This optimal tree may not be unique. Denote by m a spanning tree with minimum cost and by $C_{m(N_{\omega },{\mathbf {C}})}$ its cost (in what follows, when there is no confusion, we simply write $C_m$). That is, for all spanning tree $p \in {\mathcal {P}}(N_{\omega })$

$$\begin{aligned} C_m = \sum _{i=1}^{n}c_{im(i)}\le C_p = \sum _{i=1}^{n}c_{ip(i)}. \end{aligned}$$

A game with transferable utility, TU game, is a pair (N, v) where N is the set of agents and $v : 2^N \rightarrow {\mathbb {R}}$ is known as the characteristic function and it satisfies $v(\varnothing ) = 0$. Sh(N, v) denotes the Shapley value (Shapley 1953) of (N, v). Bird (1976) associated a TU game $(N,v^-)$ to each mcst problem $(N_{\omega }, {\mathbf {C}})$ defining for each coalition $S \subseteq N$, $v^- (S) = C_{m(S_{\omega },{\mathbf {C}})}$; that is, the cost of the optimal spanning tree when only agents in S are involved. This is known as the property rights approach, because the agents in S assume that the rest of the players are not present, or that they cannot use the connections of agents outside S to lower the cost.

Through this work we will follow an alternative approach in which it is assumed that agents in a coalition S can connect the source through agents outside this coalition. This context is known as non-property rights. In this case, the characteristic function is defined by $v^+(S) = \min \left\{ v^-(T): S \subseteq T\right\}$. As pointed out in Bogomolnaia and Moulin (2010), the core of the non-property rights cooperative game $(N,v^+)$ is included in the corresponding core of the TU game $(N,v^-)$. Therefore, our approach is more demanding in terms of coalitional stability.

Once a minimum cost spanning tree m is selected, an important issue is how to allocate the cost $C_m$ among the agents, that is defined by means of a sharing rule (or simply, a solution). In order to define a sharing rule it is important to decide if members of a coalition can freely connect the source through individuals outside their coalition. In our non-property rights approach the non-negativity in the agents’ allocations is a natural requirement (see Bogomolnaia and Moulin (2010)). Then, a sharing rule $\alpha$ is a function that proposes for any mcst problem $(N_{\omega }, {\mathbf {C}})$ an allocation

$$\begin{aligned} \alpha (N_{\omega }, {\mathbf {C}}) = (\alpha _1, \alpha _2, \ldots , \alpha _n) \in {\mathbb {R}}_+^n, \text {such that} \sum _{i=1}^n \alpha _i = C_m. \end{aligned}$$

Among the mentioned sharing rules in mcst problems, Bird, Folk and Serial solutions are non-negative. We will compare our proposals with these solutions.

The Bird rule (Bird 1976) (B) is defined for each $i \in N$ as $B_i ((N_{\omega }, {\mathbf {C}})) = c_{im(i)}.$ As mentioned in Bergantiños and Vidal-Puga (2007) the idea of this rule is simple: agents connect sequentially to the source following Prim’s algorithm and each agent pays the corresponding connection cost. The Serial rule (Moulin and Shenker 1992) (S) proposes to distribute the cost of each arc among the individuals that actually use it in her (unique) path joining the source. In both cases, if there are more than one spanning tree minimizing the total cost, then the solutions propose the average of the corresponding sharing in all these trees. Finally, the Folk rule (Feltkamp et al. 1994; Bergantiños and Vidal-Puga 2007) (F) assigns to each agent $i \in N$ the amount given by the Shapley value of the non-property rights cooperative game, $F_i ((N_{\omega }, {\mathbf {C}})) = Sh(N,v^+)$.

2.2 Claims problems

Given a finite set of agents $N=\left\{ 1,2, \ldots ,n\right\} ,$ a claims problem appears when some endowment should be distributed among these individuals, who demand more than what is available. It is formally defined by a vector $(E,d)\in {\mathbb {R}}_{+}\times {\mathbb {R}}_{+}^{n},$ where E denotes the endowment and d is the vector of agents’ demands, such that the agents’ aggregate demand is greater than or equal to the endowment, $\sum_{i\in N}d_{i} \ge E.$

A claims rule $\varphi$ is a function that associates with each claims problem (E, d) a distribution of the total endowment among the agents (efficiency), such that no agent is allocated neither a negative amount (non-negativity), nor more than their claim (claim-boundedness):

$$\begin{aligned} 0 \le \varphi _i(E,d) \le d_i \forall i \in N, \qquad \sum _{i=1}^n \varphi _i(E,d) = E. \end{aligned}$$

Many claims rules have been proposed in the literature (see Thomson (2019) for formal definitions, properties and references), among which it is worth mentioning the Proportional (Pr), the Constrained Equal Awards (Cea), the Constrained Equal Losses (Cel), or the Talmud (T). These solutions are defined as: for each claims problem (E, d), let R denote the sum of the agents’ claims, $R=\sum_{i\in N} {d_{i}}.$ Then, for all $i \in N$, the above mentioned claims rules are defined as:

• $Pr_i(E,d) = \frac{E}{R} d_i$.

• $Cea_i(E,d) = \min \left\{ d_i,\lambda \right\}$, where $\lambda$ is selected such that $\sum _{i \in N} Cea_i(E,d) = E$.

• $Cel_i(E,d) = \max \left\{ d_i - \mu , 0 \right\}$, where $\mu$ is selected such that $\sum _{i \in N} Cel_i(E,d) = E$.

• $T_i(E,d) = Cea_i\left( \min \left\{ E, \frac{1}{2} \ C\right\} , \frac{1}{2}c\right) + Cel_i\left( \max \left\{ 0, E - \frac{1}{2} \ C\right\} , \frac{1}{2}c\right)$.

A way to address this kind of situations is by analyzing the part of the individuals’ demand that is not satisfied. Specifically, given a claims problem (E, d),  the dual problem (L, d) is defined by focusing on the losses the agents have with respect to their claims, where L denotes the total loss the agents incur, $L=R-E.$ Given a claims rule $\varphi ,$ its dual rule $\varphi ^D$ shares losses in the same way that $\varphi$ shares gains (Aumann and Maschler 1985):

$$\begin{aligned} \varphi ^D_i(L,d) = d_i - \varphi _i(E,d), \quad i=1,2,\ldots ,n. \end{aligned}$$

The Cea and Cel rules are dual of each other. A claims rule $\varphi$ is self-dual if $\varphi ^D = \varphi$. The Proportional and Talmud rules are self-dual.

3 Mapping mcst problems into claims problems

As aforementioned, we aim to define a mapping ${\mathcal {M}}$ that associates mcst situations with claims problems under two alternative approaches.

• The benefit-sharing approach considers that each individual is initially allocated her maximum possible rational cost, that is, fully paying her cheapest way to connect to the source (rational individuals would never pay more than this cost, since agents’ goal is to connect the source at the minimum possible cost). Then, the savings obtained through cooperation are distributed among the individuals. Our argument is as follows:

  As individuals want to be connected to the source, they are willing to pay the cost of their connection to the source. In total, an amount that we denote by $C_{\omega }$ is contributed. But those funds are not yet used, and the network is not yet built. Then, as the network will be common owned, agents want their connections in the optimal network to be their cheapest ones and claim to reduce their contribution to this minimum amount, and demand the extra cost $d_{i*}$, to be returned. If agents agree to cooperate, then everybody can be connected with a total cost of $C_m$ and a network might thus be built for this amount. The benefit of cooperation is $E = C_{\omega } - C_m$. Finally, if the agents agree on how the benefit of cooperation is shared, the minimum cost spanning tree is built.

  Then, the pair $(E,d_*)$ clearly defines a claims problem.

• The cost-sharing approach proposes that individuals pay initially the cost of their cheapest connection. The remaining cost (whenever the cheapest connections do not define a spanning tree) is then distributed among the individuals. Under this approach the argument is as follows:

  In order to provide a common network, individuals are asked for an initial contribution that equals their minimum connection cost. But those funds, $C^{\min }$, are not enough to connect all individuals to the source, and the network is not yet built. If the agents agree to cooperate, then everybody can be connected with a total cost of $C_m$ and a network might thus be built. The additional cost that remains to be distributed is the difference$E_o = C_m - C^{\min }$. Now agents may connect to the source, and their extra contribution cannot be greater than the difference between their connection cost to the source and their minimum connection cost, that we have denoted by $d_{i*}$. Finally, if the agents agree on how the additional cost is distributed, the minimum cost spanning tree is built.

  Then, the pair $(E_o,d_*)$ clearly defines a claims problem.

In both models the claim of each individual is determined by

$$\begin{aligned} d_{i_*} \equiv c_{i \omega }^{*} - c_{i_*} \quad \text {for all} \, i \in N, \quad d_*=(d_{1_*},d_{2_*},\ldots , d_{n_*}), \quad c_{i_*} = \min _{j \in N_{\omega }, j \ne i} \left\{ c_{ij} \right\} ,\\ c^*_{i \omega } = \min _{P_{i \omega }} \left\{ \sum _{e \in P_{i\omega }} c(e) \right\} \qquad P_{i\omega }: \text {path joining agent} i \text {with the source} \omega . \end{aligned}$$

Note that the actual cost for individuals to connect to the source is $c_{i \omega }^{*}$, since they can choose to use their direct connection edge $(i,\omega )$ or to use any path $P_{i\omega }$. We will refer to $c_{i \omega }^{*}$ as the individual i’s rational connection cost to the source.

3.1 Model 1: sharing the benefit of cooperation

We consider throughout this sub-section that the starting points are the rational connection cost to the source, $c_{i \omega }^{*},$ the most an individual is willing to pay. If a minimum cost spanning tree with cost $C_m$ is implemented, the benefit of cooperation $E = C_{\omega } - C_m,$ $C_{\omega } = \sum _{i \in N} c_{i \omega }^{*},$ shall be returned. We assume that no individual will pay less than their minimum connection cost, so the claim $d_{i_*}$ represents the amount they request to be returned from their initial payment $c_{i \omega }^{*}.$ Then, we define a map ${\mathcal {M}}^1$ associating to any mcst problem $(N_{\omega }, {\mathbf {C}})$ the claims problem ${\mathcal {M}}^1(N_{\omega }, {\mathbf {C}})=(E,d_*)$, where $E = C_{\omega } - C_m$ and $d_{i_*} = c_{i \omega }^{*} - c_{i*}$.

Definition 1

For any claims rule $\varphi$ the associated-1 sharing rule for mcst problems $\kappa _1^{\varphi }$ is defined for any mcst problem $(N_{\omega }, {\mathbf {C}})$ and all $i \in N$ by:

$$\begin{aligned} (\kappa _1^{\varphi })_i(N_{\omega }, {\mathbf {C}}) = c_{i \omega }^{*} - \varphi _i({\mathcal {M}}^1(N_{\omega }, {\mathbf {C}})). \end{aligned}$$

As previously mentioned, a claims rule fulfills non-negativity, which has a natural interpretation in the mcst context: no individual should be allocated an amount greater than their rational connection cost to the source; and claim-boundedness meaning that no individual should be allocated an amount below their cheapest connection cost.

3.2 Model 2: sharing the extra cost

We now consider that individuals initially pay their corresponding minimum connection cost $c_{i_*},$ so the total amount paid is $C^{\min } = \sum _{i \in N} c_{i_*}.$ If a minimum cost spanning tree with cost $C_m$ is implemented, there is an extra cost, $E_o = C_m - C^{\min }$, that must be distributed among the agents. As we assume that no individual can pay more than their rational connection cost to the source, the claim of individual i is $d_{i_*}= c_{i \omega }^{*} - c_{i*}.$ Obviously, this claims problem is well defined, since the aggregated claim exceeds the endowment, $\sum _{i=1}^n d_{i_*} \ge E_o.$ Then , we define a new map ${\mathcal {M}}^2$ associating to any mcst problem $(N_{\omega }, {\mathbf {C}})$ the claims problem ${\mathcal {M}}^2(N_{\omega }, {\mathbf {C}})=(E_o,d_{*})$.

Definition 2

For any claims rule $\varphi$ the associated-2 sharing rule for mcst problems $\kappa _1^{\varphi }$ is defined for any mcst problem $(N_{\omega }, {\mathbf {C}})$ and all $i \in N$ by:

$$\begin{aligned} (\kappa _2^{\varphi })_i(N_{\omega }, {\mathbf {C}}) = c_{i_*} + \varphi _i({\mathcal {M}}^2(N_{\omega }, {\mathbf {C}})). \end{aligned}$$

In Example  1 we compute the allocations obtained by applying our models with different claims rules, and compare them with the ones provided by some mcst sharing rules.

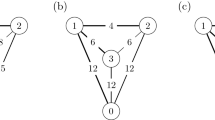
Example 1

Let us consider the mcst problem defined by

Remark 1

Although the direct cost of joining agent 2 to the source is 10 units, under our non-property rights approach the rational cost is 5 units through agent 1. Then, $c^*_{2 \omega } = 5$. Analogously, the rational cost of joining agent 3 to the source $\omega$ is 6 units, $c^*_{3 \omega } = 6$. The rational cost of each arc, when different from the direct cost, appears in brackets in the picture.

The minimum cost spanning tree is given by function m defined as:

$$\begin{aligned} m(1) = \omega \quad m(2) =1 \quad m(3) = 1; \quad C_m =7; \quad C_{\omega } = 15; \quad C^{\min } = 4. \end{aligned}$$

In order to apply claims rules, the benefit of cooperation is $E= C_{\omega } - C_m = 8.$ On the other hand, $c_* = (1,1,2),$ $c^{*} = (4,5,6)$, so the claims are $d_*=(3,4,4),$ and $E_o= 3.$ Table 1 shows the obtained results.

Table 1 Proposals obtained by applying mcst solutions and claims rules in Example 1

We observe that the solutions defined by using the usual claims rules propose reasonable allocations of the total cost. The Serial solution is retrieved (in this example) through the Cea or Cel claims rules. We also note that $\kappa _1$ and $\kappa _2$ coincide when applied to Proportional or Talmud rules. This is a direct consequence of duality properties in claims rules, since these rules are self-dual, and it is formally established in the following result.

Proposition 1

For any mcst problem $(N_{\omega }, {\mathbf {C}}) \in {\mathcal {N}}_n$ and any claims rule $\varphi ,$

$$\begin{aligned} \kappa _1^{\varphi }(N_{\omega }, {\mathbf {C}}) = \kappa _2^{\varphi ^D}(N_{\omega }, {\mathbf {C}}). \end{aligned}$$

Proof

Let us consider the associated claims problems

$$\begin{aligned} (E,d_*) = {\mathcal {M}}^1(N_{\omega }, {\mathbf {C}}), \quad (E_o,d_*) = {\mathcal {M}}^2(N_{\omega }, {\mathbf {C}}). \end{aligned}$$

By definition of $\varphi ^D$,

$$\begin{aligned} \varphi _i(E,d_*) = d_{i_*} - \varphi _i^D\left( \sum _{i \in N} d_{i_*} - E, d_* \right) = d_{i_*} - \varphi _i^D(E_o, d_*). \end{aligned}$$

Then,

$$\begin{aligned} (\kappa _1^{\varphi })_i(N_{\omega }, {\mathbf {C}}) &= c_{ii}^{*} - \varphi _i(E,d_*) = c_{ii}^{*} - \left( d_{i_*} - \varphi _i^D(E_o, d_*) \right) \\ = c_{i_*} + \varphi _i^D(E_o, d_*) &= (\kappa _2^{\varphi ^D})_i(N_{\omega }, {\mathbf {C}}) \end{aligned}$$

and duality is obtained. $\square$

Consequently we obtain that if a claims rule $\varphi$ is self dual, for any mcst problem $(N_{\omega }, {\mathbf {C}})$ both models propose the same distribution of the total cost.

$$\begin{aligned} \kappa _1^{\varphi }(N_{\omega }, {\mathbf {C}}) = \kappa _2^{\varphi }(N_{\omega }, {\mathbf {C}}). \end{aligned}$$

In particular, the Proportional or Talmud rules provide the same allocation with both models.

Therefore, the two models propose the same family of cost allocations. Then, hereinafter we will only analyze the model defined by ${\mathcal {M}}^1.$

4 Properties

Bergantiños and Vidal-Puga (2007) provide a very exhaustive normative study on the solutions of mcst problems. They present a list of properties that a solution should satisfy and compare, among others, the Bird and Folk solutions in terms of the properties that satisfy.²

In this section we analyze if some of these properties are fulfilled by the solutions we have defined through claims rules. The property of coalitional stability (core selection) is analyzed in the next section. We first briefly introduce the properties.

Individual Rationality: A sharing rule $\alpha$ for mcst problems satisfies Individual Rationality if for each problem $(N_{\omega }, {\mathbf {C}}),$ and all $i \in N,$ $\alpha _i (N_{\omega }, {\mathbf {C}})_i \le c_{i\omega }^{*}.$

Continuity: A solution $\alpha$ for mcst problems satisfies Continuity if $\alpha$ is continuous function of the cost matrix ${\mathbf {C}}$.

Positivity: A solution $\alpha$ for mcst problems satisfies Positivity if for each problem $(N_{\omega }, {\mathbf {C}}),$ and all $i \in N,$ then $\alpha _i (N_{\omega }, {\mathbf {C}}) \ge 0.$

Symmetry: A solution $\alpha$ for mcst problems satisfies Symmetry if for each problem $(N_{\omega }, {\mathbf {C}}),$ whenever individuals $i, j \in N$ are such that $c_{ik} = c_{jk},$ for all $k \in N_{\omega },$ then $\alpha _i (N_{\omega }, {\mathbf {C}}) = \alpha _j(N_{\omega }, {\mathbf {C}}).$

Cost Monotonicity: A solution $\alpha$ for mcst problems satisfies Cost Monotonicity if for any two problems $(N_{\omega }, {\mathbf {C}}),$ $(N_{\omega }, \mathbf {C^{\prime }}),$ such that $c_{i j} < c^{\prime }_{i j}$ for some $i \in N$, $j \in N_{\omega }$ and $c_{kl} =c^{\prime }_{kl}$ otherwise, $\alpha _i (N_{\omega },{\mathbf {C}}) \le \alpha _i (N_{\omega },\mathbf {C^{\prime }})$.

It is clear that, for any claims rule $\varphi$, our proposal fulfills these properties.

Proposition 2

For any claims rule $\varphi$ the solution $\kappa _1^{\varphi }$ satisfies Individual Rationality, Continuity and Positivity. In addition, $\kappa _1^{\varphi }$ satisfies Symmetry if the claims rule is symmetric and satisfies Cost monotonicity if the claims rule is claims monotonic.³

An additional property that has been considered for solutions of mcst problems is:

Population Monotonicity: A solution $\alpha$ for mcst problems satisfies Population Monotonicity if for each problem $(N_{\omega }, {\mathbf {C}}),$ and all $S \subset N$, $\alpha _i (N_{\omega },{\mathbf {C}}) \le \alpha _i (S_{\omega },{\mathbf {C}})$ for all $i \in S$.

The following example shows that $\kappa _1^{\varphi }$ does not fulfill this property.

Example 2

Let us consider the mcst problem with $n=5$ individuals depicted in the following figure (as the graph should be complete, we consider that the costs of the arcs not shown are all equal to 10).

There are several trees with minimum cost. We consider

$$\begin{aligned} m(1) = \omega \quad m(2)= 1 \quad m(3) = 4 \quad m(4) = 5 \quad m(5) = \omega \end{aligned}$$

Throughout easy computations we obtain $C_m=2$, $C_{\omega }=5$, $E=3$, and the claims vector $d_*=(1,1,1,1,1).$ Therefore, for any (anonymous) claims rule $\varphi$

$$\begin{aligned} (\kappa _1^{\varphi })_i = c_{i \omega }^{*} - \dfrac{E}{5} = \dfrac{2}{5}, \qquad i=1,2,3,4,5 \end{aligned}$$

If we consider the coalition $S = \left\{ 3,4,5\right\}$ and the mcst problem $(S_{\omega },{\mathbf {C}})$, our model allocates $\frac{1}{3}$ to each agent in S (for any anonymous claims rule), contradicting Population monotonicity.

5 Coalitional stability

In a mcst problem, cooperation is necessary in order to implement the optimal tree. Then, coalitional stability is required to prevent that groups of individuals may have incentives to build their own network and then a minimum cost spanning tree would not be implemented. To this end, a cooperative game associated with a mcst problem has been introduced so that, for each coalition $S \subseteq N,$ the characteristic function represents the cost of connecting all individuals in this coalition to the source. Formally, given the mcst problem $(N_{\omega }, {\mathbf {C}})$ and a coalition $S \subseteq N,$ the (monotonic) cost of connecting this coalition to the source is (in our non-property context):

$$\begin{aligned} v(S) = \min \left\{ C_m(T): \, S\subseteq T \subseteq N \right\} \end{aligned}$$

where $C_m(T)$ is the cost of the efficient tree of the problem $(T_{\omega }, {\mathbf {C}}\vert _T).$ The core associated to a mcst problem is then defined by:

$$\begin{aligned} co(N_{\omega }, {\mathbf {C}}) = \left\{ \alpha \in {\mathbb {R}}^n : \sum _{i \in S} \alpha _i \le v(S), \quad \forall S \subseteq N, \quad \sum _{i \in N} \alpha _i = v(N) = C_m \right\} . \end{aligned}$$

In Example 1 the characteristic function is:

$$\begin{aligned} v(\{1\}) = 4; \, v(\{2\}) = v(\{1,2\}) = 5; \, v(\{3\}) = v(\{1,3\}) = 6; \, v(\{2,3\}) = v(\{1,2,3\}) = 7. \end{aligned}$$

Although all the allocations we obtained in this example (Table 1) belong to the core, this is not true in general. In Example 2, the total amount allocated to coalition S is 6/5, which is greater than $v(S) = 1$. So, no allocation in the core can be obtained in this example by using (anonymous) claims rules throughout our approach.

The following result shows a necessary and sufficient condition, in terms of the mcst cost matrix, ensuring that the allocation provided by $\kappa _1^{\varphi }$ belongs to the core of the monotonic cooperative game, regardless of the claims rule $\varphi$ used in its definition.

Theorem 1

Given a mcst problem $(N_{\omega }, {\mathbf {C}})$, if

$$\begin{aligned} C_m - \sum _{i \notin S} c_{i*} \le v(S) \quad \text { for all } S \subseteq N \text { such that } v(S) \ne \sum _{i \in S} c_{i \omega }^{*} \end{aligned}$$

(1)

for any claims rule $\varphi$ the allocation $(\kappa _1^{\varphi })_i(N_{\omega }, {\mathbf {C}}) = c_{i \omega }^{*} - \varphi _i(E,d_*),$ $i \in N,$ belongs to the core of the monotonic cooperative game associated with the mcst problem. Conversely, if for any claims rule $\varphi ,$ the allocation $(\kappa _1^{\varphi })(N_{\omega }, {\mathbf {C}})$ belongs to the core, Condition (1) is fulfilled.

Proof

First we consider $S \subseteq N$ such that $v(S) \ne \sum _{i \in S} c_{i \omega }^{*}$. We need to prove that, for any claims rule $\varphi$,

$$\begin{aligned} \sum _{i \in S} (\kappa _1^{\varphi })_i(N_{\omega }, {\mathbf {C}}) \le v(S). \end{aligned}$$

We know that any claims rule $\varphi$ satisfies non-negativity and claim-boundedness, which implies that for all $S \subseteq N,$

$$\begin{aligned} \sum _{i \in S} \varphi _i(E,d_*) \ge \max \left\{ E - \sum _{i \notin S} d_{i_*}, 0 \right\} . \end{aligned}$$

Note that $E - \sum _{i \notin S} d_{i*} = \sum _{i \in S}c_{ii}^{*} + c_{i*} - C_m$ and then

$$\begin{aligned} \sum _{i \in S} (\kappa _1^{\varphi })_i(N_{\omega }, {\mathbf {C}}) &= \sum _{i \in S} c_{i \omega }^{*} - \sum _{i \in S} \varphi _i(E,d_*) \le \sum _{i \in S} c_{i \omega }^{*} - \max \left\{ E - \sum _{i \notin S} d_{i_*}, 0 \right\} \\ &\le \sum _{i \in S} c_{i \omega }^{*} - \left( E - \sum _{i \notin S} d_{i_*} \right) = C_m - \sum _{i \notin S} c_{i*} \le v(S) \end{aligned}$$

from Condition (1). Let us consider now a coalition $S \subseteq N$ such that $v(S) = \sum _{i \in S} c_{i \omega }^{*}$. As $\left( \kappa _1^{\varphi }\right) _i \le c_{i \omega }^{*}$, obviously $\sum _{i \in S} (\kappa _1^{\varphi })_i(N_{\omega }, {\mathbf {C}}) \le v(S).$ So, for any claims rule $\varphi$, $\kappa _1^{\varphi }$ is in the core of the monotonic cooperative game.

Conversely, let us suppose that for some coalition $S \subseteq N$, $v(S) \ne \sum _{i \in S} c_{i \omega }^{*}$ and $C_m - \sum _{i \notin S} c_{i*} > v(S).$ Consider the constrained dictatorial claims rule, $\varphi ^{CD}$, in which the first agents to receive their claims are those outside S; that is, we consider a permutation $\pi$ such that $\pi (1), \pi (2), \ldots , \pi (n-s) \notin S$, where s denotes the number of agents in S. Under our model, the claims rule provides the cost allocation $\alpha _i = c_i^{*} - \varphi ^{CD}_i(E,d_*)$, $\sum _{i \in N} \alpha _i = C_m.$ If we analyze the endowment E and the demands of agents not in S, we obtain two possibilities:

• (a) $E \ge \sum _{i \notin S} d_{i*}$; or       (b) $E < \sum _{i \notin S} d_{i*}$

In the first case, $\varphi ^{CD}_i(E,d_*) = d_{i*}$, so $\alpha _i = c_{i*}$ for all $i \notin S$. Then,

$$\begin{aligned} \sum _{i \in S} \alpha _i = C_m - \sum _{i \notin S} c_{i*} > v(S) \end{aligned}$$

and the allocation is not in the core.

The second case implies $\varphi ^{CD}_i(E,d_*) = 0$, so $\alpha _i = c_{i \omega }^{*}$ for all $i \in S$. This allocation only can be in the core if $v(S) = \sum _{i \in S} c_{i \omega }^{*}$, a contradiction. So, the allocation is neither in the core in this case. $\square$

Checking Condition (1) may require as much calculus as directly testing that the allocation provided is in the core. Nevertheless, it is important to emphasize that this condition only depends on the data of the mcst problem and once it is checked, it remains valid for any claims rule. In order to interpret Condition (1), it says that, for any coalition S, there is some chance of obtaining benefits from cooperation even in the case that individuals outside S pay only their minimum connection cost (the minimum they can pay under our approach); or, all members in S pay her rational connection to the source, which is at the same time their minimum connection cost.

The sufficient and necessary condition obtained to guarantee coalitional stability may seem quite technical. However, it is useful from an operational point of view, since it allows us to identify sub-classes of mcst problems where the solution we propose is always a core selection, for every claims rule.

5.1 Some special classes of mcst problems

In this section we show some classes of mcst problems so that Condition (1) is always fulfilled and the allocation $\kappa _1^{\varphi }(N_{\omega }, {\mathbf {C}})$ belongs to the core of the monotonic cooperative game, for any claims rule $\varphi .$

5.1.1 $2-$ mcst problems

Let us consider the so-called $2-$mcst problems (Estévez-Fernández and Reijnierse 2014; Subiza et al. 2016) in which the connection cost between two different individuals (houses, villages, ...) can only take one of two possible values (low and high cost). Moreover, we consider problems $(N_{\omega }, {\mathbf {C}})$ such that $c_{ij} = k_1,$ $i,j \in N$, $i \ne j,$ $c_{i \omega } = k_2,$ with $0 \le k_1 \le k_2.$ It is easy to check that Condition (1) is fulfilled. Our model proposes, for any claims rule $\varphi ,$ the allocation

$$\begin{aligned} (\kappa _1^{\varphi })_i (N_{\omega }, {\mathbf {C}})= k_2 - \dfrac{n-1}{n} (k_2 - k_1) \qquad i = 1,2, \ldots , n, \end{aligned}$$

which belongs to the core (it coincides with the Folk solution).

5.1.2 Information graph games

A related scenario appears when analyzing information graph games (Kuipers 1993). This games can be formalized in the following way.

A set of customers N are all interested in a particular piece of information. A subset Z of N, called the informed set, already possesses this information. Other customers may purchase the information from a central supplier for a fixed price, say 1, or they may share the information with a friendly customer, who already has the information.

This situation can be represented by an undirected graph and the information graph game in a minimum cost spanning tree problem, where the cost of an arc is 0 or 1, by depending if one of the agents in the arc belong to Z. In this case, set N can be decomposed in disjoint components, $N = \left( \bigcup _{t=1}^{r} U_t \right) \bigcup \left( \bigcup _{t=1}^{s} C_t \right)$, such that:

• 1. For each $i \in U_t$, $|U_t| = 1$, $c_{i*} = c^{*}_{i\omega } =1.$

• 2. For each $i \in U_t$, $|U_t| > 1$, $c_{i*} = 0$, $c^{*}_{i\omega } =1.$

• 3. For each $i \in C_t$, $c_{i*} = c^{*}_{i\omega } =0.$

Now, for each coalition $S \subseteq N$, if S intersects k components of type $U_t$, $v(S) \ge k$ and $\sum _{i \notin S} c_{i*} \ge r -k$, whereas $C_m = r$. Therefore, condition (1) holds and, for any claims rule $\varphi$, the solution $\kappa _1^{\varphi }$ is in the core of the cooperative game.

5.1.3 Linear mcst problems

Another focal class of mcst problems in which Condition (1) is always satisfied is given by linear msct problems. Let us consider a group of individuals $N= \{1,2,\ldots ,n \}$ situated in a row that wish to connect to a source $\omega$. The cost of connecting one individual with the next one is 1 unit. If an individual wants to connect to the source, she must do it through all its neighbors on the way towards the source and pay all costs.

Formally, for each $i,j \in N,$ $i \ne j,$ the connection cost is $c_{ij} = |i-j|.$ For each $i \in N,$ the cost to the source is $c_{i \omega } = i.$

The minimum cost spanning tree connects each individual to the next, and the first one with the source, with a total cost $C_m = n.$ It is easy to observe that Condition (1) is fulfilled, since for all $S \subseteq N$, $|S| = s$,

$$\begin{aligned} C_m = n, \qquad \sum _{i \notin S} c_{i*} = n-s, \qquad v(S) = \max \left\{ i \in S \right\} \ge s. \end{aligned}$$

5.1.4 Bipersonal mcst problems

If there are just $n=2$ agents

it is not hard to prove that Condition (1) is fulfilled. Moreover, in this case, it can be proved that the Folk solution is obtained with our model, if we use the Talmud claims rule; that is,

$$\begin{aligned} \kappa _1^{T}(N_{\omega }, {\mathbf {C}}) = F(N_{\omega }, {\mathbf {C}}). \end{aligned}$$

5.2 Modifying the claims vector

Up to this point, we have fixed an estate E, the benefit of cooperation, and a vector of claims $d_*$ in order to apply our model. It is clear that other possibilities when defining the claim of each agent can be considered. The following result shows that the selection of the claims vector influences that the final allocation belongs to the core.

Proposition 3

Let us consider a mcst problem $(N_{\omega }, {\mathbf {C}}).$ Let $E = C_{\omega } - C_m$ be the benefit of cooperation and let $c_{\omega } = \left( c_{1\omega }^*, c_{2\omega }^*, \ldots , c_{n\omega }^* \right)$ be the vector of rational costs to the source. Then, there exists a claims vector ${\hat{d}},$ such that for any claims rule $\varphi$, $\kappa ^{\varphi } (N_{\omega }, {\mathbf {C}}) = c_{\omega } - \varphi (E,{\hat{d}}) \in co(N_{\omega }, {\mathbf {C}}).$

Proof

To show the existence of the required claims vector, for each $i \in N,$ consider ${\hat{d}}_i = c_{i\omega }^{*} - c_{im(i)}.$ Then, $\sum _{i \in N} {\hat{d}}_i = E,$ so $(E, {\hat{d}})$ is a degenerated claims problem and for any claims rule $\varphi$, $\varphi _i(E, {\hat{d}}) = {\hat{d}}_i$ and agent i is allocated the amount $\alpha _i = c_{im(i)}$, which is in the core of the cooperative game and coincides with the Bird solution if the minimum cost spanning tree is unique. $\square$

6 Final comments

The current paper explores a bridge between two independent problems that have been extensively analyzed in the literature: minimum cost spanning tree and claims problems. Specifically, we present new ways of allocating the cost of a network that are based on claims rules that share the benefit of cooperation. It is noteworthy that in our approach only two costs are used: the rational cost to the source and the cost to the cheapest edge (also the costs $c_{im(i)}$ are used in order to compute $C_m$, the cost of the efficient tree). The aforementioned feature (ignoring most of the available information) links our proposals with the so-called reductionism approach (Bogomolnaia and Moulin 2010).

Our approach allows for easy and intuitive ways to distribute the cost of an optimal network among the involved agents. For instance, when using the proportional claims rule, our model proposes a proportional sharing of the benefit of cooperation, or a proportional distribution of the extra-cost. Analogously, when using egalitarian claims rules, we propose an equal sharing of the benefit of cooperation, or an equal sharing of the extra-cost (subject that no agent pay more that their individual cost, nor a negative amount). Only the Bird, or Serial solutions are such easier methods. Nevertheless, the Bird solution can be seen as unfair and the Serial may propose for an agent a payment greater than its direct connection to the source. Let us observe the following example:

Then, $C_m = 160$ and the Bird proposal is $B=(100,60)$ (each agent pays their own connection); so, agent 1 does not obtain any gains from cooperation. The Serial solution is $S=(50,110)$; so, agent 2 pays more than connecting directly to the source. The Folk solution proposes an equal sharing of the cost, $F=(80,80).$ Our model proposes the following allocations, depending on the used claims rules:

$$\begin{aligned} \kappa _1^{Pr} = (78.8,81.2) \qquad \kappa _1^{Cea} =(77.5,77.5) \qquad \kappa _1^{Cel} = \kappa _1^{T} = (80,80) \end{aligned}$$

As mentioned, a drawback of our proposal is that sometimes it fails to propose core allocations. A possible way to prevent coalitions leaving the group is to find the core allocation closest to our selected proposal (see Giménez-Gómez et al. (2020)). For instance, if the proportional criteria is assumed, and $\kappa _1^{Pr}$ is not in the core, then we can obtain the allocation x in the core minimizing the distance $d(x,\kappa _1^{Pr})$, although we lose the simplicity and intuitive idea of the solution.