1 Introduction

Nonlinear evolution equations (NLEEs) have been used to describe certain nonlinear phenomena in, e.g., fluid mechanics, condensed matter physics, plasma physics, elastic mechanics, particle physics and optical communication [1,2,3,4,5,6,7,8]. For instance, people have seen a Whitham-Broer-Kaup system describing the dispersive long wave in shallow water [9], a variable-coefficient generalized dispersive water-wave system describing the long weakly-nonlinear and weakly-dispersive surface waves of variable depth in the shallow water [10], a generalized (2+1)-dimensional dispersive long-wave system describing the nonlinear and dispersive long gravity waves in two horizontal directions on the shallow water of an open sea or a wide channel of finite depth [11], a modified dispersive water-wave system describing the nonlinear and dispersive long gravity waves traveling in two horizontal directions on the shallow waters of uniform depth [12], and a Boussinesq-Burgers system describing the propagation of the shallow water waves [13]. Other relevant systems in fluid mechanics have been reported, e.g., in Refs. [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. Studies on the analytic solutions of the NLEEs have provided the insight into the physical aspects of the problems and further applications [30,31,32,33]. In order to obtain different solutions of the NLEEs, such as the solitons, periodic waves, breather waves, travelling waves and rogue waves [34,35,36,37,38,39,40,41,42], methods have been proposed, e.g., the Hirota bilinear method, Pfaffian technique, Bäcklund transformation, Hirota-Riemann method, Darboux transformation and Lie group method [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58].

Lie symmetry method has been applied to the NLEEs to obtain certain symmetry groups, symmetry reductions, analytic solutions and optimal systems of the subalgebras [50, 52, 59, 60]. With a given subgroup, numbers of the independent variables in an NLEE have been reduced, based on which the group-invariant solutions are derived [60].

For the shallow water waves, Refs. [61,62,63,64] have presented a (2+1)-dimensional modified dispersive water-wave system:

$$\begin{aligned} \begin{aligned}&u_{ty}+u_{xxy}-2v_{xx}-2u u_{xy}-2u_{x}u_{y}=0,\\&v_{t}-v_{xx}-2(uv)_{x}=0, \end{aligned} \end{aligned}$$
(1)

where \(u=u(x,y,t)\) indicates the height of the water surface, \(v=v(x,y,t)\) indicates the horizontal velocity of the water wave, and the subscripts denote the partial derivatives with respect to the scaled space variables x, y and time variable t. System (1) has been used to describe the nonlinear and dispersive long gravity waves travelling in two horizontal directions on the shallow water of uniform depth [61,62,63,64]. Residual symmetry and soliton solutions of System (1) have been derived [61]. Non-travelling wave solutions of System (1) have been obtained via the generalized projective Riccati equation method [62]. Soliton-trigonometric waves, soliton-cosine periodic waves, and soliton-cnoidal waves solutions of System (1) have been derived via the consistent Riccati expansion method [63]. Hybrid solutions of System (1) which describe the interactions among the lump, kink soliton and stripe soliton have been derived [64].

Ref. [65] has considered a generalization of System (1) for the shallow water waves:

$$\begin{aligned} \begin{aligned}&u_{ty}+\alpha u_{xxy}-2\alpha v_{xx}-\beta u u_{xy}-\beta u_{x}u_{y}=0,\\&v_{t}-\alpha v_{xx}-\beta (uv)_{x}=0, \end{aligned} \end{aligned}$$
(2)

where \(\alpha \) and \(\beta \) are the nonzero constants, \(u=u(x,y,t)\) denotes the height of the water surface, \(v=v(x,y,t)\) is the horizontal velocity of the water wave, and the subscripts denote the partial derivatives with respect to the scaled space variables x, y and time variable t. Ref. [65] has constructed certain scaling transformations, hetero-Bäcklund transformations and similarity reductions for System (2). When \(\alpha =1\) and \(\beta =2\), System (2) reduces to System (1).

However, to our knowledge, Lie point symmetry generators, Lie symmetry groups and symmetry reductions for System (2) have not been discussed. Hyperbolic-function, trigonometric-function and rational solutions for System (2) have not been investigated via the polynomial expansion, Riccati equation expansion and \(\left( \frac{G^{'}}{G}\right) \) expansion methods. In Sect. 2, the Lie point symmetry generators and Lie symmetry groups for System (2) will be derived. In Sect. 3, symmetry reductions will be obtained through the Lie point symmetry generators. Hyperbolic-function, trigonometric-function and rational solutions for System (2) will be constructed via the polynomial expansion, Riccati equation expansion and \(\left( \frac{G^{'}}{G}\right) \) expansion methods. In Sect. 4, the conclusions will be given.

2 Lie Group Analysis for System (2)

2.1 Lie Point Symmetry Generators for System (2)

Based on the Lie group method [66,67,68,69,70], a one-parameter Lie group of the infinitesimal transformations acting on the independent and dependent variables can be defined as

$$\begin{aligned} \begin{aligned}&{\tilde{x}}=x+\epsilon \xi (x,y,t,u,v)+O(\epsilon ^2),\\&{\tilde{y}}=y+\epsilon \eta (x,y,t,u,v)+O(\epsilon ^2),\\&{\tilde{t}}=t+\epsilon \tau (x,y,t,u,v)+O(\epsilon ^2),\\&{\tilde{u}}=u+\epsilon \phi (x,y,t,u,v)+O(\epsilon ^2),\\&{\tilde{v}}=v+\epsilon \varphi (x,y,t,u,v)+O(\epsilon ^2), \end{aligned} \end{aligned}$$
(3)

where \({\tilde{x}}\), \({\tilde{y}}\), \({\tilde{t}}\), \({\tilde{u}}\), \({\tilde{v}}\), \(\xi \), \(\eta \), \(\tau \), \(\varphi \) and \(\phi \) are the real functions of x, y, t, u and v, \(\epsilon \) is a parameter of the infinitesimal transformation and \(O(\epsilon ^2)\) is the infinitesimal of the same order of \(\epsilon ^2\).

Lie point symmetry generators for System (2) are derived as

$$\begin{aligned} V{} & {} =\xi (x,y,t,u,v)\frac{\partial }{\partial x}+\eta (x,y,t,u,v)\frac{\partial }{\partial y}+\tau (x,y,t,u,v)\frac{\partial }{\partial t}\nonumber \\{} & {} \quad +\phi (x,y,t,u,v)\frac{\partial }{\partial u}+\varphi (x,y,t,u,v)\frac{\partial }{\partial v}, \end{aligned}$$
(4)

where \(\xi \), \(\eta \), \(\tau \), \(\phi \) and \(\varphi \) satisfy the following conditions

$$\begin{aligned} \text {pr}^{(3)}V(E_{1})|_{E_{1}=0}=0,~\text {pr}^{(2)}V(E_{2})|_{E_{2}=0}=0, \end{aligned}$$
(5)

with

$$\begin{aligned} \begin{aligned}&E_{1}=u_{ty}+\alpha u_{xxy}-2\alpha v_{xx}-\beta u u_{xy}-\beta u_{x}u_{y},\\&E_{2}=v_{t}-\alpha v_{xx}-\beta (uv)_{x}. \end{aligned} \end{aligned}$$
(6)

\(\text {pr}^{(3)}V(\cdot )\) and \(\text {pr}^{(2)}V(\cdot )\) denote the third and second prolongation of V, respectively, defined as [67],

$$\begin{aligned} \begin{aligned}&\text {pr}^{(3)}V(\cdot )=\xi \frac{\partial }{\partial x}(\cdot )+\eta \frac{\partial }{\partial y}(\cdot )+\tau \frac{\partial }{\partial t}(\cdot )+\phi \frac{\partial }{\partial u}(\cdot )+\varphi \frac{\partial }{\partial v}(\cdot )+\phi ^{x}\frac{\partial }{\partial u_{x}}(\cdot )\\&\quad {+}\phi ^{y}\frac{\partial }{\partial u_{y}}(\cdot ){+}\phi ^{xy}\frac{\partial }{\partial u_{xy}}(\cdot ){+}\phi ^{ty}\frac{\partial }{\partial u_{ty}}(\cdot ){+}\varphi ^{xx}\frac{\partial }{\partial v_{xx}}(\cdot ){+}\phi ^{xxy}\frac{\partial }{\partial u_{xxy}}(\cdot ),\\&\text {pr}^{(2)}V(\cdot )=\xi \frac{\partial }{\partial x}(\cdot )+\eta \frac{\partial }{\partial y}(\cdot )+\tau \frac{\partial }{\partial t}(\cdot )+\phi \frac{\partial }{\partial u}(\cdot )+\varphi \frac{\partial }{\partial v}(\cdot )+\phi ^{x}\frac{\partial }{\partial u_{x}}(\cdot )\\&\quad +\varphi ^{x}\frac{\partial }{\partial v_{x}}(\cdot )+\varphi ^{t}\frac{\partial }{\partial v_{t}}(\cdot )+\varphi ^{xx}\frac{\partial }{\partial v_{xx}}(\cdot ),\\&\phi ^{x}=D_{x}(\phi -\xi u_{x}-\eta u_{y}-\tau u_{t})+\xi u_{xx}+\eta u_{xy}+\tau u_{xt},\\&\phi ^{y}=D_{y}(\phi -\xi u_{x}-\eta u_{y}-\tau u_{t})+\xi u_{yx}+\eta u_{yy}+\tau u_{yt},\\&\phi ^{xy}=D_{x}D_{y}(\phi -\xi u_{x}-\eta u_{y}-\tau u_{t})+\xi u_{xxy}+\eta u_{xyy}+\tau u_{xyt},\\&\phi ^{ty}=D_{t}D_{y}(\phi -\xi u_{x}-\eta u_{y}-\tau u_{t})+\xi u_{xty}+\eta u_{yty}+\tau u_{tty},\\&\phi ^{xxy}=D_{x}^{2}D_{y}(\phi -\xi u_{x}-\eta u_{y}-\tau u_{t})+\xi u_{xxxy}+\eta u_{xxyy}+\tau u_{xxyt},\\&\varphi ^{t}=D_{t}(\varphi -\xi v_{x}-\eta v_{y}-\tau v_{t})+\xi v_{tx}+\eta v_{ty}+\tau v_{tt},\\&\varphi ^{x}=D_{x}(\varphi -\xi v_{x}-\eta v_{y}-\tau v_{t})+\xi v_{xx}+\eta v_{xy}+\tau v_{xt},\\&\varphi ^{xx}=D_{x}^{2}(\varphi -\xi v_{x}-\eta v_{y}-\tau v_{t})+\xi v_{xxx}+\eta v_{xxy}+\tau v_{xxt},\\ \end{aligned} \end{aligned}$$
(7)

where \(D_{x}\), \(D_{y}\) and \(D_{t}\) are the total derivative operators.

Expanding Expressions (5) and splitting on the derivatives of u and v, we have the following results:

$$\begin{aligned} \begin{aligned}&\tau _{x}=\tau _{y}=\tau _{u}=\tau _{v}=\xi _{u}=\xi _{v}=\xi _{y}=\eta _{x}=\eta _{u} =\eta _{v}=\eta _{t}=\phi _{v}=\varphi _{u}=0,\\&2\xi _{x}-\tau _{t}=0,~\beta [(\xi _{x}-\tau _{t})u-\phi ]-\xi _{t}=0,~\xi _{x}-\tau _{t}-\phi _{u}=0,\\&2\xi _{x}-\varphi _{v}-\tau _{t}-\eta _{y}+\phi _{u}=0,~(\varphi _{v}-\tau _{t}-\phi _{u}+\xi _{x})v-\varphi =0. \end{aligned} \end{aligned}$$
(8)

Solving the system of equations given in (8), we obtain the following results

$$\begin{aligned} \begin{aligned}&\tau =2c_1t+c_4,\\&\xi =c_{1}x+c_{3}\beta t+c_{5},\\&\eta =-(c_{1}+c_{2})y+c_{6},\\&\phi =-c_{1}u-c_{3},\\&\varphi =c_{2}v, \end{aligned} \end{aligned}$$
(9)

where \(c_1\), \(c_2\), \(c_3\), \(c_4\), \(c_{5}\) and \(c_6\) are the real constants. Lie point symmetry generators for System (2) are derived as:

$$\begin{aligned} \begin{aligned}&V_1=\frac{\partial }{\partial x}, ~V_2=\frac{\partial }{\partial t}, ~V_3=\frac{\partial }{\partial y}, ~V_4=v\frac{\partial }{\partial v}-y\frac{\partial }{\partial y},\\&V_{5}=-\frac{\partial }{\partial u}+\beta t\frac{\partial }{\partial x},~V_{6}=x\frac{\partial }{\partial x}+2t\frac{\partial }{\partial t}-y\frac{\partial }{\partial y}-u\frac{\partial }{\partial u}. \end{aligned} \end{aligned}$$
(10)

Motivated by Ref. [68], we show commutation relations among Lie Symmetry Generators (10) in Table 1, where the entries in row I and column J are represented by the commutators \([V_{I}, V_{J}]\), commutators \([V_{I}, V_{J}]\) are defined as [70]

$$\begin{aligned}{}[V_{I}, V_{J}]=V_{I}V_{J}-V_{J}V_{I}, (I,J=1,2,3,4,5,6). \end{aligned}$$
(11)
Table 1 Commutator table of the Lie algebra for System (2)
Full size table

2.2 Lie Symmetry Group for System (2)

In order to obtain the group transformation for System (2), which is produced by the infinitesimal generators \(V_{I}\) \(,I=1,2,3,4,5,6\), we need to solve the initial problems:

$$\begin{aligned}{} & {} \frac{\text {d}{\bar{x}}(\epsilon )}{\text {d}\epsilon }=\xi [{\bar{x}}(\epsilon ),{\bar{y}}(\epsilon ),{\bar{t}}(\epsilon ),{\bar{u}}(\epsilon ),{\bar{v}}(\epsilon )],~{\bar{x}}|_{\epsilon =0}=x,\nonumber \\{} & {} \frac{\text {d}{\bar{y}}(\epsilon )}{\text {d}\epsilon }=\eta [{\bar{x}}(\epsilon ),{\bar{y}}(\epsilon ),{\bar{t}}(\epsilon ),{\bar{u}}(\epsilon ),{\bar{v}}(\epsilon )],~{\bar{y}}|_{\epsilon =0}=y,\nonumber \\{} & {} \frac{\text {d}{\bar{t}}(\epsilon )}{\text {d}\epsilon }=\tau [{\bar{x}}(\epsilon ),{\bar{y}}(\epsilon ),{\bar{t}}(\epsilon ),{\bar{u}}(\epsilon ),{\bar{v}}(\epsilon )],~{\bar{t}}|_{\epsilon =0}=t,\nonumber \\{} & {} \frac{\text {d}{\bar{u}}(\epsilon )}{\text {d}\epsilon }=\phi [{\bar{x}}(\epsilon ),{\bar{y}}(\epsilon ),{\bar{t}}(\epsilon ),{\bar{u}}(\epsilon ),{\bar{v}}(\epsilon )],~{\bar{u}}|_{\epsilon =0}=u,\nonumber \\{} & {} \frac{\text {d}{\bar{v}}(\epsilon )}{\text {d}\epsilon }=\varphi [{\bar{x}}(\epsilon ),{\bar{y}}(\epsilon ),{\bar{t}}(\epsilon ),{\bar{u}}(\epsilon ),{\bar{v}}(\epsilon )],~{\bar{v}}|_{\epsilon =0}=v. \end{aligned}$$
(12)

Then, we can derive the Lie symmetry groups \(g_{I}\)’s generated by \(V_{I}\)

$$\begin{aligned}{} & {} g_1:(x,y,t,u,v)\rightarrow (x+\epsilon _{1},y,t,u,v),~g_2:(x,y,t,u,v)\rightarrow (x,y+\epsilon _{2},t,u,v),\nonumber \\{} & {} g_3:(x,y,t,u,v)\rightarrow (x,y,t+\epsilon _{3},u,v), ~g_4:(x,y,t,u,v)\rightarrow (x,ye^{-\epsilon _{4}},t,u,ve^{\epsilon _{4}}),\nonumber \\{} & {} g_5:(x,y,t,u,v)\rightarrow (x+\beta t\epsilon _{5},y,t,u-\epsilon _{5},v),\nonumber \\{} & {} g_{6}: (x,y,t,u,v)\rightarrow (xe^{\epsilon _{6}},ye^{-\epsilon _{6}},t^{2\epsilon _{6}},ue^{-\epsilon _{6}},v). \end{aligned}$$
(13)

If \({\bar{f}}(x, y, t)\) and \({\bar{g}}(x, y, t)\) are certain solutions for System (2), the corresponding solutions for System (2) can be obtained

$$\begin{aligned}{} & {} u^{(1)}={\bar{f}}(x-\epsilon _{1},y,t),~v^{(1)}={\bar{g}}(x-\epsilon _{1},y,t),\nonumber \\{} & {} u^{(2)}={\bar{f}}(x,y-\epsilon _{2},t), ~v^{(2)}={\bar{g}}(x,y-\epsilon _{2},t),\nonumber \\{} & {} u^{(3)}={\bar{f}}(x,y,t-\epsilon _{3}),~v^{(3)}={\bar{g}}(x,y,t-\epsilon _{3}),\nonumber \\{} & {} u^{(4)}={\bar{f}}(x,ye^{\epsilon {4}},t),~v^{(4)}=e^{\epsilon _{4}}{\bar{g}}(x,ye^{\epsilon _{4}},t),\nonumber \\{} & {} u^{(5)}={\bar{f}}(x-\beta t\epsilon _{5},y,t)-\epsilon _{5},~v^{(5)}={\bar{g}}(x-\beta t\epsilon _{5},y,t),\nonumber \\{} & {} u^{(6)}=e^{-\epsilon _{6}}{\bar{f}}(xe^{-\epsilon _{6}},ye^{\epsilon _{6}},te^{-2\epsilon _{6}}), ~v^{(6)}={\bar{g}}(xe^{-\epsilon _{6}},ye^{\epsilon _{6}},te^{-2\epsilon _{6}}). \end{aligned}$$
(14)

2.3 Optimal System for System (2)

According to the methods in Ref. [50, 70], we construct an optimal system of one-dimensional subalgebras for System (2) in this section.

Lie algebra for System (2) spanned via Lie Point Symmetry Generators (10) can be written as

$$\begin{aligned} {\widetilde{V}}=q_{1}V_{1}+q_{2}V_{2}+q_{3}V_{3}+q_{4}V_{4}+q_{5}V_{5}+q_{6}V_{6}, \end{aligned}$$
(15)

where \(q_{1},q_{2},\ldots ,q_{6}\) are the real constants. Linear transformations of the vector \(q=(q_{1},q_{2},\ldots ,q_{6})\) are found from their generator

$$\begin{aligned} E_{\imath }=\sum _{\jmath =1}^{6}c_{\imath \jmath }^{\lambda }q_{\jmath }\frac{\partial }{\partial q_{\lambda }},(\lambda =1,2,\ldots ,6), \end{aligned}$$
(16)

where \(c_{\imath \jmath }^{\lambda }\) are the structure constants of the commutation table.

According to Expressions (16) and Table 1, \(E_{1}, E_{2},~E_{3},~E_{4},~E_{5}\) and \(E_{6}\) can be written as

$$\begin{aligned}{} & {} E_{1}=q_{6}\frac{\partial }{\partial q_{1}},~E_{2}=\beta q_{5}\frac{\partial }{\partial q_{1}}+2q_{6}\frac{\partial }{\partial q_{2}},~E_{3}=-(q_{4}+q_{6})\frac{\partial }{\partial q_{3}},\nonumber \\{} & {} E_{4}=q_{3}\frac{\partial }{\partial q_{3}},~E_{5}=-\beta q_{2}\frac{\partial }{\partial q_{1}}-q_{6}\frac{\partial }{\partial q_{5}},\nonumber \\{} & {} E_{6}=-q_{1}\frac{\partial }{\partial q_{1}}-2q_{2}\frac{\partial }{\partial q_{2}}+q_{3}\frac{\partial }{\partial q_{3}}+q_{5}\frac{\partial }{\partial q_{5}}. \end{aligned}$$
(17)

For \(E_{1}, E_{2},~E_{3},~E_{4},~E_{5}\) and \(E_{6}\), the Lie equations with parameters \(b_{\imath }\) and the initial condition \({\widetilde{q}}|_{b_{\imath }=0}=q\) can be written as

$$\begin{aligned}{} & {} \frac{\partial {\widetilde{q}}_{1}}{\partial b_{1}}={\widetilde{q}}_{6},~\frac{\partial {\widetilde{q}}_{2}}{\partial b_{1}}=0,~\frac{\partial {\widetilde{q}}_{3}}{\partial b_{1}}=0,~\frac{\partial {\widetilde{q}}_{4}}{\partial b_{1}}=0,~\frac{\partial {\widetilde{q}}_{5}}{\partial b_{1}}=0,~\frac{\partial {\widetilde{q}}_{6}}{\partial b_{1}}=0,\nonumber \\{} & {} \frac{\partial {\widetilde{q}}_{1}}{\partial b_{2}}=\beta {\widetilde{q}}_{5},~\frac{\partial {\widetilde{q}}_{2}}{\partial b_{2}}=2{\widetilde{q}}_{6},~\frac{\partial {\widetilde{q}}_{3}}{\partial b_{2}}=0,~\frac{\partial {\widetilde{q}}_{4}}{\partial b_{2}}=0,~\frac{\partial {\widetilde{q}}_{5}}{\partial b_{2}}=0,~\frac{\partial {\widetilde{q}}_{6}}{\partial b_{2}}=0,\nonumber \\{} & {} \frac{\partial {\widetilde{q}}_{1}}{\partial b_{3}}=0,~\frac{\partial {\widetilde{q}}_{2}}{\partial b_{3}}=0,~\frac{\partial {\widetilde{q}}_{3}}{\partial b_{3}}=-({\widetilde{q}}_{4}+{\widetilde{q}}_{6}),~\frac{\partial {\widetilde{q}}_{4}}{\partial b_{3}}={\widetilde{q}}_{3},~\frac{\partial {\widetilde{q}}_{5}}{\partial b_{3}}=0,~\frac{\partial {\widetilde{q}}_{6}}{\partial b_{3}}=0,\nonumber \\{} & {} \frac{\partial {\widetilde{q}}_{1}}{\partial b_{4}}=0,~\frac{\partial {\widetilde{q}}_{2}}{\partial b_{4}}=0,~\frac{\partial {\widetilde{q}}_{3}}{\partial b_{4}}={\widetilde{q}}_{3},~\frac{\partial {\widetilde{q}}_{4}}{\partial b_{4}}=0,~\frac{\partial {\widetilde{q}}_{5}}{\partial b_{4}}=0,~\frac{\partial {\widetilde{q}}_{6}}{\partial b_{4}}=0,\nonumber \\{} & {} \frac{\partial {\widetilde{q}}_{1}}{\partial b_{5}}=-\beta {\widetilde{q}}_{2},~\frac{\partial {\widetilde{q}}_{2}}{\partial b_{5}}=0,~\frac{\partial {\widetilde{q}}_{3}}{\partial b_{5}}=0,~\frac{\partial {\widetilde{q}}_{4}}{\partial b_{5}}=0,~\frac{\partial {\widetilde{q}}_{5}}{\partial b_{5}}=-{\widetilde{q}}_{6},~\frac{\partial {\widetilde{q}}_{6}}{\partial b_{5}}=0,\nonumber \\{} & {} \frac{\partial {\widetilde{q}}_{1}}{\partial b_{6}}=-{\widetilde{q}}_{1},~\frac{\partial {\widetilde{q}}_{2}}{\partial b_{6}}=-2{\widetilde{q}}_{2},~\frac{\partial {\widetilde{q}}_{3}}{\partial b_{6}}={\widetilde{q}}_{3},~\frac{\partial {\widetilde{q}}_{4}}{\partial b_{6}}=0,~\frac{\partial {\widetilde{q}}_{5}}{\partial b_{6}}={\widetilde{q}}_{5},~\frac{\partial {\widetilde{q}}_{6}}{\partial b_{6}}=0. \end{aligned}$$
(18)

Solutions to Eqs. (18) give the transformation

$$\begin{aligned}{} & {} T_{1}:~{\widetilde{q}}_{1}=q_{1}+b_{1}q_{6},~{\widetilde{q}}_{2}=q_{2},~{\widetilde{q}}_{3}=q_{3}, ~{\widetilde{q}}_{4}=q_{4},~{\widetilde{q}}_{5}=q_{5},~{\widetilde{q}}_{6}=q_{6},\nonumber \\{} & {} T_{2}:~{\widetilde{q}}_{1}=q_{1}+\beta b_{2}q_{5},~{\widetilde{q}}_{2}=q_{2}+2b_{2}q_{6},~{\widetilde{q}}_{3}=q_{3},~{\widetilde{q}}_{4}=q_{4}, ~{\widetilde{q}}_{5}=q_{5},~{\widetilde{q}}_{6}=q_{6},\nonumber \\{} & {} T_{3}:~{\widetilde{q}}_{1}=q_{1},~{\widetilde{q}}_{2}=q_{2},~{\widetilde{q}}_{3}=q_{3}-b_{3}(q_{4}+q_{6}), ~{\widetilde{q}}_{4}=q_{4},~\widetilde{q_{5}}=q_{5},~\widetilde{q_{6}}=q_{6},\nonumber \\{} & {} T_{4}:~\widetilde{q_{1}}=q_{1},~{\widetilde{q}}_{2}=q_{2},~{\widetilde{q}}_{3}=q_{3}e^{b_{4}}, ~{\widetilde{q}}_{4}=q_{4},~\widetilde{q_{5}}=q_{5},~{\widetilde{q}}_{6}=q_{6},\nonumber \\{} & {} T_{5}:~\widetilde{q_{1}}=q_{1}-\beta b_{5}q_{2},~{\widetilde{q}}_{2}=q_{2},~{\widetilde{q}}_{3}=q_{3},~{\widetilde{q}}_{4}=q_{4}, ~{\widetilde{q}}_{5}=q_{5}-b_{5}q_{6},~{\widetilde{q}}_{6}=q_{6},\nonumber \\{} & {} T_{6}:~{\widetilde{q}}_{1}=q_{1}e^{-b_{6}},~{\widetilde{q}}_{2}=q_{2}e^{-2b_{6}},~{\widetilde{q}}_{3}=q_{3}e^{b_{6}}, ~{\widetilde{q}}_{4}=q_{4},~{\widetilde{q}}_{5}=q_{5}e^{b_{6}},~{\widetilde{q}}_{6}=q_{6}.\nonumber \\ \end{aligned}$$
(19)

Motivated by Ref. [71], we construct an optimal system of one-dimensional subalgebras for System (2) through the simplifications of the vector

$$\begin{aligned} q=(q_{1},q_{2},q_{3},q_{4},q_{5},q_{6}), \end{aligned}$$
(20)

with the transformations \(T_{1}-T_{6}\). As a result, we will find the simplest representatives of each class of similar Vector (20). Substituting these representatives in Expression (15), we will obtain the optimal system of one-dimensional subalgebras of System (2).

  • Case 1 \(q_{6}\ne 0\) Taking \(b_{1}=-\frac{q_{1}}{q_{6}}\) in \(T_{1}\), \(b_{2}=-\frac{q_{2}}{2q_{6}}\) in \(T_{2}\) and \(b_{5}=\frac{q_{5}}{q_{6}}\) in \(T_{5}\), we can obtain \(q_{1}=q_{2}=q_{5}=0\). Thus, Vector (20) is reduced to the form

    $$\begin{aligned} (0,0,q_{3},q_{4},0,q_{6}),~q_{6}\ne 0. \end{aligned}$$
    (21)

    If we take \(q_{4}\ne 0\) from Vector (21) and subject it to the transformations \(T_{3}\) with \(b_{3}=\frac{q_{3}}{q_{4}+q_{6}}\), we obtain

    $$\begin{aligned} (0,0,0,q_{4},0,q_{6}),~q_{6}\ne 0,~q_{4}\ne 0. \end{aligned}$$
    (22)

    Thus, the following representatives for the optimal system can be obtained,

    $$\begin{aligned} V_{6}\pm V_{4}. \end{aligned}$$
    (23)

    We next take \(q_{4}=0\) which gives the reduced vector

    $$\begin{aligned} (0,0,q_{3},0,0,q_{6}),~q_{6}\ne 0. \end{aligned}$$
    (24)

    Thus, taking all possible combinations, we obtain the representations

    $$\begin{aligned} V_{6},~V_{6}\pm V_{3}. \end{aligned}$$
    (25)

  • Case 2 \(q_{6}=0\) This will be divided into the following subcases. 2.1. \(q_{5}\ne 0\) Taking \(b_2=-\frac{q_{1}}{\beta q_{5}}\) in \(T_2\), we can obtain \(q_1=0\). Thus, Vector (20) is reduced to the form

    $$\begin{aligned} (0,q_{2},q_{3},q_{4},q_{5},0),~q_{5}\ne 0. \end{aligned}$$
    (26)

    If we take \(q_{4}\ne 0\) from the reduced vector (26) and subject it to the transformations \(T_{3}\) with \(b_{3}=\frac{q_{3}}{q_{4}}\), we obtain

    $$\begin{aligned} (0,q_{2},0,q_{4},q_{5},0),~q_{5}\ne 0,~q_{4}\ne 0. \end{aligned}$$
    (27)

    Thus, the following representatives for the optimal system can be obtained,

    $$\begin{aligned} V_{5}\pm V_{4},~V_{5}\pm V_{4}\pm V_{2}. \end{aligned}$$
    (28)

    We next take \(q_{4}=0\) which gives the reduced vector

    $$\begin{aligned} (0,q_{2},q_{3},0,q_{5},0),~q_{5}\ne 0. \end{aligned}$$
    (29)

    Thus, taking all possible combinations, we obtain

    $$\begin{aligned} V_{5},~V_{5}\pm V_{2},~V_{5}\pm V_{3},~V_{5}\pm V_{3}\pm V_{2}. \end{aligned}$$
    (30)

    2.2. \(q_{5}=0\) Taking \(b_5=\frac{q_{1}}{\beta q_{2}}\) in \(T_5\), we can obtain \(q_1=0\). Thus, Vector (20) is reduced to the form

    $$\begin{aligned} (0,q_{2},q_{3},q_{4},0,0),~q_{2}\ne 0. \end{aligned}$$
    (31)

    Similarly, we get

    $$\begin{aligned} V_{2},~V_{2}\pm V_{4},~V_{2}\pm V_{3}. \end{aligned}$$
    (32)

    2.2.1. \(q_{2}=0\) Taking \(b_3=\frac{q_{3}}{\beta q_{4}}\) in \(T_3\), we can obtain \(q_3=0\). Thus, Vector (20) is reduced to the form

    $$\begin{aligned} (q_{1},0,0,q_{4},0,0),~q_{4}\ne 0. \end{aligned}$$
    (33)

    Thus, taking all possible combinations, we obtain

    $$\begin{aligned} V_{4},~V_{4}\pm V_{1}. \end{aligned}$$
    (34)

    2.2.1.1. \(q_{4}=0\) Vector (20) is reduced to the form

    $$\begin{aligned} (q_{1},0,q_{3},0,0,0). \end{aligned}$$
    (35)

    Thus, taking all possible combinations, we obtain

    $$\begin{aligned} V_{1},~V_{3},~V_{1}\pm V_{3}. \end{aligned}$$
    (36)

    Consequently, the optimal system of the one-dimensional subalgebras for System (2) given via Lie Point Symmetry Generators (10) is the following form:

    $$\begin{aligned}{} & {} V_{1},~V_{2},~V_{3},~V_{4},~V_{5},~V_{6},~V_{1}\pm V_{3},~V_{4}\pm V_{1},~V_{2}\pm V_{3},~V_{2}\pm V_{4},~V_{5}\pm V_{2},\nonumber \\{} & {} V_{5}\pm V_{3},~V_{5}\pm V_{4},~V_{5}\pm V_{4}\pm V_{2},~V_{5}\pm V_{3}\pm V_{2},~V_{6}\pm V_{4},~V_{6}\pm V_{3}. \end{aligned}$$
    (37)

3 Symmetry Reductions and Analytic Solutions for System (2)

In this section, we get the reduction equations for System (2) via Optimal System (37). Certain solutions for System (2) can be constructed via the reduction equations.

  • Case 1 For the Lie point symmetry \(V_2=\partial _t\), the following group-invariant solutions can be obtained:

    $$\begin{aligned} u=P(x_1,y_1),~v=Q(x_1,y_1), \end{aligned}$$
    (38)

    where \(x_1=x\), \(y_1=y\), P and Q denote the functions of \(x_1\) and \(y_1\). Substituting Expressions (38) into System (2), the reduced system can be obtained:

    $$\begin{aligned} \begin{aligned}&\alpha P_{x_{1}x_{1}y_{1}}-2\alpha Q_{x_{1}x_{1}}-\beta P_{x_{1}}P_{y_{1}}-\beta P P_{x_{1}y_{1}}=0,\\&\alpha Q_{x_{1}x_{1}}+\beta P_{x_{1}}Q+\beta Q_{x_{1}}P=0. \end{aligned} \end{aligned}$$
    (39)

Using the Lie group method to System (39), we have

$$\begin{aligned} \xi _1=s_{1}x_{1}+s_{3},~\eta _1=-(s_{1}+s_{2})y_{1},~\phi _{1}=-s_{1}P,~\varphi _{1}=s_{2}Q, \end{aligned}$$
(40)

where \(s_1\), \(s_2\) and \(s_3\) are the real constants. Lie point symmetry generators for System (39) are derived as follows:

$$\begin{aligned}{} & {} \Gamma _1=\frac{\partial }{\partial x_1},~\Gamma _2=\frac{\partial }{\partial y_1},~\Gamma _3=-y_{1}\frac{\partial }{\partial y_1}+Q\frac{\partial }{\partial Q},\nonumber \\{} & {} \Gamma _4=x_{1}\frac{\partial }{\partial x_1}-y_1\frac{\partial }{\partial y_1}-P\frac{\partial }{\partial P}. \end{aligned}$$
(41)

For the Lie point symmetry \(n_{1}\Gamma _1+\Gamma _2\), the symmetry produces the following group-invariant solutions:

$$\begin{aligned} f=x_{1}-n_{1}y_{1},~P=H(f),~Q=K(f), \end{aligned}$$
(42)

where \(n_{1}\) is a real constant, H and K are the real functions of f. Substituting Expressions (42) into System (39) gives rise to the following reduced equations:

$$\begin{aligned} \begin{aligned}&-n_{1}\alpha H_{fff}-2\alpha K_{ff}+n_{1}\beta HH_{ff}+n_{1}\beta H_{f}^2=0,\\&\alpha K_{ff}+\beta HK_{f}+\beta KH_{f}=0. \end{aligned} \end{aligned}$$
(43)

Based on the \(\left( \frac{G^{'}}{G}\right) \) expansion method [72], we suppose solutions for System (43) have the following forms:

$$\begin{aligned} H=\sum _{j=0}^{m}a_j\left( \frac{G^{'}}{G}\right) ^{j}, ~K=\sum _{j=0}^{n}b_j\left( \frac{G^{'}}{G}\right) ^{j}, \end{aligned}$$
(44)

where m and n are the positive integers, \(a_{j}\)’s and \(b_{j}\)’s are the real constants, and G is a function of f. G satisfies the following ordinary differential equation

$$\begin{aligned} G^{''}+BG^{'}+AG=0, \end{aligned}$$
(45)

where \(G^{'}=\frac{\text {d}G}{\text {d}f}\) and \(G^{''}=\frac{\text {d}^2G}{\text {d}f^2}\), A and B are the real constants. m and n can be determined via the homogeneous balance method between the highest order derivative term and the nonlinear term appearing in System (43). Thus, we derive \(m=1\) and \(n=2\). Substituting Expressions (44) and Constraint (45) into System (43) as well as setting the coefficients of the like powers \((\frac{G^{'}}{G})\) equal to vanish, we have

$$\begin{aligned} a_{0}=\frac{B\alpha }{\beta },~a_{1}=\frac{2\alpha }{\beta },~b_{0}=\frac{2n_{1}\alpha A}{\beta },~b_{1}=\frac{2\alpha n_{1}B}{\beta },~b_{2}=\frac{2\alpha n_{1}}{\beta }. \end{aligned}$$
(46)

When \(B^2-4A>0\), hyperbolic-function solutions for System (2) can be derived

$$\begin{aligned} \begin{aligned}&u(x,y,t)\\&\quad {=}\frac{B\alpha }{\beta }{+}\frac{2\alpha }{\beta } \left\{ \frac{\sqrt{B^2-4A}}{2}\frac{ C_{1}\sinh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] {+}C_{2}\cosh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] }{C_{1}\cosh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] {+}C_{2}\sinh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] } {-}\frac{B}{2}\right\} ,\\&v(x,y,t)\\&\quad {=}\frac{2\alpha n_{1}B}{\beta }\left\{ \frac{\sqrt{B^2-4A}}{2}\frac{ C_{1}\sinh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] {+}C_{2}\cosh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] }{C_{1}\cosh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] {+}C_{2}\sinh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] }-\frac{B}{2}\right\} \\&\qquad +\frac{2\alpha n_{1}}{\beta }\left\{ \frac{\sqrt{B^2-4A}}{2}\frac{ C_{1}\sinh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] {+}C_{2}\cosh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] }{C_{1}\cosh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] {+}C_{2}\sinh \left[ \frac{\sqrt{B^2-4A}}{2}(x-n_{1}y)\right] }-\frac{B}{2}\right\} ^2\\&\qquad +\frac{2n_{1}\alpha A}{\beta }, \end{aligned}\nonumber \\ \end{aligned}$$
(47)

where \(C_1\) and \(C_2\) are the real constants.

When \(B^2-4A=0\), solutions for System (2) can be obtained

$$\begin{aligned} \begin{aligned} u(x,y,t)&=\frac{B\alpha }{\beta }+\frac{2\alpha }{\beta }\left[ \frac{C_{4}}{C_{3}+C_{4}(x-n_{1}y)}-\frac{B}{2}\right] ,\\ v(x,y,t)&=\frac{2n_{1}\alpha A}{\beta }+\frac{2\alpha n_{1}B}{\beta }\left[ \frac{C_{4}}{C_{3}+C_{4}(x-n_{1}y)}-\frac{B}{2}\right] \\&\quad +\frac{2\alpha n_{1}}{\beta }\left[ \frac{C_{4}}{C_{3}+C_{4}(x-n_{1}y)}-\frac{B}{2}\right] ^2, \end{aligned} \end{aligned}$$
(48)

where \(C_3\) and \(C_4\) are the real constants.

When \(B^2-4A<0\), we get trigonometric-function solutions for System (2)

$$\begin{aligned} \begin{aligned}&u(x,y,t)\\&\quad {=}\frac{B\alpha }{\beta }{+}\frac{2\alpha }{\beta }\left\{ \frac{\sqrt{4A-B^2}}{2}\frac{C_{6}\text {cos}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] {-}C_{5}\text {sin}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] }{C_{5}\text {cos}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] {+}C_{6}\text {sin}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] } {-}\frac{B}{2}\right\} ,\\&v(x,y,t)\\&\quad {=}\frac{2n_{1}\alpha A}{\beta }{+}\frac{2\alpha n_{1}B}{\beta }\left\{ \frac{\sqrt{4A{-}B^2}}{2}\frac{C_{6}\text {cos}\left[ \frac{\sqrt{4A{-}B^2}}{2}(x{-}n_{1}y)\right] {-}C_{5}\text {sin}\left[ \frac{\sqrt{4A{-}B^2}}{2}(x{-}n_{1}y)\right] }{C_{5}\text {cos}\left[ \frac{\sqrt{4A{-}B^2}}{2}(x{-}n_{1}y)\right] {+}C_{6}\text {sin}\left[ \frac{\sqrt{4A{-}B^2}}{2}(x{-}n_{1}y)\right] } {-}\frac{B}{2}\right\} \\&\qquad {+}\frac{2\alpha n_{1}}{\beta }\left\{ \frac{\sqrt{4A-B^2}}{2}\frac{C_{6}\text {cos}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] {-}C_{5}\text {sin}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] }{C_{5}\text {cos}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] {+}C_{6}\text {sin}\left[ \frac{\sqrt{4A-B^2}}{2}(x-n_{1}y)\right] }-\frac{B}{2}\right\} ^2, \end{aligned}\nonumber \\ \end{aligned}$$
(49)

where \(C_5\) and \(C_6\) are the real constants.

  • Case 2 For the Lie point symmetry \(V^{(1)}=V_3+V_1\), we derive the following group-invariant solutions:

    $$\begin{aligned} f_1=x-y~,h_1=t,~u=R(f_1,h_1),~v=S(f_{1},h_{1}), \end{aligned}$$
    (50)

    where R and S denote the functions of \(f_1\) and \(h_1\). Substituting Expressions (50) into System (2), the reduced system can be derived as

    $$\begin{aligned} \begin{aligned}&-R_{h_{1}f_{1}}-\alpha R_{f_{1}f_{1}f_{1}}-2\alpha S_{f_{1}f_{1}} +\beta RR_{f_{1}f_{1}}+\beta R_{f_{1}}^{2}=0,\\&-S_{h_{1}}-\alpha S_{f_{1}f_{1}}-\beta RS_{f_{1}}-\beta R_{f_{1}}S=0. \end{aligned} \end{aligned}$$
    (51)

Applying the Lie group method on System (51), we have

$$\begin{aligned} \begin{aligned} \xi _2=s_{4}f_{1}+s_{5},~\eta _2=2s_{4}h_{1}+s_{6}, ~\phi _{2}=-s_{4}R,~\varphi _{2}=-2s_{4}S, \end{aligned} \end{aligned}$$
(52)

where \(s_4\), \(s_5\) and \(s_6\) are the real constants. Thus, the Lie point symmetry generators for Eqs. (51) can be derived as follows:

$$\begin{aligned} \begin{aligned} \Upsilon _1=&\frac{\partial }{\partial f_1},~\Upsilon _2=\frac{\partial }{\partial h_1},~\Upsilon _3=f_{1}\frac{\partial }{\partial f_{1}}+2h_{1}\frac{\partial }{\partial h_{1}}-2S\frac{\partial }{\partial S}-R\frac{\partial }{\partial R}. \end{aligned} \end{aligned}$$
(53)

For the Lie point symmetry \(k_1\Upsilon _1+\Upsilon _2\), the symmetry produces the following group-invariant solutions:

$$\begin{aligned} z=f_1-k_1h_1,~R=\psi (z),~S=\chi (z), \end{aligned}$$
(54)

where \(k_1\) is a real constants, and \(\psi \) and \(\chi \) are the real functions of z. Substituting Expressions (54) into System (51), we get the following reduced equations:

$$\begin{aligned} \begin{aligned}&k_{1}\psi _{zz}-\alpha \psi _{zzz}-2\alpha \chi _{zz}+\beta \psi \psi _{zz}+\beta \psi _{z}^2=0,\\&k_{1}\chi _{z}+\alpha \chi _{zz}+\beta \psi \chi _{z}+\beta \psi _{z}\chi =0. \end{aligned} \end{aligned}$$
(55)

Based on the polynomial expansion method [73], we suppose solutions for Eqs. (55) have the following forms:

$$\begin{aligned} \psi =\sum _{\iota =-M}^{M}d_{\iota } W(z)^{\iota },~\chi =\sum _{\kappa =-N}^{N}g_{\kappa } W(z)^{\kappa }, \end{aligned}$$
(56)

where M and N are the positive integers, \(b_{\iota }\)’s and \(g_{\kappa }\)’s are the real constants. Here, W satisfies

$$\begin{aligned} \frac{dW}{dz}=W^{2}(z)+p_1z+p_2, \end{aligned}$$
(57)

where \(p_1\) is a real constant and \(p_2\) is a non-negative real constant. M and N can be determined via the homogeneous balance method. We derive \(M=1\) and \(N=2\). Substituting Expressions (56) and Constraint (57) into System (55) as well as setting the coefficients of W(z) equal to zero, we obtain the following results:

$$\begin{aligned}{} & {} d_{0}=-\frac{k_{1}}{\beta },~d_{1}=-\frac{2\alpha }{\beta },~g_{0}=\frac{2\alpha p_{2}}{\beta },\nonumber \\{} & {} g_{2}=\frac{2\alpha }{\beta },~d_{-1}=g_{-2}=g_{-1}=g_{1}=0. \end{aligned}$$
(58)

We derive trigonometric-function solutions of System (2) as

$$\begin{aligned} u(x,y,t)= & {} -\frac{k_{1}}{\beta }-\frac{2\alpha \sqrt{p_{2}}}{\beta }\text {tan}[\sqrt{p_{2}}(c+x-y-k_{1}t)],\nonumber \\ v(x,y,t)= & {} \frac{2\alpha p_{2}\text {tan}[\sqrt{p_{2}}(c+x-y-k_{1}t)]^2}{\beta }+\frac{2p_{2}\alpha }{\beta }. \end{aligned}$$
(59)

  • Case 3 For the Lie point symmetry \(V^{(2)}= V_2+V_3\), the following group-invariant solutions can be obtained:

    $$\begin{aligned} f_2=x,~h_2=y-t,u=\mu (f_2,h_2),~v=\nu (f_{2},h_{2}), \end{aligned}$$
    (60)

    where \(\mu \) and \(\nu \) are the functions of \(f_2\) and \(h_2\).

Substituting Expressions (60) into System (2), we have the following reduced equations:

$$\begin{aligned} \begin{aligned}&\mu _{h_{2}h_{2}}-\alpha \mu _{h_{2}f_{2}f_{2}}+2\alpha \nu _{f_{2}f_{2}}+\beta \mu \mu _{h_{2}f_{2}}+\beta \mu _{f_{2}}\mu _{h_{2}}=0,\\&\nu _{h_{2}}+\alpha \nu _{f_{2}f_{2}}+\beta \mu _{f_{2}}\nu +\mu \nu _{f_{2}}=0. \end{aligned} \end{aligned}$$
(61)

Using Lie group method to System (61), we obtain

$$\begin{aligned} \begin{aligned}&\xi _3=s_{7}f_{2}+s_{8},~\eta _3=2s_{7}h_{2}+s_{9}, ~\phi _{3}=-s_{7}\mu ,~\psi _{3}=-3s_{7}\nu , \end{aligned} \end{aligned}$$
(62)

where \(s_7\), \(s_{8}\) and \(s_{9}\) are the real constants. Thus, the Lie point symmetry generators for System (61) are derived as follows:

$$\begin{aligned} \begin{aligned} \Theta _1=&\frac{\partial }{\partial f_2},~\Theta _2=\frac{\partial }{\partial h_2},~\Theta _3=f_{2}\frac{\partial }{\partial f_2}+2h_{2}\frac{\partial }{\partial h_{2}}-\mu \frac{\partial }{\partial \mu }-3\nu \frac{\partial }{\partial \nu }. \end{aligned} \end{aligned}$$
(63)

For the Lie point symmetry \(k_{2}\Theta _1 +\Theta _2\), the symmetry produces the following group-invariant solutions:

$$\begin{aligned} z_{1}=f_2-k_2h_2,~L=\mu (z_1),~K=\nu (z_{1}), \end{aligned}$$
(64)
Fig. 1
figure 1

One soliton via Solutions (70) with the parameters as \(\alpha = 1\), \(\beta = 1\), \(k_{2} = 2\)

Full size image

where \(k_{2}\) is a real constant, L and K are the real functions of \(z_1\). Substituting Expressions (64) into System (61), we have the following reduced equations:

$$\begin{aligned} \begin{aligned}&k_{2}^2L_{z_1}+\alpha k_{2}L_{z_1z_1z_1}+2\alpha K_{z_1z_1}-\beta k_{2}LL_{z_1}-\beta k_{2}L_{z_1}^2=0,\\&k_{2}K_{z_1}-\alpha K_{z_1z_1}-\beta K_{z_1}L-\beta KL_{z_1}=0. \end{aligned} \end{aligned}$$
(65)

Based on the Riccati equation expansion method [74], the solutions for System (65) have the following forms:

$$\begin{aligned} L=\sum _{\gamma =-e}^{e}\theta _{\gamma } \omega (z_{1})^{\gamma },~ K=\sum _{\delta =-q}^{q}\rho _{\delta } \omega (z_{1})^{\delta }, \end{aligned}$$
(66)

where \(\omega (z_{1})\) satisfy the Riccati equation

$$\begin{aligned} \omega _{z_{1}}=1-\omega ^{2}(z_{1}), \end{aligned}$$
(67)

with

$$\begin{aligned} \omega (z_{1})=\tanh (z_{1}), \end{aligned}$$
(68)

where \(\theta _{\gamma }\)’s and \(\rho _{\delta }\)’s are the real constants, e and q are the integers that can be determined via the homogeneous balance method. We derive \(e=1\) and \(q=2\). Substituting Expressions (66) into Eqs. (65) with Constraints (67) and (68), and setting the coefficients of \(\omega (z_{1})\) equal to vanish, we obtain the following results:

$$\begin{aligned}{} & {} \theta _{0}=\frac{k_{2}}{\beta },~\theta _{1}=\frac{2\alpha }{\beta }, ~\rho _{0}=-\frac{2k_{2}\alpha }{\beta }, \rho _{2}=\frac{2k_{2}\alpha }{\beta },\nonumber \\{} & {} \theta _{-1}=\rho _{-2}=\rho _{-1}=\rho _{1}=0. \end{aligned}$$
(69)

We derive the soliton solutions of System (2) as

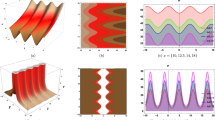
$$\begin{aligned}{} & {} u(x,y,t)=\frac{k_{2}}{\beta }+\frac{2\alpha }{\beta }\tanh {[x-k_{2}(y-t)]},\nonumber \\{} & {} v(x,y,t)= -\frac{2k_{2}\alpha }{\beta }\ +\frac{2k_{2}\alpha }{\beta }\tanh ^{2}{[x-k_{2}(y-t)]}. \end{aligned}$$
(70)

Figures 1 exhibit the propagation of one soliton. One kink-soliton on the (x, y) planes propagate along the same direction in y-axis, as seen in Fig. 1\((a_{1})\)–\((a_{3})\); One bell-soliton on the (x, y) planes propagate along the same direction in y-axis, as shown in Fig. 1\((b_{1})\)–\((b_{3})\).

4 Conclusions

Shallow water waves have been referred to the waves with the bottom boundary affecting the movement of water quality points when the ratio of water depth to wavelength is small. In this paper, a (2+1)-dimensional generalized modified dispersive water-wave system in fluid mechanics, i.e., System (2), has been investigated. We have derived Lie Point Symmetry Generators (10) and Lie Symmetry Groups (13) for System (2) via the Lie group method. Optimal system of the one-dimensional subalgebras for System (2) has been given as Lie Symmetry Generators (10). Symmetry Reductions (43), (55) and (65) for System (2) have been derived from Cases 1–3. Hyperbolic Function Solutions (47), Rational Solutions (48), Trigonometric Function Solutions (49) and (59), and Soliton Solutions (70) for System (2) have been obtained via the polynomial expansion, Riccati equation expansion and \(\left( \frac{G^{'}}{G}\right) \) expansion methods. In addition, these hyperbolic function, rational and trigonometric function solutions will help to study the analytical solutions of other nonlinear evolution equations in fluid mechanics, plasma physics, nonlinear dynamics, nonlinear optics and mathematical physics. In the future, we will try to construct the soliton, breather, rouge-wave and hybrid solutions via the Darboux transformation and bilinear neural network method.