Calibration of kinematic hardening parameters on sheet metal with a Computer Numerical Control machine

Abstract

This article investigates the relevance, for material parameter identification, of substituting a set of 3 experiments (uniaxial tension, monotonous shear and reverse shear tests) by a test performed by a Computer Numerical Control (CNC) machine, where a spherical tool replacing the cutting tool performs a simple path on a fixed square sheet. This tool path is defined by one indent, one go linear path, one further indent and one return linear path. This so called line test is a simple version of Single Point Incremental Forming (SPIF) process where the depth of the produced part is however usually smaller. Completed by a uniaxial tensile test, this line test allows identifying the parameters of both kinematic and isotropic hardening models. This CNC test provides an easy alternative to tensile-compression test or reverse shear test. It generates non uniform cyclic loadings in sheets which are necessary to accurately identify kinematic hardening laws. This identification method of isotropic and kinematic hardening is applied on a brass CuZn37 sheet of 1 mm thick. It uses only the experimental measured force during the line test and a classical tensile test. The Levenberg–Marquardt algorithm is used to determine the optimal hardening material set of parameters, through inverse modelling based on finite element (FE) simulations. The sensitivity of the identification method is evaluated and the approach is validated by the capacity of the identified hardening material data set to simulate an experimental reverse shear test and a second “SPIF like test” having a more complex shape.

Introduction

None reliable simulation of a manufacturing process can be performed without correct material parameters. The identification of accurate data sets of hardening material laws for metal sheets in the whole range of their plastic field is a real challenge. It usually requires different types of tests (uniaxial tensile, large tensile, monotonous and reverse shear tests) [1], or an optimised shape coupled with Digital Image Correlation (DIC) capturing complex strain field [2, 3]. The material characterization based on a low number of experimental tests (typically one or two tests) or without the use of a DIC system would be an interesting approach for scientists and industries dealing with forming simulations and manufacturing processes.

Indeed uniaxial tensile tests, available in many laboratories and industries, can be used to identify the isotropic hardening parameters but this single tensile test does not solve the issue of identifying kinematic hardening. The present work describes how replacing the reverse shear tests often used to characterize cyclic sheet material behaviour by a test performed by a CNC machine.

To apply reverse loading for the identification of kinematic hardening, cyclic tests of tension–compression type are possible but not straightforward for metal sheets as presented by the comb grip approach proposed by Kuwabara [4]. Reverse shear tests with different pre-strain levels are an interesting alternative but they also required specific equipment [5]. The SPIF process offers a third alternative. The process efficiency in term of parameter identification by inverse modelling has already been demonstrated for pyramid and cones from small pieces of 34 × 34 mm² [6, 7]. Indeed as a SPIF piece is formed by a series of small successive deformations generated by the contact between a tool and a sheet, it activates kinematic hardening. Note that SPIF process belongs to the broad family of Incremental Sheet Forming (ISF) processes. A synthesis of the basic features of the ISF approach (tool path strategy, forming tool, forming limits) and its different variants (SPIF, two-point incremental forming) is available in [8]. Several review papers present the latest progresses of ISF [9] and of SPIF [10, 11]. The enhancement of the formability is the most remarkable feature of the SPIF variant. Indeed, the material reaches its Rupture Limit Diagram (RLD) avoiding the necking event identified by the Forming Limit Diagram (FLD) [12]. The FLD generally presents a V-shape in the in-plane principal strain space. However, in the SPIF case, the FLD shows a linear shape with a negative slope [13]. So the reached maximum plastic strain is significantly higher than the one accessible in the traditional forming processes as deep drawing for instance [14]. Identifying a hardening model by a SPIF test decreases the risk of wrong extrapolation for large strains and solves the issue of the need of specific equipment for reverse loading in sheet.

When both material parameters and boundary conditions are known, the direct simulation of a sheet forming process becomes a routine work. However, to search a single set of material parameters by an inverse modelling approach based on more than one experiment, remains a challenge [15]. The correct material input data generate numerical predictions that minimize the error (the cost function) between the simulation results and the experiments. Hereafter the well-known Levenberg–Marquardt algorithm developed by Kenneth Levenberg and Donald Marquardt is applied [16]. Other algorithms were used in previous works like the genetic algorithm [17] where 3D DIC and FE simulations have been used to determine the material parameters based on tensile tests for a stainless steel sheet. The identification of elastic properties from surface displacement measurements under flexural loading has also been presented in [18]. In this case again, a combination of the finite element analysis and genetic algorithms was used. An heterogeneous testing procedure for anisotropic behaviour has been developed in [19]. This latter approach is based on out-of-plane deformations and Stereo Image Correlation (SIC). Therein, Levenberg–Marquardt algorithm was used to determine the material parameters. The accuracy of this method has been demonstrated and results show that a single non homogeneous complex test is sufficient to completely identify plastic anisotropy parameters for instance. Yet, predicting the occurrence of failure by SPIF FE simulations remains a challenge [20]. Nevertheless successes can be observed as in [21] with the damage model of Xue [22] that decreases the isotropic hardening by a damage function. Note that two damage models were applied on SPIF simulations in [23]: a micromechanically-based Gurson model and a continuum Lemaitre and Chaboche model. The identification approach was only based on a set of plane tests (tensile tests of smooth or notched bars and shear tests). The models and their data sets were validated by the prediction of the maximum achievable wall angle in truncated cones formed by SPIF. The superiority of the Lemaitre type model was proved in this case however many tests were used for the material parameter identifications.

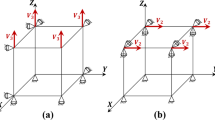
In the present article, the inverse modelling technique based on the Levenberg–Marquardt optimization algorithm is simultaneously applied on only two mechanical tests (SPIF line test and uniaxial tensile test) to identify a single set of material parameters. The line test proposed by [1, 15] offers a simple case of SPIF. The geometry used hereafter to identify brass hardening is described in Fig. 1a. The tool plunges into the material twice. The first step, called ‘Indent test’ gives information about the material out-of-plane behaviour, which is not available within classical plane tests focused on the in-plane behaviour. The second step consists in loading the material in a complex stress state dominated by shear state. This affirmation is confirmed by the low value of triaxiality (mean stress and equivalent stress ratio) in Fig. 1b computed by the simulations presented in "Numerical modelling" section with the final data set identified in "Material identification and validation" section. The fourth step mainly consists in a reverse shear state.

Fig. 1

a Line test experiment, geometry (tool diameter of 10 mm, sheet of 182 × 182 × 1 mm³) and tool steps (step 1, 3: 3 mm; step 2, 4: 100 mm); (b) Triaxiality map at the end of the simulation; (c) Equivalent plastic strain map at the end of the simulation

The focus of this article on kinematic hardening identification and on the line test, covering a moderate strain level (see computed equivalent strain in Fig. 1c defining a maximum strain of 17.2%) brings novelty for the research and industrial communities, as the identification methodology is simple. The line test is shorter and easier than a SPIF cone test and, completed by a single tensile test, it allows the identification of any hardening model for an isotropic sheet.

The current article is organized as follows: "Experiments" section describes the different experiments used to provide the reference data for the chosen application case (brass CuZn37 material). "Numerical modelling" section summarizes the constitutive model and the finite element simulation features. The identification method, its validation and sensitivity are described in "Material identification and validation" section. Some concluding remarks are synthesized in "Conclusions" section while the appendices present additional details on the experiment post processing and on the implemented Levenberg–Marquardt algorithm applied for more than one experiment.

Experiments

Material

Due to its high malleability, low price and excellent corrosion resistance [24], brass is often selected in the plumbing and roof applications, water transport components and standard fittings (tubes, drains, pipes..). Although the application of the single point incremental forming on the brass material is not often studied in the literature, almost the same grade of the brass as used in the current research was investigated in [25, 26]. In this case, the mechanical properties of brass Cu-35Zn were explored with different thicknesses to study the SPIF forming forces. The forming limit diagram was identified by the SPIF process and compared with the one determined by the conventional approach. Also, the effects of the friction during the process and the tool diameter were evaluated. Furthermore, the impact of the tool path strategy on the final mechanical properties of brass 65–35 formed by SPIF was analyzed in [27].

For this study, the brass grade CuZn37 was selected. It is also called yellow brass and composed, according to EN 12,163:2011, by 62% to 64% of copper, 0.1% (max) of lead, 0.1% (max) of iron, 0.3% (max) of nickel and the balance is zinc (≈37%) [28]. It was chosen for this study due to its large fracture strain and high formability (excellent capacity for cold working) [29]. Due to the complex shapes present in plumbing or design furniture, SPIF of brass piece would be an interesting application. A CuZn37 brass sheet of 1.0 mm in thickness has been used. Note that almost no viscous effect is present at room temperature for this brass grade as proved by the experimental campaign of Naka [30] who tested a large range of strain rate (2.2 10^–4 to 2.1 10²).

Hardware equipment and sample geometries

The tensile tests were performed following NBN EN ISO 6892–1 norm with a 100 kN ZWICK ROELL uniaxial tensile machine (Fig. 2a) on samples shown in Fig. 3a. Shear and reverse shear tests were carried out using a bi-axial test machine with a capacity of 100 kN (Fig. 2b) developed at the University of Liège [31, 32]. The two pistons, simultaneously controlled, allow applying bi-axial tests to investigate the yield locus shape. However, in simple shear test, only the horizontal piston generates a displacement, the other piston just prevents any vertical displacement on the horizontal boundaries of the deformed zone (identified by white colour in Fig. 3b).

Fig. 2

a Uniaxial tensile machine; (b) Bi-axial machine; (c) Optical system

Fig. 3

a Geometry of the tensile test sample and (b) the shear test sample (dimensions in mm), shaded zones are within press grips

The monitoring system records and synchronizes the mechanical data (load and displacements) from the two pistons as well as the deformation field measured by the optical system (Fig. 2c). VIC 3D software was used to compute the strain field based on DIC. Shear test is not straightforward to carry out due to the sliding which can occur during the experiment. To decrease this sliding [33], mid-length notches were machined on the samples and a large part of the shear sample is under the grip compared to tensile sample (see sample geometry Fig. 3b).

An old 2.5 axis MIKRON WF1D milling machine (Fig. 4a) was used to carry out the SPIF tests [34]. Two control modes of the tool displacements are available: the Manual Data Input (MDI) mode (Fig. 4b) which allows to manually input the G-code into the machine (dedicated to perform simple geometries) and the Memory mode where the machine receives the G-code from a computer (for more complex geometries). An OMEGA 160 force sensor was used to measure force and torque in the three-dimensional space.

Fig. 4

a Mikron CNC machine; (b) Control system

The line test is already described in the introduction (Fig. 1a). Another test, i.e. the Z shape is presented in Fig. 5. It provides a validation case while the line test is used for identification purpose. Both tests were performed with a 182 mm X 182 mm sheet as illustrated in Figs. 1 and 5. As for the line test, in the Z-shape test, the square metallic sheet is clamped along its edges. 20 bolts prevent any sliding as checked by a black line drawn before the forming process and observed at the test end. The tool plunges into the material twice (step 1 and 3 in Fig. 1 and thick vertical arrows in Fig. 5). The vertical indents are 3 mm and 1.5 mm deep for the first and second indent respectively in the Z shape, half of the line test to keep the same load cell. Indeed the recorded forces for the Z shape are higher due to the forming localisation closer to the edges. The vertical punch forces were measured during each line or Z-shape test and are presented in Figs. 12b and 13 where both force predictions and measurements are compared. Hereafter, Fig. 6 shows the deformed sheets after the removal from the clamping system. Each test was repeated twice and provide a very good reproducibility (both for the measured force and the shape).

Fig. 5

Z-shape test steps (dimensions in mm)

Fig. 6

Final sheet shape after: (a) line test and (b) Z-shape test

The final geometries were measured but were not used in the identification methodology to keep it the as simple as possible, thinking of an easy industrial application.

Result of tensile and shear tests

The tensile stress–strain curve required within the identification process is provided in Fig. 7a. The Simple SHear test (SSH) and Reverse SHear (RSH) also called Bauschinger test are used only as validation for the identified material parameters. The shear stress–strain curves (σ_xy – ε_xyH) are presented in Fig. 7b. Three cyclic shear tests were performed with different pre-strains (ε_xyH = 10%, ε_xyH = 15% and ε_xyH = 25%). The post processing details of force and displacement measurements to reach the stress and strain components shown Fig. 7 can be found in Appendix A.

Fig. 7

a True axial stress-true plastic strain curves for tensile tests in Rolling Direction (RD), Transversal Direction (TD) and Diagonal Direction (DD) at 45° from RD; (b) true shear stress-true shear strain of monotonous and reverse shear tests for 3 pre-strains (ε_xyH = 10%, ε_xyH = 15% and ε_xyH = 25%) with H for Hencky definition of strain.

Bauschinger effect can be observed in Fig. 7b. The yield strength is indeed reduced after the reverse loading, e.g. point A corresponds to a stress of 148 MPa, while it is -109 MPa for point A’. Furthermore, Fig. 7b illustrates the work-hardening stagnation under reverse deformation. This phenomena related to microstructure events requires advanced hardening models as proposed by [35,36,37] to accurately describe the evolution of the back-stress.

For this brass material, the fracture stains in tensile and shear states are relatively close. They correspond to the curve ends in Fig. 7. The maximum true strain is around 40% for the 3 tensile tests while the 2 monotonous shear tests end for a shear strain value of 52%.

Numerical modelling

The FE simulations of the SPIF process as well as of the shear and tensile tests were performed with the home-made finite element code Lagamine developed since the eighties in ULiege [38, 39]. This lagrangian code uses an implicit strategy, handles contact between deformable bodies [40] and has been for a long time applied on deep drawing simulations [41]. Different researchers applied Lagamine for instance on complex characterization tests such as nanoindentation [42] or processes like single point incremental forming [20].

Constitutive law and homogenous stress state simulations

Hereafter, the mechanical behaviour of this brass grade is assumed isotropic due to the close agreement between the tensile stress–strain curves in the three in-plane directions (0°, 45°, 90°) shown in Fig. 7a. An elasto-platic constitutive law was selected as, according to the literature, at room temperature no viscous effect is reported [30]. The elasticity is described by the linear Hooke’s law with an apparent Young’s modulus determined from the uniaxial tensile test: E = 105 GPa. Note that this value is in agreement with [43]. Like in [44], the von Mises criterion was used to model the yield surface. The yield locus size and position follow an isotropic and kinematic hardening assumption. The well-known concept of mixed hardening is described in Fig. 8 reminding that the isotropic hardening can be interpreted as the expansion of the size of the yield surface while the kinematic hardening represents the translation of its centre.

Fig. 8

Yield surface evolution considering mixed hardening

Due to the apparent lack of the saturation of the uniaxial stress–strain curve (Fig. 7a) in the brass material CuZn37, Ludwick’s power law was selected to model the isotropic hardening:

$${\sigma }_{y}={\sigma }_{0}+K{{\varepsilon }_{p}}^{n}$$

(1)

where σ_y and ε_p are respectively the equivalent stress and equivalent plastic strain, σ₀ is the yield stress, K and n are material parameters (n is also called hardening exponent).

For the kinematic hardening, the back-stress X evolution is described by Ziegler law [45]:

$$\dot{\mathbf{X}}={C}_{A}\frac{1}{{\sigma }_{y}}\left({\varvec{\upsigma}}-\mathbf{X}\right).{\dot{\varepsilon }}_{p}-{G}_{A} \mathbf{X} {\dot{\varepsilon }}_{p}$$

(2)

where C_A and G_A are the initial kinematic hardening modulus and the kinematic hardening rate respectively, ${\dot{\varepsilon }}_{p}$ is the equivalent plastic strain rate.

Finally, the set of hardening material parameters to be identified consists in 5 scalars: the isotropic hardening parameters σ₀, K and n and the kinematic hardening parameters C_A and G_A. Hereafter, due to the homogeneity of uniaxial tensile, shear and reverse shear tests within the samples, a single finite element model was used to simulate these tests. The element BWD3D [46] was selected. It is an 8-node 3D brick element with a mixed formulation adapted to large strains and large displacements. It is based on the non-linear three-field (stress, strain and displacement) Hu–Washizu variational principle [47, 48]. The boundary conditions applied for each test are presented in Fig. 9. In the reverse shear, the loading is reversed once the value of plastic deformation (pre-strain) is reached.

Fig. 9

Boundary conditions applied to model: (a) uniaxial tensile test; (b) simple shear test; (c) reverse shear test; and (d) 2D representation of the reverse shear test

The true tensile stress–strain curve is directly obtained from the FE code. For the shear case, the Hencky shear strain ε_xyH used as a simulation result is computed from the shear angle γ assessed by the imposed displacement ‘U’ and the side length of the square element ‘b’ (Fig. 9d). More details can be found in Appendix A.

SPIF simulations

The capacity of the home-made finite element code Lagamine to model the single point incremental forming process has been checked in previous studies for line tests, cones, pyramids with single or double slopes [49] and materials such as DC01 [20], AlMgSc [1] and AA3003-O [50]. Implicit integration is highly recommended in [51]. The new Z-shape test was designed in the present work (Fig. 5). Inspired by the line test (Fig. 1), it loads the material with more complex stress and strain states because of the presence of corners and the distance between fixed frame and deformed zones. For instance, the maximum triaxiality value T is 1.313 in the line test while it reaches 1.920 in the Z-shape test for the 3 mm depth level (end of step 2 (Fig. 1a) and end of step 4 (Fig. 5) for the line and Z-shape tests respectively). These values are computed by the FE simulations with the final set of parameters identified. The equivalent plastic strain ε_p is also higher for this moment: 6.24% for the line test and 9.02% for the Z-shape test. The whole sheet is modelled for the Z-shape test (Fig. 10b), whereas only the half sheet with a symmetry boundary condition along the X axis is simulated in the line test (Fig. 10a).

Fig. 10

Initial and deformed meshes for: (a) Line test; (b) Z-shape test. Isovalues of Z coordinate field at the end of the simulations for the optimal set of parameters (in mm)

A single layer of an 8-node solid-shell element called ‘RESS’ with three integration points across the thickness was used to mesh the sheet. This element combines the Enhanced Assumed Strain (EAS) method with an in-plane Reduced Integration (RI) scheme. Another solid-shell element with additional Assumed strain modes and combined with the Assumed Natural Strain (ANS) technique called ‘SSH3D’ was also used to model the SPIF process within Lagamine FE simulations. Both element efficiencies were demonstrated in [52] while their comparison is presented in [53]. Due to its lower computation time for a good accuracy, RESS element is chosen here.

The spherical tool is modelled as a rigid body (defined by an analytical equation in the code). It is fixed against rotation as in the experimental set up. To model the contact, the interface elements ‘CFI3D’ [40] based on a penalty approach and a Coulomb’s law were added on the surface of the solid-shell elements. No friction between the tool and the sheet was applied. Finally, the data of the different simulations are summarized in Table 1.

Table 1 Information about the simulations

Material identification and validation

Material data identification

The identification method is summarized by the flowchart of Fig. 11. The iterative Levenberg–Marquardt algorithm selects the successive material input data to decrease the error cost function between FE predictions and experimental measurements. Details about the implemented algorithm, the cost function E, its norm (also a measure of the error) and the extension of the usual method to more than one experiment are presented in Appendix B.

Fig. 11

Flowchart of the identification procedure (E = error between experimental and FE results)

Hereafter, the two tests used to characterize the brass CuZn37 behaviour are the monotonic uniaxial tensile test along RD and the line test loading the material in the out-of-plane direction. Due to their sensitivities to the material parameters, the quantities exploited from the experiments and calculated by the finite element code are the tensile stress–strain curve (Fig. 12a) and the vertical component history of the tool force (the axial tool force) (Fig. 12b) for the line test. The latter choice is similar to [50], and has a physical logic as the vertical tool force is very sensitive to the material parameters in the SPIF process, more than the other force components (see [54]).

Fig. 12

Comparisons of: (a) identified uniaxial stress–strain curve and experimental one and (b) predicted force and measured one within the line test

In the first application of the identification method, the hardening model includes the Ludwick’s isotropic hardening law and the Zielger’s kinematic hardening law. It is called Mix Hard case. For comparison purposes, a second application was limited to isotropic hardening, without kinematic hardening (named Iso Hard). Thus, the effect of the kinematic hardening is investigated by the model choice. Table 2 and Table 3 summarize respectively the role of each numerical test and the identified set of parameters while Fig. 12 compares both results (Mix Hard and Iso Hard) as well as the experimental data for tensile and line tests. The results show a good agreement between the numerical results of Mix Hard case versus the experimental ones. They confirm the presence of the kinematic hardening phenomena in the fourth step (second pass) in the line test.

Table 2 Numerical tests use (Identification/ Validation) and target results

Table 3 Identified material parameters based on the stress–strain curve from a tensile test and the force history of a line test

Figure 12 clearly displays the superiority of the use of Mix Hard model (mixed isotropic and kinematic hardening) to predict the elasto-plastic behavior of the brass CuZn37. The level of the force is almost the same for the first pass for Mix and Iso models. However, significant differences are shown in the second pass. This result confirms the activation of the Bauschinger effect in the second pass of the tool path where the same material points are loaded with a reverse stress path. A relative difference between experimental and computed values on the second pass is shown in Fig. 12b to quantitatively measure the kinematic hardening effect on the second pass by comparing both models Mix Hard and Iso Hard to the experiment.

Validations of the Mix Hard and Iso Hard models and their identified material parameters

The Z-shape test was used as a first validation of the obtained set of material parameters (Fig. 13). This forming process generates a more complex loading path compared to the line test as underlined in "SPIF simulations" section. Results show a good agreement between the prediction of the numerical model (Mix Hard and its material data set) and the experiment, which confirms the efficiency of the mixed hardening model to predict the elasto-plastic behaviour of the brass CuZn37.

Fig. 13

Validation of FE results with Mix Hard and Iso Hard models for the Z-shape test (the numbers define the steps of the tool path see Fig. 5)

For both the Z-shape test and the line test, the force level is almost the same for Iso Hard and Mix Hard models in the first pass of the tool (steps: 1–2-3–4 of the Z-shape test and steps 1- 2 for the line test). Although the tool paths are different for line and Z-shape tests, kinematic hardening effect is clear on the second pass of the tool (steps: 5–6-7–8 of the Z-shape test and steps 3–4 for the line test).

Moreover, the simple monotonic shear test (Fig. 14) was used as a second validation. In this case, the results show that the evolution of the shear stress is almost the same for both models (Mix Hard and Iso Hard).

Fig. 14

Validation with the simple shear test

In monotonic tensile loading (Fig. 12a) and shear loading (Fig. 14), results show a very close agreement between the numerical and experimental curves for both Iso Hard and Mix Hard hardening models. As expected, the accuracy does not depend on the choice of the hardening model for these radial loading tests. The same reasoning applies for the first pass of the Z-shape and line tests. However, the evolution of the stress during a monotonic test relies only on the isotropic hardening for the Iso Hard model, while it relies partly on the isotropic hardening and partly on the kinematic hardening in the Mix Hard model. The identification procedure is able to take this feature into account and generates different optimal values of isotropic hardening parameters (σ₀, K and n) for both models as shown in Table 3.

As a third validation, the reverse shear (Bauschinger) test was simulated. Let us remind that reverse shear testing is a classical test to calibrate a kinematic hardening model [1]. The numerical and experimental results for three different levels of pre-strain (ε_xyH = 10%, ε_xyH = 15% and ε_xyH = 25%) are compared in Fig. 15. The Bauschinger work-hardening stagnation and the elbow area [5] were not targeted in the present paper as they require more advanced hardening models as reminded in Sect. 2.3. However, the reverse yield strengths (A’, B’, C’ in Fig. 15) are satisfactorily predicted by the Mix Hard model. The increased levels of Bauschinger effect for larger pre-strains are quantified in Table 4 and clearly better simulated by Mix Hard law than Iso Hard one, with relative maximal errors of 5% and 38% respectively.

Fig. 15

Comparison of experimental measures and numerical predictions of the Bauschinger effect by Mix Hard (‘1) and Iso Hard laws (‘2)

Table 4 Measured and computed values of the shear yield stresses (MPa) in the direct (A B C) and reverse loading (A’ B’ C’) and their relative error

Sensitivity analysis

In this section, a mathematical approach is used to quantify the sensitivity of the simulation results to each material parameter for the different tests performed. Not only the tensile and the line tests are addressed in the idea to check, if another choice would have been more appropriate within the identification approach. Hereafter, the sensitivity matrix is computed for the Mix Hard case (5 material parameters θ_j: 3 for isotropic hardening and 2 for the kinematic hardening). A representative sensitivity scalar per parameter and per test is computed to allow an easy ranking of the tests.

According to [55], the components of the non-dimensional sensitivity matrix at the abscissa t_i (measure point in the time scale) are defined by the following relation:

$${S}_{ij}=\frac{\partial f({t}_{i},{\theta }_{j})}{\partial {\theta }_{j}}\frac{\Delta {\theta }_{j}}{SC}$$

(3)

where $\frac{\partial f\text{\hspace{0.05em}}({t}_{i},{\theta }_{j})}{\partial {\theta }_{j}}$ is the derivative of the numerical target result f with respect to the parameter ${\theta }_{j}$ at time ${t}_{i}$. Each term is evaluated with the identified set of parameters of the Mix Hard model of Table 3. The dimensional scaling parameters ${\Delta \theta }_{j}$ and $SC$ are the uncertainty range of the parameter ${\theta }_{j}$ and a typical magnitude of the numerical response respectively. According to [55], if there is no information about ${\Delta \theta }_{j}$, the value of the parameter itself can be used. In this work, based on [7], the maximum value of the numerical response is used for the parameter $SC$.

The influence of the parameter ${\theta }_{j}$ expressed within the sensitivity matrix during one whole test is quantified by a scalar called the sensitivity ranking ${\delta }_{j}$ computed by the following equation:

$${\delta }_{j}=\frac{1}{N}\sum_{i=1}^{N}|{S}_{ij}|$$

(4)

where N is the number of measurement points during the test (or taken into account). The average of the absolute value of S_ij was used as an alternative to the maximum of the absolute value as it is more representative of the whole test. ${\delta }_{j}$ gives an indication about the influence of the parameter ${\theta }_{j}$ on the simulation result chosen as representative (stress–strain curves for tensile, monotonic shear and reverse shear tests, vertical component of the punch force components in line and Z-shape test). A high value of ${\delta }_{j}$ means that the parameter ${\theta }_{j}$ has a large influence on the numerical result, while a zero value indicates that the latter is independent from this parameter. Indeed, if a parameter ${\theta }_{j}$ generates a zero or low value of ${\delta }_{j}$ for a test, this test should be removed from the potential experimental candidates in the identification process of ${\theta }_{j}$.

Figure 16 shows the sensitivity ranking of each test for all the material parameters and the identification method reliability. Moreover, a focus on the study of the sensitivity of the vertical force to the kinematic hardening material parameters (${C}_{A}$ and ${G}_{A}$) in SPIF line and Z-shape test cases is presented in Fig. 17a and b. The levels of the reverse shear test (10% of pre-strain) expressed by the sensitivity ranking are lower than those of the SPIF tests (Fig. 17c).

Fig. 16

Sensitivity ranking of the numerical responses for different tests to the material parameters of the Mix Hard model (an average on the whole test was used)

Fig. 17

Sensitivity ranking evolution for: (a) Line test, (b) Z-shape test, (c) RSH 10%

All the numerical results ($\sigma -\varepsilon$ for the tensile test; ${F}_{z}-{\text{time}}$ for the line and Z-shape tests; ${\sigma }_{xy}-{\varepsilon }_{xyH}$ for the shear and reverse shear tests) show a sensitivity of the predictions to the different material parameters but with different amplitudes. Shear and reverse shear tests are the most sensitive ones to K parameter which describes the slope of the isotropic hardening curve in the uniaxial loading. The tensile test and SPIF tests are less sensitive to this K parameter. The line and Z-shape tests are the dominant ones in the sensitivity to the yield strength parameter ${\sigma }_{0}$. All the tests are sensitive to the hardening exponent n with almost the same degree. For kinematic hardening ${C}_{A}$ and ${G}_{A}$, the line test is the most sensitive test and the Z-shape test is in a second position. The spotlight of Fig. 17a and b specially points at the second pass of the tool in the line and Z tests confirming that the sensitivity of the SPIF tests to the kinematic hardening parameters is localized in their second pass. Both Figs. 16 and 17 confirm the interest of the line test to calibrate the kinematic hardening parameters.

The low sensitivity of the reverse shear tests does not affirm that these tests are not sensitive to the kinematic hardening phenomena. The sensitivity to this phenomena mostly appears on the elbow area in the reverse loading. As recommended by [5] and confirmed by Fig. 17c, if the reverse shear test is used to calibrate the kinematic hardening, the identification should use high weighting factors in this area. In the present work, no weight on any point was applied within Eq. (4) computing sensitivity factor or cost function.

Conclusions

In this research, when no shear test or DIC equipment is available, an alternative method for the identification of material parameters of an elasto-plastic sheet metal mechanical behavior is proposed. The Levenberg–Marquardt algorithm is applied on a cost function coupling the results of two experimental tests and FE simulations. The growth of the isotropic von Mises yield surface is depicted by the Ludwick’s law while Ziegler’s law is used to describe the evolution of the back-stress. The choice of a uniaxial tensile test and a line test (a simple case of Single Point Incremental Forming process) generates stress states sensitive to both isotropic and kinematic hardening parameters. These two tests have also the interest to activate both in-plane and out of plane sheet behaviour as well as to provide information on through thickness shear. The identified set of parameters is validated on the Z-shape SPIF test and classical monotonic shear and reverse shear tests.

Without surprise, the application on brass presenting kinematic hardening provides values of the cost function (difference between FE simulations and experimental measurements) higher for the ‘Iso Hard’ (isotropic hardening rule) model than the ‘Mix Hard’ one (isotropic and kinematic rules).

The performed sensitivity analysis quantifies the impact of each material parameter on the results within simulations. This study helps to rank the tests versus the different material parameters to identify.

Some conclusions of this work can be synthesized as follows:

• The robustness of the Levenberg-Marquadt algorithm is confirmed for more than one experimental test allowing the identification method to cover different loading states.

• The Bauschinger effect in the brass CuZn37 material is clear from experimental and numerical points of view. The superiority of the ‘Mix Hard’ model to represent the experimental curves in all the simulated tests confirms the need of kinematic hardening.

• The sensitivity indices of the line test simulations quantify its sensitivity to the target material parameters and specifically the kinematic parameters. The Bauschinger effect on the second pass of the tool within the line test is confirmed by the discrepancy of the Iso Hard simulation and experimental results, and its amplitude is mathematically evaluated by the sensitivity indices related to the parameters of the kinematic hardening rule (${C}_{A}$ and ${G}_{A}$).

• The presence of the work-hardening stagnation in the brass CuZn37 is shown. This phenomena is not possible to depict using a simple kinematic hardening rule as Ziegler’s one. A more advanced model like for instance the Teodosiu-Hu’s hardening law [36] should be used to model this phenomenon.

This methodology is still restricted to isotropic material law. A sensitivity ranking analysis with Hill model was performed on the line test. Its results proved very low sensitivity of most anisotropy parameters. Therefore, identifying Hill model with the line test is not relevant. In ongoing work using SPIF cone test for large strain model identification, Hill parameters are determined based on Lankford coefficients (the classical approach).

Appendices

Appendix A Post processing of the measurements

The automatic post-processing from the tensile machine provides the engineering or nominal stress–strain curve (${\sigma }_{n}-{\varepsilon }_{n}$). As the input parameters required for the FE simulations performed by the Lagamine FE code are the true stress-true strain curve ($\sigma -\varepsilon$), a classical conversion from engineering measurements to the true ones is mandatory.

In uniaxial tensile test along x axis (Fig. 9a) the Cauchy (true) stress ${\varvec{\upsigma}}$ can be written as follows:

$$\sigma=\begin{pmatrix}\sigma_{xx}&0&0\\0&0&0\\0&0&0\end{pmatrix}\;\mathrm{and}\;\sigma_{xx}=\frac{F_{vert}}{S_{act}}$$

(A.1)

where ${F}_{\text{vert}}$ is the vertical force and ${S}_{act}$ is the current cross-sectional area of the specimen which decreases during the loading. The true strain is defined in one dimension by:

$$\varepsilon ={\int }_{{l}_{0}}^{{l}_{f}}\frac{dl}{l}=\mathrm{ln}(\frac{{l}_{f}}{{l}_{0}})$$

(A.2)

where ${l}_{0}$ and ${l}_{f}$ are the initial and final length of the gauge zone respectively and l is its current length. The nominal strain is just defined as ${\varepsilon }_{n}={~}^{\Delta l}\!\left/ \!{~}_{{l}_{0}}\right.$, where $\Delta l$ defines the length variation.

In one dimension, adopting the assumption of volume conservation, analytical expressions for converting (${\sigma }_{n}-{\varepsilon }_{n}$) to ($\sigma -\varepsilon$) are given below:

$$\begin{array}{cc}\varepsilon =\mathrm{ln}(1+{\varepsilon }_{n});& \sigma ={\sigma }_{n}(1+{\varepsilon }_{n})\end{array}$$

(A.3)

Simple shear and reverse shear tests were performed with the bi-axial machine (see Fig. 2b). After the clamping of the specimen, an imposed displacement of the horizontal piston (y direction) is applied (see Figs. 2b and 9d). The Cauchy stress tensor ${\varvec{\upsigma}}$ can be written as follows in this case:

$$\sigma =\left(\begin{array}{ccc}{\sigma }_{xx}& {\sigma }_{xy}& 0\\ {\sigma }_{yx}& {\sigma }_{yy}& 0\\ 0& 0& 0\end{array}\right)$$

(A.4)

with

$$\begin{array}{ccc}{\sigma }_{xx}=\frac{{F}_{vert}}{S}& \mathrm{and}& {\sigma }_{xy}=\frac{{F}_{hor}}{S}\end{array}$$

(A.5)

where ${F}_{\text{vert}}$ and ${F}_{hor}$ are the measured load on the vertical and horizontal pistons respectively, $S$ is the current cross-sectional area of the specimen. ${\sigma }_{yy}$ cannot be directly retrieved from the experiment. It results from a FE computation. Which induces for this elasto plastic case, the choice of a yield locus, a hardening model and boundary conditions.

The deformation gradient F in the simple shear can be expressed by a function of the shear angle $\gamma$ defined in Fig. 9d, in large strain field as follows:

$$F=\left(\begin{array}{ccc}1& 0& 0\\ \mathrm{tg}(\gamma )& 1& 0\\ 0& 0& 1\end{array}\right)$$

(A.6)

VIC 3D software provides Hencky (Logarithmic) strain as a deformation measure. However, the shear angle $\gamma$ (Fig. 9d), computed by the finite element code and the component ${\varepsilon }_{xy}$ of the measured Hencky strain tensor, averaged in VIC 3D, can easily be related. Indeed, Hencky strain tensor is defined by Eq. (A.7) as follows:

$${{\varvec{\upvarepsilon}}}_{\mathrm{H}}=\frac{1}{2}\mathrm{ln}\left({\mathbf{F}}^{\mathrm{T}}\mathbf{F}\right).$$

(A.7)

Appendix B Inverse modelling based on Levenberg-Marquardt algorithm

The inverse modelling is mainly based on an iterative process between experimental measurements and numerical predictions. Experimental tests are performed to provide some relevant physical results and their evolutions. FE analyses simulate the tests and assess the sensitivity of the results to the different material parameters. The minimization of a cost function quantifying the differences between experimental and numerical results, iteratively identify the set of material parameters for the selected constitutive law within the simulation. Figure 11 presents the general concept of the identification strategy applied in this study, where the Levenberg Marquardt (LM) algorithm [16] is selected.

For a single experiment, the Levenberg–Marquardt (LM) algorithm minimizes the sum of the squares of the differences between the experimental and numerical curves by a sequence of updates of the set of parameter values. In Table 2, the target curves (tensile stress strain curve and vertical tool force history of the line test) are defined. The objective function, often nonlinear, depends on several variables. The algorithm combines two methods: the gradient descent method and the Gauss–Newton method. More details about these two methods are provided in [56]. LM is more stable than Gauss–Newton as it may solve the problem even if the start (or the trial) set of variables is far from the solution. However, for some cases, LM may converge slightly slower [57]. The objective function E to minimize is written as follows:

$$E({\varvec{\uptheta}})=\sum_{i=1}^{N}{[{y}_{i}-f({t}_{i},{\varvec{\uptheta}})]}^{2}$$

(B.1)

where ${\varvec{\uptheta}}$ is the vector of material parameters (see Table 3), N is the number of the experimental points used within a single test, ${y}_{i}$ are the ordinate of the experimental curve, ${t}_{i}$ are the abscissa and $f({t}_{i},\theta )$ are the predicted values of the ordinate computed by Lagamine simulations) which depend on the set of parameters to identify ${\varvec{\uptheta}}$. E is a positive value, measure of the difference between the experiment and the FE simulation.

LM is an iterative algorithm. An initial set of parameters supposed to be a good guess of the final parameter set is chosen. These parameters constitute the vector ${\varvec{\uptheta}}$ of the first iteration. To ensure the feasibility of the finite element simulations, this vector should have a physical meaning. Hence, constraints are added to the initial problem to avoid nonphysical solutions. In this spirit, extra functions are implemented in the developed code to specify the field domain for each variable.

At each iteration, the vector ${\varvec{\uptheta}}$ is updated with a new estimation $\theta +\Delta \theta$ obtained by the classical Levenberg–Marquardt formula:

$$({\mathbf{J}}^{\mathrm{T}}\mathbf{J}+\lambda \mathbf{D})\Delta {\varvec{\uptheta}}\approx {\mathbf{J}}^{\mathrm{T}}(\mathbf{y}-\mathbf{f}({\varvec{\uptheta}}))$$

(B.2)

where y and f are the vectors expressing the target curve, experimentally measured or numerically computed respectively, D is the identity matrix, $\lambda$ is a positive damping factor of Levenberg–Marquardt method and J is the Jacobian of the function f with respect to ${\varvec{\uptheta}}$.

The damping factor $\lambda$ could be adjusted at each iteration. If the objective function E promptly decreases, a low value is used for $\lambda$ (the algorithm will be closer to that of Gauss–Newton method). However, if an iteration is not very successful, $\lambda$ is increased, (the algorithm is close to the descent gradient method). More details about the choice and the update of this factor are given in [58, 59].

The convergence of the minimization of E is assumed reached when the numerical curve is in close agreement with the experimental curve. A threshold value could be provided by the user to stop the iterative process.

This algorithm requires the calculation of the Jacobian matrix $\mathbf{J}$:

$$\mathbf J=\frac{\partial\mathbf f(\mathbf\theta)}{\partial\mathbf\theta}$$

(B.3)

Different methods to determine $\mathbf{J}$ are detailed in [60, 61]. The simplest way consisting in using the finite difference method is used in this work. The computation of $\mathbf{J}$ requires (P + 1) evaluations of function f (with P the number of parameters to be identified). A first evaluation is performed with the unperturbed parameters followed by P evaluations, one for each perturbed parameter. The required number of simulations to compute the Jacobian matrix is linearly dependent on the number P of parameters to identify. Indeed, it requires one call with the current values of ${\theta }_{j}$ and one call with a perturbed value of each parameter (${\theta }_{j}+{d\theta }_{j}$). The LM algorithm can be developed outside the FE code, which constitutes a main advantage of this method. Within this study, a separate python script has been developed calling the Lagamine FE software, and coding the LM algorithm.

The components ${J}_{ij}$ of the Jacobian matrix are numerically approximated using a forward difference scheme (1^st order accuracy):

$${J}_{ij}=\frac{f({t}_{i},{\theta }_{j}+d{\theta }_{j})-f({t}_{i},{\theta }_{j})}{d{\theta }_{j}}$$

(B.4)

Two main barriers can prevent the convergence of the algorithm: the insensitivity of the numerical response to a parameter and the linear dependency between two parameters. The first obstruction is mathematically interpreted by the existence of a null column in the Jacobian matrix. If there is a linear dependency between the columns of $\mathbf{J}$, the method fails because matrix $\left({\mathbf{J}}^{\mathrm{T}}\mathbf{J}\right)$ called Fisher’s matrix is singular. The rank of $\left({\mathbf{J}}^{\mathrm{T}}\mathbf{J}\right)$ is lower than its dimension (which is equal to the number of parameters). Outside these two barriers, the damping factor $\lambda$ permits to avoid the bad conditioning that is assessed by the ratio of the minimum and maximum eigenvalues of the Fisher’s matrix.

The identification of the material parameters based on more than one test (with different magnitudes) requires extra implementations in the code. The components related to each test of the identification procedure should be normalized in order to be expressed in the same base.

Therefore, the final objective function can be written as follows:

$$E(\mathbf\theta)=\sqrt{\frac1{\sum_{k=1}^{nbtest}N_k}\sum_{k=1}^{nbtest}\sum_{i=1}^{N_k}{\lbrack\frac{y_{ki}-f_k(t_i,\mathbf\theta)}{f_{k\_max}}\rbrack}^2}$$

(B.5)

with nbtest is the number of tests used, k identifies the test and ${N}_{k}$ is the number of the experimental points for the test k. Here nbtest is equal to 2 (tensile and line test).

The normalized version of the former Levenberg–Marquardt formula B. (2) can be expressed as follows:

$$\Delta {\varvec{\uptheta}}\approx {({\widetilde{\mathbf{J}}}^{\mathrm{T}}\widetilde{\mathbf{J}}+\lambda \mathbf{D})}^{-1}[{\widetilde{\mathbf{J}}}^{\mathrm{T}}(\widetilde{\mathbf{y}}-\widetilde{\mathbf{f}}({\varvec{\uptheta}}))]$$

(B.6)

The different components of the B. (6) ($\widetilde{\mathbf{J}}$, $\widetilde{\mathbf{y}}$ and $\widetilde{\mathbf{f}}$) are the relative values defined by dividing each vector by the maximum value of its components. To maintain the same weight for all the tests, an easy way is to select the same number of points ${N}_{k}$ for each test.

$$\begin{array}{c}\begin{array}{cc}\widetilde{\mathbf{y}}=\left[\frac{{\mathbf{y}}_{1}}{{\Vert {\mathbf{f}}_{1}\Vert }_{\infty }};\frac{{\mathbf{y}}_{2}}{{\Vert {\mathbf{f}}_{2}\Vert }_{\infty }};..;\frac{{\mathbf{y}}_{nbtest}}{{\Vert {\mathbf{f}}_{nbtest}\Vert }_{\infty }}\right],& \widetilde{\mathbf{f}}=[\frac{{\mathbf{f}}_{1}}{{\| {\mathbf{f}}_{1}\| }_{\infty }};\frac{{\mathbf{f}}_{2}}{{\| {\mathbf{f}}_{2}\| }_{\infty }};..;\frac{{\mathbf{f}}_{nbtest}}{{\| {\mathbf{f}}_{nbtest}\| }_{\infty }}]\end{array}\\ \widetilde{\mathbf{J}}=[{\widetilde{\mathbf{J}}}_{1};{\widetilde{\mathbf{J}}}_{2};..;{\widetilde{\mathbf{J}}}_{nbtest}]\end{array}$$

(B.7)

To further clarify, these different quantities are presented as follows in matrix form for the “two tests” case:

$$\widetilde{\mathbf{J}}= \left(\begin{array}{ccc}\frac{\partial {\widetilde{\mathrm{f}}}_{1}({\mathrm{t}}_{1})}{\partial {\uptheta }_{1}}& \dots & \frac{\partial {\widetilde{\mathrm{f}}}_{1}({\mathrm{t}}_{1})}{\partial {\uptheta }_{\mathrm{P}}}\\ \begin{array}{c}.\\ .\\ \frac{\partial {\widetilde{\mathrm{f}}}_{1}({\mathrm{t}}_{\mathrm{N}1})}{\partial {\uptheta }_{1}}\end{array}& \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}.\\ .\\ \frac{\partial {\widetilde{\mathrm{f}}}_{1}({\mathrm{t}}_{\mathrm{N}1})}{\partial {\uptheta }_{\mathrm{P}}}\end{array}\\ \begin{array}{c}\frac{\partial {\widetilde{\mathrm{f}}}_{2}({\mathrm{t}}_{1})}{\partial {\uptheta }_{1}}\\ .\\ .\\ \frac{\partial {\widetilde{\mathrm{f}}}_{2}({\mathrm{t}}_{\mathrm{N}1})}{\partial {\uptheta }_{1}}\end{array}& \begin{array}{c}\dots \\ .\\ .\\ .\end{array}& \begin{array}{c}\frac{\partial {\widetilde{\mathrm{f}}}_{2}({\mathrm{t}}_{1})}{\partial {\uptheta }_{\mathrm{P}}}\\ .\\ .\\ \frac{\partial {\widetilde{\mathrm{f}}}_{2}({\mathrm{t}}_{\mathrm{N}2})}{\partial {\uptheta }_{\mathrm{P}}}\end{array}\end{array}\right),\widetilde{\mathbf{y}}= \left(\begin{array}{c}{\widetilde{\mathrm{y}}}_{11}\\ .\\ .\\ {\widetilde{\mathrm{y}}}_{1\mathrm{N}1}\\ {\widetilde{\mathrm{y}}}_{21}\\ .\\ .\\ {\widetilde{\mathrm{y}}}_{2\mathrm{N}2}\end{array}\right),\widetilde{\mathbf{f}}= \left(\begin{array}{c}{\widetilde{\mathrm{f}}}_{1}({\mathrm{t}}_{1})\\ .\\ .\\ {\widetilde{\mathrm{f}}}_{1}({\mathrm{t}}_{\mathrm{N}1})\\ {\widetilde{\mathrm{f}}}_{2}({\mathrm{t}}_{1})\\ .\\ .\\ {\widetilde{\mathrm{f}}}_{2}({\mathrm{t}}_{\mathrm{N}2})\end{array}\right)$$

(B.8)

P is the number of parameters to identify.

The normalized Jacobian matrix is usually calculated using a forward difference scheme but based on the numerical results after the normalization:

$${\widetilde{J}}_{ij}=\frac{\widetilde{f}({t}_{i},{\theta }_{j}+d{\theta }_{j})-\widetilde{f}({t}_{i},{\theta }_{j})}{d{\theta }_{j}}$$

(B.9)

Note: in this work, the normalization of the different quantities was not mandatory since the two used tests in the identification procedure (tensile and line test) have almost the same magnitude.