Introduction

The high mechanical, fatigue and corrosion resistances of Ti6Al4V titanium alloy, coupled with a low density and a good biocompatibility lead to an increase of its use in the aerospace and biomedical fields as machined parts [1]. It is however a hard-to-machine material due to its low thermal conductivity coupled with hardening. Finite element modeling can enhance the comprehension of the phenomena involved in machining. It is also intended to help the practitioner in the choice of the adequate cutting parameters. The development of realistic finite element models requires to model correctly the machined material in extreme conditions of strain, strain rate and temperature. These extreme conditions can, however, not be reached by current experimental means of tests. Indeed, today’s experimental technology does not allow to reach sufficiently high strains and strain rates, moreover at high temperatures except for machining test itself. For example, Lee and Lin [2] provide experimental curves for strains up to 0.25 and strain rates of 2000 s− 1 at temperatures between 973 K and 1373 K, rather low values in modeling of machining for which strains up to 6 can be reached, as well as strain rates of 10E7 s− 1 and rate of temperature gradient of the order of 10E6 K/s when crossing the primary shear zone [3]. The material constitutive models developed based on these tests therefore only represent partially the material behavior in the conditions of the cutting process. The limitations of these constitutive models (currently mostly emprirical models) are particularly observed for the Johnson-Cook model [4], although it is the most used in the field (and consequently also for Ti6Al4V, the machined material considered in this work).

In order to solve this issue, several empirical constitutive models have been introduced recently [4,5,6,7,8]. They, among others, take into account the strain softening, contributing to the formation of segmented (or saw-toothed) Ti6Al4V chip [4, 9]. The parameters of these constitutive models are usually obtained through inverse analysis thanks to the observation of the experimental chips global morphology, their geometrical characteristics and the measured cutting forces. In the end, the user misses objective arguments to choose between these constitutive models in the absence of experimental reference curves due to the practical limits mentioned earlier. Moreover, few comparisons between the results when using different constitutive models are available in the literature [10,11,12].

To fill this gap, this article compares four constitutive models based on the well-known Johnson-Cook flow stress model by introducing them in a finite element model for, in a first time, cutting conditions leading to a segmented chip, the hardest morphology to model. The results are then opposed to an experimental reference obtained in strictly orthogonal cutting conditions in order to highlight the differences they lead to and to provide objective information to choose which flow stress should be adopted for future modeling. The comparison is divided in two steps: firstly, no damage properties are given to the chip to allow the strict comparison of the four flow stresses. Secondly, damage is added in the chip to obtain more realistic morphologies and take the experimental observations during chip formation into account. The experimental – numerical comparison is focused on the data that are the most used and measured in practice: the chip morphology and the cutting force. In a second time, the cutting conditions are changed to provide continuous chips. The numerical results are compared to the experimental reference to show that the same model is able to predict the difference in the chip formation.

Experimental reference

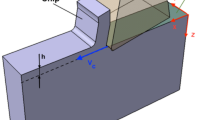
The results from the experimental orthogonal cutting tests introduced in Ducobu et al. [13] were adopted to have an experimental reference in strictly orthogonal cutting and in the same cutting conditions as the numerical model. Titanium alloy Ti6Al4V grade 5 (ASM 4928, chemical composition in Table 1) at the classic state used in the aerospace industry (annealed at 750 ∘C for one hour followed by air cooling) was adopted for the experiments. The microstructure of the base material is provided in Fig. 1. The setup used a standard milling machine as a planning machine [13]. The machined sample is inserted into the spindle and the tool is fixed with a custom made support part on the force sensor, itself on the machine table. The cutting movement is the sample horizontal displacement with respect to the stationary tool (Fig. 2). This leads to the removal of a layer of material of constant and user-defined thickness in strictly orthogonal cutting conditions. In this configuration, the maximal achievable cutting speed is set by the maximal feed rate of the milling machine; typically of the order of 20 m/min to 30 m/min. The cutting length and the width of cut are set by the dimensions of the feature to machine, a 10 mm long and 1 mm wide tenon [13]. This cutting length is large enough for the process to be steady and the forces to be measured, while it is short enough to prevent the chip to roll up [13]. The chips can therefore be embedded without unrolling, and there is no error on the measured lengths due to the unrolling distortions. A width of 1 mm minimizes the efforts in the spindle bearings and it directly gives the forces value per mm width as in 2D plane strain numerical models (with a width of cut by uncut chip thickness ratio larger than 3 for the adopted values, to respect plane strain assumptions). The rake angle is 15∘, the clearance angle 2∘ and the cutting edge radius 10 μm. The cutting speed is fixed at 30 m/min (i.e. the maximum feed rate of the machine). Four different uncut chip thickness values are adopted (Table 2): h = 280 μm (6 repetitions in the experiments) leads to a segmented chip, while h = 40 μm, 60 μm and 100 μm (3 repetitions in the experiments) lead to a continuous chip. Although the cutting speed also influences the chip formation and its morphology [14], only the uncut chip thickness varies in this study. Indeed, the experimental setup limits the maximum cutting speed to the maximum feed rate of the machine (30 m/min in this case), which does not allow to modify significantly the cutting speed while keeping it in an industry relevant range.

Table 1 Chemical composition in weight percent of Ti6Al4V grade 5 (ASM 4928) [15]
Full size table
Fig. 1
figure 1

Microstructure of the base material

Full size image
Fig. 2
figure 2

Orthogonal cutting configuration on the milling machine [13]

Full size image
Table 2 Cutting conditions of the experiments
Full size table

Numerical model

General features

The numerical model consists of a 2D plane strain explicit Lagrangian orthogonal cutting model developed with the commercial software ABAQUS/Explicit v6.14-2. Similarly to the current literature, it models the area close to the cutting edge of the tool. The workpiece is modeled as a rectangular block of 1 mm long and 0.75 mm high; the tool has the same geometry as for the experiments. These two parts are meshed with four-node CPE4RT linear elements (the model is composed of nearly 8500 elements). Figure 3 presents the structured mesh grid of the model at the beginning of the cut. Elements of 10 µm × 5 µm are used to mesh the chip, while rectangular elements of increasing length when moving away from the cutting region are adopted for the area under the chip. The sacrificial layer (cf. 2) is composed of square elements of 10 µm side (i.e. the cutting edge radius value). The workpiece is fixed in space while the tool moves horizontally at the cutting speed (30 m/min).

Fig. 3
figure 3

Mesh topology

Full size image

The workpiece material, Ti6Al4V, is assumed to be homogeneous. It is described by four different empirical constitutive models, detailed in the next paragraph. The tool material, tungsten carbide, is also homogeneous and is described by a linear elastic model. Coulomb’s friction is used to model friction at the tool – chip interface with a low coefficient value (0.05) in accordance with Bäker et al. [16] and Calamaz et al. [4]. Although tool – chip contact is a key parameter in cutting, in this paper, the Coulomb model approach, one of the most used models (in Arrazola and Özel [17], Mabrouki et al. [18] for example), is considered in order to focus the attention on the material constitutive model and as qualitative information is sought. All the friction energy is converted into heat and this heat flows equally to the workpiece and the tool (classic assumptions [17, 19]). Contact heat transfer is allowed at the tool – chip interface. The heat conduction coefficient (Table 3) was chosen to reach quickly thermal steady-state thanks to the rapid temperature rise in the tool, while providing a temperature discontinuity between the chip and the tool as the heat transfer is not perfect. The workpiece and tool initial temperature is set to 25°C (298 K).

Table 3 Material properties and cutting conditions of the numerical model [4, 13, 15, 20, 21]
Full size table

Constitutive models

Four empirical constitutive models are considered in this work to represent the behavior of Ti6Al4V. It is important to mention that no information on the material state and treatments is provided by the authors in the papers introducing these models. The identification of the material parameters may therefore have been carried out on a material with a different metallurgical state.

The first constitutive model is the Johnson-Cook (JC) model, the most adopted model in machining modeling. The flow stress depends on strain, strain rate and temperature. It is described by three multiplicative distinctive terms. They represent, respectively, the strain hardening, the strain rate hardening and the thermal softening behaviors of the material [22]:

$$ \sigma = \left[A + B\ \varepsilon^{n} \right] \left[1 + C\ \ln\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{0}}\right] \left[1 - \left( \frac{T - T_{room}}{T_{melt} - T_{room}}\right)^{m}\right] $$
(1)

Where Tmelt is the melting temperature of the workpiece material, Troom is the room temperature, ε is the plastic strain, \(\dot {\varepsilon }\) is the plastic strain rate and \(\dot {\varepsilon }_{0}\) is the reference plastic strain rate. Material constant A is the yield strength, B is the hardening modulus, C is the strain rate sensitivity, m is the thermal softening exponent and n is the strain-hardening exponent. Table 4 gives the set used for this study. According to Meyer and Kleponis [23], the parameters were determined at strain rate levels of 0.0001 s− 1, 0.1 s− 1 and 2150 s− 1 and at a maximum plastic strain of 0.57. Many sets leading to very different stress – strain evolutions are available in the literature [24]. These JC parameters were chosen as the value of parameter A, 862.5 MPa, is equal to the yield stress of Ti6Al4V at room temperature [23], which is consistent with the description of the Johnson-Cook constitutive model. It was furthermore estimated as the most popular and frequently found in literature. The main drawbacks of JC flow stress are its inability to represent high strain behavior and the uncoupled effect of strain, strain rate and temperature [7].

Table 4 Parameters of the four empirical constitutive models [4, 6, 7, 23]
Full size table

The second flow stress model is the TANgent Hyperbolic (TANH), which is a JC model modified by Calamaz et al. [4] to take into account the strain softening phenomenon that would be necessary to produce segmented Ti6Al4V chips. Indeed, according to Calamaz et al. [4], the JC model correctly represents the behavior of Ti6Al4V up to strain rates of 1000 s− 1 and strains of about 0.3. These values are smaller than what is encountered in machining: strain can be as large as 6 and strain rates as 107 s− 1 [3]. Moreover strains larger than 0.5 would lead to the strain softening phenomenon, which was identified in the literature as one of the causes responsible for the formation of segmented Ti6Al4V chips [9]. The physical phenomena at the origin of this strain softening are not known yet but dynamic recrystallisation (mainly in the β phase field) could be the main reason according to Ding et al. [25]. The strain softening is taken into account via the fourth term introducing the tangent hyperbolic function [4]:

$$ \begin{array}{@{}rcl@{}} \sigma & = & \left[A + B\ \varepsilon^{n} \left( \frac{1}{\exp{(\varepsilon^{a})}} \right) \right] \\ & & \left[1 + C\ \ln\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{0}}\right] \left[1 - \left( \frac{T - T_{room}}{T_{melt} - T_{room}}\right)^{m}\right] \\ & & \left[E + (1 - E) \tanh\left( \frac{1}{(\varepsilon + S)^{c}} \right) \right] \end{array} $$
(2)

with

$$ \begin{array}{@{}rcl@{}} E = 1 - \left( \frac{T}{T_{melt}} \right)^{d} & \text{and} & S = \left( \frac{T}{T_{melt}} \right)^{b} \end{array} $$

Parameters A, B, C, m and n have the same meaning as for JC, while a, b, c and d are new ones introduced by TANH. Parameters a and c modify the slope of the stress drop, a at high strain and c at low strain. The maximal stress value is controlled by b. Parameter d influences the magnitude of the strain softening: a high value gives a weak strain softening. The decrease of the maximal stress value when temperature increases is taken into account by S, which depends on the temperature. The introduction of the tangent hyperbolic does not alter stresses at low strains (corresponding to experimental values) and adds softening at high strains. The set of parameters of the TANH model comes from Calamaz et al. [4] and is given in Table 4.

The third constitutive model is a second version of TANH, called TANH2 in this article. According to Calamaz et al. [6], it improves the first TANH formulation in the sense that the strain softening appears from approximately Trec (approximately 30% of the melting temperature) and not at room temperature anymore, as shown by experimental results reported by Calamaz et al. [6]. This law is expressed as [6]:

$$ \begin{array}{@{}rcl@{}} \sigma & = & \left[A + B\ \varepsilon^{n} \right] \left[1 + C\ \ln\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{0}}\right] \left[1 - \left( \frac{T - T_{room}}{T_{melt} - T_{room}}\right)^{m}\right] \\ & & \left[F + (1 - F) \tanh\left( \frac{1}{\varepsilon + \varepsilon_{0}} \right) \right] \end{array} $$
(3)

with

$$ \begin{array}{@{}rcl@{}} F = 1 - \left[\frac{p\ \varepsilon}{1 + p\ \varepsilon} \tanh\left( \frac{T - T_{room}}{T_{rec} - T_{room}} \right)^{q} \right] \end{array} $$
(4)

By comparison with TANH, the parameter F (4) now depends on strain and temperature to better describe the strain softening phenomenon. The parameters adopted (Table 4) come from Calamaz et al. [6]. The slope of the curve after the maximal stress is controlled by parameter p. The onset temperature for the strain softening phenomenon is Trec and parameter q influences the temperature range affected by the strain softening. The additional parameters, by comparison with JC, of both TANH models were obtained by Calamaz et al. through inverse analysis based on experimental cutting results.

The fourth model is another modification of TANH by Sima and Özel [7] (called Sima flow stress in this article). This consists of a TANH model with a better control on the thermal softening trough tangent hyperbolic function [7]:

$$ \begin{array}{@{}rcl@{}} \sigma & = & \left[A + B\ \varepsilon^{n} \left( \frac{1}{\exp{(\varepsilon^{e})}} \right) \right] \\ & & \left[1 + C\ \ln\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{0}} \right] \left[1 - \left( \frac{T - T_{room}}{T_{melt} - T_{room}} \right)^{m} \right] \\ & &\left[G + (1 - G) \left\{\tanh\left( \frac{1}{(\varepsilon + R)^{g}} \right) \right\}^{r} \right] \end{array} $$
(5)

with

$$ \begin{array}{@{}rcl@{}} G = 1 - \left( \frac{T}{T_{melt}} \right)^{h} & \text{et} & R = \left( \frac{T}{T_{melt}} \right)^{f} \end{array} $$

The parameters of this constitutive model (Table 4) are given by Sima and Özel [7]. The strain hardening is controlled by parameter e by decreasing the flow stress after a critical strain value. The parameter f controls the temperature-dependent softening and at which the maximum stress occurs. Parameter h has a strong impact on the stress value and sets its minimum. Parameters g and r have interacting but similar effects on the stress. With f, g, h, the parameter r controls the tanh function in thermal softening at elevated strains and temperatures. It also influences the softening trend. The TANH, TANH2 and Sima models were introduced in Abaqus in the form of a table linking the stress, the strain, the strain rate and the temperature.

The four constitutive models are plotted at a strain rate of 15,000 s− 1 and a temperature of 400 K (below Trec = 600 K) in Fig. 4 and a temperature of 800 K (above Trec) in Fig. 5. When the temperature is higher (Fig. 5), lower stresses are observed, as expected due to the thermal softening. JC and TANH2 flow stresses are similar under Trec, although the stress magnitude is different. Above Trec, the strain softening effect is activated for TANH2 model; its shape is however different from TANH and Sima models as the stress decrease is more progressive. The shapes of TANH and Sima flow stresses are quite close to each other, the main difference being the magnitude of the stresses and the strain softening occurring at lower strain for TANH. The comparison between JC and TANH models at 400 K clearly shows the influence of the strain softening on the level of the stresses. They are close to each other at very low strains, then the difference increases with strain due to the strain softening. A similar observation is made for TANH2 and Sima models: stresses are close at low strain and differ at high strains. This difference decreases when strain increases for temperature above Trec. Two groups can be made based on the stress magnitude before the activation of strain softening (i.e. at low strain): JC and TANH on one hand and TANH2 and Sima on the other hand. This difference in the stress magnitude is mainly due to the large difference in the value of parameter B.

Fig. 4
figure 4

Flow stress curves at 400 K and 15,000 s− 1

Full size image
Fig. 5
figure 5

Flow stress curves at 800 K and 15,000 s− 1

Full size image

To conclude on the constitutive models, different cutting forces magnitudes can be expected as different stresses levels are noted. The shapes of the flow stresses should also influence the chips morphologies. The differences of the JC parameters among the four models are quite significant. Figures 4 and 5 clearly show that there is a need to specify the state of the material in future research aiming at the identification of material models parameters. Current available information may lead to the comparison of materials with different metallurgical state inducing differences in the results. The need to specify the metallurgical state of the material when identifying the parameters of the constitutive model has already been mentioned in the particular case of the Johnson-Cook model [24]. For TANH, TANH2 and Sima constitutive models, less different sets of parameters are available in the literature than for JC model. The values of the parameters used in this study come from the articles introducing these three models, Calamaz et al. [4], Calamaz et al. [6] and Sima and Özel [7], respectively. This allows to reach the goal of the current study: assessing the performance of each constitutive model with the “original” set of parameters with which it was developed and comparing them with the reference model of Johnson-Cook.

Material damage modeling

Due to the Lagrangian formulation, a chip separation criterion is needed to allow the chip formation. An “eroding” element criterion based on crack propagation depending on the stress and strain state of the machined material is adopted. This chip formation approach, by ductile failure phenomenon, is in agreement with the experimental findings of Subbiah and Melkote [26]. It is composed of two steps. In the first one, a damage initiation criterion must be fulfilled. The second step concerns damage evolution, based on the fracture energy approach. This kind of chip formation modeling has been introduced by Mabrouki et al. [27] for AISI 4340 and the ALE formalism. Mabrouki et al. [28] then modified the workpiece geometry to introduce a chamfer and reduce the mesh distortion and optimize contact management for Al2024-T351. Mabrouki et al. [18], Zhang et al. [29] and Chen et al. [30] adopted the same model for Ti6Al4V with the Johnson-Cook constitutive model (without chamfer on the workpiece for Chen et al. [30]).

The damage initiation criterion is the Johnson-Cook shear failure model [31]. The initiation of damage is computed in each element by

$$ \omega = \sum \frac{\varDelta \varepsilon}{\varepsilon_{D = 0}} $$
(6)

In which Δε is the increment of equivalent plastic strain, εD= 0 is the equivalent plastic strain when damage is initiated (ω = 1). It is computed with the Johnson-Cook shear failure model [31]:

$$ \begin{array}{@{}rcl@{}} {\varepsilon}_{D = 0} & = & \left[D_{1} + D_{2}\ \exp\left( D_{3}\ \sigma^{*}\right) \right] \left[1 + D_{4}\ \ln\frac{\dot{\varepsilon}}{\dot{\varepsilon}_{0}}\right] \\ & & \left[1 - D_{5} \left( \frac{T - T_{room}}{T_{melt} - T_{room}}\right)\right] \end{array} $$
(7)

With \(\sigma ^{*} = \frac {\sigma _{m}}{{\sigma }}\) the stress triaxiality, σm the mean stress and σ the equivalent Von Mises stress. Variables D1 to D5 are the shear failure model parameters and the other variables have the same meaning as for the Johnson-Cook flow stress model. Their values are given in Table 5.

Table 5 Johnson-Cook failure model parameters [32]
Full size table

In order to reduce the mesh dependence to localization during damage evolution (after the damage initiation criterion has been reached), fracture energy during crack propagation [33], Gf, is introduced to represent the stress-displacement relation rather than the stress-strain relation:

$$ G_{f} = {\int}_{\varepsilon_{D = 0}}^{\varepsilon_{D = 1}} L_{c} \sigma {d\varepsilon} = {\int}_{0}^{u_{D = 1}} \sigma \mathrm{d}u $$
(8)

With Lc the element characteristic length and u the equivalent displacement. Before the onset of damage, u = 0 and after, u = Lcε. The element characteristic length depends on the element geometry. For plane elements, it is defined as the square root of the element surface [34]. The fracture energy Gf is the required energy to open a unitary area crack. In plane strain, it is given by

$$ G_{f} = \frac{1 - \nu^{2}}{E} {K^{2}_{C}} $$
(9)

Where ν is Poisson’s ratio, E is Young’s modulus, KC is fracture toughness in mode I (KIC) [35]. The evolution of damage, D, can be either linear

$$ D = \frac{L_{c}\ \varepsilon}{u_{D = 1}} = \frac{u}{u_{D = 1}} $$
(10)

either exponential

$$ D = 1 - \exp\left( -{\int}_{0}^{u_{D = 1}} \frac{\sigma}{G_{f}} \mathrm{d}u\right) $$
(11)

The value of D goes from 0 when damage is initiated (and ω = 1) to 1 at material failure. As soon as the specified value of Gf is reached in a finite element, it is deleted and all of its stress components are put to zero. The suppression of a finite element introduces a crack in the workpiece, making it possible for the chip to come off. In this model, the chip separation is assumed to occur along a predefined straight path composed of one element in height. Damage properties with linear evolution [18, 29] are therefore given only to this part of the workpiece, typically called “sacrificial layer” [26] (or “separation line” [30]), in a first time to allow the comparison of the four constitutive models. Damage will be introduced in the chip in a second time to obtain a more realistic segmented morphology.

Segmented chip formation with the four constitutive models without damage in the chip

The experimental chips were collected before being embedded into epoxy resin to stand on their edge and polished straight across their length. To characterize the segmented chip geometry, four lengths (highlighted in Fig. 6a) are usually measured [36]: the undeformed segment length L, the height of the segment H, the valley C and the pitch P. The mean values (on 25 segments) of these characteristic lengths are given in Table 7.

Fig. 6
figure 6

a Characteristic lengths of a segmented chip [13], b Experimental chip at h = 280 µm [13]

Full size image
Fig. 7
figure 7

Numerical chips at h = 280 µm without damage in the chip after 600 µs a JC, b TANH, c TANH2 and d Sima, temperature plots (in K)

Full size image

At this stage, the objective is to highlight the differences resulting of only the constitutive models and so no damage properties are given in the chip. The four numerical chips are shown in Fig. 7 after 600 µs of simulation (the steady state for the cutting force and the chip thickness is reached after 200 µs for the modeling). It is clear that they are all far away from the experimental one: none has the geometry of a segmented chip as experimentally observed. It consequently does not make sense to measure their characteristic lengths when looking at the chips morphologies in Figure 7 (continuous or slightly segmented chips). Some differences between the chips are however observed. The chips from JC and TANH2 flow stresses are continuous, while they have small segments with TANH and Sima models. The chip morphology with Sima model is more regular than with TANH for which the first segment is more marked (its valley is lower). From the morphology point of view, these four constitutive models do therefore not allow to form a satisfactory chip.

Differences are also noted on the cutting forces evolutions plotted in Fig. 8 for each numerical case together with the experimental values. These differences are of two types: the shape of the evolution and the magnitude. Two shapes are observed in Fig. 8: nearly constant and with oscillations around a mean value. The forces evolutions are closely linked to the chip morphology. Indeed, the cutting force is nearly constant when the chip is continuous and has a cyclic evolution in regime when it is slightly segmented: the evolutions of the cutting force for JC and TANH2 models are nearly constant and the chips are continuous, while small segments are observed for the two others and their cutting force is not constant anymore. The magnitude of the forces is closely linked to the flow stress: when the level of the stresses is higher, the magnitude of the cutting force is higher as well. The root mean square (RMS) values of the cutting forces (Table 6) confirm it and clearly show that the lower stresses of JC and TANH models result in lower cutting forces than TANH2 and Sima models. Looking back at Fig. 4, it becomes obvious that the absence of small segments in the chip is due to the strain softening not taken into account in the constitutive law or to the temperature too low to activate it (Fig. 5). Table 6 shows that Sima flow stress gives the closest RMS cutting force value to the experiments, with a difference of 12% with the experimental reference.

Fig. 8
figure 8

Comparison of the numerical cutting forces with the experimental RMS value (the thickness of the experimental line represents the standard deviation) at h = 280 µm without damage in the chip, low-pass filter cutoff frequency at 10 kHz

Full size image
Table 6 RMS cutting forces values at h = 280 µm, closest values to experimental reference in bold
Full size table

To conclude this paragraph, the numerical results so far exhibit significant differences with the experiments; the main one being the modeled chips morphologies far from the experimental one. As stated previously, the objective was to compare the four different constitutive models and their ability to produce a realistic chip without damage properties in the chip to provide information related only to the constitutive model. The significant chips morphologies differences mean that, for the cutting conditions adopted, the considered flow stresses alone do not allow to produce a satisfactory chip. TANH and Sima models give results closer to the experiments than JC and TANH2 models but the differences are however significant. Previous experimental [13, 37] and numerical [4, 9] works on Ti6Al4V segmented chips formation showed that a crack propagates inside the primary shear zone and that it should be taken into account to form a chip with a morphology close to the experiments. Damage will accordingly be introduced in the chip.

Inclusion of damage in the chip with the four constitutive models

To model crack propagation in the primary shear zone when a segmented chip is formed, damage is introduced the same way in the chip as in the sacrificial layer: Johnson-Cook damage failure in two steps is used with an exponential evolution of damage parameter D [18, 28]. Figure 9 shows the corresponding four numerical chips after 1350 µs of simulation. More than 600 µs are modeled with damage in the chip in order to have enough segments to measure the characteristic lengths of the chips on more than one segment. All of the chips are different from these without damage and none is continuous anymore. The three chips with a constitutive model taking strain softening into account now exhibit a segmented morphology. With TANH2 and Sima flow stresses, the chips are qualitatively very close. Such a chip with TANH2 model was not expected when looking back at the results without damage. That morphology change is due to the larger deformation in the primary shear band involved by the crack propagation. It induces an increase of the temperature above Trec in the primary shear zone, turning on the strain softening. These chips are now closer to the experimental reference (Figure 6 (b)).

Fig. 9
figure 9

Chips at h = 280 µm with damage in the chip after 1350 µs a JC, b TANH, c TANH2 and d Sima, temperature plots (in K)

Full size image

The characteristic lengths of the segmented chips are given in Table 7. To avoid the influence of a difference in the results between the modelling and the experiments due to the different cutting times (leading to differences in the cutting process and therefore the chip geometry and cutting forces), the same portion of the chip is considered. As can be seen in Fig. 6b, only the first segments of the chip (i.e. where the cutting process is starting) are considered, which is consistent with Fig. 9. The very first segment of each chip is not taken into account as the tool has just entered into the workpiece. The chip with the closest lengths to the experiments is that with Sima model. The undeformed segment length is still underestimated (and equal to that with TANH2 model), while the height of the segments is very close to the experiments; they can be considered as equal due to the standard deviations. The valley is nearly half that of the reference one, indicating that the crack propagates too easily in the primary shear zone. This is even worse with TANH2 model, contrary to the too large, but closer to the experiments, TANH valley. Such a small valley leads to a chip with a low rigidity. Self-contact is not enabled in the model, emphasizing the rolling of the chip on itself. The values of the pitch are therefore only indicative and will not be used in the comparison. It is however not surprising to note that the pitch of the chip with TANH model is larger than with TANH2 and Sima models as its valley (and thus rigidity) is larger.

Table 7 Characteristic lengths with damage in the chip at h = 280 µm (L: undeformed segment length, H: height of the segment, C: valley and P: pitch, experimental measurements on 25 segments), closest values to experimental reference in bold
Full size table

In Fig. 10, it is seen that none of the cutting forces evolutions is constant anymore, in accordance with the chips morphologies. They can be linked to the segments formation: a decrease in the force corresponds to the formation of a segment and the magnitude of the force variation is the image of the size of the segments. This is an important qualitative information, coupled with the capacity of the model to produce realistic segmented chips qualitatively close to the experimental reference. As previously, two levels of magnitude are observed: low with JC and TANH models and high with TANH2 and Sima models, which is confirmed by the RMS values presented in Table 6. The numerical forces are lower than without damage in the chip due to the oscillations caused by the formation of the segments and the larger width of the valleys of the cutting forces, leading to a decrease of the RMS values. All of them are now lower than the experimental reference. The constitutive models leading to the closest cutting forces are Sima and TANH2 with values exhibiting a difference of 22% by comparison with the experimental reference. The addition of damage in the chip therefore brings the morphology close to that of the experiments, while it degrades the prediction of the cutting force RMS value.

Fig. 10
figure 10

Comparison of the numerical cutting forces with the experimental RMS value (the thickness of the experimental line represents the standard deviation) at h = 280 µm with damage in the chip, low-pass filter cutoff frequency at 10 kHz

Full size image

The segmentation frequency, fg is computed from the undeformed segment length, L, and the cutting speed , Vc by [38]:

$$ f_{g} = \frac{V_{c}}{L} $$
(12)

The experimental segmentation frequency is 2427 Hz. The numerical model with Sima flow stress has a segmentation frequency of 3268 Hz. By comparison, the TANH constitutive model leads to a frequency of 5319 Hz. The difference with the experimental value is larger, which was expected as the undeformed segment length is smaller and the frequency of the cutting force variations (Fig. 10) is higher. Moreover, after the same cutting length, more segments are formed with TANH constitutive model by comparison with Sima’s (Fig. 9b and d).

To conclude on the comparison of the four empirical constitutive models considered, the results on the chips morphologies and on the cutting forces show that the closest geometry and the closest RMS value of the cutting force are obtained with Sima flow stress. It is therefore the most suited model to represent Ti6Al4V in machining modeling for the cutting conditions adopted in this study. The comparison with the results without damage in the chip clearly shows that similar trends are obtained for the forces which, in addition to the prediction of segmented chips morphologies, confirms the capacity of the model to correctly predict the trends and give relevant qualitative information. In accordance with previous works [4, 9, 13, 37], the results show that Ti6Al4V segmented chip formation is due to the strain softening and the propagation of a crack inside the primary shear zone.

Application to continuous chips formation

The main objective of the numerical model is to predict the trend of the results evolution when the cutting conditions vary. Up to now, only one uncut chip thickness has been considered, 280 µm, that lead to the formation of a segmented chip. The three other uncut chip thicknesses of the experiments (40 µm, 60 µm and 100 µm) gave continuous chips [13]; all the other cutting conditions (Table 2) are unchanged. The three experimental chips are shown in Fig. 11a to c at a magnification factor of 200. They consist of continuous chips with very small and irregular segments along their entire length. No cracks were observed at these uncut chip thicknesses. Again, the chips were not deformed during the unrolling preceding the embedding thanks to the small cutting length (10 mm), providing short and not rolled up chips. The characteristics of the finite element model are the same as in the previous paragraph: the Sima constitutive model is adopted with damage in the sacrificial layer and in the chip. Only the uncut chip thickness is modified to correspond to that of the experiments.

Fig. 11
figure 11

Experimental [13] a 100 µm, b 60 µm, c 40 µm and numerical chips (Sima model with damage in the chip) after 350 µs d 100 µm, e 60 µm, f 40 µm, temperature plots (in K)

Full size image

The three numerical chips (Fig. 11d to f) are continuous as in the experimental reference, showing the ability of the model to give accurate results for different cutting conditions. To quantitatively characterize the chip morphologies, their thickness, \(h^{\prime }\), could have been measured. However, due to the sacrificial layer in the numerical model, a significant amount of material is lost when the uncut chip thickness is small (about 10% at 100 µm, 17% at 60 µm and 25% at 40 µm) and it makes no sense to measure it for a quantitative comparison with the experiments. Small segments qualitatively close to the experiments are observed for an uncut chip thickness of 100 µm. The numerical chips at 60 µm and 40 µm do not have these small segments (likely due to a mesh size larger than these very small segments). They tend to roll up after a small length of cut, contrary to the experiments. Modeled chips less rigid than the experimental ones were already observed at the uncut chip thickness of 280 µm. Although crack propagation in the chip is enabled in the numerical model, no crack is noticed. This is consistent with the experimental observations and confirms that the finite element model is well suited for Ti6Al4V orthogonal cutting modeling in different cutting conditions leading to different chip morphologies.

The chip is continuous for the three uncut chip thicknesses and therefore the cutting force (Fig. 12) is nearly constant and present small oscillations, as expected. At the beginning of the cut, a peak in the cutting force is clearly observed for the modeling. Its magnitude decreases with the uncut chip thickness. Table 8 summarizes the average RMS values of the forces for each cutting condition. As expected, the lower the uncut chip thickness, the lower the level of the forces. As for the uncut chip thickness of 280 µm, the numerical RMS value is lower than the experimental reference. The difference is between 20% and 30%, which is accurate enough to predict evolution trends for different cutting conditions. This shows that these other cutting conditions are well handled by the model and confirms the choice of Sima constitutive model.

Fig. 12
figure 12

Comparison of the numerical cutting forces (Sima model with damage in the chip) with the experimental RMS values (the thickness of the experimental lines represents the standard deviation) at h = 100 µm, 60 µm and 40 µm, low-pass filter cutoff frequency at 10 kHz

Full size image
Table 8 Cutting forces (Sima model with damage in the chip) summary when the chips are continuous
Full size table

Conclusions

Four empirical constitutive models aimed for modeling of Ti6Al4V in machining operation were considered. This study showed that they had a strong influence on the chip formation and the magnitude of the cutting force. Significant differences in the JC parameters of the four constitutive models were highlighted. They lead to differences in the stress-strain evolutions and in the cutting forces. The absence of information on the material used for the parameters identification may be the reason: different metallurgical states will induce different material behaviors and then different constitutive model parameters. It is therefore recommended to specify this information in future research focusing on the identification of material models parameters. The absence of damage properties in the chip showed the specificities of each flow stress but they were not sufficient, in these cutting conditions, to form a segmented chip close to the experimental reference. It was shown that the strain softening and the crack propagation in the chip are necessary features to form a segmented chip with a morphology close to the experimental reference.

Although some differences were still noticed for the morphology, as well as for the cutting force, in the cutting conditions adopted in this paper, the Sima constitutive model lead to the closest results to the experiments. The difference in the cutting force with the experimental reference value is of 22%, while, for the chip morphology, it is less than 1% for the height of the segments, 25% for the undeformed segment length and 53% for the valley. The application of the same finite element model (Sima constitutive model with crack propagation in the chip) for other uncut chip thicknesses values confirmed that it was well suited to model Ti6Al4V orthogonal cutting. The numerical morphologies were close to the experimental tests and it is important to note that, although crack propagation is enabled, no crack is observed in the chips at these smaller uncut chip thicknesses. This is in accordance with the experiments and highlights the ability of the model to produce reliable chips morphologies. The cutting force was estimated with an average error of 25%.

These results show that the model is able to give good results even with changing cutting conditions and in particular that the chip morphology changes completely in accordance with the experiments, without any tuning of the model. The presented model with the Sima flow stress and damage in the chip is therefore able to predict different types of chip morphologies (segmented, continuous) and to give relevant quantitative information, such as the cutting force, for different cutting conditions.