Introduction

Over the past years, many attempts have been made to increase the formability and reduce the springback of lightweight alloys using novel forming technologies [1,2,3]. Among these, superplastic forming (SPF)-based techniques have found successful industrial applications [3].

In general, polycrystalline materials having an excellent uniaxial tensile elongation, in the range of more than 200%, are considered superplastic. Superplasticity is usually observed for very fine grain alloys (with just a few microns), low strain rates (less than 10−2 s−1), and at high temperatures (over half of the melting temperature). Commonly, any sheet forming process which satisfies the above conditions is considered as superplastic forming (SPF) [4]. In recent years, many attempts have been made to reduce the SPF time, mainly by increasing the strain rate. These efforts have led to the development of “fast” superplastic forming processes termed Quick Plastic Forming (QPF) or High Speed Blow Forming (HSBF) [5].

The development of reliable constitutive equations is a critical step for the accurate simulation of complex shapes via the SPF/QPF process. Such simulations, often done using Finite Element Method (FEM) codes, are efficient tools for evaluating the performance of the process, and reduce the trial and error time [6,7,8,9,10,11]. To that end, several physically-based or phenomenological models have been introduced for this purpose constructed from uniaxial tension tests at a constant temperature (i.e., under an isothermal condition).

In Table 1, some of the most commonly cited models have been summarized. Of note is the fact that these models are either too simple for capturing hardening, softening, and the damage behavior of superplastic materials or they are too complicated and need extensive experimentation to determine the proper material constants and parameters.

Table 1 Viscoplastic constitutive equations for superplastic metals
Full size table

In Table 1, all the viscoplastic models share similarity by taking into account the strain rate sensitivity index (m-value). In fact, at a constant forming temperature, it has been reported that the ductility of superplastic metals increases by increasing the m-value [4]. The m-value of a sheet metal can be measured via monotonic uniaxial tension tests at various strain rates or strain rate jump tests [21,22,23].

The strain rate sensitivity index (m-value) is defined as [22]:

$$ m=\frac{\partial \ln \left(\sigma \right)}{\partial \ln \left(\dot{\varepsilon}\right)} $$
(18)

Remarkably, in most of the above constitutive models, the strain rate sensitivity index (m-value) is often taken into account as a constant (i.e., an average m-value). Indeed, it has been shown that for superplastic metals, the instantaneous m-value, defined from Eq. 18 by differentiating ln(σ) against ln(\( \dot{\varepsilon} \)), is not constant, and changes with strain rate and strain [4, 22, 23].

In the present manuscript, the dependency of instantaneous m-value on strain rate as well as plastic strain will be investigated. Based on the experimental findings, a new phenomenological constitutive model is introduced, and the application of the new model for predicting the flow behavior of two reference materials will be discussed.

Experiments

Determination of m-value

The authors recently investigated the impact of different testing methods on the determination of the strain rate sensitivity index [23]. It was found that instantaneous m-values determined from true stress-plastic strain curves were more reliable, as compared to values based on the strain rate jump test or stress relaxation methods. Thus, in the present study, uniaxial tensile tests were conducted for strain rates of 0.001, 0.01 and 0.1 s−1. Samples were prepared according to the ASTM E2448 standard [24] from the rolling direction of an AA5083 alloy sheet with a thickness of 1.1 mm (see Fig. 1a). All the tests were repeated at least three times, and showed a maximum standard error of ±5%. The tests were conducted in an MTS 100-kN servo-hydraulic machine at 470 °C (according to high-speed blow forming practice). An MTS environmental heating chamber, model 651, was utilized to achieve the required temperature. In-house tensile grips designed for clamping the samples were used in the tests to accommodate the thermal expansion of the specimens during the heating cycle. During the tests, the temperature of the sample was monitored by two K-type thermocouples. For each test, the crosshead displacement and load cell data were recorded by a PC equipped with MTS software. Using a MATLAB® code, the crosshead displacement (CRH) was automatically converted to the logarithmic strain as:

$$ \varepsilon =\ln \left(1+\frac{CRH}{L_0}\right) $$
(19)

where L0 is the initial gauge length.

Fig. 1
figure 1

Uniaxial tension specimen, a before, b after the tensile test

Full size image

In this study, the strains determined from crosshead displacement were initially calibrated to minimize the impact of crosshead displacement errors. For this purpose, in a dummy test, a high temperature contact extensometer was utilized to record the real strains. In Fig. 2, the measured strain from the crosshead displacement is plotted against the recorded strain from the extensometer. As shown in this figure, the two measurements are correlated by a linear relationship, except at the early stage of test. The initial deviation from linearity is probably due to the slipping of the extensometer at the beginning of the test. It must be noted that because of the high elongation of the superplastic alloy, it was not possible to use a conventional mechanical extensometer for the entire duration of the test. Moreover, using a non-contact measurement (e.g., with a Digital Image Correlation (DIC) system) was not possible since the specimen and the grips were located inside the heating furnace to ensure temperature uniformity during the test. Finally, all tests were carried out according to ASTM E2448, thereby minimizing any possible testing errors [24]. As shown in Fig. 1b, this assumption was fairly reasonable, especially for the lower strain rate levels. However, at higher strain rates (0.1 s−1), a localized necking was observed near the failure area, which could be related to the influence of the strain rate on the operating deformation mechanism in superplastic metals. As has been reported by several authors [3−5], the controlling deformation mechanism changes from grain boundary sliding (GBS) to dislocation creep (DC) with increasing strain rate (i.e., with a preponderance of less uniform deformation).

Fig. 2
figure 2

The measured strain from the extensometer vs. the calculated strain from the crosshead displacement for the calibration test at 470 °C and at a strain rate of 10−3 s−1

Full size image

The true stress-plastic strain curves for the studied material are presented in Fig. 3. As expected, the mechanical behavior of AA5083 depends significantly on the applied strain rate at elevated temperatures. By increasing strain rate, the material flow stress increases, while the total elongation decreases.

Fig. 3
figure 3

True stress vs. plastic strain curves for the studied material at 470 °C

Full size image

In this study, the yield stresses were calculated from a 0.2% offset strain line. For this purpose, the Young’s modulus of 17 GPa, corresponding to 470°C, assessed from the test using a mechanical extensometer, was considered. Then, the plastic strains were calculated by subtracting the yield strain from the total strain.

The detailed procedure for assessing the instantaneous and average m-values from the true stress-plastic strain data are provided in a previous publication by the authors [23]. The average m-value is conventionally assessed from the slope of a linear fitting of the logarithms of true stress versus plastic strain rate. For the studied material, the average m-value equals 0.42. Alternatively, one could determine the instantaneous m-values by calculating the derivative of logarithm of true stress with respect to logarithm of plastic strain rate (see Eq. 18). In this study, the derivative operation was applied on the three sets of true stress vs. plastic strain data using the OriginLab® software. As shown in Fig. 4, the instantaneous m-value is not constant, and varies with both plastic strain and strain rate. For example, at the onset of plastic deformation, the instantaneous m-values for the strain rates of 0.001, 0.01 and 0.1 s−1 are 0.52, 0.42 and 0.3, respectively. Moreover, at a constant strain rate of 0.001 s−1, the instantaneous m-values are equal to 0.52, 0.40, 0.35 and 0.30, at plastic strain levels of 0, 0.2, 0.4, and 0.6, respectively. By increasing the plastic strain from zero to 0.6, the instantaneous m-value decreases by 41, 39 and 37% corresponding to strain rates of 0.001, 0.01 and 0.1 s−1, respectively. The above findings indicate that considering an average m-value is not an accurate description of material behavior during the SPF/QPF process.

Fig. 4
figure 4

The instantaneous m-value as a function of strain rate and plastic strain for the studied material

Full size image

Determination of cavity volume fraction

X-ray microtomography is often applied to measure the volume fraction of cavities for aluminum-magnesium superplastic alloys [25]. In the present study, a Nikon XT H 225 device was used for scanning the sheet coupons. To that end, six specimens were tensile-tested to different strain levels with a strain rate of 10−3 s−1 at 470 °C. Then, the deformed specimens were cut from the middle of the gauge length and glued together. Finally, the stack of test coupons was mounted on the X-ray holder.

In the test, the beam energy was 160 kV, with beam current of 25 μA, providing a voxel resolution of 6.1 μm. During the test, the samples rotated 180° around the tensile axis. The 2D projections of the X-ray were recorded by the detector as 1677 × 2000 pixel images. After the test, 2635 radiographs were processed by the VGStudio Max® V.2.2 software to reconstruct a 3D image of the samples and measure the volume fraction of the cavities for a volume of interest (see Fig. 5). In addition, from the 3D X-ray images, the final thickness (tf) and width (wf) of each volume of interest was determined. Subsequently, the three strain components (εl, εw, and εt) and equivalent plastic strains corresponding to each volume of interest were assessed from the following equations:

$$ {\varepsilon}_w=\ln \left(\frac{w_f}{w_0}\right) $$
(20)
$$ {\varepsilon}_t=\ln \left(\frac{t_f}{t_0}\right) $$
(21)
$$ {\varepsilon}_l=-\left({\varepsilon}_w+{\varepsilon}_t\right) $$
(22)
$$ {\overline{\varepsilon}}_p=\sqrt{\frac{2}{3}\left({\varepsilon_l}^2+{\varepsilon_w}^2+{\varepsilon_t}^2\right)} $$
(23)
Fig. 5
figure 5

3D image of the cavities for a volume of interest with an effective plastic strain level of 1.42

Full size image

With this approach, the equivalent plastic strain and volume fraction of cavities corresponding to each selected volume of interest was determined. As shown in Fig. 6, the volume fraction of the cavities increases exponentially with increasing plastic strain. A similar trend has been reported for a similar material in literature [25, 26].

Fig. 6
figure 6

Evolution of cavity volume with plastic strain

Full size image

The proposed model

Based on the observed dependency of instantaneous m-value on strain and strain rate (Fig. 4), Eq. 18 can be rewritten as:

$$ \frac{\partial \ln \left(\sigma \right)}{\partial \ln \left({\dot{\varepsilon}}_p\right)}=\mu \left({\varepsilon}_p,{\dot{\varepsilon}}_p\right) $$
(24)

where \( \mu \left({\varepsilon}_p,{\dot{\varepsilon}}_p\right) \) is any mathematical expression describing the dependency of instantaneous m-value on the plastic strain and strain rate. From this equation, the unit of μ is defined as [ln (MPa)/ln (s−1)]. In the present study, based on analyses of the obtained results, the following phenomenological equation is proposed for describing the function μ:

$$ \mu \left({\varepsilon}_p,{\dot{\varepsilon}}_p\right)=g\left({\varepsilon}_p\right)\mathit{\ln}\left({\dot{\varepsilon}}_p\right)+h\left({\varepsilon}_p\right)+{m}_0 $$
(25)

where m0 is a constant and g(εp)and h(εp)are functions of the plastic strain:

$$ g\left({\varepsilon}_p\right)={g}_1+{g}_2{\varepsilon}_p $$
(26)
$$ h\left({\varepsilon}_p\right)={h}_1{\left({\varepsilon}_p+{h}_2\right)}^{h_3}+{h}_4{\varepsilon}_p $$
(27)

where g1, g2, h1, h2, h3 and h4 are constants. In order to maintain the units’ consistency, m0, h1 and h4 are described in [ln (MPa)/ln (s−1)], g1 and g2 in [ln (MPa)/ln2 (s−1)], while h2 and h3 are dimensionless quantities.

By substituting Eq. 25 into Eq. 24, and by integrating this equation, the stress is defined by:

$$ \sigma =\mathit{\exp}\left(\frac{1}{2}g\left({\varepsilon}_p\right)l{n}^2\left({\dot{\varepsilon}}_p\right)+\left(h\left({\varepsilon}_p\right)+{m}_0\right)\ln \left({\dot{\varepsilon}}_p\right)+{m}_1\right) $$
(28)

Here, m1 is the integration constant described in [ln (MPa)]. Finally, in order to account for the evolution of cavitation during the SPF/QPF, in accordance with Eq. 17, the effective flow stress is given by:

$$ {\sigma}_{eff}\left({\varepsilon}_p,{\dot{\varepsilon}}_p,{f}_a\right)=\left(1-{f}_a\right)\sigma $$
(29)

Validation of the proposed model

Due to its simplicity, a family of power law (Norton-Hoff [12, 13]) equations (Eq. 1) has often been applied for modeling superplastic forming [7,8,10]. Therefore, the proposed model was applied to the studied material and compared with the power law model. As described earlier, the instantaneous m-values were calculated from the true stress-plastic strain curves of the studied material, and the cavitation parameters, f0 and φ, were obtained from the X-ray microtomography results (Fig. 6).

The other parameters of the proposed model (m0, m1, h1, h2, h3, h4, g1, and g2) were numerically calculated. For this calculation, a normalized least square error function (SN) was defined as follows for each strain rate:

$$ SN=\sum \frac{{\left({\sigma}_{\mathrm{exp}}-{\sigma}_{\mathrm{mod}}\right)}^2}{{\sigma^2}_{\mathrm{exp}}} $$
(30)

where σexp and σmod are the experimental and predicted true stress, respectively. Then, by minimizing the total error, i.e., the summation of the normalized errors corresponding to different strain rates (Err in Eq. 31), the constants were determined.

$$ Err=S{N}_{{\dot{\varepsilon}}_1}+S{N}_{{\dot{\varepsilon}}_2}+...+S{N}_{{\dot{\varepsilon}}_n} $$
(31)

In this study, using the SOLVER function in Microsoft Excel, the model parameters were iteratively changed to reach the least Err. The model parameters and corresponding total error (Err) for the studied material are listed in Table 2.

Table 2 Proposed model parameters for the studied material
Full size table

For the Norton-Hoff (power law) model, the average m-value at the start of plastic deformation was calculated. By best fitting of the true stress-plastic strain curve at a strain rate of 0.001 s−1, the material constants in Eq. 1, i.e., K and n, were assessed to be 240 MPa.sm and 0.21, respectively.

The uniaxial flow curves predicted by the new model and by the power law (Eq. 1) are compared with the experimental results in Fig. 7. While the new model could successfully show the hardening, softening and the damage behaviors of the studied material, the power law presents only a good prediction for the low strain rate (i.e. 10−3 s−1) corresponding to the conventional SPF process (SN is 2.8, 35, and 410 for strain rates of 10−3, 10−2 and 10−1 s−1, respectively). In fact, by increasing the strain rate from 10−3 to 10−2 and 10−1 s−1, the strain hardening term (Kεn) is multiplied by 2.6 and 6.9, respectively. Consequently, the power law fails to predict the flow behavior of the material at higher strain rates (above 10−2 s−1), corresponding to the “fast” superplastic forming processes.

Fig. 7
figure 7

Experimental and predicted true stress-plastic strain curves for the studied material

Full size image

If the damage term (fa) in Eq. 29 is set to zero, the model reduces to its simplest form, as described by Eq. 28. Overall, as shown in Fig. 8, the predicted true stress-plastic strain curve shows less discrepancy with the experimental results when the damage term is taken into account (Eq. 29) than when the latter is not considered. Yet, the proposed model in its simplest form (i.e., without considering damage) could satisfactorily predict the uniaxial flow behavior of the studied material with an Err value of about 2.81. In Fig. 9, the evolution of residuals (the difference between the experimental observation and the model prediction stresses) with plastic strain is presented for two versions of the new model (with and without considering the damage model). This figure confirms the previous argument, wherein at lower plastic strain levels, the residuals are near-zero, and almost identical for both versions of the new model. For the three strain rates, when the plastic strain is increased up to the failure strain, the residuals show more discrepancy between the predicted and observed stresses. In particular, the discrepancy is noticeable when the strain rate is equal to 10−1 s−1. These results could be attributed to experimental errors due to non-uniformity of deformation within the specimens at higher strain rates (see Fig. 1b). Moreover, in the present model, the damage term is likely too simple to consider the impact of strain rate variations.

Fig. 8
figure 8

Prediction of true stress-plastic strain curves using the new model with and without considering damage term

Full size image
Fig. 9
figure 9

Variation of residuals with plastic strain for two versions of the new model for strain rate of a 10−3 s−1, b 10−2 s−1, and c 10−1 s−1

Full size image

Next, further confirmation of the new model was obtained by comparing its performance with that of the simplified microstructure-based overstress (SMO) model (Eq. 15–17 in Table 1) [20], which has been frequently applied in the FE simulation of SPF/QPF of sheet metals [27,28,29,30,31]. To this end, the material data from Ref. [28] for AA5083 at 450 °C were considered, and the parameters of the new model were calibrated in the same fashion as was explained earlier. The new model parameters for this material are listed in Table 3.

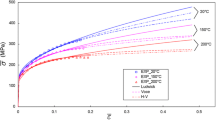
Table 3 Proposed model parameters for AA5083 (data from Jarrar et al. [28])
Full size table

As presented in Fig. 10, the experimental true stress-plastic strain curves (symbols) are presented, along with the predicted curves from the new model and from the simplified microstructure-based overstress model (i.e., Eqs. 15 to 17) used in Ref. [28]. A significant discrepancy between the two models is observed. While both hardening and softening of the material are well captured by the new model, the reference model (Eq. 15–17) could only give a rough estimation of the material behavior.

Fig. 10
figure 10

The true stress-plastic strain curves for AA5083 from Jarrar et al. [28] (symbols) predicted with the proposed model (solid lines) and the simplified microstructure-based overstress (SMO) model (dashed lines) at strain rates of a 0.0005, b 0.001, c 0.003, d 0.01, e 0.03 and f 0.1 s−1

Full size image

This discrepancy is presented in Fig. 11, where the residuals are plotted for the new and SMO models at six strain rates. In this figure, the local errors (residuals) corresponding to the proposed model are much fewer than those seen in the SMO model (Ref. [20]).

Fig. 11
figure 11

Residuals corresponding to the predictions in Fig. 9 for strain rates of a 0.0005, b 0.001, c 0.003, d 0.01, e 0.03 and f 0.1 s−1

Full size image

Thus, at both low and high strain rates, the new model provides a better prediction of the material flow behavior as compared to the two existing models. Specifically, as mentioned earlier, the m-value is considered as a constant in almost all models (e.g., power law and SMO model). Moreover, since in Eq. 15, p and C3 are strain rate-dependent (see Ref. 28), the determination of material parameters and constants will therefore not be accurate when considering a constant m-value.

Finally, for further verification of the new model, the predictions of the experimental results of an SPF magnesium alloy [31] were considered. In this case, the parameters of the new model were assessed from five out of nine true stress-plastic strain curves, corresponding to strain rates of 2 × 10−5, 10−4, 5 × 10−4, 2.5 × 10−3 and 10−2 s−1 (see Table 4). Then, the other four true stress-plastic strain curves were compared with the new model predictions (see Fig. 12a). As indicated, although the model parameters were calibrated from five sets of true stress-plastic strain curves, the model was able to predict the true stress-plastic strain curves for the four intermediate strain rates. In Fig. 12b, the local discrepancies between the experimental and predicted stresses are presented, and indicate that for a wide range of plastic strains, the residuals were nearly zero. At higher strain levels (near failure), the discrepancy between the model predictions and the experimental observations increases slightly.

Table 4 Proposed model parameters for AZ31 (Ref. [31] data)
Full size table
Fig. 12
figure 12

a Experimental (from Abu-Farha et al. [31]) and predicted flow curves of AZ31 for various strain rates, b variation of the residuals for various strain rates

Full size image

It can be seen that the proposed model satisfactorily predicts the most important features of the material flow behavior. For instance, for a wide range of strain rates, the proposed model captures the strain hardening behavior of each curve, corresponding to the range of initial to maximum stresses. Moreover, the softening and the damage behaviors of each curve, corresponding to the range of maximum stress to the stress at the end of the test, are fairly predicted for the entire range of strain rates.

Although the proposed model was established based on the definition of the strain rate sensitivity index, which has a physical meaning, it should still be considered as an empirical model, since no physical meaning has been associated with its parameters.

Nevertheless, it is important to note that the model requires minimum experimentation since all its parameters can be defined from a set of tensile tests (involving three strain rates). The calibration procedure for finding the parameters is straightforward, which eliminates the need for special mathematical software or coding. This could also significantly reduce the calculation cost as compared to more sophisticated models (e.g., unified constitutive model [17] and microstructure-based overstress equation [18, 19]).

Conclusions

Based on the variation of the m-value with a strain rate and plastic strain, a new model for predicting the uniaxial flow behavior of superplastic metals at different strain rates was proposed. The new model requires minimum experimentation and calculations for determination of the constants.

The new model was successfully applied for the prediction of strain hardening, softening and damage behaviors of three superplastic metals in uniaxial tension tests. Compared with the Norton-Hoff model (power law) and the simplified microstructure-based overstress model, the proposed model could predict material flow behavior more realistically.