Introduction to incremental sheet metal forming and its simulation

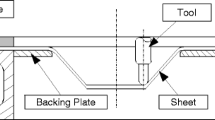
Incremental sheet forming (ISF) is a flexible forming process for small batch manufacturing and rapid prototyping of almost arbitrary 3D shapes. In ISF, a clamped sheet metal is formed progressively by a moving forming tool (Fig. 1, right). In contrast to conventional sheet metal forming processes such as deep drawing (Fig. 1, left), only a single die is needed, which does not have to be a full male or female die but can be a partial support.

Fig. 1
figure 1

Illustration of conventional deep drawing and ‘single point incremental forming’(SPIF)

Full size image

The tool path covers the surface of the desired product, similar to the finishing stage in z-level machining. In every instant of the forming process in which the tool moves over the sheet metal, localized plastic deformation is produced, and the final part shape is the result of all localized plastic deformation events. Various process variants of ISF have been developed with great effort by a number of research groups, but up to now only with limited industrial take-up. To make ISF viable in an industrial context, fast and reliable process simulations tools are needed. Process models should allow for the prediction of springback, the strain distribution, the forming forces, and the occurrence of failure. Such results would help investigate the feasibility of given part designs and allow for identifying suitable forming strategies off-line, before forming.

During the process, fast models are desired to build up on-line process control strategies, which would open the possibility to form a given part without excessive intervention of a human operator and expensive experimental trial-and-error trouble-shooting.

Up to now, ISF is far from being an easy-to-simulate process, and tools for virtual tryout that would allow for ‘first-time right’ production are not at hand. The main reason for the problems involved in the simulation of ISF are that the process is characterized by a small, moving plastic zone that is much smaller than the sheet metal blank. The high gradients in the plastic zone call for a fine discretization, but meshing the entire part with a fine mesh would leave tremendous potentials for time saving unexploited. Hence, adaptive re-meshing or domain decompositions methods are needed to track the deformation zone with a high resolution. Several attempts have been made to speed up implicit finite element (FE) simulations of ISF. A dedicated domain decomposition algorithm for the simulation of ISF was presented by Sebastiani et al. [1]. The approach separates the forming zone from the remaining sheet metal by introducing ‘springs’. This approach was later extended by Sebastiani et al. [2] to allow for 3D calculations using static condensation techniques. Similar work on was reported by Hadoush et al. [3] who developed a substructuring approach. Later, Hadoush et al. [4] also presented a substructuring/domain decomposition approach and adaptive mesh refinement (but no coarsening) for fast simulations of ISF. The acceleration factors reached were 2.4 in the first and 3.6 in the second case.

Even though the work cited above has shown that the calculation times can be reduced considerably, the simulation of industrial-size components may still result in unacceptably long computation times when implicit solvers are used. As shown by Bambach et al. [5], in implicit FE simulations, a considerable restriction on calculation time stems from the time step, which is bounded to relatively small values due to the ever changing contact situation. To reduce the CPU time, Dal Santo et al. [6] presented a method which mimics the deformation imposed by the moving tool by displacement boundary conditions and achieved a 65 % reduction in calculation time, but sacrificed the description of friction. Dedicated contact algorithms for incremental forming were also presented by Brunssen et al. [7] and by Henrard et al. [8].

In this paper, a fast model for ISF will be introduced and discussed. The approach detailed in the section “Fast explicit FE simulation of ISF through adaptivity and subcycling” embeds an adaptive re-meshing scheme with subcycling into dynamic explicit FEA of ISF to reduce the computing time of full-scale finite element solutions. The section “Performed Calculations” details the simulations that were performed to explore the approach. The results are presented in the section “Results and discussion”, and a discussion of the findings is given.

Fast explicit FE simulation of ISF through adaptivity and subcycling

Explicit FEA of ISF

Dynamic explicit FE models seem to be well-applicable to ISF due to their robust treatment of contact problems and material non-linearities. However, as typically done in explicit FE simulations of metal forming processes, the calculation has to be sped up by suitable scaling of process time or mass. Otherwise, the calculation times are unacceptably long.

This can be easily understood by analyzing how the CPU time of an explicit finite element model for ISF scales with the size of the part. A simple model for the CPU time of explicit FE simulations of ISF is obtained by assuming that the CPU time per element and increment t el,incr is a constant that depends on the speed of the computer. In this case, the number of increments can be computed by dividing the length of the tool path by the average tool velocity and the stable time increment size, and the total CPU time is:

$$ {T}_{CPU}=\frac{path\; length}{velocity\times stable\; incr.}\times number\; of\; element s\times CPU\; time\; per\; element\; and\; incr ement $$
(1)

A simple cone whose height matches its radius R shall be considered according to Fig. 2. It shall be formed with an average tool speed of v and a constant step down of d z . The CPU time can be written as:

Fig. 2
figure 2

Scaling of CPU time for an explicit FE simulation of incremental forming of a cone

Full size image
$$ {T}_{CPU}=\frac{\pi {R}^2/{d}_z}{v\times h/{c}_d}\times \frac{R^2}{h^2}\times {t}_{el,\; incr} $$
(2)

Here, it is assumed that the blank is square, has an area of R 2 and is entirely meshed with square elements of the same edge length h. c d denotes the speed of sound. The CPU time scales with R 4 in this case, which is visualized in Fig. 2. The simple model for CPU time shows that already for a part of moderate size of ~400 mm, the CPU time is in the range of days on a single processor computer (as of 2013).

Possibilities to accelerate the CPU time can be derived easily from Eq. (2):

  • One can increase the tool velocity or apply mass scaling to increase the stable time increment.

  • The computation can be parallelized.

  • The number of elements can be reduced by adaptive re-meshing and additionally, since this yields elements of different size, they can be integrated with different time steps using subcycling.

Speeding up explicit simulations by scaling of the velocity of the process or by mass scaling is common, but in ISF, explicit codes require special attention regarding the definition of the tool path, as shown by Bambach and Hirt [9]. If a displacement based description of the tool trajectory is used, e.g. by a list of tool positions over time, an explicit FE simulation will have to deal with jumps in the tool velocity and discontinuities in the acceleration. Such trajectories produce a large amount of kinetic energy in the model, affecting mainly those elements that are currently in contact with the forming tool. Bambach and Hirt [9] thus present enhancements to explicit FE simulations of ISF, which help reduce and control the simulation error.

Without further acceleration, however, even explicit methods are not sufficiently fast to deal with large-size ISF models. Parallelization may help reduce the CPU time tremendously, but relying only on parallel computing would leave the potentials of CPU time reductions by adaptivity unused.

In the following, it is analyzed to which extent explicit FE simulations of ISF can be sped up by adaptive re-meshing with a fine-sized mesh that always follows the forming tool. Since such an adaptive re-meshing strategy leads to different element sizes in the fine mesh encompassing the forming zone and the coarse mesh in the remainder of the part, the elements outside the forming zone can be integrated with a larger time step than the elements in the forming zone. Using different time steps for elements of different size in explicit FEA is referred to as subcycling, as introduced by Belytschko et al. [10].

Adaptive re-meshing and subcycling

Adaptivity in the context of finite elements usually either refers to adaptive mesh refinement, i.e., modification of an existing mesh, or adaptive re-meshing, i.e., the replacement of the existing mesh by a new one. Both methods are usually used in combination with error estimates or error indicators. In the first case, the three methods of h-, p- and r-adaptivity are feasible:

  • h-adaptivity refers to subdividing elements into smaller ones;

  • p-adaptivity is based on increasing the polynomial order of the shape functions;

  • r-adaptivity refers to relocating the mesh nodes according to gradients in the solution.

In metal forming, h-adaptivity is much more common than p- and r-adaptivity. In an incremental forming process such as ISF, adaptivity needs to take the cyclic nature of the process into account. The r-method does not seem to offer sufficient flexibility to make sure that a fine, preferably undistorted mesh follows the forming tool all the time. The p-method seems feasible, but it is rather unhandy and thus unusual to increase the polynomial degree in an explicit FE simulation. The h-method can be used to refine the mesh locally, but if the mesh is not coarsened when the tool moves on, the number of elements will rapidly increase.

Allowing for refinement and coarsening, however, leads to the question of storing the deformation history. A material point that is deformed by the forming tool will usually experience various deformation cycles. If a patch of fine elements is placed around the deformation zone and follows it throughout the simulation, the results are frequently transferred from the current mesh to the updated mesh configuration. Due to the large number of mappings, care must be taken that the frequent transfer of results does not affect the computation results due to inevitable interpolation errors. Especially stresses are prone to be affected due to the fact that they are C−1 continuous in typical forming simulations. If the deformation history is tracked only by mapping the results from configuration i to i + 1, results once computed with a high accuracy on the fine mesh will be interpolated on the coarse mesh, and the information obtained with better resolution is lost. In Hirt et al. [11] and Bambach et al. [12], a multi-mesh method is applied to open-die forging. To perform the actual FE calculation, a coarse mesh is used that incorporates a patch of elements with a fine mesh size. To store results with a high resolution (whenever possible), a fine background mesh is used.

Ramadan et al. [13] presented a multi-mesh method based on tetrahedral elements which can be applied to arbitrary incremental forming processes. The approach followed here is similar to the multi-mesh methods cited above but has two major differences. First, it is based on shell and not 3D elements. Second, it uses explicit FEA and exploits subcycling to further accelerate the computation beyond the reduction achieved by adaptivity.

As shown in Fig. 3, a patch of fine elements is used to mesh the deformation zone, while the rest of the sheet is meshed with larger elements. The fine element patch is created as a mesh template and then continually displaced along with the forming tool. A background mesh is used to store the results whenever the patch of small elements is displaced. The coarse mesh is fully contained in the background mesh i.e. each element of the coarse mesh comprises (in the case detailed here) 2 × 2 elements of the background mesh, except for a transition zone between the meshes. The local patch of fine elements corresponds to the fine background mesh locally, except for the boundary between the coarse and fine mesh, where a smooth transition without hanging nodes cannot be accomplished without adapting the element shape.

Fig. 3
figure 3

Concept for adaptive re-meshing in finite element simulation of ISF

Full size image

During the simulation, data has to be transferred from the actual simulation mesh i to the storage mesh and then to mesh i + 1. The storage mesh stores the displacement field u (relative to the initial state), the effective strain ε and the sheet thickness t. The stress state does not only change in the forming zone during the simulation. Also, stress waves are generated in the explicit FEA, which propagate through the mesh. The stress is hence not stored on the storage mesh but transferred directly from mesh i to i + 1.

The basic operations for data transfer (shown exemplarily for the displacement components) are:

  • transfer from mesh i to the storage mesh:

    $$ \begin{array}{c}\hfill 1.\kern1em \varDelta {u}^{(i)}={u}^{(i)}-{\tilde{u}}_{st}^{(i)}\hfill \\ {}2.\kern1em \varDelta {u}^{(i)}\to \varDelta {\tilde{u}}^{(i)}\hfill \\ {}3.{u}_{st}^{\left(i+1\right)}={u}_{st}^{(i)}+\varDelta {\tilde{u}}^{(i)}\hfill \end{array} $$

  • transfer from the storage mesh to mesh i + 1

    $$ {u}_{st}^{\left(i+1\right)}\to {\tilde{u}}_{st}^{\left(i+1\right)}\to {u}^{\left(i+1\right)} $$

These operations are performed separately for each displacement component. The transfer from the actual mesh i to the storage mesh is not performed by interpolating the values of calculated on mesh i on the nodes of the storage mesh since such a procedure was shown to produce inaccuracies [11]. Instead, three steps are performed: In a first step, the difference ∆u (i) between the displacement field u (i) and the interpolated data that was used to transfer data from the storage mesh to mesh i (u st (i)) is calculated. This difference represents the changes to the data in the storage mesh that have been generated while mesh i has been active. In a second step, this field is interpolated on the nodes of the storage mesh, which yields Δũ (i). The interpolated values are used to update the storage mesh (step 3) by the increments that have been generated on mesh i.

To map the data from the storage mesh to mesh i + 1, an interpolant of the field present in the storage mesh is generated and this interpolant is evaluated at the nodes of mesh i + 1. Since the sheet metal occupies a domain with a fixed outer boundary, all interpolation steps are accomplished using scattered data interpolation techniques. Radial basis function are used to create a smooth interpolant from nodal data values. The interpolant reads to a given field variable X(x,y) reads

$$ \tilde{X}\left(x,y\right)={\displaystyle \sum_{i=1}^N{a}_i{\phi}_i(r);\;r={\left({\left(x-{x}_i\right)}^2+{\left(y-{y}_i\right)}^2\right)}^{1/2}} $$
(3)

with the W2-Wendland polynomial

$$ {\phi}_i(r)=\left(1+4r\right){\left(1-r\right)}_{+}^4 $$
(4)

The choice of the interpolation method is based on past experience with these methods and the development of fast solution procedures described in [14], which allow for an efficient computation of the interpolants.

To further reduce the calculation times, subcycling is applied so that the coarse elements are integrated with a larger time step than the fine elements in the deformation zone, i.e.

$$ \varDelta t\left({\varOmega}_1\right)=n\times \varDelta t\left({\varOmega}_1\right) $$
(5)

Performed calculations

To analyze the properties of the adaptive re-meshing approach with subcycling, a simplified ISF process using a helical tool path as shown in Fig. 4 is simulated. The model uses a blank of 200 × 200 mm size, S4R elements with h = 4 mm edge length in the coarse region and h = 2 mm in the finely discretized patch, the von Mises yield criterion with isotropic hardening, and a forming tool with 15 mm radius.

Fig. 4
figure 4

Illustration of the tool path and the adaptive re-meshing approach with a patch of fine elements following the forming tool. εeq is the equivalent plastic strain

Full size image

The helical tool path moves down into the sheet by 3 mm per revolution and contains 5 cycles. Hence, the forming depth is 15 mm at the end of the simulation. The helical tool path allows for a smooth definition of tool velocity and acceleration, so that artifacts created by jerky tool motion are avoided.

As material data for the sheet metal, mild steel with a Young’s modulus of 210GPa, a Poisson ratio of 0.3 and a Swift hardening law σ = 481.6(ε − 0.004)0.2 [MPa] was used. The purpose at this stage of development of the methodology is to analyze how re-meshing and subcycling affect the model predictions. For this purpose, a comparison with a full-scale reference model with a sufficiently fine mesh and no adaptivity and subcycling is sufficient. If the simulations reliably reproduce the reference simulation, they can be enhanced by more sophisticated material models and tested against experimental data.

Six simulations were performed: a reference simulation with a mesh size of 2 mm globally, a simulation with adaptive re-meshing and no subcycling, and 4 simulations with adaptive re-meshing and subcycling factors of 2, 3, 4 and 10, i.e. the ratio of the time step in the coarse region to that in the finely discretized patch corresponds to these factors. The results of the simulations using adaptive re-meshing and subcycling are compared to the reference solution with respect to calculation times and accuracy of Mises stress and equivalent strain.

Results and discussion

Table 1 shows the gain in calculation time of the simulation with the adaptive re-meshing approach and various subcycling factors compared to the reference solution with a globally fine mesh size of h = 2 mm. Adaptive re-meshing alone reduces the CPU time to ~28.8 % of the time needed with the globally fine mesh. Subcycling further reduces the CPU time to 24.8 % for a subcycling factor of 2, and to 12 % for a factor of 10.

Table 1 Gain in CPU time relative to a simulation with h = 2 mm everywhere and errors in Mises stress and strain. (ARM—adaptive re-meshing)
Full size table

Figure 5 shows a comparison of the von Mises stress and equivalent strain computed with the adaptive re-meshing method and various subcycling factors with the reference simulation, which uses a fine mesh (h = 2 mm) globally. Table 1 details the maximum errors in the von Mises stress and equivalent strain for all cases, which are computed as relative errors between the reference (σ ref Mises ) and the simulations with subcycling (σ sub Mises ), which yields

Fig. 5
figure 5

Relative error in the von Mises stress and the equivalent strain compared to the reference solution for simulations with adaptive re-meshing and various subcycling (SC) factors

Full size image
$$ rel.\; error=\left|\frac{\sigma_{Mises}^{ref}-{\sigma}_{Mises}^{sub}}{\sigma_{Mises}^{ref}}\right| $$
(6)

The relative error in Mises stress grows faster than the error in equivalent strain. Subcycling with a factor of 2–3 yields deviations in the von Mises stress and equivalent strain of ~10 % at most. It allows for acceleration factors of up to five, while maintaining sufficient accuracy, at least in the cases considered here.

At larger subcycling factors, the error in Mises stress exceeds 10 % (subcycling factor = 4) and reaches 25 % for a very large factor of 10. A subcycling ratio of 10 yields an acceleration by a factor 8.3 in combination with adaptive re-meshing, but the stress results are poor.

Interestingly, however, the error is much smaller in the deformation zone (~10 % at most) than in places in which no or hardly any plastic deformation occurs, so that even this subcycling factor may be used. The relative error in the undeformed portions appears large due to the fact that the overall stress level is low there, so that local variations of the stress state due to wave propagation leads to larger relative changes than in the deformation zone.

It can be stated here that explicit FEA with adaptive re-meshing and subcycling has the potential to achieve large savings in CPU time. Even in the relatively simple example considered here, in which the finely discretized deformation zone amounts for ~7.8 % of the area of the blank, savings of up to 80 % (subcycling factor 3) seem possible with sufficient accuracy.

The speed-up of the simulation refers only to a simulation of the truncated cone with given size. For larger industrial parts, the deformation zone may be much smaller in relation to the sheet metal, so that even larger reductions in CPU time may be achieved. It is hence interesting to analyze how the computation time scales with the size of the part, as done for the conventional explicit simulation in Fig. 2.

Figure 6 compares the reference simulation, for which the CPU time scales by a factor of 16 when the part size is doubled, with the scaling of CPU time when adaptive re-meshing is used alone or in combination with subcycling.

Fig. 6
figure 6

Scaling of CPU time with part size for conventional explicit FEA, adaptive re-meshing and adaptive re-meshing with subcycling

Full size image

Adaptive re-meshing reduces the scaling factor from 16 to 8.9 for the cone, due to the fact that the number of fine elements in the deformation zone is independent of part size and only the number of coarse elements scales with part size. Subcycling helps to further reduce the factor to ~5.6 when the part size is doubled. Both approaches together produce a much smaller slope in the dependence of CPU time on part size, allowing for much larger parts.

A problem that has not been given much attention so far is the stability of adaptive re-meshing for longer tool paths. Problems may arise from the frequent data mapping which may cause accumulation of interpolation errors. Future work will hence focus on issues related to robustness and stability of adaptive re-meshing in ISF.

Also, it may not be possible to use a fine mesh only in the primary deformation zone, since plastic deformation may also occur in other region such as the outer edges of the part, so that the adaptivity needs to take into account the spatial distribution of plastic deformation.

Conclusions and outlook

In this work, adaptive re-meshing and subcycling were combined to reduce the computational effort needed to simulate incremental sheet forming processes. The combined use of both methods allows for tremendous reductions in CPU time. Error control is still an unsolved issue in explicit simulations of incremental sheet forming which use a very large number of time steps, such that currently care must be taken with respect to the smoothness of the tool motion.