Secure communication via an energy-harvesting untrusted relay with imperfect CSI

Abstract

This paper studies the secure communication of an energy-harvesting system in which a source communicates with a destination via an amplify-and-forward (AF) untrusted relay. The relay uses the power-splitting policy to harvest energy from wireless signals. The source is equipped with multiple antennas and uses transmit antenna selection (TAS) and maximum ratio transmission (MRT) to enhance the harvested energy at the relay; for performance comparison, random antenna selection (RAS) is examined. The relay and destination are single-antenna nodes. To create a positive secrecy capacity, destination-assisted jamming is deployed. Because the use of multiple antennas can cause the imperfect channel state information (CSI), the channel between the source and the relay is examined in two cases: perfect CSI and imperfect CSI. To evaluate the secrecy performance, analytical expressions for the secrecy outage probability (SOP) and the average secrecy capacity (ASC) for the TAS, MRT, and RAS schemes are derived. Moreover, a high-power approximation for the SOP is presented. The accuracy of the analytical results is verified by Monte Carlo simulations. The results show the benefit of using multiple antennas in improving the secrecy performance. Specifically, MRT performs better than TAS, and both of them outperform RAS. Moreover, the results provide valuable insight into the effects of various system parameters, such as the channel correlation coefficient, energy-harvesting efficiency, secrecy rate threshold, power-splitting ratio, transmit powers, and locations of the relay, on the secrecy performance.

1 Introduction

Wireless energy harvesting (WEH) has considered as a potential technology for prolonging the lifetime of wireless networks in which wireless energy-constrained nodes power their batteries by scavenging energy from ambient radio frequency (RF) signals; hence, much costly and inconvenient of frequent battery replacement and recharging can be reduced [1, 2]. Since the RF signals can carry information as well as energy at the same time, an appealing new research direction of WEH known as “simultaneous wireless information and power transfer” (SWIPT) has recently emerged [3]. To realize the idea of SWIPT, the author of [3] designed two practical receiver architectures, namely, time switching (TS), where each processing block time is separated for harvesting energy and decoding information, and power splitting (PS), where the received signal strength is split into two streams, one for energy harvesting and the other for information decoding.

In [4], SWIPT was implemented in a cooperative communication strategy in which an energy-harvesting (EH) relay collects energy from a source and helps the source to send information to a destination. Work related to SWIPT with multiple cooperative relays was reported in [5]. In [6], the author considered a full duplex relaying SWIPT system where an EH relay collects energy from its two antennas and operates in full duplex mode to assist the communication between a source and a destination. In the presence of co-channel interference (CCI), the author of [7] studied the effect of CCI on a SWIPT system with a single-antenna EH relay; the extension of [7] to a scenario with a multiple-antenna EH relay was studied in [8]. It was shown in [7, 8] that the CCI could be exploited as a potential energy source. More recently, security in SWIPT has become a focus of research. The authors of [9] studied the effects of artificial noise (AN) and beamforming on the secure transmission of a multiple-input-single-output (MISO) SWIPT system containing a single information receiver (IR) and multiple energy receivers (ERs) which are capable of overhearing the information of IR. The similar work as in [9] for a scenario containing multiple IRs was presented in [10] in which each IR is not only decoding its information but also overhearing the information of the other IRs. For a case in which the relay is considered as a potential eavesdropper (i.e., an untrusted node), the authors of [11] showed that destination-assisted jamming could be effectively exploited to enhance the secrecy performance of an untrusted relaying SWIPT.

Most studies in SWIPT were conducted under the assumption that perfect channel state information (CSI) is available. However, in practical systems, the assumption of perfect CSI is not always valid due to the presence of feedback delay and channel estimation errors. Specifically, for the multiple-antenna systems, an exceedingly large amount of training/feedback overhead in the CSI acquisition causes high feedback delay which leads to the inaccurate CSI. For that reason, imperfect CSI is commonly assumed in the case of employing multiple-antenna techniques, such as transmit antenna selection (TAS) and maximum ratio transmission (MRT) at the transmitter, and selection combining (SC) and maximal ratio combining (MRC) at the receiver [12, 14]. This is because the increase in the number of antenna lead to the significant increase in the CSI acquisition. To the best of our knowledge, there have been no such works in literature to investigate the effect of an imperfect CSI on the secrecy performance of untrusted relaying SWIPT systems.

In this paper, we investigate the secure communication of a SWIPT system in which a multiple-antenna source communicates with a single-antenna destination via an amplify-and-forward (AF) untrusted EH relay. Two multiple-antenna schemes, TAS and MRT, are employed at the source to exploit the benefit of using multiple antennas; moreover, a random antenna selection (RAS) scheme is considered at the source for performance comparison. Although the use of multiple antennas improves the secrecy performance, it can cause the imperfect CSI. Thus, the CSI of the source-to-relay link is examined in two cases: perfect CSI and imperfect CSI whereas the CSI of the relay-to-destination link is assumed to be perfect. To create positive secrecy capacity, a destination-assisted jamming signal that is completely cancelled at the destination is adopted. Moreover, the jamming signal is also exploited as an additional energy source. The power-splitting (PS) receiver architecture is adopted. The secrecy performance is evaluated by analyzing the secrecy outage probability (SOP) and average secrecy capacity (ASC). To accomplish this, we derive the SOP expressions involving a single integral and a tight closed-form upper bound for the ASC. Moreover, closed-form expressions for the SOP at high power levels are also derived. The accuracy of the analytical results is verified by Monte Carlo simulations. Numerical results provide valuable insight into the effects of various system parameters, such as the correlation coefficient between the perfect CSI and imperfect CSI, the energy-harvesting efficiency, the transmit powers, the secrecy rate threshold, the power-splitting ratio, and the locations of the relay, on the secrecy performance.

Notation: |⋅| is the absolute value operator; ∥⋅∥ is the Frobenius norm; [⋅]^⊤ is the transpose operator; [⋅]^‡ is the Hermitian transpose operator; $\mathcal {C}\mathcal {N}(0,{\Omega })$ is a complex Gaussian distribution with zero mean and variance Ω; $\mathbb {E}\{\cdot \}$ is the expectation of a random variable; [x]⁺ = max{x,0}; K _υ (⋅) is the υ th order modified Bessel function [15, Eq. (8.407.1)]; E i(⋅) is the exponential integral function [15, Eq. (8.310.1)]; ψ(x) is the Digamma function [15, Eq. (8.360.1)]; Γ(⋅) is the gamma function [15, Eq. (8.310.1)]; Γ(α,x) the lower and upper incomplete gamma functions [15, Eq. (8.350.2)]; and U(a,b;x) is the confluent hypergeometric function of the second kind [15, Eq. (9.211.4)].

2 System model

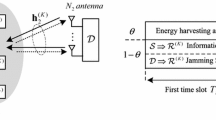
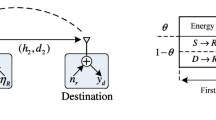
We consider the secure communication of an energy-harvesting system illustrated in Fig. 1a in which a source S is equipped with N antennas whereas an untrusted relay R and a destination D are single-antenna nodes. R uses the PS policy shown in Fig. 1b to harvest energy and uses the AF protocol to forward the source’s signal. In each block time T, the entire communication consists of two time slots, T/2. During the first time slot, R harvests energy and decodes information with a power-splitting ratio 0 < 𝜃 < 1 [4]. Then, R uses all harvested energy to forward the received signal to D during the second time slot. Throughout this paper, we assume that (1) no direct link between S and D exists, (2) the channels follow independent and identical Rayleigh distributions, hence, the channel gains are exponential random variables (RVs), (3) the CSI of the S → R link is examined in two cases: perfect CSI and imperfect CSI (because of using N antennas at S), whereas the CSI of the R → D link is perfect, and (4) a local CSI is required at S and R, and the full CSI and the value of transmit power at R are assumed to be available at D. The full CSI at D is a necessary condition to successfully decode the source signal. This is because the received signal at D in the AF protocol contains both the S → R and R → D CSI [13]. When D does not attain the S → R CSI, D is not capable of decoding the source signal. Moreover, because the S → R CSI can be imperfect, R sends the value of its transmit power to D for decoding the source signal optimally.

Fig. 1

System model

We denote h ₁ = [h _1,1,…,h _1,N ] as the channel vector between S and R during the channel estimation and feedback process. The elements of h ₁ follow identically and independently distributed (i.i.d.) $\mathcal {C}\mathcal {N}(0,\lambda _{1}^{-1})$ where $\lambda _{1} = d_{1}^{\tau }$, d ₁ is the normalized distance between S and R, and τ is the path loss exponent. We denote $\tilde {\textbf {h}}_{1}$ as the time-delayed version of h ₁. Mathematically, $\tilde {\textbf {h}}_{1}$ can be modeled as

$$ \tilde{\textbf{h}}_{1} = \sqrt{\zeta\textbf{h}_{1}} + \sqrt {1-\zeta} \textbf{e}, $$

(1)

where ζ ∈ [0,1] is the channel correlation coefficient, and e is an error vector in which the elements of e are i.i.d. $\mathcal {C}\mathcal {N}(0,\lambda _{1}^{-1})$. We also denote $h_{2}\sim \mathcal {C}\mathcal {N}(0,\lambda _{2}^{-1})$ as the channel between R and D where $\lambda _{2}=d_{2}^{\tau }$ and d ₂ is the normalized distance between R and D.

We investigate two transmit antenna schemes, TAS and MRT. In addition, a random antenna selection (RAS) scheme is also considered for performance comparison. In the RAS scheme, S randomly chooses an antenna to transmit its signal x _s , whereas, in the TAS scheme, S selects the best antenna (denote as the n ^∗-th antenna) to transmit x _s , which satisfies the condition given in Eq. 2.

$$ n^{*} = \underset{1\leqslant n\leqslant N}{\arg \max} \left\{{{\left| {{h_{1,n}}} \right|}^{2}} \right\}. $$

(2)

In the MRT scheme, S calculates a weight vector $\textbf {w}=\frac {\textbf {h}^{\dagger }}{\|\textbf {h}\|}$ and applies w to x _s before transmitting x _s on N antennas in the data transmission phase.

2.1 Communication in the first time slot

The received signal at R for three transmit antenna schemes in the first time slot is given by

$$ {y_{r}}\,=\,\left\{\begin{array}{llll} {{{\tilde h}_{1,ran}}\sqrt {\left( {1 - \theta} \right){P_{s}}} {x_{s}} + {h_{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}} {x_{d}} + {n_{r}}} &{\text{;}\,\left( {\text{RAS}} \right)} \\ {{\tilde{h}_{1,n*}}\sqrt {\left( {1 - \theta} \right){P_{s}}} {x_{s}} + {h_{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}} {x_{d}} + {n_{r}}} &{\text{;}\,\left( {\text{TAS}} \right)} \\ {\tilde{\mathbf{h}}_{1}{\mathbf{w}_{1}}\sqrt {\left( {1 - \theta} \right){P_{s}}} {x_{s}} + {h_{2}}\sqrt {\left( {1 -\theta} \right){P_{d}}} {x_{d}} + {n_{r}}} &{\text{;}\,\left( {\text{MRT}} \right)} \end{array}\right., $$

(3)

where P _s and P _d are the transmit powers of S and D, respectively, x _d is the AN of D, and $n_{r}\sim \mathcal {C}\mathcal {N}(0,{\sigma _{0}^{2}})$ is the additive white Gaussian noise (AWGN) at R. Using Eq. 1, we can rewrite Eq. 3 as

$$ {y_{r}} \,=\,\! \left\{\begin{array}{lll} {h_{1,ran}}\sqrt {\zeta \left( {1 - \theta} \right){P_{s}}} {x_{s}} + e\sqrt {\left( {1 - \zeta} \right)\left( {1 - \theta} \right){P_{s}}} {x_{s}} \\ \qquad + {h_{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}} {x_{d}} + {n_{r}} &{\text{;}\,\left( {\text{RAS}} \right)} \\ {h_{1,n*}}\sqrt {\zeta \left( {1 - \theta} \right){P_{s}}} {x_{s}} + e\sqrt {\left( {1 - \zeta} \right)\left( {1 - \theta} \right){P_{s}}} {x_{s}} \\ \qquad + {h_{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}} {x_{d}} + {n_{r}} &{\text{;}\,\left( {\text{TAS}} \right)} \\ {\mathbf{h}_{1}}{\mathbf{w}_{1}}\sqrt {\zeta \left( {1 - \theta} \right){P_{s}}} {x_{s}} + \mathbf{e}{\mathbf{w}_{1}}\sqrt {\left( {1 - \zeta} \right)\left( {1 - \theta} \right){P_{s}}} {x_{s}} \\ \qquad + {h_{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}} {x_{d}} + {n_{r}} &{\text{;}\,\left( {\text{MRT}} \right)} \end{array}\right.. $$

(4)

For notational convenience, we define X ₁ and $\tilde {X}_{1}$ as follows.

$$ X_{1} \,=\, \left\{\begin{array}{lll} |h_{\textup{1,ran}}|^{2} &{\text{;}\,\left( {\text{RAS}} \right)} \\ |h_{1,n^{*}}|^{2} &{\text{;}\,\left( {\text{TAS}} \right)} \\ \|\mathbf{h}_{1}\mathbf{w}_{1}\|^{2} &{\text{;}\,\left( {\text{MRT}} \right)} \end{array}\right., \text{ and } \tilde{X}_{1} = \left\{\begin{array}{lll} |\tilde{h}_{\textup{1,ran}}|^{2} &{\text{;}\,\left( {\text{RAS}} \right)} \\ |\tilde{h}_{1,n^{*}}|^{2} &{\text{;}\,\left( {\text{TAS}} \right)} \\ \|\tilde{\mathbf{h}}_{1}\mathbf{w}_{1}\|^{2} &{\text{;}\,\left( {\text{MRT}} \right)} \end{array}\right.. $$

(5)

Then, the harvested energy at R is calculated as

$$ {E_{h}} = \eta \theta Y T/2, $$

(6)

where η is the RF-to-DC conversion efficiency, $Y=P_{s}\tilde {X}_{1} + P_{d} X_{2}$ and X ₂ = |h ₂|².

From Eq. 4, the signal-to-interference-and-noise ratio (SINR) at R can be expressed as

$$ \gamma_{r}=\frac{\zeta(1-\theta)\rho_{s} X_{1}}{(1-\theta)\rho_{d} X_{2} +\mu}, $$

(7)

where $\rho _{s}=P_{s}/{\sigma _{0}^{2}},\rho _{d}=P_{d}/{\sigma _{0}^{2}}$, and $\mu =(1-\zeta )(1-\theta )\frac {\rho _{s}}{\lambda _{1}}+1$.

2.2 Communication in the second time slot

In the second time slot, R uses all harvested energy in Eq. 6 to forward its received signal; therefore, the transmit power of R is P _r = 2E _h /T = η 𝜃 Y. The received signal at D is given by

$$ {y_{d}} = \sqrt {{P_{r}}} {h_{2}}G{y_{r}} + {n_{d}}, $$

(8)

where $G=1/\sqrt {\kappa P_{r}+{\sigma _{0}^{2}}}$ with κ = (1 − 𝜃)/η 𝜃. Substituting Eqs. 4 into 8 yields

$$ y_{d} \,=\, \left\{\begin{array}{lllll} \!\underbrace {{h_{1,ran}}{h_{2}}\sqrt {\zeta \left( {1 - \theta} \right){P_{s}}{P_{r}}} G{x_{s}}}_{desired\,signal} + \underbrace {{h_{2}^{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}{P_{r}}} G{x_{d}}}_{AN} \\ \qquad \!+ \underbrace {e{h_{2}}\sqrt {\left( {1 - \zeta} \right)\left( {1 - \theta} \right){P_{s}}{P_{r}}} G{x_{s}} + {h_{2}}\sqrt {{P_{r}}} G{n_{r}} + {n_{d}}}_{overall\,noise} &{\text{{};}\,\left( {\text{RAS}} \right)} \\ \!\underbrace {{h_{1,n*}}{h_{2}}\sqrt {\zeta \left( {1 - \theta} \right){P_{s}}{P_{r}}} G{x_{s}}}_{desired\,signal} + \underbrace {{h_{2}^{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}{P_{r}}} G{x_{d}}}_{AN} \\ \qquad \!+ \underbrace {e{h_{2}}\sqrt {\left( {1 - \zeta} \right)\left( {1 - \theta} \right){P_{s}}{P_{r}}} G{x_{s}} + {h_{2}}\sqrt {{P_{r}}} G{n_{r}} + {n_{d}}}_{overall\,noise} &{\text{{};}\,\left( {\text{TAS}} \right)} \\ \!\underbrace {{\mathbf{h}_{1}}{\mathbf{w}_{1}}{h_{2}}\sqrt {\zeta \left( {1 - \theta} \right){P_{s}}{P_{r}}} G{x_{s}}}_{desired\,signal} + \underbrace {{h_{2}^{2}}\sqrt {\left( {1 - \theta} \right){P_{d}}{P_{r}}} G{x_{d}}}_{AN}\\ \qquad \!+ \underbrace {\mathbf{e}{\mathbf{w}_{1}}{h_{2}}\sqrt {\left( {1 - \zeta} \right)\left( {1 - \theta} \right){P_{s}}{P_{r}}} G{x_{s}} + {h_{2}}\sqrt {{P_{r}}} G{n_{r}} + {n_{d}}}_{overall\,noise} &{\text{;}\,\left( {\text{MRT}} \right)} \end{array}\right.{}. $$

(9)

Because D can eliminate the AN in Eq. 9 and $\mathbb {E}\{\mathbf {ew}_{1}\left (\mathbf {ew}\right )^{*}\}=\lambda _{1}^{-1}$, the end-to-end signal-to-noise (SNR) at D is calculated as

$$ \gamma_{d} = \frac{{\zeta \left( {1 - \theta} \right){\rho_{s}}{X_{1}}{X_{2}}{P_{r}}}}{{{P_{r}}\left( {{X_{2}}\mu + \kappa} \right) + {\sigma_{0}^{2}}}} \approx \frac{{\zeta \left( {1 - \theta} \right){\rho_{s}}{X_{1}}{X_{2}}}}{{{X_{2}}\mu + \kappa}}. $$

(10)

The approximation in Eq. 10 is acceptable because the noise variance term is negligible compared to the other factors in the denominator.

3 Performance analysis

3.1 The outage probability

According to [16], the instantaneous secrecy rate of the proposed system is calculated as

$$ {R_{\sec}} = {\left[ {{\mathcal{C}_{\text{d}}} - {\mathcal{C}_{\text{r}}}} \right]^ +} , $$

(11)

where ${\mathcal {C}_{d}} = {\log _{2}}\left ({1 + {\gamma _{d}}} \right )$, and ${\mathcal {C}_{r}} = {\log _{2}}\left ({1 + {\gamma _{r}}} \right )$. Then, the SOP is given by

$$\begin{array}{@{}rcl@{}} \text{SOP} &\,=\,& \Pr \left( {{R_{\sec} } \!<\! {R_{{\text{th}}}}} \right) \\ &\,=\,& \Pr \left( {\zeta \left( {1 \,-\, \theta} \right){\rho_{s}}{X_{1}}{\Xi} \left( {{X_{2}};\beta} \right) \!<\! \beta \,-\, 1} \right) \\ &\,=\,& 1 \,-\, \Pr \left( {{X_{1}} \!>\! \frac{{\beta \,-\, 1}}{{\zeta \left( {1 - \theta} \right){\rho_{s}}{\Xi} \left( {{X_{2}};\beta} \right)}}|{X_{2}} \!>\! {{\bar x}_{1}}} \right),\\ \end{array} $$

(12)

where $\beta =2^{R_{th}}$, ${\Xi } \left ({x;\beta } \right ) = \frac {x}{{\mu x + \kappa } } - \frac {\beta } {{x\left ({1 - \theta } \right ){\rho _{d}} + \mu } }$, and ${\bar x_{1}} = \frac {{\mu \left ({\beta - 1} \right ) + \sqrt {{\mu ^{2}}{{\left ({\beta - 1} \right )}^{2}} + 4\beta \left ({1 - \theta } \right ){\rho _{d}}\kappa } } }{{2\left ({1 - \theta } \right ){\rho _{d}}}}$ is the positive root of the equation Ξ(x;β) = 0.

Proposition 1

The SOP of the RAS, TAS, and MRT schemes can be expressed as

$$\begin{array}{@{}rcl@{}} \text{SOP}_{\text{RAS}} \!&=&\! 1 - {\lambda_{2}}\int\limits_{{{\bar x}_{1}}}^{+ \infty} {{e^{- \frac{\alpha} {{\Xi \left( {x;\beta} \right)}} - {\lambda_{2}}x}}} dx, \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} \text{SOP}_{\text{TAS}} \!&=&\! 1 \,+\, {\lambda_{2}}\sum\limits_{n = 1}^{N} \binom{N}{n} {\left( { - 1} \right)^{n}}\int\limits_{{{\bar x}_{1}}}^{+ \infty} {{e^{- \frac{{n\alpha} }{{\Xi \left( {x;\beta} \right)}} - {\lambda_{2}}x}}} dx, \end{array} $$

(14)

$$\begin{array}{@{}rcl@{}} \text{SOP}_{\text{MRT}} &=& 1 - {\lambda_{2}}\sum\limits_{n = 0}^{N - 1} \frac{{{\alpha^{n}}}}{{n!}} \int\limits_{{{\bar x}_{1}}}^{\infty} {\Xi {{\left( {x;\beta} \right)}^{- n}}} {e^{- \frac{\alpha} {{\Xi \left( {x;\beta} \right)}} - {\lambda_{2}}x}}dx,\\ \end{array} $$

(15)

where $\alpha = \frac {\lambda _{1}\left (\beta - 1 \right )}{\zeta \left (1 - \theta \right )\rho _{s}}$ .

Proof

See Appendix A. □

In the case of perfect CSI (ζ = 1), Eq. 13 identically matches with [11, Eq. (15)]. This is because the increase in N in the RAS scheme does not influence the system performance. For that reason, the secrecy performance of the RAS scheme for the case N > 1 is equal to that for the case N = 1 (when N = 1 and ζ = 1, our proposed system is the same with the proposed system of [11]). Similarly, in the case of N = 1 and ζ = 1, Eqs. 14 and 15 reduce to the same expression with [11, Eq. (15)].

To the best of our knowledge, the integrals in Eqs. 13–15 do not admit closed-form expressions. Below, we derive the asymptotic functions for the SOP at high power levels, i.e., (P _s ,P _d ) → (∞,∞).

Proposition 2

In the case of perfect CSI ( ζ = 1), the asymptotic functions for the SOP of the RAS, TAS, and MRT schemes are given by

$$ \text{SOP}_{\text{RAS}}^{\infty} = \text{SOP}_{\text{TAS}}^{\infty} = \text{SOP}_{\text{MRT}}^{\infty} ={\lambda_{2}}\sqrt {\frac{\beta} {{\eta \theta {\rho_{d}}}}}. $$

(16)

In the case of imperfect CSI (0 < ζ < 1)

$$\begin{array}{@{}rcl@{}} \text{SOP}_{\text{RAS}}^{\infty} &\,=\,& 1 \,-\, 2{e^{- \frac{{{{\bar x}_{2}}{\lambda_{1}}}}{{\zeta \omega} } - {\lambda_{2}}{{\bar x}_{2}}}} \sqrt {\frac{{{{\bar x}_{2}}\left( {1 - \zeta} \right)\beta {\lambda_{2}}}}{\zeta} } {K_{1}}\left( 2\sqrt {\frac{\bar x_{2}\left( {1 \,-\, \zeta} \right)\beta {\lambda_{2}}}{\zeta} } \right), \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} \text{SOP}_{\text{TAS}}^{\infty} &\,=\,& 1 + 2\sum\limits_{n = 1}^{N} \binom{N}{n} {\left( { - 1} \right)^{n}}{e^{- \frac{{n{{\bar x}_{2}}{\lambda_{1}}}}{{\zeta \omega} } - {\lambda_{2}}{{\bar x}_{2}}}} \\ & &\qquad \qquad \times \sqrt {\frac{{n{{\bar x}_{2}}\left( {1 - \zeta} \right)\beta {\lambda_{2}}}}{\zeta} } {K_{1}}\left( 2 \sqrt {\frac{ n\bar x_{2}\left( {1 - \zeta} \right)\beta {\lambda_{2}}}{\zeta} } \right), \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} \text{SOP}_{\text{MRT}}^{\infty} &\,=\,& 1 - \sum\limits_{n = 0}^{N - 1} \frac{2}{{n!}}{e^{- \frac{{\bar x_{2}}{\lambda_{1}}}{\zeta \omega} - {\lambda_{2}}{{\bar x}_{2}}}}\sum\limits_{k = 0}^{n} \binom{n}{k} {\left( {{\mu_{0}}\alpha} \right)^{n - k}} \\ & &\qquad \qquad \times {\left( {\frac{{{\mu_{0}}\alpha {{\bar x}_{2}}\beta {\lambda_{2}}}}{{\beta - 1}}} \right)^{\frac{{k + 1}}{2}}} {K_{1 - k}}\left( {2\sqrt {\frac{{{\mu_{0}}\alpha {{\bar x}_{2}}\beta {\lambda_{2}}}}{{\beta - 1}}}} \right), \end{array} $$

(19)

where $\omega =\rho _{s}/\rho _{d},\mu _{0}=(1-\zeta )(1-\theta )\frac {\rho _{s}}{\lambda _{1}}$,and $\bar x_{2}=(1-\zeta )(\beta -1)\frac {\omega }{\lambda _{1}}$.

Proof

See Appendix B. □

3.2 The average secrecy capacity

The ASC of the proposed system is given by

$$ \bar R_{\sec} = \mathbb{E}\left\{{\left[{\mathcal{C}_{\text{d}}} - {\mathcal{C}_{\text{r}}} \right]}^{+}\right\}. $$

(20)

Using the fact that $\mathbb {E}\left \{ {\max \left \{ {x,y} \right \}} \right \} \geqslant \max \left \{ {\mathbb {E}\left \{ x \right \},\mathbb {E}\left \{ y \right \}} \right \}$, the lower bound of the ASC can be determined as

$$ \bar R_{\text{sec,low}} = \left[\bar{\mathcal{C}}_{d} - \bar{\mathcal{C}}_{r} \right]^{+} , $$

(21)

where $\bar {\mathcal {C}}_{d} = \mathbb {E}\left \{ {{{\log }_{2}}\left ({1 + {\gamma _{d}}} \right )} \right \}$, and $\bar {\mathcal {C}}_{r} = \mathbb {E}\left \{ \log _{2} \left (1 + \gamma _{r}\right ) \right \}$.

We first derive the closed-form expression for $\bar {\mathcal {C}}_{d}$. Considering the function f(x) = ln (1 + e ^x), it can be seen that f(x) is a convex function and linearly increases for high values of x. Then, using Jensen’s inequality for f(x), we can approximate $\bar {\mathcal {C}}_{d}$ as

$$\begin{array}{@{}rcl@{}} {\mathcal{C}_{d}} & =& \mathbb{E}\left\{ {{{\log}_{2}}\left( {1 + {e^{\ln \left( {{\gamma_{d}}} \right)}}} \right)} \right\} \\ & \approx& {\log_{2}}\left( {1 + {e^{\mathbb{E}\left\{ {\ln \left( {{\gamma_{d}}} \right)} \right\}}}} \right) \\ & \approx& {\log_{2}}\left( {1 + {e^{\ln \left( {\zeta \left( {1 - \theta} \right){\rho_{s}}} \right) + {\mathcal{J}_{1}} + {\mathcal{J}_{2}} - {\mathcal{J}_{3}}}}} \right), \end{array} $$

(22)

where $\mathcal {J}_{1} = \mathbb {E}\left \{ {\ln \left (X_{1} \right )} \right \}$, $\mathcal {J}_{2} = \mathbb {E}\left \{ {\ln \left (X_{2} \right )} \right \}$, and $\mathcal {J}_{3} = \mathbb {E}\left \{ {\ln \left (X_{2}\mu + \kappa \right )} \right \}$.

Proposition 3

$\bar {\mathcal {C}}_{d}$ of the RAS, TAS, and MRT schemes can be approximated as

$$\begin{array}{@{}rcl@{}} \mathcal{C}_{d}^{\text{RAS}} &\!\approx\!& {\log_{2}}\left( 1 + \exp \left( \ln \left( \tfrac{\zeta \left( {1 - \theta} \right){\rho_{s}}}{\kappa {\lambda_{1}}{\lambda_{2}}} \right) + 2{\Psi} \left( 1 \right) + e^{\frac{{{\lambda_{2}}\kappa} }{\mu} }Ei\left( - \tfrac{\lambda_{2} \kappa} {\mu} \right) \right) \right), \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} \mathcal{C}_{d}^{\text{TAS}} &\!\approx\!& {\log_{2}}\left( 1 + \exp \left( \ln \left( \tfrac{\zeta \left( 1 - \theta \right){\rho_{s}}}{\kappa {\lambda_{2}}} \right) + 2{\Psi} \left( 1 \right) + e^{\frac{{{\lambda_{2}}\kappa} }{\mu} } Ei\left( - \tfrac{{{\lambda_{2}}\kappa} }{\mu} \right)\right.\right.\\ &&\quad \,-\, \left.\left. N\sum\limits_{n = 0}^{N - 1} \binom{N-1}{n} \frac{{{{\left( { - 1} \right)}^{n}}}}{{\left( {n + 1} \right)}}\ln \left( {\left( {n + 1} \right){\lambda_{1}}} \right) \right) \right), \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} \mathcal{C}_{d}^{\text{MRT}} &\!\approx\!& {\log_{2}}\left( 1 + \exp \left( \ln \left( \tfrac{\zeta \left( {1 - \theta} \right){\rho_{s}}}{\kappa {\lambda_{1}}{\lambda_{2}}} \right) + \psi \left( N \right) + {\Psi} \left( 1 \right)\right.\right.\\ &&\quad + \left.\left. {e^{\frac{{{\lambda_{2}}\kappa} }{\mu} }}Ei\left( - \tfrac{\lambda_{2}\kappa} {\mu} \right) \right) \right). \end{array} $$

(25)

Proof

See Appendix C. □

Next, we derive the closed-form expression for $\bar {\mathcal {C}}_{r}$. According to [17], $\bar {\mathcal {C}}_{r}$ is calculated as

$$ \bar{\mathcal{C}}_{r} = \mathbb{E}\left\{ {{{\log}_{2}}\left( {1 + {\gamma_{r}}} \right)} \right\} = \frac{1}{\ln(2)}\int\limits_{0}^{\infty} \frac{{1 - {F_{{\gamma_{r}}}}\left( \gamma \right)}}{{1 + \gamma} }. $$

(26)

Proposition 4

$\bar {\mathcal {C}}_{r}$ of the RAS scheme is calculated as follows.

• For λ ₁≠λ ₂ ζ ω :

  $$\begin{array}{@{}rcl@{}} \bar{\mathcal{C}}_r^{{\text{RAS}}} &\approx& \frac{1}{\ln \left( 2 \right)\left( {1 - \frac{{\lambda_{1}}}{{\lambda_{2}\zeta \omega}}} \right)} \left( {e^{\frac{{\mu\lambda_{2}\zeta \omega} }{{\zeta \left( {1 - \theta} \right)\rho_{s}}}}} Ei\left( {\tfrac{{ - \mu \lambda_{2}\omega} }{{\left( {1 - \theta} \right)\rho_{s}}}} \right)\right.\\ &&- \left. {e^{\frac{{\lambda_{1}\mu} }{{\zeta \left( {1 - \theta} \right)\rho_{s}}}}}Ei\left( \tfrac{ - \lambda_{1}\mu} {\zeta \left( {1 - \theta} \right)\rho_{s}} \right) \right). \end{array} $$

  (27)

• For λ ₁ = λ ₂ ζ ω :

  $$ \bar{\mathcal{C}}_{r}^{\text{RAS}} \approx \frac{1}{{\ln \left( 2 \right)}}\left( 1 + \frac{{\lambda_{1}\mu}}{{\zeta \left( {1 - \theta} \right)\rho_{s}}}{e^{\frac{{\lambda_{1}\mu} }{{\zeta \left( {1 - \theta} \right)\rho_{s}}}}}Ei\left( \tfrac{{ - \lambda_{1}\mu} }{{\zeta \left( {1 - \theta} \right)\rho_{s}}} \right) \right). $$

  (28)

  $\bar {\mathcal {C}}_{r}$ofthe TAS scheme is calculated as follows.

• For n λ ₁≠λ ₂ ζ ω:

  $$\begin{array}{@{}rcl@{}} {}\bar{\mathcal{C}}_r^{{\text{TAS}}} &\approx &\sum\limits_{n = 1}^N \binom{N}{n} \frac{\left( { - 1} \right)^{n+1}}{\ln(2) \left( 1 - \frac{{n{\lambda _1}}}{\lambda _2 \zeta \omega} \right)} \\ & &\times \left( {e^{\frac{{\mu {\lambda _2}\zeta \omega} }{{\zeta \left( {1 - \theta} \right){\rho _s}}}}}Ei\left( { \tfrac{-\mu {\lambda _2}\omega} {{\left( {1 - \theta} \right){\rho _s}}}} \right) - {e^{\frac{{n{\lambda _1}\mu} }{{\zeta \left( {1 - \theta} \right){\rho _s}}}}}Ei\left( \tfrac{-n{\lambda _1}\mu} {{\zeta \left( {1 - \theta} \right){\rho _s}}} \right) \right).\\ \end{array} $$

  (29)

• For n λ ₁ = λ ₂ ζ ω:

  $$ \bar{\mathcal{C}}_{r}^{{\text{TAS}}} \approx \sum\limits_{n = 1}^N \binom{N}{n} \frac{ (-1)^{n+1}}{\ln \left( 2 \right)} \left( {\!1 \,+\, \frac{{n\lambda_{1}\mu} }{{\zeta \left( {1 - \theta} \right)\rho_{s}}}{e^{\frac{{n\lambda_{1}\mu} }{{\zeta \left( {1 - \theta} \right)\rho_{s}}}}}Ei\left( { \tfrac{{-n\lambda_{1}\mu}}{{\zeta \left( {1 - \theta} \right)\rho_{s}}}} \right)} \right). $$

  (30)

  $\bar {\mathcal {C}}_{r}$ofthe MRT scheme is calculated as follows.

• For λ ₁≠λ ₂ ζ ω:

  $$\begin{array}{@{}rcl@{}} {}\bar{\mathcal{C}}_{r}^{{\text{MRT}}} &\!\approx\! &\frac{{{\lambda _2}}}{{\ln \left( 2 \right)}}\sum\limits_{n = 0}^{N - 1} {\frac{1}{{n!}}{{\left( {\frac{{{\lambda _1}}}{{\zeta \omega} }} \right)}^n}} \sum\limits_{k = 0}^n \binom{n}{k} {\left( {\frac{\mu} {{\left( {1 - \theta} \right){\rho _d}}}} \right)^{n - k}}{\Gamma} \left( {k \,+\, 1} \right)\\ &&\!\times \left( {{A_0}{e^{\frac{{{\lambda _1}\mu} }{{\zeta \left( {1 - \theta} \right){\rho _s}}}}}{\Gamma} \left( {n + 1} \right)} {\Gamma} \left( - n,\tfrac{{{\lambda _1}\mu} }{{\zeta \left( {1 - \theta} \right){\rho _s}}} \right)\right.\\ && \!+ \left. \sum\limits_{i = 1}^{k + 1} \frac{{{A_i}}}{{\lambda _2^i}}{{\left( {\frac{{\zeta \omega {\lambda _2}}}{{{\lambda _1}}}} \right)}^{n + 1}}{\Gamma} \left( {n \,+\, 1} \right) {U\left( {n \,+\, 1,n - i \,+\, 2;\tfrac{{\omega {\lambda _2}\mu} }{{\left( {1 - \theta} \right){\rho _s}}}} \right)} \right) . \\ \end{array} $$

  (31)

• For λ ₁ = λ ₂ ζ ω:

  $$\begin{array}{@{}rcl@{}} {}\bar{\mathcal{C}}_r^{{\text{MRT}}} &\!\approx\! &\frac{{{\lambda _2}}}{{\ln \left( 2 \right)}}\sum\limits_{n = 0}^{N - 1} {\frac{1}{{n!}}{{\left( {\frac{{{\lambda _1}}}{{\zeta \omega} }} \right)}^n}} \sum\limits_{k = 0}^n \binom{n}{k} {\left( {\frac{\mu} {{\left( {1 - \theta} \right){\rho _d}}}} \right)^{n - k}}\\ &&\times {\left( {\frac{{\zeta \omega} }{{{\lambda _1}}}} \right)^{k + 1}} {\Gamma} \left( {k \,+\, 1} \right) {\Gamma} \left( {n \,+\, 1} \right)U\left( {n \,+\, 1,n - k;\tfrac{{\omega {\lambda _2}\mu} }{{\left( {1 - \theta} \right){\rho _s}}}} \right).\\ \end{array} $$

  (32)

  where ${A_{0}} = {\left ({{\lambda _{2}} - \tfrac {{{\lambda _{1}}}}{{\zeta \omega } }} \right )^{- k - 1}}$and ${A_{i}} = \tfrac {{ - {\lambda _{1}}}}{{\zeta \omega } }{\left ({{\lambda _{2}} - \tfrac {{{\lambda _{1}}}}{{\zeta \omega } }} \right )^{- k - 2 + i}}$.

Proof

See Appendix D. □

4 Results and discussion

In this section, we present numerical results to validate the analytical expressions presented in Section 3. Unless otherwise specified, we set η = 0.5,𝜃 = 0.5,τ = 3,R _{t h} = 1b i t s/s/H z,N = 3, and ${\sigma _{0}^{2}}=1$. The coordinates in the two-dimensional plane of S, D, and R are set to (0,0),(2,0), and (d,0.2), respectively.

In Fig. 2, we show the SOP and its asymptote when both S and D increase their transmit powers, i.e., ρ _s = ρ _d = ρ. As can be seen, when ρ increases, the SOP for perfect CSI remarkably improves while that in the case of imperfect CSI converges to a determined value. These results can be explained using the effect of the noise caused by imperfect CSI on the SOP. Particularly, in the case of imperfect CSI, the strength of this noise linearly increases with the signal strength; hence, the SOP converges at high ρ values. Comparing the three antenna schemes, we observe that the MRT provides a better SOP than the TAS scheme, and both the MRT and TAS schemes outperform the RAS scheme; especially in the case of imperfect CSI, these trends become even clearer. Additionally, the SOP is an increasing function of R _{t h} . This result can be explained by Eq. 12, in which the probability that R _sec is less than R _{t h} becomes greater as R _{t h} increases. Moreover, as shown in Fig. 2, the asymptote agrees well with the exact SOP at high ρ values.

Fig. 2

The effect of ρ on the SOP and its asymptote in the cases of a ζ = 1 and b ζ = 0.9. Other parameters: d = 1 and ρ _s = ρ _d = ρ

In Fig. 3, we investigate the effect of 𝜃 on the SOP and ASC. The value of 𝜃 is varied from 0 to 1. As shown, the SOP and ASC improve as 𝜃 increases from 0 to the corresponding optimal power-splitting ratios, at which point the SOP or ASC achieve the best values, and they rapidly become worse with further increases in 𝜃. This result can be explained using the effect of 𝜃 on the harvested energy and the signal strength portion used for information decoding at R. At low 𝜃 values, the secrecy performance is low due to the low harvested energy at R; at high 𝜃 values, the secrecy performance is low due to the low input signal strength at the information-decoding component of R. Thus, the optimal power-splitting ratio 𝜃 ^∗, which balances the signal strength portions employed for the information-receiving task and energy-harvesting task at R, provides the best secrecy performance. The value of 𝜃 ^∗ for each performance metric is determined using a numerical search method. Moreover, the effects of η on the SOP and ASC are also examined. It can be observed that the secrecy performance is enhanced as η increases.

Fig. 3

The effect of 𝜃 on the SOP and ASC. Other parameters: d = 1,ρ _s = ρ _d = 25(d B) and R _s = 2(b i t s/s e c/H z)

In Fig. 4, we investigate the effects of ρ _s and ρ _d on the optimal SOP and optimal ASC in different scenarios: S₁, S₂, and S₃. We fix ρ _s and ρ _d in scenarios S₁ and S₂, respectively, while we vary their values in scenario S₃. Comparing the three antenna schemes, it can be observed that the MRT scheme provide the best secrecy performance, whereas the RAS scheme yields the poorest secrecy performance. Moreover, we consider the secrecy performance in two cases, perfect CSI (see Fig. 4a, b) and imperfect CSI with ζ = 0.9 (see Fig. 4c, d).

Fig. 4

The effect of ρ _s and ρ _d on the optimal SOP and optimal ASC. Other parameters: d = 1 and R _{t h} = 2(b i t s/s e c/H z)

In the case of perfect CSI, the optimal SOP is an increasing function of ρ, and the optimal ASC is a decreasing function of ρ. Moreover, as ρ increases, the secrecy performance in scenarios S₁ and S₂ converges, whereas it linearly increases in scenario S₃. These results can be explained using the trends of $\mathcal {C}_{r}$ and $\mathcal {C}_{d}$ in the three scenarios. In scenario S₁, the fixed ρ _s value leads to a fixed $\mathcal {C}_{d}$, which limits the secrecy performance. In scenario S₂, the same increasing rates of $\mathcal {C}_{r}$ and $\mathcal {C}_{d}$ cause the secrecy performance to converge. In scenario S₃, the increasing trends of ρ _s and ρ _d leads to substantial growth in $\mathcal {C}_{d}$ and the limit in $\mathcal {C}_{r}$, respectively, which contribute to the remarkable increase in secrecy performance. Additionally, at low ρ values, the secrecy performance in scenario S₂ overcomes those in scenarios S₁ and S₃.

In the case of imperfect CSI, the secrecy performance in scenarios S₁ and S₃ decreases and converges, whereas that in scenario S₂ improves at first and then degrades. Comparing these results with that in the perfect CSI case, we have the follows. For scenario S₁, the secrecy performance trends in both perfect CSI and imperfect CSI cases are similar, except for the limit of each case. In contrast, the secrecy performance trends in the perfect CSI and imperfect CSI cases are different for scenarios S₂ and S₃. This is because of the effect of the noise caused by imperfect CSI. Particularly, for scenario S₂, both $\mathcal {C}_{r}$ and $\mathcal {C}_{d}$ converge to a value in which the convergence rate of $\mathcal {C}_{d}$ is higher than that of $\mathcal {C}_{r}$ due to the effect of the AN; therefore, the optimal SOP and optimal ASC follow a convex function and a concave function of ρ, respectively. In scenario S₃, $\mathcal {C}_{d}$ converges to a higher value than $\mathcal {C}_{r}$ due to the effect of the AN, hence, the secrecy performance converges to a non-zero value. On the other hand, at high ρ values, the secrecy performance in scenario S₁ becomes better than that in the other scenarios, whereas at low ρ values, the secrecy performance in scenario S₂ outperforms that in the other scenarios.

In Fig. 5, we present the optimal SOP and optimal ASC results in term of the trade-off between the transmit powers of S and D. The overall transmit power over noise power is ρ _Σ = 10³, i.e., ρ _s + ρ _d = ρ _Σ. As shown in Fig. 5, the highest secrecy performance is obtained as ρ _s is between 0 and ρ _Σ, and the secrecy performance rapidly decreases as ρ _s tends to 0 or ρ _Σ. These results show an important role of the destination-assisted jamming in creating the positive secrecy capacity, such as, with low destination-assisted jamming signal’s powers, the secure communication between S and D does not exist. Moreover, it can be seen that the peaks of the optimal SOP and ASC curves move toward to the left (the decreasing trend of ρ _s ) when ζ increases. Comparing three considered schemes, the peaks of the optimal SOP and ASC curves for the TAS scheme is located in the left side of that for the RAS scheme and in the right side of that for the MRT scheme. For all values of ρ _s ∈ (0,ρ _Σ], the MRT scheme yields the best secrecy performance while the RAS scheme gives a lowest secrecy performance.

Fig. 5

The optimal SOP and optimal ASC in term of the trade-off between ρ _s and ρ _d (ρ _s + ρ _d = ρ _Σ). Other parameter: d = 1 and ρ _Σ = 30(d B)

In Fig. 6, we investigate the effects of N and ζ on the optimal SOP and optimal ASC. From Eq. 9, it can be seen that the signal strength that can be decoded at the receiver decreases and the noise power caused by the imperfect CSI increases as ζ decreases; therefore, the secrecy performance degrades as ζ decreases. On the other hand, it can be seen in Eq. 9 that, when S is equipped with a larger antenna, the signal strength used for information decoding at the receiver for the TAS and MRT schemes is enhanced, whereas the noise power caused by the imperfect CSI does not change. Therefore, when N increases, the secrecy performances for both the MRT and TAS schemes improves. Moreover, it can be seen in Fig. 5 that the MRT scheme outperform the TAS scheme for all values of ζ.

Fig. 6

The effect of ζ on the SOP and ASC. Other parameter: d = 1,ρ _s = ρ _d = 25(d B) and R _s = 2(b i t s/s e c/H z)

In Fig. 7, we investigate the effect of the relay’s location on the optimal SOP and optimal ASC. As shown, the secrecy performance improves as d increases from 0 to an optimal distance, and then it slightly degrades with further increase in d. These results can be explained by using the effect of the R − D link on the AN at R and the overall noise at D. When R is near S, the AN’s strength becomes weak due to the decreasing trend of the R − D channel gain, hence, the secrecy performance is low. In contrast, when R is near D, the overall noise at D increases because of an increasing trend in the R − D channel gain; therefore, the secrecy performance slightly degrades. Comparing with the conventional cooperative SWIPT system (which uses the trusted relay in which a high performance is achieved when R is located near S), our proposed system achieves high performance when R is located between S and D. Moreover, it can be observed from Fig. 7 that the optimal SOP is approximately zero if R is close to S, such as d < 0.2, for the case of ζ = 1, and d < 0.4 for the case of ζ = 0.9.

Fig. 7

The effect of the relay’s location on the optimal SOP and optimal ASC. Other parameters: ρ _s = ρ _d = 15(d B)

5 Conclusion

In this paper, we studied the secure communication of a cooperative system using an energy-harvesting untrusted relay. The source was equipped with multiple antennas and used TAS and MRT to enhance the harvested energy at the relay. For performance comparison, RAS was examined. Additionally, the destination-assisted jamming was employed to create a positive secrecy capacity. The analytical expression of the SOP and ASC for the two cases, i.e., perfect CSI and imperfect CSI, were derived; moreover, the closed-form expression for the SOP at high-power levels was also presented. We used the Monte Carlo simulations to verify the accuracy of the analytical results. Our results demonstrated that (1) the secrecy performance in both the perfect CSI case and imperfect CSI is improved as the source’s antennas increases. (2) MRT performs better than TAS; and both MRT and TAS provide a significant improvement in secrecy performance compared with RAS. Especially in the imperfect CSI’s case, these trends has shown clearer. (3) The best location for the untrusted relay is between the source and the destination. Moreover, the effects of various system parameters, such as the channel correlation coefficient, energy-harvesting efficiency, secrecy rate threshold, power-splitting ratio, and transmit powers on secrecy performance were studied, and these findings provide valuable insight into system design.

Appendices

Appendix A: Proof of Proposition 1

Let x ₁,…,x _N be N exponential RVs with a rate parameter λ, and the PDF and CDF of x _n , 1 ≤ n ≤ N, are respectively given by

$$\begin{array}{@{}rcl@{}} f(\lambda ;x) & =& \lambda e^{- \lambda x}, \end{array} $$

(33)

$$\begin{array}{@{}rcl@{}} F(\lambda ;x)& =& 1 - e^{- \lambda x}. \end{array} $$

(34)

Let us define Y = max{x ₁,…,x _N } and $Z={\sum }_{n=1}^{N} x_{n}$. The CDFs of Y and Z are respectively given by

$$\begin{array}{@{}rcl@{}} {F_{Y}}\left( {\lambda ,N;x} \right) &\,=\,& F{\left( {\lambda ;x} \right)^{N}} \,=\, 1 \,+\, \sum\limits_{n = 1}^{N} \binom{N}{n} {\left( { - 1} \right)^{n}}{e^{- n\lambda x}}, \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} {F_{Z}}\left( {\lambda ,N;x} \right) &=& 1 - {e^{- \lambda x}}\sum\limits_{n = 0}^{N - 1} {\frac{{{{\left( {\lambda x} \right)}^{n}}}}{{n!}}}. \end{array} $$

(36)

Next, we rewrite Eq. 12 as

$$ \text{SOP} \,=\, 1 - \int\limits_{{{\bar x}_{1}}}^{+ \infty} {\left( {1 \,-\, {F_{{X_{1}}}}\left( {{\lambda_{1}},N;\tfrac{{\beta - 1}}{{\zeta \left( {1 - \theta} \right){\rho_{s}}{\Xi} \left( {x;\beta} \right)}}} \right)} \right)} {f_{{X_{2}}}}\left( {{\lambda_{2}};x} \right)dx. $$

(37)

where ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ are the cumulative distribution function (CDF) of X ₁ and the probability density function (PDF) of X ₂, respectively.

1.1 A.1 Calculation for SOP_RAS

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 37 with F(λ ₁; x) and f(λ ₂; x), respectively, we obtain Eq. 13.

1.2 A.2 Calculation for SOP_TAS

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 37 with F _Y (λ ₁,N; x) and f(λ ₂; x), respectively, we obtain Eq. 14.

1.3 A.3 Calculation for SOP_MRT

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 37 with F _Z (λ ₁,N; x) and f(λ ₂; x), respectively, we obtain Eq. 15.

Finally, Proposition 1 is proved.

Appendix B: Proof of Proposition 2

1.1 B.1 Calculation for case of perfect CSI (ζ = 1)

In this case, we have $\mu =1, {\Xi } \left ({x;\beta } \right ) \approx \frac {x}{{x + \kappa } }$, and ${\bar x_{1}} \approx \sqrt {\frac {{\beta } }{{\eta \theta {\rho _{d}}}}}$. Therefore, Eq. 12 can be approximated as

$$ \text{SOP} = 1 - \Pr \left( {{X_{1}} > {{\bar x}_{3}}|{X_{2}} > {{\bar x}_{1}}} \right) \approx {F_{{X_{2}}}}\left( {{\lambda_{2}};{{\bar x}_{1}}} \right), $$

(38)

where ${\bar x_{3}} = \frac {{\left ({\beta - 1} \right )}}{{\left ({1 - \theta } \right ){\rho _{s}}}}\left ({1 + \frac {\kappa } {{{X_{2}}}}} \right )$, and the approximation in Eq. (38) is obtained due to the fact that $\mathop {\lim } \limits _{\left ({{\rho _{s}},{\rho _{d}}} \right ) \to \left ({\infty ,\infty } \right )} \frac {{{{\bar x}_{3}}}}{{{{\bar x}_{1}}}} = 0$.

Using the series representation of the exponential function given in [15, Eq. (1.211.1)], we can prove (16).

1.2 B.2 Calculation for case of perfect CSI (0 < ζ < 1)

In this case, we have $\mu \approx {\mu _{0}}: = \left ({1 - \zeta } \right )\left ({1 - \theta } \right )\tfrac {{{\rho _{s}}}}{{{\lambda _{1}}}}$ and ${\Xi } \left ({x;\beta } \right ) \approx \frac {1}{\mu } - \frac {\beta } {{\left ({1 - \theta } \right ){\rho _{d}}{X_{2}} + \mu } }$. Therefore, $\frac {1}{{\Xi \left ({x;\beta } \right )}}$ can be approximated by

$$ \frac{1}{{\Xi \left( {x;\beta} \right)}} \approx \mu \left( {1 + \frac{{\left( {1 - \zeta} \right)\omega \beta} }{{{\lambda_{1}}\left( {{X_{2}} - {{\bar x}_{2}}} \right)}}} \right). $$

(39)

Then, the asymptotic functions for the SOP are calculated by

$$\begin{array}{@{}rcl@{}} \text{SOP}^{\infty} &\,=\,& 1 \,-\, \Pr \left( {X_{1}} \!>\! \tfrac{{\bar x}_{2}}{{\omega \zeta} }\left( 1 \,+\, \tfrac{{\left( {1 - \zeta} \right)\omega \beta} }{{{\lambda_{1}}\left( {{X_{2}} - {{\bar x}_{2}}} \right)}} \right)|{X_{2}} \!>\! {{\bar x}_{2}} \right) \\ &\,=\,& 1 \,-\, \int\limits_{{\bar x}_{2}}^{\infty} \left( 1 \,-\, {F_{{X_{1}}}}\left( {{\lambda_{1}},N;\tfrac{{\bar x}_{2}}{{\omega \zeta} } \left( {1 \,+\, \tfrac{\left( {1 - \zeta} \right)\omega \beta} {{\lambda_{1}}\left( {x - {{\bar x}_{2}}} \right)}} \right)} \right) \right) {f_{{X_{2}}}}\left( {{\lambda_{2}};x} \right)dx. \\ \end{array} $$

(40)

Let us define $t=x-\bar x_{2}$, Eq. 40 can be rewritten as

$$ \text{SOP}^{\infty} \,=\, 1 - \int\limits_{0}^{\infty} \left( 1 \,-\, F_{{X_{1}}}\left( {{\lambda_{1}},N;\tfrac{{\bar x}_{2}}{\omega \zeta} \left( {1 \,+\, \tfrac{{\left( {1 - \zeta} \right)\omega \beta} }{{{\lambda_{1}}t}}} \right)} \right) \right) {f_{{X_{2}}}}\left( {{\lambda_{2}};t \,+\, {{\bar x}_{2}}} \right)dt. $$

(41)

1.2.1 B.2.1 Calculation for $\textup {SOP}_{\textup {RAS}}^{\infty }$

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and $f_{{X_{2}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 41 with F(λ ₁; x) and f(λ ₂; x), respectively, we have

$$ \text{SOP}^{\infty} = 1 - {\lambda_{2}}{e^{- \frac{{{\lambda_{1}}{{\bar x}_{2}}}}{{\omega \zeta} } - {\lambda_{2}}{{\bar x}_{2}}}}\int\limits_{0}^{\infty} {e^{- \frac{ {{\bar x}_{2}} \left( 1 - \zeta \right) \beta } {{\zeta} t} - {\lambda_{2}}t}} dt. $$

(42)

With the help of [15, Eq. (3.471.9)], Eq. 42 can be expressed as Eq. 17.

1.2.2 B.2.2 Calculation for $\textup {SOP}_{\textup {TAS}}^{\infty }$

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 41 with F _Y (λ ₁,N; x) and f(λ ₂; x), respectively, and using the same step in the calculation for SOPRAS∞, we obtain Eq. 18.

1.2.3 B.2.3 Calculation for $\textup {SOP}_{\textup {MRT}}^{\infty }$

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 41 with F _Z (λ ₁,N; x) and f(λ ₂; x), respectively, and using the same step in the calculation for SOPRAS∞, we obtain Eq. 19.

Finally, Proposition 2 is proved.

Appendix C: Proof of Proposition 3

1.1 C.1 Calculation for the RAS scheme

Using the PDFs of X ₁ and X ₂ for the RAS scheme given by f(λ ₁; x) and f(λ ₂; x), respectively, and [15, Eq.(4.352.1)], $\mathcal {J}_{1}$ and $\mathcal {J}_{2}$ for the RAS scheme are calculated as

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{1}^{{\text{RAS}}} &=& {\Psi} \left( 1 \right) - \ln \left( {{\lambda_{1}}} \right), \end{array} $$

(43)

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{2}^{{\text{RAS}}} &=& {\Psi} \left( 1 \right) - \ln \left( {{\lambda_{2}}} \right) \end{array} $$

(44)

Moreover, using the PDFs of X2 and [15, Eq.(4.337.1)], $\mathcal {J}_{3}$ for the RAS scheme is calculated as

$$ \mathcal{J}_{3}^{{\text{RAS}}} = \ln \left( \kappa \right) - {e^{\frac{{{\lambda_{2}}\kappa} }{\mu}}}Ei\left( { - \tfrac{{{\lambda_{2}}\kappa} }{\mu} } \right). $$

(45)

Substituting Eqs. 43, 44, and 45 into Eq. 22 yields (23).

1.2 C.2 Calculation for the TAS scheme

According to [18], the PDF of Y defined in Appendix A is given by

$$ {f_{Y}}\left( {\lambda ,N;x} \right) = Nf\left( {\lambda ;x} \right)F{\left( {\lambda ;x} \right)^{N-1}}. $$

(46)

Using the PDF of X ₁ for the TAS scheme given by f _Y (λ ₁,N; x) and [15, Eq.(4.352.1)], $\mathcal {J}_{1}$ for the TAS scheme is calculated as

$$ \mathcal{J}_{1}^{{\text{TAS}}} = N\sum\limits_{n = 0}^{N - 1} \binom{N-1}{n} \frac{{{{\left( { - 1} \right)}^{n}}}}{{{n + 1}}}\left( {\Psi \left( 1 \right) - \ln \left( {\left( {n + 1} \right){\lambda_{1}}} \right)} \right). $$

(47)

Using the fact that $N\sum \limits _{n = 0}^{N - 1} \binom {N-1}{n} \frac {{{{\left ({ - 1} \right )}^{n}}}}{{\left ({n + 1} \right )}} = 1$, we can rewrite Eq. 47 as

$$ \mathcal{J}_{1}^{{\text{TAS}}} = {\Psi} \left( 1 \right) - N\sum\limits_{n = 0}^{N - 1} \binom{N-1}{n} \frac{{{{\left( { - 1} \right)}^{n}}}}{{ {n + 1}} }\ln \left( {\left( {n + 1} \right){\lambda_{1}}} \right). $$

(48)

Because $\mathcal {J}_{2}$ and $\mathcal {J}_{3}$ for the TAS scheme are the same as for the RAS scheme, Eq. 24 is obtained by substituting Eqs. 44, 45 and 48 into Eq. 22.

1.3 C.3 Calculation for the MRT scheme

According to [8], the PDF of Z defined in Appendix A is given by

$$ {f_{Z}}\left( {\lambda ,N;x} \right) = \frac{{{\lambda^{N}}{x^{N - 1}}}}{{\Gamma \left( N \right)}}{e^{- \lambda x}}. $$

(49)

Using the PDF of X ₁ for the MRT scheme given by f _Z (λ ₁,N; x) and [15, Eq.(4.352.1)], $\mathcal {J}_{1}$ for the MRT scheme is calculated as

$$ \mathcal{J}_{1}^{{\text{MRT}}} = \psi \left( N \right) - \ln \left( {{\lambda_{1}}} \right). $$

(50)

Because $\mathcal {J}_{2}$ and $\mathcal {J}_{3}$ for the MRT scheme are the same as for the RAS scheme, Eq. 25 is obtained by substituting Eqs. 44, 45, and 50 into Eq. 22.

Appendix D: Proof of Proposition 4

From Eq. 7, the PDF of γ _r is calculated as

$$\begin{array}{@{}rcl@{}} {F_{{\gamma_{r}}}}\left( \gamma \right) &\,=\,& \Pr \left( {{\gamma_{r}} < \gamma} \right)\\ &\,=\,& \int\limits_{0}^{\infty} {{F_{{X_{1}}}}\left( {{\lambda_{1}},N;\tfrac{{\gamma \left( {\left( {1 - \theta} \right){\rho_{d}}x + \mu} \right)}}{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}} \right)} {f_{{X_{2}}}}\left( {{\lambda_{2}};x} \right)dx.\\ \end{array} $$

(51)

1.1 D.1 Calculation for the RAS scheme

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 50 with F(λ ₁; x) and f(λ ₂; x), respectively, Eq. 50 can be expressed as

$$ {F_{{\gamma_{r}}}}\left( \gamma \right) = 1 - {\left( {\frac{{{\lambda_{1}}\gamma} }{{{\lambda_{2}}\zeta \omega} } + 1} \right)^{- 1}}{e^{- \frac{{{\lambda_{1}}\gamma \mu} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}. $$

(52)

Substituting Eqs. 50 into Eq. 26, we have the following:

$$ \bar{\mathcal{C}}_{r} = \frac{1}{{\ln \left( 2 \right)}}\int\limits_{0}^{\infty} \left( \tfrac{\lambda_{1} \gamma}{\lambda_{2} \zeta \omega} + 1 \right)^{-1} \left( {1 + \gamma} \right)^{-1} {e^{- \frac{{{\lambda_{1}}\gamma \mu} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}d\gamma. $$

(53)

In the case of λ ₁ ≠ λ ₂ ζ ω, $\left ({\tfrac {{{\lambda _{1} \gamma }}}{{{\lambda _{2}}\zeta \omega } } \,+\, 1} \right )^{-1} ({1 \,+\, \gamma } )^{-1}$ can be expressed as ${\left ({1 \,-\, \tfrac {{{\lambda _{1}}}}{{{\lambda _{2}}\zeta \omega } }} \right )^{- 1}}\left ({{{\left ({\gamma \,+\, 1} \right )}^{- 1}} \,-\, {{\left ({\gamma \,+\, {} \tfrac {{{\lambda _{2}}\zeta \omega } }{{{\lambda _{1}}}}} \right )}^{- 1}}} \right )$. Then, using [15, Eq.(3.383.10)], we obtain Eq. 27. In the case of λ ₁ = λ ₂ ζ ω, we obtain Eq. 28 with the help of [15, Eq. (3.353.2)].

1.2 D.2 Calculation for the TAS scheme

The result for the TAS scheme can be obtained by replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 50 with F _Y (λ ₁,N; x) and f(λ ₂; x), respectively, and using the same step as in Appendix D.1.

1.3 D.3 Calculation for the MRT scheme

Replacing ${F_{{X_{1}}}}\left ({{\lambda _{1}},N;x} \right )$ and ${f_{{X_{2}}}}\left ({{\lambda _{2}};x} \right )$ in Eq. 50 with F _Z (λ ₁,N; x) and f(λ ₂; x), respectively, and using [15, Eq.(8.350.2)], Eq. 50 can be expressed as

$$\begin{array}{@{}rcl@{}} {F_{{\gamma_{r}}}}\left( \gamma \right) &\,=\, &1 \,-\, {\lambda_{2}}{e^{- \frac{{{\lambda_{1}}\mu \gamma} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}\sum\limits_{n = 0}^{N - 1} {\frac{1}{{n!}}{{\left( {\frac{{{\lambda_{1}}\gamma} }{{\zeta \omega} }} \right)}^{n}}} \\ &&\!\times\! \sum\limits_{k = 0}^{n} \binom{n}{k} {\left( {\frac{\mu} {{\left( {1 \,-\, \theta} \right){\rho_{d}}}}} \right)^{n - k}}\frac{{\Gamma \left( {k \,+\, 1} \right)}}{{{{\left( {\frac{{{\lambda_{1}}\gamma} }{{\zeta \omega} } \,+\, {\lambda_{2}}} \right)}^{k + 1}}}}. \end{array} $$

(54)

Substituting Eq. 53 into Eq. 26, we have the following:

$$\begin{array}{@{}rcl@{}} \bar {\mathcal{C}}_{r} &= &\frac{{{\lambda_{2}}}}{{\ln \left( 2 \right)}}\sum\limits_{n = 0}^{N - 1} {\frac{1}{{n!}}{{\left( {\frac{{{\lambda_{1}}}}{{\zeta \omega} }} \right)}^{n}}} \sum\limits_{k = 0}^{n} \binom{n}{k} {\left( {\frac{\mu} {{\left( {1 - \theta} \right){\rho_{d}}}}} \right)^{n - k}} \\ &&\times {\Gamma} \left( {k + 1} \right)\int\limits_{0}^{\infty} {{\gamma^{n}}} \mathcal{I}\left( \gamma \right){e^{- \frac{{{\lambda_{1}}\mu \gamma} }{{\zeta \left( {1 - \theta} \right){\rho_{s}}}}}}d\gamma , \end{array} $$

(55)

where $\mathcal {I}\left (\gamma \right ) = {\left ({1 + \gamma } \right )^{- 1}}{\left ({\tfrac {{{\lambda _{1}}}}{{\zeta \omega } }\gamma + {\lambda _{2}}} \right )^{- k - 1}}$.

In the case of λ ₁≠λ ₂ ζ ω, $\mathcal {I}\left (\gamma \right )$ can be decomposed using partial fraction decomposition as follows.

$$ \mathcal{I}\left( \gamma \right) = \frac{{{A_{0}}}}{{\left( {1 + \gamma} \right)}} + \sum\limits_{i = 1}^{k + 1} {\frac{{{A_{i}}}}{{{{\left( {\frac{{{\lambda_{1}}}}{{\zeta \omega} }\gamma + {\lambda_{2}}} \right)}^{i}}}}}. $$

(56)

Substituting Eq. 55 into Eq. 54 and using [15, Eq.(3.383.10) and Eq.(9.211.4)], we obtain Eq. 31.

In the case of λ ₁ = λ ₂ ζ ω, $\mathcal {I}\left (\gamma \right ) = {\left ({\tfrac {{\zeta \omega } }{{{\lambda _{1}}}}} \right )^{k + 1}}{({\gamma + 1})^{- k - 2}}$. Then, with the help of [15, Eq. (9.211.4)], we obtain Eq. 32.