1 Introduction

The interaction force between tires and pavement surface plays a decisive role in the accelerating and braking performance of the car, and the analysis of tire load is a prerequisite for the study of accelerating and braking performance (Barbosa et al., 2022). Tire is one of the key systems of the car, with the role of loading, vibration damping, transferring force and torque, which directly affects the reliability, stability, safety, comfort and other performance of the car. Tires have highly nonlinear characteristics, and their mechanical properties are affected by a variety of factors, such as air pressure, temperature, material, friction, raceway speed, and pavement conditions (Zhang et al., 2021; Diaz et al., 2016). Tire load (longitudinal force, lateral force, and vertical force) is an important index to evaluate the dynamic performance of tires, and it is also the key to vehicle dynamic performance analysis. Tire mechanical performance parameters can be obtained through theoretical studies, numerical simulations and experimental methods.

In theoretical studies, the mechanical properties of tires are analyzed qualitatively by establishing numerical models of tires, and the commonly used methods include the empirical formula method and the semi-empirical formula method (Gorelov & Komissarov, 2016), among which magic formula of the tire model is most widely used. For tire deformation, stiffness and load analysis, the finite-element analysis method is usually used (Baranowski et al., 2016; Wei & Olatunbosun, 2014). The colloid in the tire model is simulated using hyperelastic constitutive model, such as Ogden model, Mooney–Rivlin model, and NeoHooke model. The simulation accuracy depends on the parameter settings of the constitutive model and the contact parameters of the tire and the pavement surface. However, it is difficult to obtain the parameters accurately and comprehensively.

While building a tire dynamics model, most of the tire dynamics analysis is performed by modifying the parameters of the tire model in ADAMS software. The tire models include PAC89, PAC94, PAC2002, Fiala, UA, Swift, and FTire (Bosch et al., 2016; Babulal et al., 2015). The pavement incentive frequencies from 0 to 50 Hz can basically meet the tire dynamics simulation requirements, and only the effective frequencies of Swift and FTire tires meet this requirement, while the effective frequencies of tires are below 8 Hz. the Swift model adopts the equivalent pavement profile method, which differs from the actual input pavement profile; the Swift model requires a pavement sampling interval of 0.1–0.2 m, which enlarges the error of the pavement model; the above factors reduce the simulation accuracy of Swift model. The FTire model is a nonlinear tire model that recognizes many different formats of pavement files and has high computational accuracy; however, the model requires many parameters and requires a lot of experiments to obtain these parameters, which is expensive. At the same time, the model occupies large computational resources and the simulation efficiency is low.

Pneumatic tire models have highly nonlinear characteristics, and most of the existing tire parameters are obtained based on steady-state tire mechanics experiments (Guo et al., 2001; Kutzbach et al., 2019). However, in the accelerating and braking process of a vehicle, tires often show unsteady dynamic characteristics, which makes the mathematical and simulation models of pneumatic tires unable to accurately reflect the unsteady dynamic characteristics of tires. Therefore, tire dynamic tests in vehicle’s normal running process have been an important tool for tire load research.

Compared with theoretical studies and numerical simulations, test methods can significantly improve the accuracy of tire load analysis, but there are also large differences between different test methods. Tire load test methods include indirect test methods and direct test methods, indirect test methods are mainly used to calculate the tire load by testing the tire deformation data, and the commonly used test method is to analyze the tire deformation by means of a high-speed camera or an acceleration sensor embedded in the tire (Gao et al., 2021; Tonkovich et al., 2012). However, indirect testing methods can only accurately analyze tire load in a single direction at a time (Jin & Yin, 2015). The direct test method uses a dynamometer to measure the tire load directly, and among the many methods, the most commonly used direct test method is the six-component test method, which can accurately analyze the tire load in six directions, but the high cost of the six-component test method, the long test cycle, and the poor versatility of the test equipment limit its widespread use.

To obtain tire longitudinal force, lateral force and vertical force efficiently and accurately, a simple and effective tire load calculation method needs to be designed. In this paper, by establishing an analytical model for tire compound deformation identification, tire deformation is back-calculated based on steering knuckle arm acceleration signal, and combining tire stiffness test and six-component test data, a tire load calculation and correction method applicable to accelerating and braking conditions is proposed to provide a theoretical basis and reference for analyzing the dynamic change characteristics of tire load.

2 Theoretical Model

In vehicle’s normal running process, the pneumatic tire is a complex force system, and the load analysis of the tire involves kinematics, dynamics, thermodynamics, friction mechanics and other subject areas, and is also affected by structural nonlinearity, material nonlinearity and other factors. Especially in the vehicle accelerating and braking conditions, the tire appears compound deformation, including torsional deformation, roll deformation, trim deformation, as well as roll deformation and torsional deformation. It is difficult for most of the current test methods to identify the compound deformation comprehensively and accurately, which in turn affects the calculation of tire load. Therefore, it is necessary to establish an analytical model for tire compound deformation identification, to explore the test method of tire compound deformation, and to perform the calculation of tire load (Baffet et al., 2009).

The tire load changes dynamically in vehicle’s normal running process. On the flat random pavement, the vehicle driving at a constant speed, tire load dynamic change amplitude is small, the tire deformation can be considered as the steady-state deformation. When the vehicle is accelerating and braking, tire load dynamic change amplitude is larger, the composition of the load is also more complex, the tire deformation is multi-directional composited at this time, and tire working state is mostly in the unsteady state. During the vehicle dynamics analysis, the tire load data need to be collected.

The wheels are mounted on the steering knuckle arms and rotate around the steering knuckle arm, and the deformation of the tire is transmitted to the steering knuckle arm as shown in Fig. 1a. The movement of the steering knuckle arm can indirectly reflect the deformation of the tire contact point A. The upper end point C of the steering knuckle arm is connected to the upper control arm by a ball hinge, the lower end point D of the steering knuckle arm is connected to the lower control arm by a ball hinge, and the front-end point B of the steering knuckle arm is connected to the steering tie rod type by a ball hinge.

Fig. 1
figure 1

Spatial motion model of floating coordinate system. a Translational model. b Rotation model. c Projection

Full size image

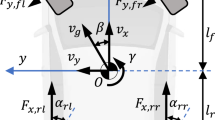
The plane where points B, C and D are located is E1E2E3E4, and the plane E1E2E3E4 produces X-, Y-, Z-, Rx-, Ry- and Rz-directional motions in the whole vehicle coordinate system. The X-directional, Y-directional and Z-directional motions of plane E1E2E3E4 approximately represent the longitudinal, roll and torsional deformation at the tire junction A. The Rx-, Ry- and Rz-directional motions of plane E1E2E3E4 represent the roll deformation α, trim deformation β and torsional deformation γ of the tire at location A, as shown in Fig. 1b.

Figure 1c represents the projection schematic of plane E1E2E3E4 in the coordinate system of the whole vehicle, the roll deformation α is the angle between the projection of side E1E2 in the XOY plane and the X-axis; trim deformation β is the angle between the projection of side E1E4 in the XOZ plane and the Z-axis; torsional deformation γ is the angle between the projection of edge E3E4 in the YOZ plane and the Z-axis.

Floating coordinate system fixed on the steering knuckle arm Ki = {I; ui, vi, wi} moves with the steering knuckle arm, and the whole vehicle coordinate system KOs = {Os; xs, ys, zs} is fixed. To describe the spatial motion of the steering knuckle arm, the floating coordinate system needs to be transformed in the whole vehicle coordinate system. In this way, the positions of the points on the steering knuckle arm in the whole vehicle coordinate system are determined. The initial equilibrium position, in the coordinate system, Ki has the same direction as the coordinate system KOs. When the coordinate system Ki is rotated around the coordinate system KOs by an angle of {φ1, φ2, φ3}, we can obtain the coordinate system Ki1 = {I1; ui1, vi1, wi1}. The conversion of the floating coordinate system Ki1 relative to the whole vehicle coordinate system KOs is

$$\begin{aligned} \left[ \begin{gathered} x_{Oi} \hfill \\ y_{Oi} \hfill \\ z_{Oi} \hfill \\ \end{gathered} \right] = & \left[ \begin{gathered} u_{i} \hfill \\ v_{i} \hfill \\ w_{i} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \varphi_{1} } & {\sin \varphi_{1} } \\ 0 & { - \sin \varphi_{1} } & {\cos \varphi_{1} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\cos \varphi_{2} } & 0 & { - \sin \varphi_{2} } \\ 0 & 1 & 0 \\ {\sin \varphi_{2} } & 0 & {\cos \varphi_{2} } \\ \end{array} } \right] \cdot \\ \quad \left[ {\begin{array}{*{20}c} {\cos \varphi_{3} } & {\sin \varphi_{3} } & 0 \\ { - \sin \varphi_{3} } & {\cos \varphi_{3} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ \begin{gathered} u_{i1} \hfill \\ v_{i1} \hfill \\ w_{i1} \hfill \\ \end{gathered} \right] \\ \end{aligned}$$
(1)

The floating coordinate system will rotate around the self-axis while rotating around the whole vehicle coordinate system. The floating coordinate system Ki rotates around the self-axis by angle of {ϕ1, ϕ2, ϕ3}, obtain the coordinate system Ki2 = {I2; ui2, vi2, wi2}. The result of converting the Ki2 coordinate system relative to the Ki1 coordinate system is

$$\begin{gathered} \left[ \begin{gathered} u_{i1} \hfill \\ v_{i1} \hfill \\ w_{i1} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi_{1} } & {\sin \phi_{1} } \\ 0 & { - \sin \phi_{1} } & {\cos \phi_{1} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\cos \phi_{2} } & 0 & { - \sin \phi_{2} } \\ 0 & 1 & 0 \\ {\sin \phi_{2} } & 0 & {\cos \phi_{2} } \\ \end{array} } \right] \cdot \\ \left[ {\begin{array}{*{20}c} {\cos \phi_{3} } & {\sin \phi_{3} } & 0 \\ { - \sin \phi_{3} } & {\cos \phi_{3} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ \begin{gathered} u_{i2} \hfill \\ v_{i2} \hfill \\ w_{i2} \hfill \\ \end{gathered} \right] \\ \end{gathered}$$
(2)

The result of converting the Ki2 coordinate system relative to the KOs coordinate system is

$$\begin{aligned} \left[ \begin{gathered} x_{Oi} \hfill \\ y_{Oi} \hfill \\ z_{Oi} \hfill \\ \end{gathered} \right] = & \left[ \begin{gathered} u_{i} \hfill \\ v_{i} \hfill \\ w_{i} \hfill \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \varphi_{1} } & {\sin \varphi_{1} } \\ 0 & { - \sin \varphi_{1} } & {\cos \varphi_{1} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\cos \varphi_{2} } & 0 & { - \sin \varphi_{2} } \\ 0 & 1 & 0 \\ {\sin \varphi_{2} } & 0 & {\cos \varphi_{2} } \\ \end{array} } \right] \cdot \\ \quad \left[ {\begin{array}{*{20}c} {\cos \varphi_{3} } & {\sin \varphi_{3} } & 0 \\ { - \sin \varphi_{3} } & {\cos \varphi_{3} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi_{1} } & {\sin \phi_{1} } \\ 0 & { - \sin \phi_{1} } & {\cos \phi_{1} } \\ \end{array} } \right] \cdot \\ \quad \left[ {\begin{array}{*{20}c} {\cos \phi_{2} } & 0 & { - \sin \phi_{2} } \\ 0 & 1 & 0 \\ {\sin \phi_{2} } & 0 & {\cos \phi_{2} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {\cos \phi_{3} } & {\sin \phi_{3} } & 0 \\ { - \sin \phi_{3} } & {\cos \phi_{3} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ \begin{gathered} u_{i2} \hfill \\ v_{i2} \hfill \\ w_{i2} \hfill \\ \end{gathered} \right] \\ \end{aligned}$$
(3)

The points on the steering knuckle arm move reciprocally in their respective equilibrium positions during the vehicle travel, as shown in Fig. 2a. Figure 2b shows the projection of the steering knuckle arm in the XOZ plane of the whole vehicle coordinate system. Figure 2c shows the projection of the knuckle arm in the YOZ plane of the vehicle coordinate system. Figure 2d shows the projection of the steering knuckle arm in the XOY plane of the vehicle coordinate system. By analyzing the dynamic change of spatial position of point B, point C and point D, the displacement of the steering knuckle arm in six directions can be calculated.

Fig. 2
figure 2

Schematic diagram of the steering arm motion. a Spatial motion state of steering arm. b XOZ plane projection schematic. c YOZ plane projection schematic. d XOY plane projection schematic

Full size image

In the equilibrium position, the spatial states of point B, point C and point D in a fixed coordinate system are

$$\left[ \begin{gathered} B \hfill \\ C \hfill \\ D \hfill \\ \end{gathered} \right]_{0} = \left[ {\begin{array}{*{20}c} {x_{B} } & {y_{B} } & {z_{B} } \\ {x_{C} } & {y_{C} } & {z_{C} } \\ {x_{D} } & {y_{D} } & {z_{D} } \\ \end{array} } \right]_{0}$$
(4)

During the motion, the spatial states of point B, point C and point D in the floating coordinate system are

$$\left[ \begin{gathered} B \hfill \\ C \hfill \\ D \hfill \\ \end{gathered} \right]_{1} = \left[ {\begin{array}{*{20}c} {u_{B} } & {v_{B} } & {w_{B} } \\ {u_{C} } & {v_{C} } & {w_{C} } \\ {u_{D} } & {v_{D} } & {w_{D} } \\ \end{array} } \right]_{1}$$
(5)

Due to the constraint relationship between the steering knuckle arm and the control arm, the steering knuckle arm mainly rotates around the w-axis with a turning angle of φw, and the self-propagation angle in other directions is very small. The steering knuckle arm is in the whole vehicle coordinate system KOs The translational displacement in the whole vehicle coordinate system is {dis(x), dis(y), dis(z)} and the rotation angle is {α, β, γz}. Since the control arm is attached to the body by rubber bushings, the main steering knuckle arm mainly produces an oscillation about the X-axis with an angle of rotation α. Convert KB1 = {B; uB, vB, wB}1, KC1 = {C; uC, vC, wC}1 with KD1 = {D; uD, vD, wD}1. The result of the conversion relative to the fixed coordinate system is

$$\begin{aligned} \left[ \begin{gathered} x_{B} \hfill \\ y_{B} \hfill \\ z_{B} \hfill \\ \end{gathered} \right]_{1} = & \left[ \begin{gathered} x_{B} \hfill \\ y_{B} \hfill \\ z_{B} \hfill \\ \end{gathered} \right]_{0} + \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \alpha } & {\sin \alpha } \\ 0 & { - \sin \alpha } & {\cos \alpha } \\ \end{array} } \right] \cdot \\ \quad \left[ {\begin{array}{*{20}c} {\cos \varphi_{w} } & {\sin \varphi_{w} } & 0 \\ { - \sin \varphi_{w} } & {\cos \varphi_{w} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ \begin{gathered} u_{B} \hfill \\ v_{B} \hfill \\ w_{B} \hfill \\ \end{gathered} \right]_{1} \\ \end{aligned}$$
(6)
$$\begin{aligned} \left[ \begin{gathered} x_{C} \hfill \\ y_{C} \hfill \\ z_{C} \hfill \\ \end{gathered} \right]_{1} = & \left[ \begin{gathered} x_{C} \hfill \\ y_{C} \hfill \\ z_{C} \hfill \\ \end{gathered} \right]_{0} + \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \alpha } & {\sin \alpha } \\ 0 & { - \sin \alpha } & {\cos \alpha } \\ \end{array} } \right] \cdot \\ \quad \left[ {\begin{array}{*{20}c} {\cos \varphi_{w} } & {\sin \varphi_{w} } & 0 \\ { - \sin \varphi_{w} } & {\cos \varphi_{w} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ \begin{gathered} u_{C} \hfill \\ v_{C} \hfill \\ w_{C} \hfill \\ \end{gathered} \right]_{1} \\ \end{aligned}$$
(7)
$$\begin{aligned} \left[ \begin{gathered} x_{D} \hfill \\ y_{D} \hfill \\ z_{D} \hfill \\ \end{gathered} \right]_{1} = & \left[ \begin{gathered} x_{D} \hfill \\ y_{D} \hfill \\ z_{D} \hfill \\ \end{gathered} \right]_{0} + \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \alpha } & {\sin \alpha } \\ 0 & { - \sin \alpha } & {\cos \alpha } \\ \end{array} } \right] \cdot \\ \quad \left[ {\begin{array}{*{20}c} {\cos \varphi_{w} } & {\sin \varphi_{w} } & 0 \\ { - \sin \varphi_{w} } & {\cos \varphi_{w} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \cdot \left[ \begin{gathered} u_{D} \hfill \\ v_{D} \hfill \\ w_{D} \hfill \\ \end{gathered} \right]_{1} \\ \end{aligned}$$
(8)

The steering knuckle arm is in the whole vehicle coordinate system KOs The translational displacement in the whole vehicle coordinate system is

$$\left\{ \begin{gathered} dis(x) = x_{C1} - x_{D1} = dis_{C} (x) - dis_{D} (x) \hfill \\ dis(y) = y_{C1} - y_{D1} = dis_{C} (y) - dis_{D} (y) \hfill \\ dis(z) = z_{C1} = z_{D1} = dis_{C} (z) = dis_{D} (z) \hfill \\ \end{gathered} \right.$$
(9)

The steering knuckle arm is in the whole vehicle coordinate system KOs The rotation angle in the whole vehicle coordinate system is

$$\left\{ \begin{gathered} \alpha = \arctan \frac{{dis_{C} (y) - dis_{D} (y)}}{h} \hfill \\ \gamma = \varphi_{w} = \arctan \frac{{dis_{B} (y) - dis_{C} (y)}}{L} \hfill \\ \end{gathered} \right.$$
(10)

where h represents the vertical distance between point C and point D, and L represents the horizontal distance between point C and point B.

Therefore, it is possible to consider {dis(x), dis(y), dis(z)} as the deformation of the tire grounding point. Tire load can be expressed as

$$\left[ {\begin{array}{*{20}c} {F_{X} } \\ {F_{Y} } \\ {F_{Z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {F_{Z0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {k_{x} } & {} & {} \\ {} & {k_{y} } & {} \\ {} & {} & {k_{z} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {dis(x)} \\ {dis(y)} \\ {dis(z)} \\ \end{array} } \right]$$
(11)

where kx represents the longitudinal stiffness of the tire, ky represents the lateral stiffness of the tire, kz represents the radial stiffness of the tire, and Fz0 represents the static load of the tire.

3 Experiment and Data Analysis

3.1 Test Description

The calculation of tire load requires tire stiffness data. Figure 3a shows the radial stiffness, lateral stiffness and longitudinal stiffness tests of the tire. The tire load is 80% of the rated load, rated load and 120% of the rated load, respectively. For the radial stiffness test, the test bench is moved in the w-direction; for the longitudinal stiffness test, the test bench is moved in the u-direction; for the lateral stiffness test, the test bench is moved in the v-direction; the speed of the test bench is 50 mm/min.

Fig. 3
figure 3

Tire test. a Tire stiffness test. b Steering knuckle arm acceleration test. c Tire six-component test

Full size image

To measure the motion of the steering knuckle arm, it is necessary to arrange a three-way acceleration sensor at each point B, C and D, as shown in Fig. 3b. The displacement signal is back-calculated from the acceleration signal, the deformation of the tire is calculated according to Eqs. (9) and (10), and the tire load is calculated according to Eq. (11). Before processing the acceleration signal, the data need to be filtered and drifted, and the cutoff frequency is selected as 0.5 Hz. To verify the accuracy of the tire load calculation method proposed in this paper, the six-component test was carried out on the vehicle, as shown in Fig. 3c. The test pavement was a dry asphalt pavement, the test vehicle was fully loaded, and the accelerating test, constant speed test and braking test were carried out respectively.

3.2 Data Analysis

During the test, the driver continuously completed the accelerating, keeping a constant speed and braking operations, and recorded the change curve of the vehicle speed, as shown in Fig. 4. Stage 1 is accelerating, initial speed is 0 km/h, maximum speed is 100 km/h, acceleration time is 19.1 s. Stage 2 is keeping a constant speed at 100 km/h, travel time is 5.9 s. Stage 3 is braking, speed drops from 100 to 0 km/h, braking time is 5 s. The speed curve in the figure shows that the accelerating and braking of the vehicle are quite smooth, and the tires are slipping in the initial stage during accelerating.

Fig. 4
figure 4

Vehicle speed curve

Full size image

By collecting the acceleration data of the steering knuckle arm, and filtering and de-drifting them, and carrying out quadratic integration calculation, the displacement of the steering knuckle arm in the whole vehicle coordinate system is obtained as shown in Fig. 5, which also represents the deformation of the tire junction point. In the acceleration stage 1, the deformation of the tire junction point A gradually increases, the trim deformation is −X direction and the deformation is the largest; the roll deformation and torsional deformation fluctuate randomly near the equilibrium position, and the deformation in both directions is comparable. In the constant speed stage 2, the roll deformation is the largest, and the trim deformation is relative to the torsional deformation. In braking stage 3, the trim deformation is + X direction and the deformation is maximum; the roll deformation and the torsional deformation fluctuate randomly near the equilibrium position, and the deformation in both directions is comparable. The maximum value of trim deformation of the tire in braking stage is 2.5 times of the maximum value of trim deformation of the tire in accelerating stage.

Fig. 5
figure 5

Tire deformation data

Full size image

Equation (11) shows that tire load estimation requires measuring the tire deformation data with the tire stiffness data. The experimental results of tire stiffness are shown in Table 1. The lateral stiffness decreases with the increase of tire load, and the stiffness increases with the increase of load in all other directions. The calculation results of the tire load are compared with the results of the six-component test to verify the accuracy of the tire load calculation method proposed in this paper.

Table 1 Tire stiffness data
Full size table

At 100% rated load condition, the comparison between the dynamic tire load and calculated test results according to Eq. (11) is shown in Fig. 6, and the trend of the tire load calculation curve and the test curve is basically consisting. Figure 6a shows the comparison data of the longitudinal force of the tire. In the accelerating stage 1, the calculated value of the maximum longitudinal load is 1988.6 N and the test value is 1219.2 N, the error between them is 39.7%, this error is mainly caused by the large fluctuation of the calculated value. In the constant speed stage 2, the calculated value of the maximum longitudinal load is 168.7 N, and the test value is 112.9 N, with an error of 33.1%. In decelerating stage 3, maximum calculated value of longitudinal load is 6257.7 N, and the test value is 5230.4 N, with an error of 16.4%. The goodness of fit between the two curves in the time period of 0–30 s is 84.8%.

Fig. 6
figure 6

Tire load comparison data. a Longitudinal load data. b Lateral load data. c Vertical load data

Full size image

Figure 6b shows the comparison data of the lateral force of the tire. In the accelerating stage 1, the maximum calculated value of the lateral load is 245.7 N, and the test value is 155.1 N, and the error between them is 36.9%. In the constant speed stage 2, the calculated value of the maximum lateral load is 144.3 N, and the test value is 95.7 N, with an error of 33.7%. In decelerating stage 3, the maximum calculated value of the lateral load is 337.4 N and the test value is 287.7 N, with an error of 14.7%. Tire load calculation curve has a poor goodness of fit with the test curve.

Figure 6c shows the comparison data of tire vertical force. In accelerating stage 1, maximum calculated value of vertical load is 9617.9 N and the test value is 8145.4 N, with an error of 15.3%. In the constant speed stage 2, the maximum calculated value of vertical load is 8429.2 N, and the test value is 7954.8 N, with an error of 5.6%. In decelerating stage 3, the maximum calculated value of vertical load is 6257.7 N and the test value is 5230.4 N, with an error of 16.4%. The goodness of fit between the two curves in the time period of 0–30 s is 84.8%.

3.3 Correction Method

To improve the calculation accuracy of the dynamic tire load, the calculation method needs to be corrected, and the main contents of the correction include the acceleration data filtering processing frequency and the accurate selection of the tire stiffness. Figure 7 shows the tire vertical load amplitude-frequency characteristic curve, the frequency range of calculated value is 0–30 Hz, and the frequency range of test value is 1.0–20 Hz, which leads to the error. The calculated value is around 0.5 Hz versus calculated value is 25.5 Hz, which further magnifies the error between them. In the paper, the suspension type analyzed is double wishbone suspension. The results of data processing with different cutoff frequencies are different. If the low-frequency signal is not filtered out, the displacement data obtained from the acceleration signal by quadratic integration will drift. When the cutoff frequency is 1.0 Hz, the displacement data fluctuate in the equilibrium position, which is consistent with the reality. Since the natural frequency of different suspension is different, the cutoff frequency is different. The cutoff frequency of low-frequency signal filtering is selected according to: the processed data have no drift phenomenon, and the data are distributed near the equilibrium position. The data analysis of different suspensions shows that the low-frequency cutoff frequency usually ranges from 0.3 to 1.0 Hz. In the process of vehicle acceleration and braking, vehicle excitation mainly includes road excitation and wheel rotation excitation, and the excitation frequency is far less than 20 Hz. The excitation frequency of the power transmission system is usually greater than 20 Hz, and to avoid the influence of the power transmission system excitation on the calculation of wheel load, the high-frequency cutoff frequency of 20 Hz can meet the requirements. Therefore, the cutoff frequency range should be 1.0–20 Hz when processing the steering knuckle arm acceleration data.

Fig. 7
figure 7

Tire vertical force amplitude and frequency characteristics curve

Full size image

In accelerating and braking conditions, the front and rear axle loads of the vehicle change, which will lead to a change in tire stiffness. This is also the main factor that affects the accuracy of tire load calculation. Figure 8 shows the simplified mechanical model of the vehicle. According to the torque equilibrium, the front axle load in a constant speed driving condition is

$$F_{{\text{f}}} = m_{{\text{f}}} g = \frac{{L_{1} }}{{L_{1} + L_{2} }}m_{{\text{c}}} g$$
(12)

where mc represents the total mass, and L1 represents the distance from the center of mass to the front axis, and L2 represents the distance from the center of mass to the rear axis.

Fig. 8
figure 8

Simplified mechanical model of the vehicle

Full size image

Acceleration conditions, front axle load is

$$F_{{\text{f}}} = \frac{{m_{{\text{c}}} gL_{2} - m_{{\text{c}}} a_{1} h}}{{L_{1} + L_{2} }}$$
(13)

where h represents the height of the center of mass, and a1 represents the acceleration.

In braking condition, front axle load is

$$F_{{\text{f}}} = \frac{{m_{{\text{c}}} gL_{2} + m_{{\text{c}}} a_{2} h}}{{L_{1} + L_{2} }}$$
(14)

where a2 represents the deceleration rate.

The parameters of the test vehicle are shown in Table 2. According to Eqs. (12), (13) and (14), the front axle loads in the constant speed condition, accelerating condition and braking condition are calculated as 7840 N, 7560.4 N and 9101.8 N respectively. Figure 9 shows the tire stiffness test curves under different loads, according to the axle load calculation results, the longitudinal stiffness for the constant speed condition is 315.3 N/mm, lateral stiffness is 135.4 N/mm and radial stiffness is 340.7 N/mm. The longitudinal stiffness is 313.3 N/mm, the lateral stiffness is 134.6 N/mm and the radial stiffness is 340.5 N/mm in the accelerating condition; the longitudinal stiffness is 336.4 N/mm, the lateral stiffness is 131.5 N/mm and the radial stiffness is 357.5 N/mm for the braking condition. The correction coefficient is the ratio of the stiffness corresponding to the actual load of the tire and the stiffness corresponding to the 100% rated load, i.e., in the accelerating condition, the correction coefficient of the longitudinal load of the tire is 0.982, the correction coefficient of the lateral load is 0.994, and the correction coefficient of the radial load is 0.999. For the constant speed condition, the correction coefficient of longitudinal load is 1.054, the correction coefficient of lateral load is 0.971, and the correction coefficient of radial load is 1.049. The correction result of tire load is shown in Fig. 10.

Table 2 The basic parameters of the vehicle
Full size table
Fig. 9
figure 9

Tire vertical force amplitude and frequency characteristics curve

Full size image
Fig. 10
figure 10

Corrected tire load comparison data. a Longitudinal load data. b Lateral load data. c Vertical load data

Full size image

Figure 10a shows the comparative data of the longitudinal force of the tire. In the accelerating stage 1, the maximum longitudinal force is 1413.5 N, and the error with the test value is 14.3%. In the constant speed stage 2, the maximum longitudinal force is 138.1 N, with an error of 18.2% from the test value. In decelerating stage 3, the maximum longitudinal force was 5664.6 N, with an error of 7.7% from the test value. The goodness of fit between the two curves is 88.9% in the 0–30 s time period.

Figure 10b shows the comparison data of the lateral force of the tire. In the accelerating stage 1, the maximum lateral force is 187.4 N, which is 17.2% error from the test value. In the constant speed stage 2, the maximum lateral force was 115.5 N, with an error of 17.2% from the test value. In decelerating stage 3, the maximum lateral force was 314.9 N, with an error of 8.6% from the test value. Tire load calculation curve and test curve trend are basically consistent.

Figure 10c shows the comparison data of tire vertical force. In accelerating stage 1, the maximum vertical force is 8698.1 N, which is 6.4% error from the test value. In the constant speed stage 2, the maximum vertical force is 8235.3 N, which is 3.6% error from the test value. In decelerating stage 3, the maximum vertical force is 8972.8 N, which is 5.9% error from the test value.

Figure 10 shows that the accuracy of tire three-way load estimation is greater than 90% in the braking stage. However, the longitudinal load and lateral load of the tire are less than 90% at the acceleration stage and the uniform stage. Therefore, it is necessary to further improve the estimation accuracy of longitudinal load and lateral load in acceleration stage and uniform stage.

During driving, the tire deformation is a kind of compound deformation, which affects the estimation of tire longitudinal and lateral forces. Figure 11a is a schematic diagram of tire pure lateral stiffness test, Fig. 11b shows a schematic of tire lateral stiffness test under roll condition. According to the deformation characteristics of suspension, tire roll stiffness is more consistent with the actual condition. Figure 11c shows the lateral stiffness test of the tire under the roll condition. In the same way, the longitudinal stiffness of the tire is tested.

Fig. 11
figure 11

Tire roll stiffness test. a Schematic diagram of pure lateral stiffness test. b Schematic diagram of lateral stiffness test under roll condition. c Bench test of tire roll stiffness

Full size image

Under the load of 7840 N, the longitudinal stiffness of the tire is 289.7 N/mm, and the roll stiffness is 123.8 N/mm. Under the load of 7560.4 N, the longitudinal stiffness of the tire is 286 N/mm, and the roll stiffness is 123.2 N/mm. Under the load of 9101.8 N, the longitudinal stiffness of the tire is 331.2 N/mm, and the roll stiffness is 130.1 N/mm.

In the acceleration stage 1, the maximum longitudinal load is estimated to be 1270.3 N with an estimated accuracy of 95.9%; and the maximum lateral load is 171.5 N, the estimated accuracy is 90.4%. At constant velocity stage 2, the estimated maximum longitudinal load is 126.9 N, and the estimated accuracy is 89%. The maximum lateral load is estimated to be 104.6 N with an estimated accuracy of 91.5%. In deceleration stage 3, the estimated value of the maximum longitudinal load is 5576.8 N, the estimated precision is 93.8%; and the estimated value of the maximum lateral load is 311.5 N, the estimated precision is 92.4%.

4 Conclusion

An analytical model for tire compound deformation identification is established in this paper, the back-calculation of tire deformation based on the acceleration data of steering knuckle arm is discussed, and the calculation method of tire longitudinal force, lateral force and vertical force with the combination of tire stiffness are obtained. To improve the calculation accuracy of dynamic tire load, a correction method is proposed in this paper, and the calculated value is compared with the test value, which proves that the calculation and correction method proposed in this paper can correctly reflect the dynamic change characteristics of tire load in accelerating and braking conditions.