1 Introduction

A minimal surface in three-dimensional Euclidean space \(\mathbb {R}^3\) is a surface with zero mean curvature H everywhere. It is well known that, besides a plane, the only minimal surface of the form \(z=f(x)+g(y)\) for two real functions f and g is the Scherk’s surface ([12])

$$\begin{aligned} z(x,y)=\frac{1}{a}\left( \log (| \cos (ay)|)-\log (|\cos (ax)|)\right) ,\ a>0. \end{aligned}$$
(1)

In this particular case with \(z=f(x)+g(x)\), the equation \(H=0\) can be solved using separation of variables. A surface \(z=f(x)+g(y)\) can also be expressed as the sum of two planar curves, namely, \(\alpha (x)=(x,0,f(x))\) and \(\beta (y)=(0,y,g(y))\). Another minimal surface which can be written as the sum of two curves, which was already known by Lie, is the helicoid \(\phi (u,v)=(\cos {v}\cos {u},\cos {v}\sin {u},u)\), which is obtained as the sum of a circular helix \(\alpha \) with itself, that is, \(\phi (u,v)=\alpha (u)+\alpha (v)\) ([11, § 77]). Indeed, if we consider the helix \(\alpha (s)=(\cos {s},\sin {s},s)/2\), the change of coordinates \(u=(s+t)/2, v=(s-t)/2\) gives

$$\begin{aligned} \alpha (s)+\alpha (t)= & {} \left( \frac{1}{2}(\cos {s}+\cos {t}),\frac{1}{2}(\sin {s}+\sin {t}),s+t\right) \\= & {} \left( \frac{1}{2}(\cos (u+v)+\cos (u-v)),\frac{1}{2}(\sin (u+v)+\sin (u-v)),u\right) \\= & {} \phi (u,v). \end{aligned}$$

In general, a surface \(S\subset \mathbb {R}^3\) is called a translation surface if it can be expressed in a parametric form as

$$\begin{aligned} \phi (s,t)=\alpha (s)+\beta (t), \end{aligned}$$

where \(\alpha :I\subset \mathbb {R}\rightarrow \mathbb {R}^3\), \(\beta :J\subset \mathbb {R}\rightarrow \mathbb {R}^3\), are two regular curves with \(\alpha ^\prime (s)\times \beta '(t)\not =0\), which are called generators of S. A translation surface has the property that the translations of a parametric curve \(s=c\) by \(\beta (t)\) remain in S (similarly for the parametric curves \(t=c\)). These surfaces were initially introduced by Sophus Lie and attracted the interest of geometers studying certain special types, [1, 4, 10, 13]. In fact, and in the context of complex curves, Lie proved that an analytic surface is a minimal surface if and only if it can be represented as the sum of an isotropic complex curve and its complex conjugate [7], see also [11, § 148].

It has been an open problem for a long time whether the plane, the helicoid, and the Scherk surface are the only minimal translation surfaces in \(\mathbb {R}^3\). For example, the surface described in (1) belongs to a more general family of translation surfaces discovered by Scherk of minimal surfaces where both generators are planar curves but not necessarily in orthogonal planes. A partial result to this question was given in [3], where the authors showed that if one of the generator curves lies in a plane, then the surface is a plane or a Scherk surface. Following the same idea of separation of variables, it is possible to extend this type of problems to find translation surfaces in other ambient spaces prescribing other curvatures: see for example, [5, 8, 9, 14, 15]. The proofs of such results are usually rather long and tedious computations involving a number of subcases. Thus it seems necessary to give different techniques to the problem, especially in order to consider the general case that the generators are spatial curves, which has never been studied up to today.

This paper presents a new approach to the construction of minimal translation surfaces generated by two spatial curves. We characterize in Theorem 2.3 all the minimal translation surfaces in terms of the curvature \(\kappa \) and the torsion \(\tau \) of the generators, namely, it is necessary that \(\kappa ^2 \tau \) is constant. In Theorem 3.2 we give a description of such surfaces as a two-parametric family of surfaces in Euclidean space. As a consequence of our results, we provide many examples of minimal translation surfaces whose generators are spatial curves. For example, we prove (Corollary 3.3):

If \(\beta =\beta (t)\) is a regular non planar curve such that \(\kappa ^2\tau \) is constant and \(\beta ^\prime (t)\) lies in a Euclidean cone, then \(\phi (s,t)=\beta (s)+\beta (t)\) defines a minimal surface.

2 A Characterization of a Minimal Translation Surface

Let \(\phi (s,t)=\alpha (s)+\beta (t)\) be a minimal immersed surface in Euclidean space \(\mathbb {R}^3\). Since in the case that \(\alpha \) and/or \(\beta \) are planar curves, the description of the surface is known, we will assume in this section that \(\alpha \) and \(\beta \) are non-planar curves. Denote by \(\langle ,\rangle \) the Euclidean metric of \(\mathbb {R}^3\).

Let’s assume that \(\alpha \) and \(\beta \) are parametrized by the arc-length. It is straightforward that the minimality condition \(H=0\) of the surface \(\phi (s,t)\) is equivalent to

$$\begin{aligned} \langle \alpha '(s),\beta '(t),\alpha ''(s)\rangle +\langle \alpha '(s),\beta '(t),\beta ''(t)\rangle =0 \end{aligned}$$

for all \(s\in I, t\in J\), that is,

$$\begin{aligned} \langle \alpha ''(s)\times \alpha '(s),\beta '(t)\rangle +\langle \alpha '(s),\beta '(t)\times \beta ''(t)\rangle =0, \end{aligned}$$
(2)

where \(\times \) stands for the vectorial product of \(\mathbb {R}^3\). We write \(\mathbb {R}^6=\mathbb {R}^3\times \mathbb {R}^3\) and consider the vector subspaces of \(\mathbb {R}^6\) defined by

$$\begin{aligned} H_1= & {} \text{ span }\{(\alpha ^{\prime \prime }(s)\times \alpha ^{\prime }(s),\alpha ^\prime (s)): s\in I\}, \\ H_2= & {} \text{ span }\{(\beta ^\prime (t),\beta ^\prime (t) \times \beta ^{\prime \prime }(t)): t\in J\}. \end{aligned}$$

Lemma 2.1

The subspaces \(H_1\) and \(H_2\) are perpendicular and \(\text{ dim }(H_1)=\text{ dim }(H_2)=3.\)

Proof

The orthogonality property is a consequence of (2). Assume \(\text{ dim }(H_1)\le 2\). If this dimension is 2 (similarly if \(\text{ dim }(H_1)=1\)), then there exists \(\{(v_1,v_2),(w_1,w_2)\}\in \mathbb {R}^3\times \mathbb {R}^3\) two linearly independent vectors of \(\mathbb {R}^6\) that generate \(H_1\). Then for all \(s\in I\), there are \(\lambda (s),\mu (s)\in \mathbb {R}\) such that \((\alpha ^{\prime \prime }(s)\times \alpha ^{\prime }(s),\alpha ^\prime (s))=\lambda (s)(v_1,v_2)+\mu (s)(w_1,w_2)\). In particular, \(\alpha '(s)=\lambda (s)v_2+\mu (s)w_2\), which proves that \(\alpha \) is a planar curve, a contradiction. The same occurs for \(H_2\) and thus \(\text{ dim }(H_1),\text{ dim }(H_2)\ge 3\). Because \(H_1\perp H_2\), then \(H_1\cap H_2=\{0\}\) and this implies that \(H_1\) and \(H_2\) are 3-dimensional vector subspaces. \(\square \)

Lemma 2.2

Let A be a \(3\times 3\) matrix of real numbers. If there exists a curve X(t) in the unit sphere \({\mathbb {S}}^2\) such that

  1. (1)

    \(|AX| > 0\) and \(|X^\prime (t)|\ne 0\),

  2. (2)

    the set \(B=\{X,Y,Z\}\) with \(Z= AX/|AX|\) and \(Y=Z\times X\) is an orthonormal basis, and

  3. (3)

    the matrix of the transformation \(W\rightarrow AW\) with respect to the basis B is a matrix of the form \(\tilde{A}=\left( \begin{array}{c c c }0&{}0&{}a\\ 0 &{} b&{} c\\ a&{}d&{}e\end{array}\right) \) with \(a> 0\),

then A is a symmetric matrix.

Proof

Let us fix a \(t_0\) and let \(B_0=\{X(t_0),Y(t_0),Z(t_0)\}\). By hypothesis we know that the matrix of the transformation \(W\rightarrow AW\) with respect to the basis \(B_0\) is a matrix \(\tilde{A}_0=\left( \begin{array}{c c c }0&{}0&{}a_0\\ 0 &{} b_0&{} c_0\\ a_0&{}d_0&{}e_0\end{array}\right) \) for some \(a_0,b_0,c_0,d_0,e_0\) with \(a_0>0\). If \(Q_0\) is matrix whose first, second, and third columns are the vectors \(X(t_0)\), \(Y(t_0)\), and \(Z(t_0)\) respectively, then we have

$$\begin{aligned} A=Q_0\tilde{A}_0Q_0^T \end{aligned}$$
(3)

Likewise, if we denote by Q(t) the matrix whose first, second, and third columns are the vectors X(t), Y(t), and Z(t) respectively, then \(A=Q\tilde{A}Q^T\). Therefore, if \(P(t)=Q_0^TQ(t)\) then \(\tilde{A}_0=P\tilde{A}P^T\). Define \(\tilde{X}\), \(\tilde{Y}\), and \(\tilde{Z}\) to be the first, second, and third columns of the matrix P. Then we have

$$\begin{aligned} \tilde{A}_0 \tilde{X}=a \tilde{Z},\quad \tilde{A}_0 \tilde{Y}=b\tilde{Y} +d \tilde{Z},\quad \tilde{A}_0 \tilde{Z}=a \tilde{X}+c\tilde{Y}+e\tilde{Z} \end{aligned}$$

Notice that \(P(t_0)\) is the identity matrix. By (3), we will show that the matrix A is symmetric by showing that the matrix \(\tilde{A}_0\) is symmetric.

For every \(q=(x,y,z,u,v,w,r,s)\) near \(q_0=(1,0,0,a_0,b_0,c_0,d_0,e_0)\), we define the functions

$$\begin{aligned} p_1(q)= & {} \left( \begin{array}{c} x\\ y\\ z \end{array} \right) ,\quad p_3(q)=\frac{1}{\sqrt{ \langle \tilde{A}_0p_1,\tilde{A}_0p_1 \rangle }}\, \tilde{A}_0\left( \begin{array}{c} x\\ y\\ z \end{array}\right) , \quad p_2(q)=p_3\times p_1\\ f_0(q)= & {} x^2+y^2+z^2-1=\langle p_1,p_1\rangle -1\\ f_1(q)= & {} \langle \tilde{A}_0p_1,p_1\rangle \\ (f_2,f_3,f_4)^T= & {} \tilde{A}_0p_2-v p_2-r p_3\\ (f_5,f_6,f_7)^T= & {} \tilde{A}_0p_3-u p_1-w p_2-s p_3\\ (f_8,f_9,f_{10})^T= & {} \tilde{A}_0p_1-u p_3 \end{aligned}$$

Notice that \(f_i(q_0)=0\) for \(0\le i\le 10\) and moreover, the points \(\tilde{q}=(\tilde{x},\tilde{y},\tilde{z},\tilde{u},\tilde{v},\tilde{w},\tilde{r},\tilde{s})\) with \((\tilde{x},\tilde{y},\tilde{z})^T=\tilde{X}\) and \((\tilde{u},\tilde{v},\tilde{w},\tilde{r},\tilde{s})=(a,b,c,d,e)\), also satisfy that \(f_i(\tilde{q})=0\) for \(0\le i\le 10\). If we define \(F(q)=(f_0,f_1,f_3,f_4,f_5,f_6,f_7,f_{10})\), a direct computation shows that the determinant of the Jacobian matrix \(DF(q_0)\) is equal to \(4 (d_0-c_0) a_0\). Therefore we conclude that \(d_0=c_0\): otherwise, by the inverse function theorem, we would have that the only solution of \(F(q)=(0,\dots ,0)\) near \(q_0\) would be \(q_0\); but we know that all the points \(\tilde{q}\) are also solutions. This contradiction proves that \(\tilde{A}_0\) is a symmetric matrix. \(\square \)

Theorem 2.3

Let \(\phi (s,t)=\alpha (s)+\beta (t)\) be a minimal translation surface with \(\alpha \) and \(\beta \) non-planar curves parametrized by the arc-length. If \(\kappa \) and \(\tau \) denote the curvature and torsion of a generator of the surface, then \(\kappa ^2 \tau =C\) for some constant C. Moreover, there exists an invertible symmetric matrix A such that \(\beta ^\prime (t)\times \beta ^{\prime \prime }(t)=A\beta ^\prime (t)\).

Proof

Let \(T(t)=\beta '(t)\) be the tangent vector, N(t) the unit normal vector, and \(B(t)=T(t)\times N(t)\). The Frenet equations of the curve \(\beta \) are given by

$$\begin{aligned} \begin{array}{ccccc} T'&{}=&{} &{}\kappa N &{} \\ N'&{}=&{}-\kappa T&{} +&{} \tau B\\ B'&{}=&{} &{} -\tau N &{} \\ \end{array} \end{aligned}$$

and let \(H_2=\text{ span }\{(\beta ^\prime (t),\beta ^\prime (t) \times \beta ^{\prime \prime }(t_i)): t\in J\}\subset \mathbb {R}^6\). By Lemma 2.1, we know that \(\text{ dim }(H_2)=3\). Since the curve \(\beta \) is not contained in a plane, then its velocity vectors \(\beta '(t)\) are not contained in a plane and this allows to pick a basis for \(H_2\) of the form \(\{(v_1,w_1),(v_2,w_2),(v_3,w_3)\}\) where the vectors \(\{v_1,v_2,v_3\}\) are a basis of \(\mathbb {R}^3\). After a change of bases of the vector space \(H_2\), we can assume that \(\{v_1,v_2,v_3\}\) are the canonical basis of \(\mathbb {R}^3\) \(\{e_1=(1,0,0), e_2=(1,0,0), e_3=(1,0,0)\}\). Let \(\xi _i=\xi _i(t)\) be the (smooth) functions such that

$$\begin{aligned} (\beta ^\prime (t),\beta ^\prime (t)\times \beta ^{\prime \prime }(t))=\sum _{i=1}^3\xi _i(t) (e_i,w_i). \end{aligned}$$

Then \(\beta '(t)=\xi (t)\), with \(\xi =(\xi _1,\xi _2,\xi _3)\), and

$$\begin{aligned} \beta ^\prime (t)\times \beta ^{\prime \prime }(t)=\sum _{i=1}^3 \xi _i(t) w_i. \end{aligned}$$

Hence we write

$$\begin{aligned} \beta ^\prime (t)\times \beta ^{\prime \prime }(t)=\xi (t)\times \xi ^\prime (t)=A\xi (t), \end{aligned}$$
(4)

where A is the \(3\times 3\) matrix whose columns are \(w_1\), \(w_2\), and \(w_3\). Since the curve \(\beta \) is not planar, we will consider an open neighborhood when \(\kappa (t)\ne 0\). In terms of the Frenet frame we have that \(\xi =T\) and (4) reduces to

$$\begin{aligned} \kappa B=AT \end{aligned}$$
(5)

Differentiating Eq. (5) with respect to t, we obtain \(\kappa ^\prime B-\kappa \tau N=\kappa AN\) and therefore

$$\begin{aligned} AN=\frac{\kappa ^\prime }{\kappa }\, B- \tau N \end{aligned}$$
(6)

Differentiating Eq. (6) we have

$$\begin{aligned} -\kappa AT+\tau AB= \left( \frac{\kappa ^\prime }{\kappa }\right) ^\prime B-\tau \frac{\kappa ^\prime }{\kappa }\, N-\tau ^\prime N+\tau \kappa T-\tau ^2 B \end{aligned}$$

and therefore using Eq. (5) we obtain,

$$\begin{aligned} AB= \kappa \, T -\left( \frac{\kappa ^\prime }{\kappa }+ \frac{\tau ^\prime }{\tau }\right) \, N +\left( \frac{\kappa ^2}{\tau } -\tau + \frac{1}{\tau } \left( \frac{\kappa ^\prime }{\kappa }\right) ^\prime \right) B \end{aligned}$$
(7)

From Eqs. (5), (6), and (7), we conclude that the matrix of the linear transformation \(W\rightarrow AW\) in terms of the basis T, N, and B is given by

$$\begin{aligned} \tilde{A}(t)=\left( \begin{array}{c@{\quad }c@{\quad }c }0&{}0&{}\kappa (t) \\ 0 &{} -\tau (t) &{} d(t)\\ \kappa (t)&{}b(t)&{}c(t)\end{array}\right) \end{aligned}$$

with,

$$\begin{aligned} c(t)= & {} \frac{\kappa (t)^2}{\tau (t)} -\tau (t)+ \frac{1}{\tau (t)} \left( \frac{\kappa ^\prime (t)}{\kappa (t)}\right) ^\prime \\ d(t)= & {} -\frac{\kappa ^\prime (t)}{\kappa (t)}-\frac{\tau ^\prime (t)}{\tau (t)}\\ b(t)= & {} \frac{\kappa ^\prime (t)}{\kappa (t)}. \end{aligned}$$

Using Lemma 2.2 with \(X(t)=T(t)\) we conclude that the matrix A and \(\tilde{A}\) are symmetric. In particular, \(b=d\), and the matrix A is

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c }0&{}0&{}\kappa (t) \\ 0 &{} -\tau (t) &{} b(t)\\ \kappa (t)&{}b(t)&{}c(t)\end{array}\right) \end{aligned}$$
(8)

Moreover, the identity \(b(t)=d(t)\) implies

$$\begin{aligned} - \frac{\kappa ^\prime }{\kappa }-\frac{\tau ^\prime }{\tau }=\frac{\kappa ^\prime }{\kappa }, \end{aligned}$$

or equivalently, \(2\tau \kappa '+\kappa \tau '=0\). We conclude that \(\kappa ^2\, \tau =C\), where C is a constant. With the notation used in Lemma 2.2, notice that \(A=Q\tilde{A}Q^T\). Then the determinant of A is \(\text{ det }(A)=-\kappa ^2\tau =-C\). Let us observe that \(C\not =0\) because the curve \(\beta \) is non-planar. By symmetry of the arguments, the same holds for the curve \(\alpha \). \(\square \)

Remark

The condition \(\kappa ^2\tau =C\) for a spatial curve appears as the second equation that satisfies an elastica, a curve which is a critical point of the functional \(\int \kappa ^2 ds\) [6].

3 Description of Minimal Translation Surfaces

In this section we will describe all translation minimal surfaces whose generators are non-planar curves. We will essentially prove that there are as many translation surfaces as quadric cones in \(\mathbb {R}^3\): every quadratic form \(x\rightarrow \langle Ax,x\rangle \) with a non-singular symmetry matrix A, defines a translation surface \(\phi (s,t)=\beta (t)+\beta (s)\) such that \(\beta ^\prime (t)\) lies in the cone \(\{x\in \mathbb {R}^3:\langle Ax,x\rangle \}=0\}\) and such that the torsion times the square of the curvature of \(\beta \) equals the negative of the determinant of A.

The next result is immediate and it tells us how the matrix A in Theorem 2.3 changes by rigid motions and homotheties.

Lemma 3.1

Let \(\phi (s,t)=\alpha (s)+\beta (t)\) be a minimal translation surface and let A be the invertible symmetric matrix that satisfies \(\beta ^\prime \times \beta ^{\prime \prime }=A\beta ^\prime \).

  1. (1)

    If P is an orthogonal matrix P, then the surface \(P\circ \phi (s,t)\) is also a minimal translation surface, whose generators are \(\tilde{\alpha }(s)=P\circ \alpha (s)\) and \(\tilde{\beta }(t)=P\circ \beta (t)\) and the matrix \(\tilde{A}\) of Theorem 2.3 is \(\tilde{A}=PAP^T\).

  2. (2)

    Given a non-zero number \(\lambda \), the surface \(\lambda \phi (s,t)\) is a minimal translation surface whose generators are \(\tilde{\alpha }(s)=\lambda \alpha (s)\) and \(\tilde{\beta }(t)=\lambda \beta (t)\) and the matrix \(\tilde{A}\) of Theorem 2.3 is \(\tilde{A}=\lambda A\).

Using this lemma, we know that up to a rigid motion of a minimal translation surface \(\phi (s,t)=\alpha (s)+\beta (t)\), we may assume that the matrix A that satisfies \(\beta ^\prime \times \beta ^{\prime \prime }=A\beta ^\prime \), is diagonal. Let us denote by \(\lambda _1\), \(\lambda _2\), and \(\lambda _3\) the eigenvalues of A. Since \(\beta ^\prime (t)\in {\mathbb {S}}^2\), \(\beta '(t)\) lies in

$$\begin{aligned} \mathcal {C}=\mathbb {S}^2\cap \left\{ x(x_1,x_2,x_3)^T\in \mathbb {R}^3: \lambda _1 x_1^2+\lambda _2 x_2^2+\lambda _3 x_3^2 =0\right\} , \end{aligned}$$

then we conclude that not all \(\lambda _i\) can have the same sign. Furthermore, Lemma 3.1 allows to assume that \(\lambda _3=-1\) and \(\lambda _1\) and \(\lambda _2\) are positive real numbers. Therefore, up to rigid motion and dilation of the surface, we may assume that for some \(0<a<1\) and some \(0<b<1\) we have that

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c }\frac{1-a^2}{a^2}&{}0&{}0 \\ 0 &{} \frac{1-b^2}{b^2} &{} 0\\ 0&{}0&{}-1\end{array}\right) \end{aligned}$$
(9)

The reason we have decided to write \(\lambda _1\) and \(\lambda _2\) as \((1-a^2)/a^2\) and \((1-b^2)/b^2\) is due to the fact that in this case, one of the two connected components of \(\mathcal {C}\) can be parametrized as \((a \cos (s), b \sin (s), \sqrt{1-a^2\cos ^2 (s)-b^2\sin ^2 (s)}\, )\)

Theorem 3.2

Let \(\phi (s,t)=\alpha (s)+\beta (t)\) be a minimal translation surface with \(\alpha \) and \(\beta \) parametrized by arc-length and \(\alpha ,\beta \) are not both planar curves. Then up to a reparametrization, a dilation, and a rigid motion we have that

$$\begin{aligned} \beta (t)= & {} \alpha (t)=\int ^t (a \cos (f(t)), b \sin (f(t)), \nonumber \\&\sqrt{1-a^2\cos ^2 (f(t))-b^2\sin ^2 (f(t))}\, )\ dt, \end{aligned}$$
(10)

where the function f(t) satisfies the differential equation

$$\begin{aligned} f^\prime (t)=\frac{\sqrt{1-a^2\cos ^2 (f(t))-b^2\sin ^2 (f(t))}}{a b}. \end{aligned}$$
(11)

Reciprocally, if f is a solution of (11), the surface \(\phi (s,t)=\beta (s)+\beta (t)\) with \(\beta \) defined as in (10) is minimal.

Proof

By Lemma 3.1, we may assume that \(\beta ^\prime (t)\) satisfies the equation \(\langle \beta ^\prime (t),A\beta ^\prime (t)\rangle =0\) where A is the matrix given in (9). A direct computation concludes that

$$\begin{aligned} \beta ^\prime (t)=\left( a \cos (f(t)), b \sin (f(t)), \sqrt{1-a^2\cos ^2 (f(t))-b^2\sin ^2 (f(t))}\, \right) . \end{aligned}$$

From the proof of Theorem 2.3, we have that if \(\kappa \) and \(\tau \) denote the curvature and the torsion of \(\beta \), respectively, then

$$\begin{aligned} \kappa ^2\tau =-\text{ det }(A)=\frac{(1-a^2)(1-b^2)}{a^2b^2} \end{aligned}$$
(12)

Using the formula of \(\kappa \) and \(\tau \) in terms of \(\beta \) ([2, p. 25]), a direct computation shows that

$$\begin{aligned} \kappa ^2\tau = \langle \beta '(t)\times \beta ''(t),\beta '''(t)\rangle =\frac{ab(1-a^2)(1-b^2)f^\prime (t)^3}{\left( 1-a^2\cos ^2 (f(t))-b^2\sin ^2 (f(t))\right) ^\frac{3}{2}}. \end{aligned}$$

Hence we deduce the ODE (11) that satisfies the function f.

In order to prove that up to a reparametrization we may take \(\alpha (t)=\beta (t)\), we recall the definition of the vector subspaces \(H_1\) and \(H_2\) of \(\mathbb {R}^6\):

$$\begin{aligned} H_1= & {} \text{ span }\{(\alpha ^{\prime \prime }(s)\times \alpha ^{\prime }(s),\alpha ^\prime (s)): s\in I\}. \\ H_2= & {} \text{ span }\{(\beta ^\prime (t),\beta ^\prime (t) \times \beta ^{\prime \prime }(t)): t\in J\}. \end{aligned}$$

If we remember the interpretation of the matrix A with respect to the vector space \(H_2\) given in the proof of Theorem 2.3, we can see that a basis of \(H_2\) is given by the vectors

$$\begin{aligned} \left( 1,0,0,\frac{1-a^2}{a^2},0,0\right) ,\quad \left( 0,1,0,0,\frac{1-b^2}{b^2},0\right) ,\quad (0,0,1,0,0,-1) \end{aligned}$$

By Lemma 2.2 we know that \(H_1\) is the orthogonal complement of \(H_2\) and therefore, a direct verification shows that a basis for \(H_1\) is given by the vectors,

$$\begin{aligned} v_1= & {} \left( -\frac{1-a^2}{a^2},0,0,1,0,0\right) ,\quad v_2=\left( 0,-\frac{1-b^2}{b^2},0,0,1,0\right) ,\\ v_3= & {} (0,0,-1,0,0,1) \end{aligned}$$

By the definition of \(H_1\) we obtain that \((\alpha ^{\prime \prime }(s)\times \alpha ^{\prime }(s),\alpha ^\prime (s))=\sum _{i=1}^3\xi _i(s)v_i\), which implies that \((\xi _1(s),\xi _2(s),\xi _3(s))=\alpha ^\prime (s)\) and \(\alpha ^{\prime }(s)\times \alpha ^{\prime \prime }(s)=A\alpha ^\prime (s)\). An important observation that we have deduced here is that the matrix that works for the curve \(\beta \) also works for the curve \(\alpha \). The same argument made above shows that \(\alpha ^\prime (s)\) can be written in the same form as we wrote the curve \(\beta ^\prime (t)\). Notice that by considering the curve \(\tilde{\alpha }(s)=\alpha (-s)\) if necessary, we can assume that \(\alpha ^\prime (s)\) and \(\beta ^\prime (s)\) lie in the same component of \(\mathcal {C}\). Then by considering the curve \(\tilde{\alpha }(s)=\alpha (s+m)\) if necessary, for some \(m\in \mathbb {R}\), we may assume that \(\alpha (s)=\beta (s)\).

To prove the converse, it is immediate that a direct computation shows that the surface parametrized by \(\phi (s,t)=\beta (s)+\beta (t)\) is minimal when \(\beta (t)\) is defined as in (10) and f(t) satisfies Eq. (11). \(\square \)

Remark

The differential equation (11) for f given in Theorem 3.2 can be solved by separation of variables and defines a periodic smooth function in the whole real line. Also, we have that if \(\beta (t)\) is a non-planar curve in \(\mathbb {R}^3\) parametrized by the arc-length, and there exists an invertible symmetric matrix A such that \(\beta ^\prime (t)\times \beta ^{\prime \prime }(t)=A\beta ^\prime (t)\), then \(\phi (s,t)=\beta (s)+\beta (t)\) parametrizes a minimal surface. We can see this by noticing, using Eq. (2), that this surface is minimal if

$$\begin{aligned} \langle \beta ''(s)\times \beta '(s),\beta '(t)\rangle +\langle \beta '(s),\beta '(t)\times \beta ''(t)\rangle =0. \end{aligned}$$

Since \(\beta ^\prime (t)\times \beta ^{\prime \prime }(t)=A\beta ^\prime (t)\), this equation becomes

$$\begin{aligned} \quad -\langle A\beta '(s),\beta '(t)\rangle +\langle \beta '(s),A\beta '(t)\rangle =0, \end{aligned}$$

which holds trivially because A is a symmetric matrix.

The following corollary shows that we can see Theorem 3.2 as a converse result of Theorem 2.3.

Corollary 3.3

If \(\beta =\beta (t)\) is a regular non-planar curve such that \(\kappa ^2\tau =C\) and \(\beta ^\prime (t)\) lies in a cone of the form \(\{x\in \mathbb {R}^3 :\langle Ax,x\rangle =0\}\), then \(\phi (s,t)=\beta (s)+\beta (t)\) defines a minimal surface.

Proof

Let \(\tilde{\beta }\) be a reparametrization of \(\beta \) by arc-length. It is clear that the derivative of the new curve \(\tilde{\beta }\) also lies in the cone \(\{x\in \mathbb {R}^3 :\langle Ax,x\rangle =0\}\). Also, by changing A by \(\lambda A\) for some non-zero \(\lambda \) if necessary, we can assume that \(C=-\hbox {det}(A)\). The corollary follows because, as pointed out in the proof of Theorem 3.2, the equation \(\kappa ^2\tau =-\hbox {det}(A)\) and that \(\tilde{\beta }^\prime (t)\) lies in the intersection of the cone \(\{x\in \mathbb {R}^3:\langle Ax, x\rangle =0\}\) with the sphere \({\mathbb {S}}^2\), implies that up to a rigid motion, a reparametrization and a dilation, \(\tilde{\beta }\) has the form \(\int (a \cos (f(t)), b \sin (f(t)), \sqrt{1-a^2\cos ^2 (f(t))-b^2\sin ^2 (f(t))}\, )\, dt\), where f(t) satisfies the differential equation \(f^\prime (t)= \sqrt{1-a^2\cos ^2 (f(t))-b^2\sin ^2 (f(t))}/(a b) \) for some real numbers a and b. Therefore \(\tilde{\beta }(s)+\tilde{\beta }(t)\) is a minimal surface, as well as \(\beta (s)+\beta (t)\) \(\square \)

From Theorem 3.2, we know that the generators of a minimal translation surface satisfy \(\kappa ^2\tau =C\) for some constant C. First examples of such curves are those curves where \(\kappa \) and \(\tau \) are both constant, which are called circular helices. For any circular helix \(\beta (t)\), a direct computation shows that the vector \(\beta ^\prime (t)\) lies in a circular cone which clearly, up to a rigid motion, can be described as \(\{x\in {\mathbb {R}}^3:\langle Ax, x\rangle =0\}\) where A is a matrix of the form (9) with \(a=b\). Therefore, by Corollary 3.3 and Theorem 3.2 we obtain:

Corollary 3.4

Let \(\beta =\beta (s)\) be a circular helix. Then the surface \(\phi (s,t)=\beta (s)+\beta (t)\) is minimal. Moreover, if \(\phi (s,t)=\alpha (s)+\beta (t)\) is a minimal surface, then up to a rigid motion, a dilation, and a reparametrization, we have that \(\alpha (s)=\beta (s)\). The surface in this corollary is a helicoid.

Notice that the last statement in the corollary was proved in the Introduction of this article. Let us double check that as pointed out in the previous corollary, surfaces in Theorem 3.2 with \(a=b\) are helicoids: in the case that \(a=b\), then Eq. (11) reduces into \(f'(t)=\pm \sqrt{1-a^2}/a^2\). The solution is \(f(t)=\lambda t+\mu \), with \(\lambda =\pm \sqrt{1-a^2}/a^2\) and \(\mu \in \mathbb {R}\). Then

$$\begin{aligned} \beta '(t)=(a\cos (\lambda t+\mu ),a\sin (\lambda t+\mu ), \lambda ). \end{aligned}$$

Up to a constant of integration, the curve \(\beta \) is

$$\begin{aligned} \beta (t)=\frac{1}{\lambda }\left( a\sin (\lambda t+\mu ),-a\cos (\lambda t+\mu ),\lambda ^2 t\right) . \end{aligned}$$

This curve is a circular helix of radius \(a/(1-a^2)^{1/4}\) and pitch \(\sqrt{1-a^2}/a^2\) and we know by Corollary 3.4 that the surface is a helicoid.

Fig. 1
figure 1

The curvature \(\kappa \) (left) and the torsion \(\tau \) (right) of the curve \(\beta (t)\) for values \(a=2/3\) and \(b=1/2\) in Theorem 3.2

Full size image
Fig. 2
figure 2

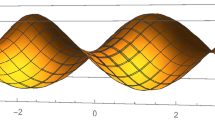
Consider the values \(a=2/3\) and \(b=1/2\) in Theorem 3.2. Left the generator curve \(\beta (t)\); right the minimal translation surface \(\phi (s,t)=\beta (s)+\beta (t)\)

Full size image

To finish this paper, we give a numerical example of a minimal translation surface whose generators are not helices. Consider \(a=2/3\) and \(b=1/2\) in Theorem 3.2. Here the constant C in \(\kappa ^2\tau \) is \(C=15/4\). Given an initial value \( f(0)=0\), we find a solution of

$$\begin{aligned} \left\{ \begin{array}{ll} f^\prime (t)=3 \sqrt{1-\frac{4}{9} \cos ^2{f(t)}-\frac{1}{4}\sin ^2{f(t)}}&{} \\ f(0)=0&{}\end{array}\right. \end{aligned}$$

In Figure 1, we plot the curvature \(\kappa \) and the torsion of the curve \(\beta \) obtained in (10) showing that neither \(\kappa \) nor \(\tau \) is a constant. In Figure 2, we plot the generator curve \(\beta \) with initial condition \(\beta (0)=(2,1,0)\) and the translation surface \(\phi (s,t)=\beta (s)+\beta (t)\).