Introduction

Thermocapillary convection has drawn attentions of researchers in the past few decades and is explored with the in-depth study. Schwabe et al. (1992) used shadowgraph technique to observe the transition from the steady multicellular flow to time-dependent flow in an annular pool with the increase of Marangoni (Ma) number. Garnier et al. (2006) compared the experimental results of annular pools and verified that the azimuthal propagation directions of the hydrothermal waves are opposite when different cylinders (inner or outer cylinder) are heated. Bach and Schwabe (2015) confirmed the existence of surface waves and found that the hydrothermal waves and surfaces waves can coexist. Duan et al. (2018) conducted the experiments of buoyant-thermocapillary convection in annular layers and found three types of transition routes. Meanwhile, a large body of researches shows that thermocapillary convection is closely related to industrial processes. For example, Lappa (2005) and Haslavsky et al. (2011) studied the effect of operating parameters on the melt convection in crystal growth, Cordero et al. (2008) and Motosuke et al. (2012) used thermocapillary convection to manipulate the formation of droplets in microfluidic chips, Davalos-Orozco (2019) and Ding et al. (2019) found thermocapillary flow has effects on the process of film coating.

So far the researches on the thermocapillary convection of low Prandtl (Pr) number fluids were mainly concentrated on theoretical analysis and numerical simulations due to the control difficulty and the precision requirement of experimental measurements. Azami et al. (2001) explored the flow patterns on the free surface of silicon melt in both shallow and deep Czochralski pools. An oblique spoke pattern was observed and the influence of vertical magnetic field on the flow pattern was discussed. Li et al. (2007, 2009) presented the stability characteristics and bifurcations of the thermocapillary flow of a low Prandtl number fluid in annular pools heated from its outer cylinder with linear stability analysis and direct numerical simulations. Shvarts (2012) focused on the instability of the thermocapillary flow in an incompressible fluid layer under micro-gravity condition. The results indicated that the rotation would destabilize the thermocapillary convection first, and then stabilize the transition with the increase of the rotation rate for the fluid of Pr = 0.1. Yin et al. (2016) used Legendre spectral element method to complete the linear stability analysis on thermocapillary flow in the shallow annular pool heated from its outer cylinder. The results revealed that thermocapillary force is a main factor affecting the flow destabilization when the rotation rate is small. Tian et al. (2019) dealt with the thermocapillary convection of silicon melt (Pr = 0.011) in an annular pool heated from its inner wall and found the interaction of thermocapillary force and pool rotational motion would cause particular bifurcation points in a narrow range of rotation rate.

In addition, surface heat dissipation is inevitable when a tangential temperature gradient is applied, which often couples with the flow in the liquid pool. Hoyas et al. (2013) and Torregrosa et al. (2015) conducted a linear stability analysis to explore the effect of Biot number (Bi) and Prandtl number on Marangoni convection in annular pools. It was found that different bifurcations appears and are influenced by Biot number apparently for the fluid with low Prandtl number. Saenz et al. (2013, 2014) numerically investigated the thermocapillary convection in planar liquid layers. It was found that the local heat flux on the free surface has an impact on the hydrothermal waves (HTWs) and the heat absorption restrains HTWs significantly in the evaporation process of the working fluid. Meanwhile, Qin et al. (2014) excavated the effect of heat transfer and phase change on buoyancy-thermocapillary convection in a rectangular pool. They indicated that the vapor diffusion inhabits phase change and affects the flow in both fluid and gas layers. Li et al. (2014) carried out the experiments and linear stability analysis on buoyancy-thermocapillary flow for low-viscosity silicone oil and pointed out that the critical Marangoni number (Macri) of flow destabilization increases with the decrease of the molar fractions of air. Lim and Hung (2015), and Lim et al. (2017) considered the interaction of the surface evaporation and thermocapillary convection in thin liquid films. The results revealed that heat exchange is overestimated when the thermocapillary convection in evaporating liquid films is neglected, and the deviation increases with the increase of temperature. Shi et al. (2016) performed the experiments on Marangoni flow caused by evaporation in an open rectangular cavity. It was found that the HTWs would occur in a small Marangoni number when the evaporation is enhanced. Kozhevnikov and Sheremet (2017) analyzed Marangoni convection with surface evaporation in a cylindrical pool specified non-uniform heat flux along the radial direction. It was shown that the rate of heat transfer decreases with the increase of Marangoni number on the free surface. Grigoriev and Qin (2018) presented the analysis results about the influence of phase change on Marangoni flow in the rectangular pool. They concluded that the temperature fluctuation at the interface is weakened by both heat and mass transfer, which means that there is a stabilization effect on the flow transition in the pool.

Although thermocapillary convection in annular pools was widely studied, little cases about the annular pool heated from its outer cylinder were considered in most of works. Furthermore, the effect of surface heat dissipation deserves further investigation in the annular pool with a heated inner cylinder. This paper presented a series of numerical simulations on the thermocapillary convection of silicon melt (Pr = 0.011) in an annular pool heated from its inner cylinder when the heat dissipation is considered on the free surface. The critical parameters of flow destabilization were determined and the destabilizing mechanism was discussed. In addition, the surface pattern evolution with Marangoni and Biot numbers in the annular pool heated from the inner cylinder was also revealed and the effect of heat dissipation was explained, which compared with the results for annular pool with a heated outer cylinder.

Problem Description and Formulation

Physical Model

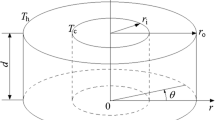
Thermocapillary convection occurs in an annular pool with a rigid bottom, as seen in Fig. 1. The radii of inner and outer cylindrical walls, and the depth of the pool are ri = 20 mm, ro = 40 mm and d = 2 mm, respectively. The radius ratio and the aspect ratio are defined as η = ri/ro = 0.5 and ε = d/(ro − ri) = 0.1. The inner and outer cylinders are maintained at constant temperatures Ti and To (Ti > To). There exists heat dissipation between the free surface and the surrounding with the temperature To. The silicon melt is regarded as a Newtonian fluid and filled in the annular pool whose physical properties are listed in Table 1. The contact angle of the silicon melt on the solid walls is set as 90° and the free surface should be flat and non-deformable at ε = 0.1 (Li et al. 2009; Huang and Zhang 2017; Liu et al. 2019a). Furthermore, the dynamic Bond (Bo) number is introduced to demonstrate the reasonability of buoyancy being ignored. It is defined as Bo = ρgβTd2/γT = 0.21. It means that the buoyancy effect is negligible in this annular pool. Here, ρ is density, βT is thermal expansion coefficient and γT is surface tension temperature coefficient.

Fig. 1
figure 1

Annular pool with surface heat dissipation

Full size image
Table 1 Physical properties of silicon melt at T = 1683 K
Full size table

Mathematical Description

Taking (ro-ri), ν/(ro-ri), (ro-ri)2/ν and νμ/(ro-ri)2 as characteristic scales for length, velocity, time and pressure, respectively, the non-dimensional governing equations of thermocapillary convection can be expressed as the follows

$$ \nabla \cdot V=0 $$
(1)
$$ \frac{\partial V}{\partial \tau }+V\cdot \nabla V=-\nabla P+{\nabla}^2V $$
(2)
$$ \frac{\mathrm{\partial \Theta }}{\partial \tau }+V\cdot \nabla \Theta =\frac{1}{\mathit{\Pr}}{\nabla}^2\Theta $$
(3)

Here, Θ is dimensionless temperature defined by Θ = (T − To)/(Ti − To). V presents dimensionless velocity vector. P and τ are respectively dimensionless pressure and time.

At the initial time, the silicon melt in the annular pool is assumed to be motionless and the temperature distribution is conductive. Thus, the dimensionless initial conditions can be represented as

$$ \tau =0,U=V=W=0,\Theta =\frac{\ln \left[R\left(1-\eta \right)\right]}{\ln \eta } $$
(4a-b)

On all solid walls, the no-slip velocity boundary conditions are specified. On the free surface, the thermocapillary force should be equivalent to the shear stress of silicon melt and the axial velocity is zero. Therefore, we have

$$ \frac{\partial U}{\partial Z}=-\frac{Ma}{\mathit{\Pr}}\frac{\mathrm{\partial \Theta }}{\partial R},\frac{\partial V}{\partial Z}=-\frac{Ma}{\mathit{\Pr}}\frac{\mathrm{\partial \Theta }}{R\partial \theta },W=0 $$
(5a-c)

In Eq. (5), Marangoni number is defined as

$$ Ma={\gamma}_{\mathrm{T}}\Delta T\left({r}_{\mathrm{o}}-{r}_{\mathrm{i}}\right)/\left(\mu \alpha \right) $$
(6)

Here, μ and α are the dynamic viscosity and thermal diffusivity of silicon melt, respectively.

Meanwhile, the thermal boundary conditions on the inner and outer cylinders can be expressed as

$$ R={R}_1,\Theta =1;\kern0.5em R={R}_0,\Theta =0 $$
(7)

The bottom of the annular pool is regarded as adiabatic, thus

$$ Z=0,\mathrm{\partial \Theta }/\partial Z=0 $$
(8)

Assuming that h is the convective heat transfer coefficient between the free surface and the surrounding, the thermal boundary condition on the free surface can be identified as

$$ -\lambda \partial T/\partial z=h\left(T-{T}_0\right) $$
(9)

where λ is thermal conductivity of silicon melt. The dimensionless expression of Eq. (9) is

$$ -\mathrm{\partial \Theta }/\partial Z= Bi\Theta $$
(10)

Here, Bi presents Biot number which is defined as Bi = h(ro-ri)/λ.

Numerical Procedures and Validations

In order to discretize the dimensionless governing equations with particular boundary conditions, the finite volume method is adopted. The central difference approximation is introduced for the diffusion terms while the QUICK scheme is used for the convective terms in both momentum and energy equations. The SIMPLE algorithm is applied for the correction of the pressure-velocity coupling simultaneously. The dimensionless time step ranges from 7.0 × 10−6 to 1.3 × 10−5 for different control parameters. The solution is taken as convergence when the maximum relative error of all governing equations among the computational domains gets below 10−5 at each iteration step.

To describe thermocapillary convection accurately, the non-uniform staggered grid of 80R × 30Z × 200θ with relatively denser meshes close to both the free surface and the rigid walls was used. The mesh convergence is confirmed by simulating the thermocapillary convection under different mesh numbers at Bi = 0 and Ma = 3.0 × 105 in the annular pool with the heated inner cylinder. The results are presented in Table 2. It shows that the wave number m is same and the circumferential average surface temperatures are very close. Thus, the grid of 80R × 30Z × 200θ is chosen for the sake of calculation precision and simulation efficiency.

Table 2 Grid independence check
Full size table

In order to ensure the validity of simulation method, the simulations on the cases given by the previous works (Li et al. 2008, 2009; Yin et al. 2016; Liu et al. 2018, 2019a) were completed and the results are listed in Table 3. Compared with results of the annular pool with a heated outer cylinder (Li et al. 2008, 2009; Yin et al. 2016), the critical wave number (mcri) is same and the maximum deviation of critical Marangoni number is within 8%. Meanwhile, we obtained the critical conditions for low Prandtl fluid in the annular pool with a heated inner cylinder at ε = 0.375. The Prandtl numbers of the fluids are Pr = 0.011 (Liu et al. 2019a) and Pr = 0.01 (Liu et al. 2018), respectively. It can be seen that mcri is same and Macri is a little larger than the results of Liu et al. (2018, 2019a). These numerical results confirm that the method is accurate enough to explore thermocapillary convection in the annular pool heated from the inner cylinder.

Table 3 Calculation for method validation
Full size table

The variation ranges of the main dimensionless parameters in this work are listed in Table 4.

Table 4 Ranges of dimensionless parameters
Full size table

Results and Discussion

Basic Flow and Critical Conditions

As soon as a radial temperature gradient is applied on the free surface, the thermocapillary force begins to drive the fluid flow from the inner cylinder to the outer cylinder on the free surface. When Marangoni number is small, the flow is two-dimensional steady and called as basic flow. In order to describe the velocity field in the annular pool, a dimensionless stream function ψ is introduced and defined as

$$ U=-\frac{1}{R}\frac{\partial \psi }{\partial Z},W=\frac{1}{R}\frac{\partial \psi }{\partial R} $$
(11a-b)

Figure 2 gives the isotherms and streamlines in the annular pool with different heated cylinders at Ma = 1.5 × 103 when Biot number varies from 0 to 0.5. Except near the inner cylinder, as seen in Fig. 2(a), the isotherms are oblique and parallel when the free surface is adiabatic. With the increase of Biot number, the isotherms near the hot inner cylinder are strongly compressed, the absolute value of the maximum dimensionless stream function deceases from 78.82 at Bi = 0 to 66.61 at Bi = 0.5. It means that the basic flow is weakened monotonically by the heat dissipation when the pool is heated from the inner cylindrical wall. It is quite different from the result in the case of the heated outer cylinder (Zhang et al. 2017). Meanwhile, the central position of the main roll cell is always kept near the cold outer cylinder as Biot number is increased. Compared with that in the case of the heated outer cylinder at Bi = 0.5, the isotherms are sparser near the hot inner cylinder while the absolute value of the maximum dimensionless stream function is large in the annular pool heated from its inner cylinder, as seen in Fig. 2(c-d).

Fig. 2
figure 2

Isotherms (up) and streamlines (down) on meridional plane in the annular pool at Ma = 1.5 × 103 for different heated cylinders when Biot number varies from 0 to 0.5. δΘ = 0.05, δψ = 6.1. (a-c) heated from inner cylinder; (d) heated from outer cylinder

Full size image

With the further increase of Marangoni number, the basic flow will destabilize and the unique temperature fluctuations begin to emerge on the free surface. It should be note that the destabilization first occurs near the cold outer cylinder, which is consist with that of the linear stability analysis on the pool heated from its inner cylinder (Liu et al. 2018, 2019b; Tian et al. 2019). For low Prandtl number fluids, the instability also first appears near the cold cylinder when the annular pool is heated from its outer cylinder with adiabatic surface (Li et al. 2007; Yin et al. 2016; Zhang et al. 2017). In order to describe the features of the flow pattern on the free surface, the temperature fluctuation parameter is introduced as follows

$$ \delta \Theta =\Theta \left(R,\varepsilon, \theta, \tau \right)-\frac{1}{2\pi }{\int}_0^{2\pi}\Theta \left(R,\varepsilon, \theta, \tau \right) d\theta $$
(12)

Figure 3(a) shows the critical Marangoni numbers and wave numbers when Biot number ranges from 0 to 1. It can be seen that the critical Marangoni number and critical wave number are Macri = 2.5 × 103 and mcri = 10 respectively when the free surface is adiabatic (Bi = 0). This critical Marangoni number is very close to Macri = 2.61 × 103 obtained with linear stability analysis in the work of Tian et al. (2019) at ε = 0.086 when the free surface is adiabatic. Liu et al. (2019a) have verified that the critical Marangoni number decreases with the increase of the aspect ratio for the fluid of Pr = 0.011 in the annular pools with the heated inner cylinder. However, this result is much higher than the values in the annular pool with a heated outer cylinder and an adiabatic surface, they are Macri = 1.02 × 103 in Yin et al. (2016) and Macri = 1.08 × 103 in Zhang et al. (2017), as marked in Fig. 3(a). A large difference of critical Marangoni number in annular pools with different heated cylinders also has been found in Tian et al. (2019) when Pr = 0.011.

Fig. 3
figure 3

Dependence of Macri (solid symbols) and mcri (hollow symbol) on Biot number (a), and distributions of dimensionless radial velocity (dash lines) on the free surface and temperature differences between the free surface and the bottom (solid lines) when Ma = 1.5 × 103 at different Biot numbers (b)

Full size image

It can be seen that the critical Marangoni number increases monotonically with the increase of Biot number in Fig. 3(a), which is different from the variation tendency in the pool with a heated outer cylinder when the heat dissipation is considered (Zhang et al. 2017). Based on the energy analysis, Tian et al. (2019) and Liu et al. (2018, 2019a) revealed that the main energy for flow destabilization comes from the coaction of the extreme gradients of the radial velocity and temperature distribution near the cold outer cylinder. Figure 3(b) gives the distributions of the dimensionless radial velocity U on the free surface and the dimensionless temperature differences (Θt − Θb) between the free surface and the bottom when Ma = 1.5 × 103 at different Biot numbers. With the increase of Biot number, it is clear that the temperature difference becomes smaller and the radial velocity distribution becomes smoother near the outer cylinder, which means that the energy transfer from the basic flow to the potential perturbations is impaired. Furthermore, the critical wave number keeps constant at mcri = 10 when Bi < 1 and has a slight increase to mcri = 11 until Bi = 1.

Flow Instability and Secondary Transition

When Marangoni number exceeds the critical value, the two-dimensional basic flow would transit to a three-dimensional flow. According to the simulation results at all Biot numbers, it can be found that the two-dimensional basic flow evolves into three-dimensional steady flow first which presents a pairs of longitudinal stationary stripes, and then transits to a three-dimensional oscillatory flow featured with a combination of longitudinal stationary stripes and azimuthal waves on the free surface with the increase of Marangoni number.

When the free surface is adiabatic, the thermocapillary convection after flow destabilization in the annular pool with a heated inner cylinder is different from that with a heated outer cylinder (Zhang et al. 2017). Figure 4 presents the snapshots of the temperature fluctuation and the space-time diagram (STD) of temperature at R = 1.5 on the free surface at Bi = 0. Once Marangoni number exceeds the critical value, the radial stationary stripes emerge on the free surface and the wave number is m = 10 at Ma = 3.0 × 103. The STD at R = 1.5 on the free surface is the regular alternations of white and black vertical stripes without azimuthal movement, which belongs to three-dimensional steady flow (Hoyas et al. 2013; Torregrosa et al. 2015; Liu et al. 2019a). As seen in Fig. 4(a), the stationary stripes almost have occupied the whole free surface. It is quite different from that in the annular pool with a heated outer cylinder. When the free surface is adiabatic and the outer cylinder is heated, the hydrothermal waves immediately appears once the thermocapillary convection destabilizes (Li et al. 2007; Yin et al. 2016). When Ma = 4.0 × 103, as shown in Fig. 4(b), the surface fluctuation indicates that the temperature near the hot inner cylinder has little deformation and the wave number decreases to m = 5. The STD at R = 1.5 shows that the width of the vertical strips varies with the dimensionless time, and the time series of the temperature and velocity at the monitoring point A (R = 1.5, Z = 0.1, θ = 0) presents a strong regularity in Fig. 5(a). It manifests that the flow has transited into a three-dimensional oscillatory flow which could be considered as the combination of radial stationary stripes and azimuthal waves. With the continuously increase of Marangoni number, a secondary instability transition has also been found by Zhang et al. (2017) in the annular pool with an adiabatic surface and a heated outer cylinder. In this case, the radial stationary rolls turn into a combination of the stationary rolls and hydrothermal waves with spiral movement along the azimuthal direction. When Marangoni number further increases to Ma = 4.5 × 103, the time dependencies of the dimensionless temperature and velocity become more complicated. It should be noted that the amplitude of temperature fluctuation on the free surface increases significantly with the increase of Marangoni number.

Fig. 4
figure 4

Temperature fluctuation (up) and the STD at R = 1.5 (down) on the surface at Bi = 0

Full size image
Fig. 5
figure 5

Time series of dimensionless velocity (dotted line) and temperature (solid line) at the monitoring point A (R = 1.5, Z = 0.1, θ = 0) when Bi = 0

Full size image

Figure 6 shows the snapshots of the temperature fluctuation on the free surface and space-time diagram (STD) of temperature at θ = 0 and R = 1.5 at various Marangoni numbers when Bi = 0.5. At Ma = 3.25 × 103, the temperature fluctuation presents regular stationary stripes along radial direction and the STD at R = 1.5 features with regular alternation of the vertical stripes, namely three-dimensional steady flow. The wave number is m = 10. Compared with that at Ma = 3.0 × 103 and Bi = 0 (Fig. 4(a)), the amplitude of temperature fluctuation decreases even if Marangoni number increases from Ma = 3.0 × 103 to 3.25 × 103, which indicates that the heat dissipation could weaken the temperature fluctuation apparently on the free surface. The STD at θ = 0 shows that the temperature is continuous and unchanging, which confirms that there is no azimuthal motion of the temperature fluctuation on the free surface. However, the thermocapillary convection has been changed into a three-dimensional oscillatory flow at Ma = 3.5 × 103. As shown in Fig. 6(b), although the temperature fluctuation on the free surface still presents distinct high and low temperature regions with longitudinal rolls, the STD at R = 1.5 clearly shows that there are local oscillations with azimuthal movement in each stripe. The STD at θ = 0 illustrates that the alternation of temperature fluctuations exists in the radial direction, which is quite different from that at Ma = 3.25 × 103. Furthermore, Fig. 7 gives the time series of temperature and velocity, and the frequency spectrum of dimensionless temperature variation at point A (R = 1.5, Z = 0.1, θ = 0). It can be seen that the temperature and velocity presents regular oscillations at Ma = 3.5 × 103 whose fundamental frequency is F1 = 500.29. When Marangoni number reaches at Ma = 5.0 × 103, although the temperature fluctuation shows that the whole free surface is divided into nine parts along azimuthal direction, the time series of temperature and velocity and the frequency spectrum of dimensionless temperature indicate that the thermocapillary convection has turned into chaotic flow. The STD both at θ = 0 and R = 1.5 also shows the strong irregularity.

Fig. 6
figure 6

Temperature fluctuation (left) on the free surface and the STD at θ = 0 (middle) and R = 1.5 (right) when Bi = 0.5

Full size image
Fig. 7
figure 7

Time series of dimensionless velocity (dotted line) and temperature (solid line) (left)and frequency spectrum of temperature (right) at the monitoring point A (R = 1.5, Z = 0.1, θ = 0) when Bi = 0.5

Full size image

Compared with that at Bi = 0, the secondary instability transition from the radial stationary stripes to the three-dimensional oscillatory flow is more obvious at Bi = 0.5. Almost the same transition has also been observed in the experiment of Burguete et al. (2001). The given spatiotemporal evolution of the three-dimensional oscillatory flow in Fig. 17 of Burguete et al. (2001) is similar to those in Fig. 6(b) and 6(c). Furthermore, the evolution of the surface pattern with Marangoni number is quite different from that in the annular pool with a heated outer cylinder. Zhang et al. (2017) reported that with the increase of Marangoni number, a three-dimensional steady flow occurs first and then directly evolves into the hydrothermal waves when the outer cylinder of the pool is heated and surface heat dissipation is considered.

The secondary instability transition can be explained as follows. Figure 8 gives the snapshots of temperature fluctuation, the STD at R = 1.5 on the free surface, the partial enlargement of the temperature fluctuation on the free surface and the temperature fluctuation on the meridional plane at θ = 0 during one period at Ma = 4.0 × 103. When Marangoni number reaches Ma = 4.0 × 103, the wave number keeps m = 10, the temperature fluctuation becomes more intense and the movement of the local oscillations presents more vigorous on the free surface, as shown in Fig. 8. Assuming that the local distribution of temperature fluctuation on the free surface is labeled at Fig. 8(a), the fluid temperature at point “a” is higher than that at point “b”, causing the fluid flow from point “a” to point “b” and carrying the heat simultaneously. In addition, the radial convection of the fluid from the hot inner cylinder to the cold outer cylinder would be strengthened to supply the heat and fluid dispersal near the point “a”. The temperature fluctuation on the meridional plane at θ = 0 manifests that the radial convection always maintains a high temperature in most region of the free surface and keeps the distinct high and low temperature regions on the surface during a period. The low temperature region near the inner hot cylinder is caused by the strong effect of heat dissipation on the free surface (Qin et al. 2014). The fluid accumulation with high temperature makes the temperature near point “b” gradually rise and the temperature increment be inconsistent along the radial direction because of the occurrence of the local azimuthal convection both in clockwise and counterclockwise direction simultaneously. As seen in Fig. 8(b), for the point “b” in the counterclockwise direction of the point “a”, the temperature close to the hot inner cylinder increases and the temperature in the middle of pool decreases. The temperature decrease in the middle of pool will induce a stronger azimuthal flow from point “a”, which carries heat and then increases the temperature, as seen in Fig. 8(c). It means that the local temperature distribution will be further changed by the continuous azimuthal convection. Meanwhile, the increase of temperature would be reduced by the surface heat dissipation synchronously. Therefore, the unique secondary instability transition is caused by the coupling of the radial convection, local azimuthal flow and heat dissipation, which presents a coupling of the radial stationary rolls and azimuthal waves.

Fig. 8
figure 8

Mechanism of secondary instability transition at Bi = 0.5 and Ma = 4.0 × 103. The temperature fluctuation on the surface and STD at R = 1.5 (up), and the partial enlargement of temperature fluctuation on the free surface (middle) and the corresponding temperature fluctuation on the meridional plane (down) at θ = 0 during one period

Full size image

Effect of Biot Number

The heat dissipation can change the flow pattern significantly at a fixed Marangoni number. When Marangoni number just exceeds the critical value, the temperature fluctuation presents longitudinal stationary rolls on the free surface. Figure 9 gives the temperature fluctuation on the free surface and the STD at R = 1.5 when Ma = 3.0 × 103 and Bi = 0.3. It can be seen that the STD is vertical stripes and the wave number m = 10 at Bi = 0.3. Combined with the surface pattern at Bi = 0 at Ma = 3.0 × 103 (Fig. 4(a)), the amplitude of temperature fluctuation decreases with the increase of Biot number and the wave number decreases slightly from m = 10 at Bi = 0 to m = 9 at Bi = 0.3. The thermocapillary flow still presents a basic flow without any temperature fluctuation at Ma = 3.0 × 103 at Bi = 0.5. It means that the heat dissipation suppresses the flow destabilization in the annular pool when Marangoni number is small.

Fig. 9
figure 9

Temperature fluctuation (left) on the free surface and the STD at R = 1.5 (right) when Ma = 3.0 × 103 and Bi = 0.3

Full size image

With the increase of Marangoni number, the effect of heat dissipation is more special. Figure 10 gives the snapshots of temperature fluctuation on the free surface and the STD at R = 1.5, and the frequency spectrum of temperature fluctuation at the monitoring point A (R = 1.5, Z = 0.1, θ = 0) when Ma = 4.5 × 103. As shown in Fig. 4(c), when the free surface is adiabatic, the temperature fluctuation presents a series of distinct black and white vertical stripes and the wave number m = 5. The temperature fluctuation becomes more irregular when the heat dissipation is considered on the free surface, as seen in Figs. 10(a) and (b). It can be found that the wave number increases with the increase of Biot number. Based on the STD at R = 1.5, the temperature fluctuation at Bi = 0.5 is made up of two staggered groups of azimuthal waves with a phase difference. The frequency spectrum shows that the fundamental frequency is F1 = 548.78 with a harmonic frequency of F2 = 149.47. When Bi = 1, the temperature fluctuation shows the alternating radial waves, the STD indicates that the alternation is aroused by the continuous oblique stripes with the dimensionless time, which is asynchronous in azimuthal direction. Meanwhile, there is just one main peak with F1 = 99.65 in the frequency spectrum of temperature fluctuation, which suggests that the movement of radial stripes becomes faster at Bi = 1.

Fig. 10
figure 10

Snapshots of temperature fluctuation (left) on the free surface, the STD at R = 1.5 (middle) and the frequency spectrum of temperature fluctuation (right) at the monitoring point A (R = 1.5, Z = 0.1, θ = 0) when Ma = 4.5 × 103 for different Biot numbers

Full size image

Conclusions

The numerical simulations of thermocapillary convection in an annular pool with surface heat dissipation and a heated inner cylinder are performed. According to the simulation results, the following conclusions can be drawn.

  1. (1)

    Surface heat dissipation could restrict flow destabilization and change surface pattern for low Prandtl number fluids (Pr = 0.011). Specifically, the isotherms become strongly compressed near the hot inner cylinder.

  2. (2)

    Critical Marangoni number of flow destabilization increases monotonically with the increase of Biot number. After flow destabilization, the amplitude of temperature fluctuation increases and the wave number decreases with the increase of Marangoni number when the free surface is adiabatic.

  3. (3)

    The temperature fluctuations on the free surface and the meridional plane revealed that the secondary instability transition is caused by the mutual effects of the radial convection, azimuthal local flow and heat dissipation.