Introduction

As one of the important issues in the information age, image security has received increasing attention. Among numerous technologies for image encryption, optical technique plays an important role owing to its high computation speed, high parallelism in applications and arbitrary parameter selection. In 1995, double random phase encoding (DRPE) technique in Fourier transform domain was proposed by Refregier and Javidi [1]. After that, DRPE was extended to other transform domains, such as fractional Fourier domain [2] and Fresnel domain [3]. Some other optical image encryption schemes based on joint transform correlators [4], digital holography [5–7], photon counting imaging [8] and compressive sensing [9, 10] were also proposed subsequently. It is worth mentioning that optical image encryption schemes based on DRPE technique can readily be performed using digital holography, owing to its excellent performance in recording and reconstructing the complex values. Phase-shifting techniques, such as four-step [5] and two-step [6] phase shift, are commonly used to retrieve the original complex information in digital holography. Nevertheless, these techniques need at least two interferograms to reconstruct the original complex object field. Unlike phase-shifting techniques, single-shot digital holography [7, 11] needs only one single-frame hologram to retrieve the original complex information.

Obviously, random phase masks play a key role in the optical image encryption schemes based on DRPE technique. When transmitting the encrypted images, effective and convenient management of secret keys is important for the encryption scheme. In most of the existing DRPE-based encryption schemes, the whole random phase masks with the same size as encrypted image have to be sent to the authorized receiver side to decrypt the original image, which is inconvenient for the secret key management and transmission. The majority of previous studies focused on devising optical encryption systems, but few attention was paid to the new random phase encoding techniques.

Recently, the chaos-based encryption technique has become an interesting research topic. This technique can provide a good combination of speed, high security, complexity and computational power [12]. Chaotic maps have many fundamental properties, which can be considered analogous to some cryptographic properties of ideal ciphers, so they are widely used to encrypt digital images. In recent years, researchers have tried to propose some chaotic random phase encoding techniques. An image encryption scheme using fractional Fourier transform and chaos theory was proposed by Singh and Sinha [13], in which the random phase masks are generated by one single chaotic map such as Tent map. A double-image encryption scheme based on discrete multi-parameter fractional angular transform and two-coupled logistic maps was proposed by Sui et al. [14], in which the images are scrambled by two-coupled logistic maps before the optical processing step, and the random phase masks are generated by one single logistic map in the optical processing step. The 1-D single chaotic maps including logistic map and Tent map have the advantages of simplicity and low computational complexity. However, there are some drawbacks such as small key space and weak security [15] existing in the cryptosystem based on these chaotic maps. To avoid these problems, a novel mixed chaotic method is proposed to generate the random phase masks in this paper. In the proposed method, two 1-D single chaotic maps with distinct structures are combined to form a mixed chaotic map, and the two random phase masks are generated by two different mixed chaotic maps, respectively. Based on the chaotic random phase masks, optical image encryption and decryption are realized with a single-shot digital holographic technique. In the proposed encryption scheme, the initial value and parameters of mixed chaotic maps serve as secret keys, which is convenient for the key management and transmission. Moreover, the proposed encryption scheme possesses high resistance against statistical attack, brute-force attack, noise attack and shear attack. Simulation results and security analysis also verify the validity and security of the proposed scheme.

The rest of the paper is organized as follows. In Sect. 2, the construction of mixed chaotic maps will be described in detail. The optical image encryption scheme that combines single-shot digital holography with chaotic random phase masks will be presented in Sect. 3. Security analysis and numerical simulation results are given to verify the security and validity of the proposed encryption scheme in Sect. 4. Finally, conclusions are given in Sect. 5.

Mixed Chaotic Maps

Chaotic maps have many important properties, such as the sensitive dependence on the initial values and system parameters, pseudorandom property, nonperiodicity and topological transitivity. Most of these properties meet requirements such as permutation and diffusion in the sense of cryptography. Therefore, chaotic maps, especially the 1-D single chaotic maps, have more useful and practical applications in image encryption schemes. Though the 1-D single chaotic maps have the advantages of simplicity and low computational complexity, there are some drawbacks such as small key space and weak security existing in the cryptosystems based on these chaotic maps. With the logistic map [16] as an example, when the initial parameters are set as particular values, the security of cryptosystem based on logistic map will become very weak. Figure 1 shows the iterated results of logistic map when the initial parameters are set as \(x_{0} = 0.25,\mu = 4\). One can find that the iterated values are constant, and there are no random sequences generated. In this case, the logistic map cannot be used to encrypt the image. This is not a rare phenomenon in logistic map, but it happens in other 1-D single chaotic maps. Therefore, to avoid these problems, a novel mixed chaotic method is proposed to generate the random phase masks. In the proposed method, two 1-D single chaotic maps with distinct structures are combined to form a mixed chaotic map. The 1-D single chaotic maps used in this paper are chosen as logistic map [16], iterative chaotic map with infinite collapses (ICMIC) map [17] and Chebyshev map [18], respectively.

Fig. 1
figure 1

Iterative results of logistic map

Full size image

The discrete form of logistic map is defined as

$$x_{n + 1} = \mu x_{n} \left( {1 - x_{n} } \right)$$
(1)

When the control parameter \(\mu \in \left( {3.5699,4} \right]\), the logistic map is chaotic.

The discrete form of ICMIC map is defined as

$$x_{n + 1} = \sin \left( {{a \mathord{\left/ {\vphantom {a {x_{n} }}} \right. \kern-0pt} {x_{n} }}} \right)$$
(2)

When the control parameter \(a \in \left( {0,\infty } \right)\), the ICMIC map is chaotic.

The discrete form of Chebyshev map is defined as

$$x_{n + 1} = \cos \left( {w\left( {\cos^{ - 1} x_{n} } \right)} \right)$$
(3)

When the control parameter \(w \in \left[ {2,\infty } \right)\), the Chebyshev map is chaotic.

To construct the first mixed chaotic map, an appropriate initial value is firstly assigned to logistic map. Then, the output value of logistic map is used as the initial value of ICMIC map, and the random number sequence generated by ICMIC map will be used to generate the first random phase mask. The first mixed chaotic map can be written as

$$\left\{ {\begin{array}{*{20}l} {x_{n + 1} = \mu x_{n} \left( {1 - x_{n} } \right)} \hfill \\ {y_{n + 1} = \sin \left( {{a \mathord{\left/ {\vphantom {a {y_{n} }}} \right. \kern-0pt} {y_{n} }}} \right)} \hfill \\ \end{array} } \right.$$
(4)

Similarly, the appropriate initial value is firstly assigned to logistic map, and the output value of logistic map is then used as the initial value of Chebyshev map. The random number sequence generated by Chebyshev map will be used for generating the second random phase mask. The second mixed chaotic map can be written as

$$\left\{ {\begin{array}{*{20}l} {x_{n + 1} = \mu x_{n} \left( {1 - x_{n} } \right)} \hfill \\ {y_{n + 1} = \cos \left( {w\left( {\cos^{ - 1} y_{n} } \right)} \right)} \hfill \\ \end{array} } \right.$$
(5)

The proposed mixed chaotic maps can largely help avoid the problem that 1-D single chaotic maps encounter. In addition, the extended key space of mixed chaotic maps can further increase the security of cryptosystems. In this paper, two random phase masks are, respectively, generated by two different mixed chaotic maps. The chaotic random phase masks can be controlled by the initial value and parameters of mixed chaotic maps, which is convenient for the key transmission and management.

Proposed Optical Image Encryption Scheme

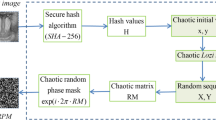
In this section, two chaotic random phase masks are introduced to the optical security system, as shown in Fig. 2. The original image is multiplied by the first chaotic random phase mask (CRPM) represented by \(\exp \left[ {{\text{i}}2\pi c_{1} \left( {x_{0} ,y_{0} } \right)} \right]\), where \(c_{1} \left( {x_{0} ,y_{0} } \right)\) is the random number sequence generated by the first mixed chaotic map. Then, the optical field distribution on the plane \(\left( {x_{1} ,y_{1} } \right)\) can be written as

Fig. 2
figure 2

Optical setup of the proposed cryptosystem. M mirror, L 0 , L lens, SF spatial filter, D diaphragm, BS beam splitter, CCD charge-coupled device

Full size image
$${\text{FrT}}_{{Z_{1} }} \left\{ {U_{0} \left( {x_{0} ,y_{0} } \right)\exp \left[ {{\text{i}}2\pi c_{1} \left( {x_{0} ,y_{0} } \right)} \right]} \right\}$$
(6)

where \({\text{FrT}}_{{Z_{ 1} }}\) is the Fresnel transform of distance \(z_{ 1}\); \(U_{0}\) is the complex value of original image.

This optical field distribution is then encoded by the second CRPM represented by \(\exp \left[ {{\text{i2}}\pi c_{2} \left( {x_{1} ,y_{1} } \right)} \right]\), where \(c_{2} \left( {x_{1} ,y_{1} } \right)\) is the random number sequence generated by the second mixed chaotic map. The optical field distribution on the recording plane \(\left( {x,y} \right)\) can be written as

$$O_{0} \left( {x,y} \right) = {\text{FrT}}_{{Z_{ 2} }} \left\{ {{\text{FrT}}_{{Z_{ 1} }} \left\{ {U_{0} \left( {x_{0} ,y_{0} } \right)\exp \left[ {{\text{i2}}\pi c_{1} \left( {x_{0} ,y_{0} } \right)} \right]} \right\}\exp \left[ {{\text{i2}}\pi c_{2} \left( {x_{1} ,y_{1} } \right)} \right]} \right\}$$
(7)

where \(O_{0}\) is the object wave function on CCD camera plane; \({\text{FrT}}_{{{\text{Z}}_{ 2} }}\) is the Fresnel transform of distance \(z_{ 2}\).

Suppose that the reference wave is expressed as

$$R = \left| R \right|\exp \left( {{\text{i}}kx\sin \theta } \right)$$
(8)

where \(k\) is the wave number; and \(\theta\) is the angle between reference wave and object wave.

The reference wave and object wave intervene on the CCD plane to form a hologram, i.e., a noise-like encrypted image can be expressed as

$$H = \left| {O_{0} } \right|^{2} + \left| R \right|^{2} + R^{ * } O_{0} + O_{0}^{ * } R$$
(9)

where \(*\) stands for a complex conjugate.

To decrypt the original image, the single-shot digital holographic technique is adopted. This technique models the reconstruction of complex object field on the hologram plane as a constrained optimization problem, and the cost function to be minimized can be expressed as

$$C\left( {O,O^{ * } } \right) = \frac{1}{2}\left\| {H - \left( {\left| O \right|^{2} + \left| R \right|^{2} + R^{ * } O + O^{ * } R} \right)} \right\|^{2} + \alpha \psi \left( {O,O^{ * } } \right)$$
(10)

where \(\psi \left( {O,O^{ * } } \right)\) is a penalty function for imposing a smoothness constraint on the complex object function \(O\); and \(\alpha\) is a control parameter. The optimization problem can be solved iteratively by steepest descent method. The gradient of the cost function in Eq. (10) with respect to \(O^{ * }\) may be calculated as

$$\nabla_{{O^{ * } }} C\left( {O,O^{ * } } \right) = - \left[ {H - \left( {\left| O \right|^{2} + \left| R \right|^{2} + R^{ * } O + O^{ * } R} \right)} \right]\left( {O + R} \right) + \alpha {\nabla }_{{O^{ * } }} \psi \left( {O,O^{ * } } \right)$$
(11)

Hence, the iterative solution is

$$\begin{aligned} O^{(n + 1)} & = O^{(n)} - t\left[ {\nabla_{{O^{*} }} C} \right]_{O = O^{(n)}} \\ & = O^{(n)} + t\left[ {H - \left( {\left| {O^{(n)} } \right|^{2} + \left| R \right|^{2} + R^{ * } O^{(n)} + O^{(n)*} R} \right)} \right]\left( {O^{(n)} + R} \right) \\ \end{aligned}$$
(12)

where \(t\) is step size. Operationally, \(\alpha\) is set as zero.

The results of the iterative procedure in Eq. (12) give a complex object function \(O\left( {x,y} \right)\), and then, the original image can be retrieved as

$$U_{0}^{\dag } \left( {x_{0} ,y_{0} } \right) = {\text{IFrT}}_{{Z_{ 1} }} \left\{ {{\text{IFrT}}_{{Z_{ 2} }} \left[ {O\left( {x,y} \right)} \right]\exp \left[ {{{ - \text{i}2}}\pi c_{2} \left( {x_{1} ,y_{1} } \right)} \right]} \right\}\exp \left[ {{{ - \text{i}2}}\pi c_{1} \left( {x_{0} ,y_{0} } \right)} \right]$$
(13)

Security Analysis and Experiment Results

To verify the feasibility and effectiveness of the proposed scheme, numerical simulations are performed on two plain images of “TEST” and “Peppers,” as shown in Fig. 3a, b. In these numerical simulations, the proposed encryption scheme is compared with the method in Ref. [13] in terms of key sensitivity and correlation coefficient analysis of adjacent pixels. The numerical simulations are completed by MATLAB R2011a on a PC with Core i3-2120, 3.3 GHz CPU and 2 GB RAM memory. In the proposed encryption scheme, the initial value and parameters of the mixed chaotic maps are set as \(x_{0} = 0.3141\), \(\mu = 3.8956\), \(a = 12.5098\) and \(w = 4\), and the parameters of the optical system are set as \(\lambda { = 632} . 8 {\text{ nm}}\), \(z_{ 1} {\text{ = 500 mm}}\), \(z_{ 2} {\text{ = 300 mm}}\), \(n = 20\) and \(t = 0.005\), respectively. For the method in Ref. [13], the initial values and parameters of logistic map are set as \(x_{1} = 0.241\), \(\mu_{1} = 3.85\) and \(x_{2} = 0.341\), \(\mu_{2} = 3.96\) to generate the first and second random phase masks, and the fractional orders of the first and second fractional Fourier transform systems are set as \((0.75,0.9)\) and \((1.25,1.1)\), respectively. Figure 3c, d shows the encrypted image of “TEST” and “Peppers,” respectively. The decrypted images with correct keys are shown in Fig. 3e, f, from which one can find that the original image can be retrieved from the encrypted image well.

Fig. 3
figure 3

Two plain images and their encryption and decryption results. a Plain image “TEST,” b plain image “Peppers,” c encrypted image “test,” d encrypted image “peppers,” e decrypted image “test” and f decrypted image “Peppers”

Full size image

Key Space Analysis

The set of all initial values and parameters of mixed chaotic maps compose the main key space. The main key space of the proposed encryption scheme has four secret key values, i.e., \(x_{0} = 0.3141\), \(\mu = 3.8956\), \(a = 12.5098\) and \(w = 4\). As stated in the IEEE floating-point standard, the computational precision of the 64-bit double-precision number is about 10−15. Therefore, the main key space of the proposed encryption scheme is (1015)4 = 1060 ≈ ←2199. Furthermore, the parameters of optical encryption system such as diffraction distance and incident wavelength can also be used as one part of the key size. From the above analysis, one can find that the key space of the proposed encryption scheme is large enough to resist the brute-force attack.

Sensitivity of Keys

In the proposed encryption scheme, the initial value and parameters of mixed chaotic maps serve as the main keys. In Ref. [13], the initial value \(x_{2}\) and parameter \(\mu_{2}\) of logistic map serve as the main keys. To evaluate the key sensitivity, the encryption and decryption are repeated with a tiny alteration introduced to one of the correct keys each time. To demonstrate the difference between the two encrypted images \(C_{1}\) and \(C_{2}\) which are obtained from the same plain image by using two similar encryption keys, the number of pixels change rate (NPCR) and the unified average changing intensity (UACI) are computed. The NPCR and UACI are defined as follows:

$${\text{NPCR = }}\frac{{\sum\nolimits_{i = 0}^{W - 1} {\sum\nolimits_{j = 0}^{H - 1} {D\left( {i,j} \right)} } }}{WH} \times 100\%$$
(14)
$${\text{UACI = }}\frac{1}{WH}\left( {\sum\limits_{i = 0}^{W - 1} {\sum\limits_{j = 0}^{H - 1} {\frac{{\left| {C_{1} \left( {i,j} \right) - C_{2} \left( {i,j} \right)} \right|}}{255}} } } \right) \times 100\%$$
(15)

where \(D\) is a two-dimensional set with the same size as image \(C_{1}\) or \(C_{2}\); \(W\) and \(H\) are the width and height of the image, respectively. The set \(D\left( {i,j} \right)\) is defined by \(C_{1} \left( {i,j} \right)\) and \(C_{2} \left( {i,j} \right)\): if \(C_{1} \left( {i,j} \right) \ne C_{2} \left( {i,j} \right)\) then \(D\left( {i,j} \right) = 1\); otherwise, \(D\left( {i,j} \right) = 0\). The NPCR and UACI test results from the proposed encryption algorithm and the method in Ref. [13] are listed in Table 1. It can be seen that the proposed encryption algorithm is sensitive with respect to small changes of secret keys, and the proposed encryption algorithm outperforms the method in Ref. [13].

Table 1 NPCR and UACI results of the two encrypted images with similar secret keys (k, k*)
Full size table

To demonstrate the difference between the original image \(U_{0}\) and the decrypted image \(U_{0}^{\dag }\) numerically, the correlation coefficient (CC) is calculated as follows

$${\text{CC}} = \frac{{E\left\{ {\left[ {U_{0}^{\dag } - E\left[ {U_{0}^{\dag } } \right]} \right]\left[ {U_{0} - E\left[ {U_{0} } \right]} \right]} \right\}}}{{\sqrt {E\left\{ {\left[ {U_{0}^{\dag } - E\left[ {U_{0}^{\dag } } \right]} \right]^{2} } \right\}E\left\{ {\left[ {U_{0} - E\left[ {U_{0} } \right]} \right]^{2} } \right\}} }}$$
(16)

where \(E\left\{ \cdot \right\}\) is an expectation operator. Note that the higher the value of CC, the smaller the difference between the decrypted and original images.

The images of “TEST” and “Peppers” are decrypted under the condition that one key is incorrect while the other keys are correct, and the decrypted images are shown in Figs. 4 and 5, respectively. Figures 4a–d and 5a–d show the decrypted images “TEST” and “Peppers” by the proposed encryption scheme with incorrect keys \(x_{0}^{\dag } = x_{0} + 1 \times 10^{ - 15}\), \(\mu^{\dag } = \mu + 1 \times 10^{ - 15}\), \(a^{\dag } = a + 1 \times 10^{ - 15}\) and \(w^{\dag } = w + 1 \times 10^{ - 15}\), respectively. These decrypted images with incorrect keys do not show the information about the original images visually. Figures 4e, f and 5e, f show the decrypted images “TEST” and “Peppers” by the method in Ref. [13] with incorrect keys \(x_{2}^{\dag } = x_{2} + 1 \times 10^{ - 15}\) and \(\mu_{2}^{\dag } = \mu_{2} + 1 \times 10^{ - 15}\), respectively. The CC of Figs. 4a–f and 5a–f is 0.0043, 0.0005, 0.0018, 0.0041, 0.0300, 0.0144 and 0.0165, 0.0151, 0.0155, 0.0138, 0.0183, 0.0171, respectively, which means that the proposed encryption scheme outperforms the method in Ref. [13].

Fig. 4
figure 4

Decrypted results of image “TEST” with incorrect keys. a Decrypted image with x 0 + 10−15, b decrypted image with μ + 10−15, c decrypted image with a + 10−15, d decrypted image with w + 10−15, e decrypted image with x 2 + 10−15 and f decrypted image with μ 2 + 10−15

Full size image
Fig. 5
figure 5

Decrypted results of image “Peppers” with incorrect keys. a Decrypted image with x 0 + 10−15, b decrypted image with μ + 10−15, c decrypted image with a + 10−15, d decrypted image with w + 10−15, e decrypted image with x 2 + 10−15 and f decrypted image with μ 2 + 10−15

Full size image

The above results indicate that the proposed encryption scheme is highly sensitive to the secret keys. Even an almost perfect guess of the key does not reveal any valuable information about the plain image. In addition, the results also indicate that the proposed encryption scheme outperforms the method in Ref. [13] in terms of key sensitivity.

Correlation Coefficient Analysis of Adjacent Pixels

In order to test the correlation of adjacent pixels, 1 000 pairs of adjacent pixels are randomly selected in the vertical, horizontal and diagonal directions from the plain images “TEST” and “Peppers” as well as from the corresponding cipher images encrypted by the proposed encryption scheme and the method in Ref. [13]. The correlation coefficient of two adjacent pixels \(\left( {x_{i} ,y_{i} } \right)\) is calculated as

$${\text{Cor}} = \frac{{\text{cov} \left( {x,y} \right)}}{{\sqrt {D\left( x \right)} \sqrt {D\left( y \right)} }}$$
(17)

where

$$D\left( x \right) = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {x_{i} - \bar{x}} \right)^{2} }$$
(18)
$$D\left( y \right) = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {y_{i} - \bar{y}} \right)^{2} }$$
(19)
$$\text{cov} \left( {x,y} \right) = \sum\limits_{i = 1}^{N} {\left( {x_{i} - \bar{x}} \right)} \left( {y_{i} - \bar{y}} \right)$$
(20)

where \(N\) is the total number of couples \(\left( {x_{i} ,y_{i} } \right)\); and \(\bar{x},\begin{array}{*{20}c} {} \\ \end{array} \bar{y}\) are the mean values of \(x_{i}\) and \(y_{i}\), respectively.

Table 2 shows the results of correlation computations of two adjacent pixels in the plain images and the corresponding cipher images encrypted by different encryption methods. It is clear that the two adjacent pixels of the plain images are highly correlated in the three directions. And for the cipher images encrypted by the proposed encryption scheme, there is a negligible correlation between the two adjacent pixels in three directions. In addition, the correlation between two adjacent pixels in the cipher images encrypted by the method in Ref. [13] is higher than those encrypted by the proposed encryption scheme. The results indicate that the proposed encryption scheme outperforms the method in Ref. [13], and the unauthorized users cannot get any valid information from the statistical data.

Table 2 Horizontal, vertical and diagonal correlation coefficients of adjacent pixels in the plain and encrypted images
Full size table

Noise Attack

During the transmission, the encrypted images may be polluted by various types of noises. In order to investigate the performance of the proposed encryption scheme against noise attack, three different kinds of noises, i.e., Gaussian noise with zero mean, salt and pepper noise and speckle noise, are added to the encrypted image of “TEST” by using the imnoise function in MATLAB. Figure 6a–c is the decrypted image of “TEST” retrieved from the encrypted data polluted by Gaussian noise, salt and pepper noise and speckle noise at 0.10 noise level, respectively. And the corresponding values of CC are 0.5938, 0.8748 and 0.9127, respectively. The results demonstrate that the decrypted images can be recognized despite of some noise interference, and the proposed encryption scheme can tolerate a certain range of noise level.

Fig. 6
figure 6

Robustness against noise attacks. a Decrypted image with Gaussian noise, b decrypted image with salt and pepper noise and c decrypted image with speck noise

Full size image

Shear Attack

During the transmission, the encrypted image may also be partially lost. Therefore, the robustness against shear attack should be considered. Figure 7a–c shows the encrypted images of “TEST” damaged by 12.5, 25 and 50%, respectively. The decryption process is performed on these damaged cipher images with all correct keys. The corresponding decrypted results are shown in Fig. 7d–f, from which the main information of the original image can be recognized visually. The CCs of Fig. 7d–f are 0.8612, 0.6409 and 0.2581, respectively, indicating that the proposed encryption scheme has high robustness against the shear attack.

Fig. 7
figure 7

Robustness against shear attacks. a Encrypted image with damaged 12.5%, b encrypted image with damaged 25%, c encrypted image with damaged 50%, d decrypted image from (a), e decrypted image from (b) and f decrypted image from (c)

Full size image

Conclusions

A novel mixed chaotic method for generating the random phase masks is proposed. Based on CRPM, optical image encryption and decryption are realized with a single-shot digital holography. In the proposed optical encryption scheme, the plain images fail to be recovered unless all of the correct keys are known. Moreover, the proposed encryption scheme has high resistance against potential attacks, such as brute-force attack, statistical attack, noise attack and shear attack. In addition, the proposed encryption scheme does not use any phase keys in the encryption and decryption process, which is convenient for the transmission and management of secret keys. Numerical simulations illustrate the feasibility and effectiveness of the proposed encryption scheme.