Introduction

There are currently two lines of thought, namely core accretion and gravitational instability for the formation of solar system planets (Paul et al. 2013). According to the first line of thought, the evolution of the planets starts with the formation of a heavy element core by accretion of planetesimals (Safronov 1969; Lissauer 1993; Pollack et al. 1996; Hubickyj et al. 2005). As this core grows, it begins to accrete the surrounding gas. Once the core reaches a critical mass of 10 M⊕, where M⊕ is the mass of the earth, the rate of gas accretion becomes very high and a Jupiter-mass object is formed (Pollack et al. 1996; Hubickyj et al. 2005). This mechanism has been accepted widely as the standard one of planetary formation in the case of our own solar system as that of the extrasolar ones (see Mizuno 1980; Pollack et al. 1996; Hubickyj et al. 2005; Paul et al. 2012a, 2013). Recently, extrasolar planets are discovered by direct imaging (Marois et al. 2008; Kalas et al. 2008), where the core accretion model cannot be found to explain properly the formation process of such planets, because it is believed that the gas disk surrounding a young star disappears before the formation of the massive solid core (Dodson-Robinson et al. 2009). As in Paul et al. (2012a), with the difficulties encountered in the core accretion models, the disk instability or gravitational instability model, once in vogue, has been reformulated with fragmentation from massive protoplanetary disks (Boss 1998a, b; Nayakshin 2010; Boley et al. 2010; Cha and Nayakshin 2011; Paul et al. 2012a, b, 2013; Paul and Senthilkumar 2016). According to Boss (1998b), the gravitational instability proceeds very quickly, with an unstable disk breaking up into giant gaseous protoplanets. Although some questions arise as to whether stable protoplanets could be formed or not by disk instability, the idea is believed to be a promising route to the rapid formation of giant planets in our solar system and elsewhere (Boss 2007). Unfortunately, the initial structures of the protoplanets formed via gravitational instability are still unknown and different numerical models can be found to report different configurations (Helled and Schubert 2008; Helled and Bodenheimer 2011; Paul et al. 2012a, 2013). It is to be noted at this juncture that the planetary formation is highly dependent on the initial structures of the protoplanets. However, after the formation of the protoplanets some mechanisms are needed to form planets from them. As in Boss (1998b), dust grains present in these protoplanets would settle down under the action of gravity to form a solid core within the initial contraction time which lasts about 105 years. In their investigation, Helled et al. (2005) also found that during the initial contraction time, a silicate grain having initial size larger than about 0.01 cm can sediment to the core. Boss (1998b, 2004) demonstrated that dust growth and sedimentation may realistically occur inside gaseous protoplanets formed by disk instability. It is worth mentioning that McCrea and Williams (1965) were the first investigators of segregation problem who suggested that nonvolatile grains would settle to the centre of such protoplanets and so form a refractory core. The process was also investigated in more detail by Williams and Crampin (1971), Williams and Handbury (1974), Boss (1997), Helled et al. (2008), Paul et al. (2012a). However, in all the investigations, it is concluded that a core of terrestrial like material forms inside each of the protoplanets formed by disk instability in a reasonable short period of time in astronomical time scale. In calculating the sediment time, for simplicity, both McCrea and Williams (1965) and Williams and Crampin (1971) assumed a uniform density model of a protoplanet. This is a considerable assumption as virtually every known astronomical object is centrally condensed, this being necessary in order to have hydrostatic support. In their calculation, Boss (1998b) assumed the protoplanet to be in radiative equilibrium while Helled and Schubert (2008) found the gas blob to be fully convective with a thin outer radiative zone. This is consistent with Bodenheimer et al. (1980) and Wuchterl et al. (2000). On the other hand, Paul et al. (2012a, b) neglected the thin outer radiative zone and assumed the protoplanets to be fully convective, which is supported by Helled et al. (2005). In the recent past, Paul et al. (2008) has proposed conductive-radiative heat transport in investigating the initial structure of a protoplanet and concluded that the results obtained in the case of conductive-radiative heat transport are comparable with those attained in other investigations conducted with different heat transfers. Keeping the idea in mind, Paul et al. (2013) investigated the radius spectrum of solid grains inside gas giant protoplanets considering two models of heat transfer, namely convective and conductive-radiative and the results attained in both cases were found to be comparable and were found to be in a reasonable agreement with those obtained in some previous studies. But to the best of authors’ knowledge, the estimation of settling time is not investigated considering the conductive-radiative energy transport. Thus, the present study is an extension on that of Paul et al. (2013) in the case of conductive-radiative heat transfer.

The rest of the paper is organized as follows. “The problem statement” deals with the model equation with essential boundary conditions. The solution process is detailed in “Numerical estimate”. The obtained results and their discussion are presented in “Results and discussion”. Finally, Summary, and conclusions based on the obtained results are presented in “Summary and conclusion”.

The problem statement

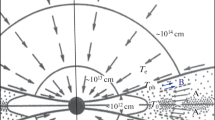
We start with an isolated spherical globe of gas with initial mass and radius comparable to one Jupiter mass i.e., M = 2 × 1030gm and R = 3 × 1012cm, respectively (see Paul et al. 2011). The globe is, in reality, a protoplanet and is taken to be isolated so that no external influences on it are included. The protoplanet is assumed to be of solar composition in quasi-static equilibrium with no core in which the ideal gas law holds well. Regarding the transfer of heat in the protoplanet, we have considered the conductive-radiative case proposed by Paul et al. (2008). The structure of the protoplanet in the assumed state is then given by the following set of equations:

The equation of hydrostatic equilibrium,

$$ \frac{dP(r)}{dr}=-\frac{GM(r)}{r^2}\rho (r). $$
(1)

The equation of conservation of mass,

$$ \frac{dM(r)}{dr}=4\pi {r}^2\rho (r). $$
(2)

The equation of conductive-radiative heat flux (see Paul et al. 2008),

$$ \left(\frac{8\sigma H}{3\times {10}^{-24}}\frac{T^3(r)}{\rho (r)}+\kappa \right)\frac{dT(r)}{dr}=-\frac{C}{4\pi R}\frac{GM^2(r)}{r^3}. $$
(3)

The Clausius-Clapeyron equation of state,

$$ P=\frac{k}{\mu H}\rho T. $$
(4)

The necessary boundary conditions are:

T(r) = 0, P(r) = 0 at r = R (surface),

M(r) = M at r = R,

M(r) = 0 at r = 0 (centre).

In Eqs. (1)–(3), κ is the thermal conductivity of the gas of the protoplanet and C = νμ. Here ν is a constant of order unity whose value depends on the internal structure of the system and the remaining symbols have been assumed to have their conventional meanings.

It is assumed that the composition of the gas of the protoplanet is solar, so the protoplanet will consist mainly of hydrogen and helium, but with a proportion λ by weight of heavy elements, mostly in the form of small grains. Following Helled and Schubert (2008), we have assumed silicate grains and allowed them to grow and settle down, as the grains composed of organic material will mostly be evaporated before they get to the core region, while water ice grains will completely be evaporated (Helled and Bodenheimer 2011). Let a grain, assumed to be spherical and solid, start moving from rest at the surface towards the centre of the protoplanet under the action of the gravitational field through the ambient gas. The gas offers resistance to the motion of the grain. Then the equation of motion of the grain at depth x below the surface is given by

$$ \frac{d}{dt}\left({m}_g\frac{dx}{dt}\right)=\frac{GM(x){m}_g}{{\left(R-x\right)}^2}-{F}_{res}, $$
(5)

where mg is the mass of the grain, G the universal gravitational constant, R the radius of the protoplanet, Fres the resistive force and M(x) is the mass interior to a radius R − x.

Since the temperature inside a protoplanet is fairly low, as we will see later, so the environment is quite favorable for the moving grain to coagulate between it and other grains that collide with it and grow. It is assumed that the travel speed of the grain is greater than the mean thermal speed of the grains. Then the equation giving the rate of growth of the grain is given by (see Baines and Williams 1965),

$$ \frac{dr_g}{dt}=\frac{\lambda \rho}{4{\rho}_g}\frac{dx}{dt} $$
(6)

where rg is the radius of the grain and ρg is the density of the grain material.

Solving Eq. (6), it is easy to see

$$ {r}_g={r}_0+\frac{\lambda }{4{\rho}_g}\underset{0.01}{\overset{x}{\int }}\rho dx. $$
(7)

Since the grain is growing, the correct form of resistance will be that due to Stokes’s, which leads to

$$ {F}_{res}=6\pi \eta\;{r}_g\frac{dx}{dt}, $$
(8)

where η is the coefficient of viscosity.

Numerical estimate

It is obvious that an analytic solution of Eq. (5), as it stands, is not possible. In general, any object moving in a resisting medium reaches a velocity close to its terminal velocity very quickly and then proceeds to travel at such a velocity (Williams and Cramprin 1971). We shall assume that this is the case for the falling grain under discussion and with this simplification Eq. (5) with the help of Eq. (8) can be put in the following form:

$$ 6\pi \eta {r}_g\frac{dx}{dt}=\frac{GM(x){m}_g}{{\left(R-x\right)}^2}. $$
(9)

Substitute \( {m}_g=\frac{4}{3}\pi {r}_g^3{\rho}_g \) and \( \eta ={\sigma}_k\sqrt{T} \)gm m−1 s−1 (see Podolak et al. 1988) in Eq. (9) to see

$$ \frac{dx}{dt}=\frac{2 GM(x){r}_g^2{\rho}_g}{9{\sigma}_k{\left(R-x\right)}^2\sqrt{T}}, $$
(10)

where σk = 8.6 × 10−6.

Let us replace the physical variables x, t, M(x), T(x), P(x) and rg by the non-dimensional variables y, τ, q, θ, p and Rg, respectively, with the help of the following transformations:

x = Ry, t = 107τ, M(x) = Mq, \( T(x)=\frac{\mu HGM}{kR}\theta \), \( P(x)=\frac{GM^2}{4\pi {R}^4}p \) and rg = r0Rg, where Rg is the non-dimensional radius of the grain and is given by

$$ {R}_g=1+\frac{\lambda M}{16{\pi \rho}_g{r}_0{R}^2}\underset{0.01}{\overset{y}{\int }}\frac{p}{\theta } dy $$
(11)

as in non-dimensional form, \( \rho =\frac{M}{4\pi {R}^3}\frac{p}{\theta } \).

Then Eq. (10) becomes

$$ \frac{d y}{d\tau}=\alpha \frac{qR_g^2}{{\left(1-y\right)}^2\sqrt{\theta }}, $$
(12)

where \( \alpha =\frac{2\times {10}^7{GMr}_0^2{\rho}_g\sqrt{kR}}{9{\sigma}_k{R}^3\sqrt{\mu HGM}} \).

Thus, the settling time of the falling grain is given by

$$ \tau =\underset{0.01}{\overset{0.99}{\int }}G\left(y,q,\theta, {R}_g\right)\; dy, $$
(13)

where

$$ G\left(y,q,\theta, {R}_g\right)=\frac{1}{\alpha}\frac{{\left(1-y\right)}^2\sqrt{\theta }}{qR_g^2}. $$
(14)

Whereas, the equations defining the structure of the protoplanet can be converted into a system of ordinary differential equations which on non-dimensionalisation with \( P(r)=\frac{GM^2}{4\pi {R}^4}p \), \( T(r)=\frac{\mu HGM}{kR}\theta \), M(r) = Mq, r = zR and then using z = 1 − y reduce to

$$ \frac{dp}{dy}=\frac{pq}{\theta {\left(1-y\right)}^2}, $$
(15)
$$ \frac{dq}{dy}=-\frac{p{\left(1-y\right)}^2}{\theta }, $$
(16)

and

$$ \frac{d\theta}{d y}=C\frac{\gamma {pq}^2}{{\left(1-y\right)}^3\left(\alpha {t}^4+\beta p\right)}\ \left(\mathrm{conductive}\hbox{-} \mathrm{radiative}\right), $$
(17)

where \( \alpha =\frac{8\sigma H}{3\times {10}^{-24}}{\left(\frac{\mu H GM}{kR}\right)}^3 \), \( \beta =\frac{M\kappa}{4\pi {R}^3} \) and \( \gamma =\frac{M^2k}{16{\pi}^2{R}^5\mu H} \).

The boundary conditions being

θ = 0, p = 0 at y = 0 (surface),

q = 1 at y = 0,

q = 0 at y = 1 (centre).

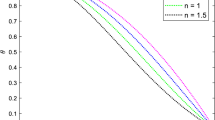
It is obvious that the integral in Eq. (13) cannot be evaluated analytically, so numerical techniques must have to be taken into account. Again, because of the existence of singularities in the model equations determining structure of the protoplanet, the integration cannot be started right from the surface. However, avoiding the surface or central singularities, the integration can easily be evaluated. To evaluate the integral in Eq. (13) numerically, we need the values of G(y, q, θ, R) at each spatial step. But G(y, q, θ, R) depends on y, q, θ and Rg. Also, Rg depends on p and θ. So, we need to know the values of p, q, θ and Rg for varying y. For the values of p, q and θ with varying y, we have solved Eqs. (15)–(17) by the classical Runge-Kutta method of order four. The value of the free parameter C has been used as 3.65 × 10−4 (see Paul et al. 2008). A detailed calculation for the values of p, q and θ for different values of y are available in Paul et al. (2008). For numerical calculations, we have used λ = 10−2 (Williams and Crampin 1971), ρg = 2.8 gm cm −3 (Paul et al. 2012a) and all other quantities involved in the problem have been assumed to have their standard values with the values of p and θ at different y, we have calculated Rg by the Trapezoidal rule of integration at these y’s for different grains with initial radii (5 × 10−3- 10−1cm). Inserting all the parameters involved together with these values of G and with the same step length, we have calculated the falling time by the Trapezoidal rule of numerical integration for all grain sizes considered. The obtained results are displayed in Figs. 1-2.

Fig. 1
figure 1

Distribution of non-dimensional physical variables p, q and θ

Full size image
Fig. 2
figure 2

Radius spectrum and settling times of grains having different initial radii, (a) distribution of grain radii rg; (b) cumulative settling time

Full size image

Results and discussion

In this study, we have investigated settling times of silicate grains having different initial radii on the basis of our estimated initial configuration of physical variables inside a Jovian like protoplanet formed via gravitational instability. Figure 1 depicts the configurations of non-dimensional physical variables (p, q and θ) obtained by solving Eqs. (15)–(17) with the approximated non-dimensionalized boundary conditions mentioned above. The obtained profiles for pressure, mass and temperature show a reasonable agreement with the results presented in the study due to Paul et al. (2012a, b, 2013), which were conducted considering the gas blob of the protoplanet to be fully convective. It is mentioned earlier that for grain sedimentation inside a protoplanet, the temperature should fairly be low. Our computed central temperature was found to be 946οK, which gets the guaranty of silicate grains sedimentation in our models as it is lower than the evaporation temperature of silicate grains. It is seen that the lower bound of the evaporation temperature of silicate grains is 1300οK(Helled and Schubert 2008; Nayakshin 2010).

Figures 2(a) and 2(b) picture the grain radius spectrum and cumulative settling time for the grains having initial radii 5 × 10−3−10−1cm, respectively. It is found from Fig. 2 that the grains with different initial radii grow more quickly after an initial brief period of time and settle down in the core region of the protoplanet in a reasonable short period of time in astronomical time scale. The radius spectrum (see Fig. 2a) of a Jupiter like protoplanet as obtained in our investigation strongly supports the results obtained in Paul et al. (2012b, 2013). It is also clear from the figure (Fig. 2a) that the grains of smaller initial radii settle down to the core region of the protoplanet acquiring almost the same radius as that attained by the grains having larger initial radii. The reason beneath may be that the grains with smaller initial radii grow even more quickly in the core region of the protoplanet because of higher number density of grains which leads to frequent collisions that result in further growth by the hit-and-stick mechanism (Paul et al. 2012a, b, 2013). Figure 2(b) depicts the settling times of the grains having different initial radii. It is perceived from the figure (Fig. 2b) that the grains with smaller initial radii take longer time to settle down which may be the result of the action of gravitational field and the ambient gas resistance unto the grain and grain sedimentation velocity. The sedimentation velocity of a grain depends on its size, grains having different size move with different speeds (Boss 1998a). Hence larger grains will settle faster than that of smaller ones (Nayakshin 2010). Also, small grains are strongly bound to the gas and hence the relative gas-grain velocity is small. Further, the grains with smaller initial radii face relatively lower resistance of ambient gas nearer to the surface of the protoplanet relative to the bigger ones. However, our computed results for settling time are found to be ~103 to ~105 yrs. that can be considered to be a satisfactory result with those attained in Boss (1998b), Helled and Schubert (2008), Helled et al. (2008), Nayakshin (2010), Paul et al. (2011, 2012a, b). In our study, the grains having initial radii of 5 × 10−3- 10−1cm are only allowed to grow. But realistically, grains having different sizes may be available in the protoplanets formed via disk instability. Observations of protoplanetary disks show evidence for (sub) micron and millimeter-sized or larger grains (see Weidenschilling 1984; Birnstiel et al. 2010). It is to be noted here that grains having radii smaller than the considered ones grow even more quickly to come into the considered size range (not displayed) (Paul et al. 2013). Grains with initial radii larger than the considered ones are not considered, because they are unrealistically large for initially formed protoplanets via disk instability (Boss 1997).

For a better perspective, we have presented our calculated settling time with those obtained in other studies, namely Paul et al. (2011) and Paul et al. (2012b) in Table 1. It is to be mentioned here that the study due to Paul et al. (2011) was conducted assuming the protoplanet to behave as a polytrope, whereas Paul et al. (2012b) investigated the grain sedimentation problem by considering the gas blob of the protoplanet to be in convective equilibrium. It is found from the table that our computed settling time is a little bit higher for every initial radius compared to the settling time obtained in Paul et al. (2011, 2012b) but it is consistent with those suggested by Boss (1998b), Helled et al. (2005). Therefore, it is suggestive that the heat transfer through the conductive-radiative process in a protoplanet can be a reality.

Table 1 Comparison of grain settling time in a Jupiter like protoplanet with different initial radii
Full size table

In this paper, we have used a constant value of the grains to gas ratio (λ) in the absence of any empirical formulae for it. Actually, the value of λ is not constant rather it is changed upon grain sedimentation. But we have tested its possible variation on grain growth and sedimentation and found to be insensitive. The results are also estimated for different endpoints with possible variations and the results, in this case, are generally found to support the presented ones. However, based on our computed results obtained in this communication, it can be pointed out here that grains with refectory materials can grow via hit-and-stick mechanism (cold welding process) and can settle down to the central region of a Jupiter like protoplanet in a reasonable short period of time in astronomical time scale.

Summary and conclusion

We have investigated settling times for falling grains inside a protoplanet. In our calculations, we have not assumed any density model for solving the problem. We have, rather, calculated the distribution of physical variables inside the protoplanet assuming the conductive-radiative heat transport proposed by Paul et al. (2008) and with this distribution, we have calculated the growth profiles of the grains having different initial radii (5 × 10−3-10−1 cm) and hence calculated the settling times required by the grains falling under the gravity of the protoplanet. The results are found to be in good agreement with those of Williams and Crampin (1971), Boss (1998b), Helled et al. (2008), and Paul et al. (2011, 2012a, b). We, therefore, conclude that a solid core composed almost entirely of refractory materials can be formed in the centre of a protoplanet due to the sedimentation of silicate grains by cold welding mechanism in a reasonable short period of time in astronomical time scale. Removal of gaseous envelopes from such protoplanets might produce terrestrial type planets.