On the optimality and practicability of mutual information analysis in some scenarios

Abstract

The best possible side-channel attack maximizes the success rate and would correspond to a maximum likelihood (ML) distinguisher if the leakage probabilities were totally known or accurately estimated in a profiling phase. When profiling is unavailable, however, it is not clear whether Mutual Information Analysis (MIA), Correlation Power Analysis (CPA), or Linear Regression Analysis (LRA) would be the most successful in a given scenario. In this paper, we show that MIA coincides with the maximum likelihood expression when leakage probabilities are replaced by online estimated probabilities. Moreover, we show that the calculation of MIA is lighter that the computation of the maximum likelihood. We then exhibit two case-studies where MIA outperforms CPA. One case is when the leakage model is known but the noise is not Gaussian. The second case is when the leakage model is partially unknown and the noise is Gaussian. In the latter scenario MIA is more efficient than LRA of any order.

1 Introduction

Many embedded systems implement cryptographic algorithms, which use secret keys that must be protected against extraction. Side-channel analysis (SCA) is one effective threat: physical quantities, such as instant power or radiated electromagnetic field, leak outside the embedded system boundary and reveal information about internal data. SCA consists in exploiting the link between the leakage signal and key-dependent internal data called sensitive variables.

The cryptographic algorithm is generally public information, whereas the implementation details are kept secret. For high-end security products, the confidentiality of the design is mandated by certification schemes, such as the Common Criteria [5]. For instance, to comply with ALC_DVS (Life-Cycle support – Development Security) requirement, the developer must provide a documentation that describes “all the physical, procedural, personnel, and other security measures that are necessary to protect the confidentiality and integrity of the TOE (target of evaluation) design and implementation in its development environment” [5, clause 2.1 C at page 141]. In particular, an attacker does not have enough information to precisely model the leakage of the device. On commercial products certified at highest evaluation assurance levels (EAL4+ or EAL5+), the attacker cannot set specific secret key values hence cannot profile the leakage.¹ Therefore, many side-channel attacks can only be performed online using some distinguisher.

Correlation Power Analysis (CPA) [1] is one common side-channel distinguisher. It is known [10, Theorem 5] that its optimality holds only for a specific noise model (Gaussian) and for a specific knowledge of the deterministic part of the leakage—namely it should be perfectly known up to an unknown scaling factor and an unknown offset.

Linear Regression Analysis (LRA) [6] has been proposed in the context where the leakage model is drifting apart from a Hamming weight model. Its parametric structure and ability to include several basis functions makes it a very powerful tool, that can adjust to a broad range of leakage models when the additive noise is Gaussian. Incidentally, CPA may be seen as a 2-dimensional LRA [10].

When both model and noise are partially or fully unknown, generic distinguishers have been proposed, such as Mutual Information Analysis (MIA) [8], Kolmogorov-Smirnov test [20, 23] or Cramér-von-Mises test [20, Section 3.3.]. Thorough investigations have been carried out (e.g., [2, 13, 21]) to identify strengths and weaknesses of various distinguishers in various scenarios, including empirical comparisons. In keeping with these results, we aim at showing some mathematical justification regarding MIA versus CPA and LRA. Our goal is thus to structure the field of attacks, by providing theoretical motivations why attacks strength may differ, irrespective of the particular trace datasets.

Contributions

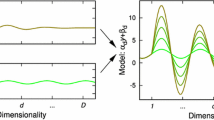
In this article, we derive MIA anew as the distinguisher which maximizes the success rate when the exact probabilities are replaced by online estimations. In order to assess the practicability of this mathematical result, we show two scenarios where MIA can outperform its competitors CPA and LRA, which themselves do not estimate probabilities. In these scenarios, we challenge the two hypotheses needed for CPA to be optimal: additive Gaussian noise and perfect knowledge of the model up to an affine transformation. This is illustrated in Fig. 1.

Fig. 1

Illustration of two practical situations where MIA can defeat CPA

Last, we extend the fast computation trick presented in [11] to MIA: the distinguisher is only computed from time to time based on histograms obtained by accumulation, where the accumulated histograms are shared for all the key guesses.

Organization

The remainder of this paper is organized as follows. Section 2 provides notations, assumptions, and the rigorous mathematical derivation that MIA reduces to a ML distinguisher, where exact leakage probabilities are replaced by online probabilities. Section 3 studies two examples where the attacker knows the one-bit model under non-Gaussian algorithmic noise, and for which MIA is shown to outperform CPA. Section 4 provides a scenario in which the leakage model is partially unknown under additive Gaussian noise, and where MIA outperforms CPA and LRA. Last, in Section 5, we propose a fast MIA computation deduced from our mathematical rewriting allowing to factor several computations. Section 6 concludes.

2 Optimality of mutual information analysis

2.1 Notations and assumptions

We assume that the attacker has at his disposal $\tilde {q}$ independent online leakage measurements² $\tilde {\mathbf {x}}=(\tilde {x}_{1},\ldots ,\tilde {x}_{\tilde {q}})$ ³ for some sequence of independent and uniformly distributed n-bit text words $\tilde {\mathbf {t}}=(\tilde {t}_{1},\ldots ,\tilde {t}_{\tilde {q}})$ (random but known). The n-bit secret key k ^∗ is fixed but unknown.

We do not make any precise assumption on the leakage model— in particular the attacker is not able to estimate the actual probability density in a profiling phase. Instead we choose an algorithmic-specific function f and a device-specific function φ to compute, for each key hypothesis k, sensitive values $\tilde {\mathbf {y}}=(\tilde {y}_{1},\ldots ,\tilde {y}_{\tilde {q}})$ by the formula

$$\begin{array}{@{}rcl@{}} \tilde{\mathbf{y}}=\varphi(f(k,\tilde{\mathbf{t}})), \end{array} $$

(1)

that is, $\tilde {y}_{i} = \varphi (f(k,\tilde {t}_{i}))$ for all $i=1,\ldots ,\tilde {q}$. In practice, a suitable choice of φ should be optimized depending on some leakage model but in what follows, f and φ can be taken arbitrarily such that they fulfill the following Markov condition.

Assumption 1 (Markov condition)

The leakage $\tilde {\mathbf {x}}$ depends on the actual secret key k ^∗ only through the computed model $\tilde {\mathbf {y}}=\varphi (f(k^{*},\tilde {\mathbf {t}}))$ .

Thus, while the conditional distribution $\mathbb {P}_{k}(\tilde {\mathbf {x}}|\tilde {\mathbf {t}})$ depends on the value k of the secret key, the expression $\mathbb {P}(\tilde {\mathbf {x}}|\tilde {\mathbf {y}})$ depends on k only through $\tilde {\mathbf {y}}=\varphi (f(k,\tilde {\mathbf {t}}))$. If we let $\mathbb {P}_{k}(\tilde {\mathbf {x}},\tilde {\mathbf {t}})$ be the joint probability distribution of $\tilde {\mathbf {x}}$ and $\tilde {\mathbf {t}}$ when k ^∗ = k, one has the Fisher factorization [3]

$$\begin{array}{@{}rcl@{}} \mathbb{P}_{k}(\tilde{\mathbf{x}},\tilde{\mathbf{t}}) = \mathbb{P}(\tilde{\mathbf{t}}) \mathbb{P}_{k}(\tilde{\mathbf{x}}|\tilde{\mathbf{t}}) = \mathbb{P}(\tilde{\mathbf{t}}) \mathbb{P}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}) \qquad \text{ where }\tilde{\mathbf{y}}=\varphi(f(k,\tilde{\mathbf{t}})). \end{array} $$

(2)

In the latter expression we have $\mathbb {P}(\tilde {\mathbf {t}})\,=\,2^{-\tilde {q} n}$ since all text n-bit words are assumed independent and identically uniformly distributed.

In the case of an additive noise model, we simply have $\tilde {\mathbf {x}}=\tilde {\mathbf {y}}+\tilde {\mathbf {n}}$ where $\tilde {\mathbf {n}}$ is the noise vector, and the Markov condition is obviously satisfied. In general, in order to fulfill the Markov condition the attacker needs some knowledge on the actual leakage model. We give two examples regarding the Markov condition:

Example 1

If leakage x _i is linked to t _i and k ^∗ through the relationship x _i = w _H (k ^∗⊕ t _i ) + n _i for all $i=1,\ldots ,\tilde {q}$, where w _H is the Hamming weight and n _i is the noise (independent of t _i ), then both models y _i = k ⊕ t _i and y _i = w _H (k ⊕ t _i ) satisfy the Markov condition.⁴ Sections 3 and 4 give other, more sophisticated, examples that satisfy the Markov condition.

Example 2

In the same scenario as in Example 1, consider the bit-dropping strategy (called 7LSB in [8] and used in [18, 22]). Then e.g., y _i = (k ⊕ t _i )[1 : 7] (the first seven bit components) does not satisfy the Markov condition. Note that the leakage model in this example intentionally discards some information, hence may not be satisfactory [18].

Let $\tilde {k}$ be the key estimate that maximizes a distinguisher $\mathcal {D}$ given $\tilde {\mathbf {x}}$ and $\tilde {\mathbf {t}}$, i.e.,

$$ \tilde k = \arg\max\limits_{k\in \mathcal K} \ \mathcal{D} (\tilde{\mathbf{x}},\tilde{\mathbf{y}}) $$

(5)

where $\mathcal {K}$ is the key space.

We also assume that leakage values are quantized⁵ in a suitable finite set $\mathcal {X}$. Letting $\mathcal {Y}$ denote the discrete sensitive value space, we have $\tilde {\mathbf {x}}\in {\mathcal X}^{\tilde {q}}$ and $\tilde {\mathbf {y}}\in {\mathcal Y}^{\tilde {q}}$. The actual probability densities being unknown, the attacker estimates them online, during the attack, from the available data in the sequences $\tilde {\mathbf {x}}$ and $\tilde {\mathbf {y}}$ (via $\tilde {\mathbf {t}}$), by counting all instances of possible values of $x\in \mathcal {X}$ and $y\in \mathcal {Y}$:

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(x) &=& \frac{1}{\tilde{q}}\sum\limits_{i=1}^{\tilde{q}} \; \mathbb{1}_{\tilde{x}_{i}=x}, \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(y) &=& \frac{1}{\tilde{q}}\sum\limits_{i=1}^{\tilde{q}} \; \mathbb{1}_{\tilde{y}_{i}=y}, \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(x,y) &=& \frac{1}{\tilde{q}}\sum\limits_{i=1}^{\tilde{q}} \; \mathbb{1}_{\tilde{x}_{i}=x, \tilde{y}_{i}=y}, \end{array} $$

(8)

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(x|y) &=& \frac{{\sum}_{i=1}^{\tilde{q}} \mathbb{1}_{\tilde{x}_{i}=x, \tilde{y}_{i}=y} }{ {\sum}_{i=1}^{\tilde{q}} \; \mathbb{1}_{\tilde{y}_{i}=\tilde{y}}} = \frac{\tilde{\mathbb{P}}(x,y)}{\tilde{\mathbb{P}}(y)}, \end{array} $$

(9)

where $\mathbb {1}_{A}$ denotes the indicator function of A: $\mathbb {1}_{A}=1$ if A is true and = 0 otherwise.

Definition 1 (Empirical Mutual Information)

The empirical mutual information is defined as

$$\begin{array}{@{}rcl@{}} \tilde{I}(\tilde{\mathbf{x}},\tilde{\mathbf{y}}) = \sum\limits_{x\in\mathcal{X},y\in\mathcal{Y}} \tilde{\mathbb{P}}(x,y) \ \log_{2} \frac{\tilde{\mathbb{P}}(x,y) }{ \tilde{\mathbb{P}}(x) \tilde{\mathbb{P}}(y)}, \end{array} $$

(10)

which can also be written as

$$\begin{array}{@{}rcl@{}} \tilde{I}(\tilde{\mathbf{x}},\tilde{\mathbf{y}}) = \tilde{H}(\tilde{\mathbf{x}}) - \tilde{H}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}) , \end{array} $$

(11)

where the empirical entropies are defined as

$$\begin{array}{@{}rcl@{}} \tilde{H}(\tilde{\mathbf{x}}) = \sum\limits_{x\in\mathcal{X}} \ \tilde{\mathbb{P}}(x) \ \log_{2} \frac{1}{ \tilde{\mathbb{P}}(x) } \end{array} $$

(12)

and

$$\begin{array}{@{}rcl@{}} \tilde{H}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}) =\sum\limits_{x\in\mathcal{X},y\in\mathcal{Y}} \tilde{\mathbb{P}}(x,y) \ \log_{2} \frac{1}{\tilde{\mathbb{P}}(x|y)}. \end{array} $$

(13)

These quantities are functions of the sequences $\tilde {\mathbf {x}}$ and $\tilde {\mathbf {y}}$ since $\tilde {\mathbb {P}}(x,y)$ is a function of $\tilde {\mathbf {x}}$ and $\tilde {\mathbf {y}}$. They also depend on the key guessed value k, via the expression of $\tilde {\mathbf {y}}$.

2.2 Mathematical derivation

In this subsection, we show that MIA coincides with the ML expression where leakage probabilities $\mathbb {P}$ are replaced by online estimated probabilities $\tilde {\mathbb {P}}$.

Definition 2

(Success Rate [19, Sec. 3.1]) The success rate (averaged over all possible secret key values) is defined as

$$\begin{array}{@{}rcl@{}} {\text{SR}}=\frac{1}{2^{n}}\sum\limits_{k=0}^{2^{n}-1} \mathbb{P}_{k}(\tilde{k}=k) . \end{array} $$

(14)

Here we follow a frequentist approach. An equivalent alternative Bayesian approach would be to assume a uniform prior key distribution [10].

Theorem 3 (Maximum Likelihood 4)

Let $\tilde {\mathbf {y}}=\varphi (f(k,\tilde {\mathbf {t}}))$ . The optimal key estimate that maximizes the success rate (14) is

$$\begin{array}{@{}rcl@{}} \tilde{k} = \arg\max\limits_{k} \, \mathbb{P}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}). \end{array} $$

(15)

Proof

We give here a formal proof, which nicely relates to Definition 2. Straightforward computation yields

$$\begin{array}{@{}rcl@{}} {\text{SR}} &=&\frac{1}{2^{n}}\sum\limits_{k=1}^{2^{n}} \sum\limits_{\tilde{\mathbf{x}},\tilde{\mathbf{t}}} \ \mathbb{P}_{k}(\tilde{\mathbf{x}},\tilde{\mathbf{t}}) \ \mathbb{1}_{k=\tilde{k}} \end{array} $$

(16)

$$\begin{array}{@{}rcl@{}} &=& \frac{1}{2^{n}}\sum\limits_{k=1}^{2^{n}} \sum\limits_{\tilde{\mathbf{x}},\tilde{\mathbf{t}}} \ \mathbb{P}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}=\varphi(f(k,\tilde{\mathbf{t}}))) \ \mathbb{P}(\tilde{\mathbf{t}}) \ \mathbb{1}_{k=\tilde{k}} \quad\text{(by~(2) \& Assumption~1)} \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} &=& \frac{1}{2^{n(\tilde{q}+1)}}\sum\limits_{k=1}^{2^{n}} \sum\limits_{\tilde{\mathbf{x}},\tilde{\mathbf{t}}} \ \mathbb{P}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}=\varphi(f(k,\tilde{\mathbf{t}}))) \ \mathbb{1}_{k=\tilde{k}} \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} &=& \frac{1}{2^{n(\tilde{q}+1)}} \sum\limits_{\tilde{\mathbf{x}},\tilde{\mathbf{t}}} \ \mathbb{P}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}=\varphi(f(k=\tilde{k},\tilde{\mathbf{t}}))). \end{array} $$

(19)

Thus, for each given sequences $\tilde {\mathbf {x}},\tilde {\mathbf {t}}$ maximizing the success rate amounts to choosing $k=\tilde {k}$ so as to maximize $\mathbb {P}(\tilde {\mathbf {x}}|\tilde {\mathbf {y}}) = \mathbb {P}(\tilde {\mathbf {x}}|\tilde {\mathbf {y}}=\varphi (f(k=\tilde {k},\tilde {\mathbf {t}})))$:

$$\begin{array}{@{}rcl@{}} \tilde{k} = \arg\max\limits_{k} \, \mathbb{P}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}) . \end{array} $$

(20)

□

When no profiling is possible the conditional distribution

$$\begin{array}{@{}rcl@{}} \mathbb{P}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}})=\prod\limits_{i=1}^{\tilde{q}} \, \mathbb{P}(\tilde{x}_{i}|\tilde{y}_{i}) \end{array} $$

(21)

is unknown to the attacker. Therefore, Theorem 3 is no longer practical and we require a universal ⁶ version of it.

Definition 3 (Universal Maximum Likelihood)

Let $\tilde {\mathbf {y}}=\varphi (f(k,\tilde {\mathbf {t}}))$. The universal maximum likelihood (UML) key estimate is defined by

$$\begin{array}{@{}rcl@{}} \tilde{k} = \arg\max\limits_{k} \, \tilde{\mathbb{P}}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}) , \end{array} $$

(22)

where

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}})=\prod\limits_{i=1}^{\tilde{q}} \, \tilde{\mathbb{P}}(\tilde{x}_{i}|\tilde{y}_{i}). \end{array} $$

(23)

Here $\tilde {\mathbb {P}}$, defined in (9), (8), (7) and (6), is estimated directly from the available data, that is, from the actual values in the sequences $\tilde {\mathbf {x}}$ and $\tilde {\mathbf {y}}$.

Theorem 4 (UML is MIA)

The universal maximum likelihood key estimate is equivalent to the mutual information analysis[8]:

$$\begin{array}{@{}rcl@{}} \tilde{k} = \arg\max\limits_{k} \, \tilde{\mathbb{P}}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}}) = \arg\max\limits_{k} \ \tilde{I}(\tilde{\mathbf{x}},\tilde{\mathbf{y}}) , \end{array} $$

(24)

where $\tilde {I}(\tilde {\mathbf {x}},\tilde {\mathbf {y}})$ is the universal mutual information (Definition 1).

Proof

Rearrange the likelihood product according to values taken by the $\tilde {x}_{i}$ and $\tilde {y}_{i}$’s:

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}})=\prod\limits_{i=1}^{\tilde{q}} \, \tilde{\mathbb{P}}(\tilde{x}_{i}|\tilde{y}_{i}) =\prod\limits_{x\in\mathcal{X},y\in\mathcal{Y}} \tilde{\mathbb{P}}(x|y)^{\tilde{n}_{x,y}} \end{array} $$

(25)

where $\tilde {n}_{x,y}$ is the number of components $(\tilde {x}_{i},\tilde {y}_{i})$ equal to (x,y), i.e.,

$$\begin{array}{@{}rcl@{}} \tilde{n}_{x,y}= \sum\limits_{i=1}^{\tilde{q}} \, \mathbb{1}_{\tilde{x}_{i}=x, \tilde{y}_{i}=y} = \tilde{q} \;\tilde{\mathbb{P}}(x,y) . \end{array} $$

(26)

The second equality in (25) is based on a counting argument: some events collide, i.e., we have $(x_{i},y_{i})=(x_{i^{\prime }},y_{i^{\prime }})$ for i≠i ^′. The exponent $\tilde {n}_{x,y}$ is meant to enumerate all such possible collisions. This gives

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}})= \prod\limits_{x\in\mathcal{X},y\in\mathcal{Y}} \tilde{\mathbb{P}}(x|y)^{\tilde{q} \;\tilde{\mathbb{P}}(x,y) } = 2^{-\tilde{q} \tilde{H}(\tilde{\mathbf{x}}|\tilde{\mathbf{y}})}, \end{array} $$

(27)

(see Definition 1). Therefore, maximizing $\tilde {\mathbb {P}}(\tilde {\mathbf {x}}| \tilde {\mathbf {y}})$ amounts to minimizing the empirical conditional entropy $\tilde {H}(\tilde {\mathbf {x}}| \tilde {\mathbf {y}})$. Since $\tilde {H}(\tilde {\mathbf {x}})$ is key-independent, this in turn amounts to maximizing the empirical mutual information $\tilde {I}(\tilde {\mathbf {x}},\tilde {\mathbf {y}})=\tilde {H}(\tilde {\mathbf {x}}) - \tilde {H}(\tilde {\mathbf {x}}|\tilde {\mathbf {y}})$. □

From Theorem 4 we can conclude that MIA is “optimal” as a universal maximum likelihood estimation. This constitutes a rigorous proof that mutual information is a relevant tool for key recovery when the leakage is unknown (in the case where the model satisfies the Markov condition) as was already hinted in [8, 16, 18, 21].

Corollary 5

MIA coincides with the ML distinguisher as $\tilde {q}\to \infty$ .

Proof

By the law of large numbers, the online probability $\tilde {\mathbb {P}}$ converges almost surely to the exact probability of the leakage as $\tilde {q}\to \infty$. For any fixed values of $\tilde {x}\in \mathcal {X}, \tilde {y}\in \mathcal {Y}$,

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(\tilde{x}|\tilde{y}) \ {\underset{\tilde{q}\to\infty}{\longrightarrow}} \ \mathbb{P}(\tilde{x}|\tilde{y}) \qquad a.s. \end{array} $$

Thus in the limit, MIA coincides with the ML rule. □

Remark 1

It is well known [16] that if the mapping $\tilde {t} \mapsto \tilde {y}=\varphi (f(k,\tilde {t}))$ is one-to-one (for all values of k), then MIA cannot distinguish the correct key. This is also clear from (4) in footnote 4: given two different keys k,k ^′, there is a bijection between y _k and $y_{k^{\prime }}$, which is simply $\beta = y_{k^{\prime }} \circ y_{k}^{-1}$. In our present setting this is easily seen by noting that when $\tilde {y}=\varphi (f(k,\tilde {t}))$,

$$\begin{array}{@{}rcl@{}} \tilde{\mathbb{P}}(x|y) = \frac{{\sum}_{i=1}^{\tilde{q}} \mathbb{1}_{\tilde{x}_{i}=x, \tilde{y}_{i}=y} }{ {\sum}_{i=1}^{\tilde{q}} \mathbb{1}_{\tilde{y}_{i}=y}}= \frac{{\sum}_{i=1}^{\tilde{q}} \mathbb{1}_{\tilde{x}_{i}=x, \tilde{t}_{i}=t} }{ {\sum}_{i=1}^{\tilde{q}} \mathbb{1}_{\tilde{t}_{i}=t}} \end{array} $$

(28)

is independent of the value k. Note that this is true for any fixed number of measurements $\tilde {q}$ during the attack.

2.3 MIA faster than ML distinguisher

Now that we have shown that the Universal ML distinguisher is strictly equivalent to the MIA distinguisher, we show that the use of the MIA Distinguisher is cheaper in terms of calculations than the ML distinguisher. Both distinguishers require the knowledge of $\tilde {\mathbb {P}}$, the online estimation of the leakage probability. However, the summation is not exactly the same:

• the ML distinguisher consists in a sum of $\tilde {q}$ logarithms, whereas

• the MIA involves a sum over $|\mathcal {X}|\times |\mathcal {Y}|$ logarithms.⁷

This means that computing a ML requires $\tilde {q}$ logarithm computations while computing a MIA requires $|\mathcal {X}|\times |\mathcal {Y}|$ logarithm computations. As long as $|\mathcal {X}|\times |\mathcal {Y}|$ is smaller than $\tilde {q}$, which is verified for practical signal-to-noise values, the MIA is faster than the ML in terms of logarithm computations. Furthermore, in Section 5.2, we present a fast algorithm to compute MIA; it takes advantage of precomputations, which are similar to that already presented in [11].

3 Non-gaussian noise challenge

In this section, we show two examples where MIA outperforms CPA due to non-Gaussian noise. The first example presented in Section 3.1 is an academic (albeit artificial) example built in order to have the success rate of CPA collapse. The second example in Section 3.2 is more practical.

3.1 Pedagogical case-study

We consider a setup where the variables are X = Y + N, with Y = φ(f(k ^∗,T)), where Y ∈{±1}, and $N\sim \mathcal {U}(\{\pm \sigma \})$ (meaning that N takes values − σ and + σ randomly, with probabilities $\frac 12$ and $\frac 12$), where σ is an integer. Specifically, we assume that k ^∗, $t{\in \mathbb F_{2}^{n}}$, with n = 4, and that $f: {\mathbb F_{2}^{n}}{\times \mathbb F_{2}^{n}}{\to \mathbb F_{2}^{m}}$ is a (truncated version) of the SERPENT Sbox⁸ fed by the XOR of the two inputs (key and plaintext nibbles) and φ = w _H is the Hamming weight (which reduces to the identity $\mathbb F_{2}\to \mathbb F_{2}$ if m = 1 bit).

The optimal distinguisher (Theorem 3) in this scenario has the following closed-form expression:

$$\begin{array}{@{}rcl@{}} \mathcal{D}(\tilde{\mathbf{x}}, \tilde{\mathbf{t}}) = \arg\max_{k} \;\mathbb{P} (\tilde{\mathbf{x}}|\tilde{\mathbf{t}}, k) = \arg\max_{k} \frac1{2^{\tilde{q}}} {\prod}_{i=1}^{\tilde{q}} \delta(\tilde{x}_{i}, \tilde{t}_{i}, k) , \end{array} $$

(29)

where $\delta : { \mathbb F_{2}^{m}} \times { \mathbb F_{2}^{n}} \times { \mathbb F_{2}^{n}} \to \{0,1\}$ is defined as

$$\begin{array}{@{}rcl@{}} \delta(x, t, k) = \left\{\begin{array}{ll} 1 & \text{ if } x - \varphi(f(k,t)) = -\sigma ,\\ 1 & \text{ if } x - \varphi(f(k,t)) = +\sigma ,\\ 0 & \text{ otherwise } .\\ \end{array}\right. \end{array} $$

The evaluation of this quantity requires the knowledge of σ, which by definition is an unknown quantity related to the noise. Our simulations have been carried out as follows.

• 1. Generate two large uniformly distributed random vectors $\tilde {\mathbf {t}}$ and $\tilde {\mathbf {n}}$ of length $\tilde {q}$;

• 2. Deliver the pair of vectors $(\tilde {\mathbf {t}},\tilde {\mathbf {x}}=\varphi (f(k^{*},\tilde {\mathbf {t}}))+\tilde {\mathbf {n}})$ to the attacker;

• 3. Estimate averages and PMFs (probability mass functions) of this data for $\tilde {q}_{\mathsf {step}}$ (= 1), then for $2 \tilde {q}_{\mathsf {step}}$, $3 \tilde {q}_{\mathsf {step}}$ and so on;

• 4. At each multiple of $\tilde {q}_{\mathsf {step}}$, carry out CPA and MIA.

The attacks are reproduced 100 times to allow for narrow error bars on the estimated success rate.

Remark 2

We do not consider linear regression analysis here because the model is not parametric. The only unknown parameter is related to the noisy part of the leakage, not its deterministic part.

Simulation results are given in Fig. 2 for σ = 2 and σ = 4. The success rate of the “optimal” distinguisher (the ML distinguisher of Theorem 3 – see (29)) is drawn in order to visualize the limit between feasible (below) and unfeasible (above) attacks. It can be seen that MIA is almost as successful as the ML distinguisher, despite the knowledge of the value of σ is not required for the MIA. In addition, one can see that the CPA performs worse, and all the worst as σ increases. In this case, the CPA is not the optimal distinguisher (as e.g., underlined in [10, Theorem 5]) since the noise is not Gaussian (but discrete).

Fig. 2

Success rate for σ = 2 (left) and σ = 4 (right), when $Y\sim \mathcal {U}(\{\pm 1\})$ and $N\sim \mathcal {U}(\{\pm \sigma \})$

Remark 3

Another attack strategy for the leakage model presented in this subsection would simply be to filter out the noise. One could for instance dispose of all traces where the leakage is negative. The remaining traces (half of them) contain a constant noise N = + σ > 1, hence the signal Y can be read out without noise. Such attack, known as the subset attack [14, Sec. 5.2], is not far from the optimal one (29). It actually does coincide with the optimal attack if the attacker recovers Y from both subsets {i/X _i > 0} and {i/X _i < 0}. Still, it can be noted that MIA is very close to being optimal for this scenario.

Asymptotics

We can estimate the theoretical quantities for CPA and MIA as follows. We have V a r(Y ) = 1 and V a r(N) = σ ², hence a signal to noise ratio SNR = 1/σ ². In addition, X can only take four values: ± 1 ± σ. Since $\mathbb {E}(XY) = \mathbb {E}(X^{2}) + \mathbb {E}(YN) = Var(X) + \mathbb {E}(Y) \mathbb {E}(N) = 1 + 0 \times 0 = 1$, the correlation is simply ρ(X,Y ) = 1/σ, which vanishes as σ increases.

However, for σ > 1, the mutual information I(X,Y ) = 1 bit. Indeed, $\mathsf {H}(X) = - {\sum }_{x\in \{\pm 1\pm \sigma \}} \mathbb {P}(X=x) \log _{2} \mathbb {P}(X=x) = - {\sum }_{x\in \{\pm 1\pm \sigma \}} \frac 14 \log _{2} \frac 14 = \log _{2} 4 = 2$ bits, H(X|y = ±1) = log 22 = 1 bit, so $\mathsf {I}(X,Y) = \log _{2} 4 - {\sum }_{y\in \{\pm 1\}} \mathbb {P}(X=x) \log _{2} 2 = \log _{2} 4 - \log _{2} 2 = 1$ bit, irrespective of $\sigma \in \mathbb {N}$.

The important fact is that the mutual information does not depend on the value of σ. Accordingly, it can be seen from Fig. 2 that the success rate of the MIA is not affected by the noise variance. This explains why MIA will outperform the CPA for large enough σ.

3.2 Application to bitslice PRESENT

Bitslicing algorithms is a common practice. This holds both for standard [17] (e.g., AES) and lightweight [12] (PRESENT, Piccolo) block ciphers. Here the distinguishers must be single-bit: Y ∈{±1}. However, compared to the case of Section 3.1, the noise takes now more than two values: On an 8-bit computer, the 7 other bits will leak independently. They are, however, not concerned by the attack, and constitute algorithmic noise N which follows a binomial law $\alpha \times \mathcal {B}(7,\frac 12)$, where α is a scaling factor.

Simulation results for various values of α are in Fig. 3. Interestingly, MIA is efficient for the cases where the leakage $Y\!\sim \!\mathcal {U}(\{\pm 1\})$ is not altered by the addition of noise: For α = 0.8 and α = 2.0, it is still possible to tell unambiguously from X what is the value of Y. On the contrary, when α = 0.5 or α = 1.0, the function (Y,N)↦X = Y + N is not one-to-one. For instance, in the case α = 1.0, the value X = 2 can result as well from Y = −1 and N = 3, or Y = +1 and N = 2 (see Fig. 4).

Fig. 3

Success rate for the attack of a bitsliced algorithm on an 8-bit processor, where 7 bits make up algorithmic noise, and have weight 0.5, 1.0 (top) and 0.8 and 2.0 (bottom)

Fig. 4

Illustration of bijectivity (left) vs. non-injectivity (right) of the leakage function

4 Partially unknown model challenge

Veyrat-Charvillon and Standaert [20, section 4] have already noticed that MIA can outperform CPA if the model is drifted too far away from the real leakage. However, LRA is able to make up for the model drift of [20] (which considered unevenly weighted bits). In this section, we challenge CPA and LRA with a partially unknown model. We show that, in our example, MIA has a much better success rate than both CPA and LRA.

For our empirical study we used the following setup:

$$X = \psi(Y(k^{*})) + N, \qquad Y(k^{*}) = w_{H}(\operatorname{Sbox}(k^{*} \oplus T)), $$

where Sbox is the AES substitution box, ψ is the non-linear function given by:

x	0	1	2	3	4	5	6	7	8
ψ(x)	+ 1	+ 2	+ 3	+ 4	0	− 4	− 3	− 2	− 1

which is unknown to the attacker, and N is a centered Gaussian noise with unknown standard deviation σ. The non-linearity of ψ is motivated by [13], where it is discussed that a linear model favors CPA over MIA.

The leakage is continuous due to the Gaussian noise. In order to discretize the leakage to obtain discrete probabilities, we used the binning method. We conducted MIA with several different binning sizes:

$$\begin{array}{@{}rcl@{}} B = \{ [(i-1) \times {\Delta} x, i \times {\Delta} x[,\, i\in\mathbb{Z} \} \qquad\text{for } {\Delta} x = \{ 1, 3, 5, 7, 9\} . \end{array} $$

(30)

In this paper, we do not try to establish any specific result about binning, but content ourselves to present empirical results obtained with different bin sizes.

We have carried out LRA for the standard basis in dimension d = 9 and higher dimensions d = {37,93,163}. More precisely, for d = 9 we have $\tilde {\mathbf {y}}^{\prime }(k) \,=\, (\vec 1,\tilde {\mathbf {y}}_{1}(k),\tilde {\mathbf {y}}_{2}(k),\ldots ,\tilde {\mathbf {y}}_{8}(k))$ with $\tilde {\mathbf {y}}_{j}(k) = [\operatorname {Sbox}(k \oplus T)]_{j}$ where $[\cdot ]_{j} : {\mathbb F^{n}_{2}} \to \mathbb F_{2}$ is the projection mapping onto the j-th bit and where $\vec {1}$ an all-one string. For d = 37 the attacker additionally takes into consideration the products between all possible $\tilde {\mathbf {y}}_{j}$ (1 ≤ j ≤ 8), i.e., $\tilde {\mathbf {y}}_{1} \cdot \tilde {\mathbf {y}}_{2}, \tilde {\mathbf {y}}_{1} \cdot \tilde {\mathbf {y}}_{3}, \tilde {\mathbf {y}}_{1} \cdot \tilde {\mathbf {y}}_{4}$ and so on. Consequently, d = 93 considers additionally the product between three $\tilde {\mathbf {y}}$’s and d = 163 includes also all possible product combinations with four columns. See [9] for a detailed description on the selection of basis functions.

Figure 5 shows the success rate using 100 independent experiments. Perhaps surprisingly, MIA turns out to be more efficient than LRA. Quite naturally, MIA and LRA become closer as the the variance of the independent measurement noise N increases. It can be seen that LRA using higher dimension requires a sufficient number of traces for estimation (for d = 37 around 100, d = 93 around 150, and d = 137 failed below 200 traces). Consequently, in this scenario using high dimensions is not appropriate, even if the high dimension in question might fit the unknown function ψ.

Fig. 5

Success rate for σ ∈{0,1,2,3} when the model is unknown

One reason why MIA outperforms CPA and LRA in this scenario is that the function ψ was chosen to have a null covariance. Moreover, one can observe that the most efficient binning size depends on the noise variance and thus on the scattering of the leakage. As σ increases, larger values of Δ should be chosen. This is contrary to the suggestions made in [8], which proposes to estimate the probability distributions as accurately as possible and thus to consider as many bins as there are distinct values in the traces. In our experiments, when noise is absent (σ = 0) the optimal binning size is Δ = 1 which is equivalent to the step size of Y, while for σ = 2 the optimal binning is Δ = 5 (see Fig. 5c).

It can be seen that using 40 traces the success rate of MIA with Δ = 5 reaches 90%, whereas using Δ = 1 it is only about 30%. To understand this phenomenon, Fig. 6 displays the estimated $\tilde {\mathbb {P}}(x|y)$ in a 3D histogram for the correct key and one false key hypothesis, such that MIA is able to reveal the correct key using Δ = 5 but fails for Δ = 1. Clearly, the distinguishability between the correct and false key is much higher in case of Δ = 5 than for Δ = 1.

Fig. 6

Estimated $\tilde {\mathbb {P}}(X|Y)$ using 40 traces for σ = 2 (see Fig. 5c)

More precisely, as the leakage is dispersed by the noise the population of bins of the false key becomes similar to the the ones of the correct key when considering smaller binning size (compare Fig. 6a and b). In contrast, the difference is more visible when the leakage is quantified into larger bins (compare Fig. 6c and d). Therefore, even if the estimation of $\tilde {I}(\tilde {\mathbf {x}},\tilde {\mathbf {y}})$ using $\tilde {\mathbb {P}}(x|y)$ for larger Δ is coarser and thus looses some information, the distinguishing ability to reveal the correct key is enhanced.

5 Fast computations

In this section, we explain how we compute CPA and MIA in a faster way. We first show an algorithm for CPA, then for MIA.

5.1 Fast computation of CPA

We recall here the definition of empirical CPA:

$$\begin{array}{@{}rcl@{}} \rho(X,Y(k)) &=& \frac{\frac1m {\sum}_{i=1}^{m} x_{i} y_{i}(k) - \left( \frac1m {\sum}_{i=1}^{m} x_{i} \right) \left( \frac1m {\sum}_{i=1}^{m} y_{i}(k) \right)}{ \sqrt{\frac1m {\sum}_{i=1}^{m} {x_{i}^{2}} - \left( \frac1m {\sum}_{i=1}^{m} x_{i} \right)^{2}} \sqrt{\frac1m {\sum}_{i=1}^{m} {y_{i}^{2}}(k) - \left( \frac1m {\sum}_{i=1}^{m} y_{i}(k) \right)^{2}}} \\ &=& \frac{m {\sum}_{i=1}^{m} x_{i} y_{i}(k) - \left( {\sum}_{i=1}^{m} x_{i} \right) \left( {\sum}_{i=1}^{m} y_{i}(k) \right)}{ \sqrt{m {\sum}_{i=1}^{m} {x_{i}^{2}} - \left( {\sum}_{i=1}^{m} x_{i} \right)^{2}} \sqrt{m {\sum}_{i=1}^{m} {y_{i}^{2}}(k) - \left( {\sum}_{i=1}^{m} y_{i}(k) \right)^{2}}} , \end{array} $$

(31)

where y _i (k) = φ(f(k,t _i )). For the fast computation the following accumulators are required:

• $\mathsf {sx}[t] = {\sum }_{i/t_{i}=t} x_{i}$, the sum of leakages for a common t;

• $\mathsf {sx}2[t] = {\sum }_{i/t_{i}=t} {x_{i}^{2}}$, the sum of leakage squares for a common t;

• $\mathsf {qt} [t] = {\sum }_{i/t_{i}=t} 1$, the number of t which occurred.

We detail the various terms in the next two paragraphs.

5.1.1 Averages

First, we simply have

$$\sum\limits_{i=1}^{m} x_{i} = \sum\limits_{t} \mathsf{sx}[t] , $$

which is key independent. Second,

$$\begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{m} y_{i} &=& \sum\limits_{t} \sum\limits_{i / t_{i}=t} y_{i} \\ &=& \sum\limits_{t} \sum\limits_{i / t_{i}=t} \varphi(f(k,t_{i})) \\ &=& \sum\limits_{t} \varphi(f(k,t_{i})) \mathsf{qt}[t] , \end{array} $$

which, quite surprisingly, is key independent.

5.1.2 Scalar product

The scalar product can be written the following way:

$$\begin{array}{@{}rcl@{}} {\sum}_{i=1}^{m} x_{i} y_{i} &=& {\sum}_{y} {\sum}_{i / y_{i}=y} x_{i} y_{i} \\ &=& {\sum}_{y} y {\sum}_{i / y_{i}=y} x_{i} \\ &=& {\sum}_{y} y {\sum}_{i / \varphi(f(k,t_{i}))=y} x_{i} \\ &=& {\sum}_{y} y \ \mathsf{sx}^{\prime}[y] , \end{array} $$

where $\mathsf {sx}^{\prime }[y] = {\sum }_{t / \varphi (f(k,t))=y} \mathsf {sx}[t]$. This optimization is certainly useful for long traces, because it minimizes the number of multiplications (precisely, only 2^m multiplications are done). However, we need 2^m temporary accumulators to save the s x ^′[y].

For monosample traces, we can also use this simpler computation:

$$\begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{m} x_{i} y_{i} &=& \sum\limits_{t} \sum\limits_{i / t_{i}=t} x_{i} \varphi(f(k,t_{i})) \\ &=& \sum\limits_{t} \sum\limits_{i / t_{i}=t} \varphi(f(k,t_{i})) x_{i} \\ &=& \sum\limits_{t} \varphi(f(k,t_{i})) \sum\limits_{i / t_{i}=t} x_{i} \\ &=& \sum\limits_{t} \varphi(f(k,t_{i})) \mathsf{sx}[t] . \end{array} $$

5.2 Fast computation of MIA

We setup a structure for the PMF, namely an array of hash tables, denoted as P M F[t][x], where t and x lie in the sets ${\mathbb F_{2}^{n}}$ and I m(φ ∘ f) + s u p p(N), respectively. Suppose we have accumulated $\tilde {q}$ leakage pairs (t,x).

At this stage, the joint probability is given by

$$\tilde{\mathbb{P}}(t,x) = \frac{1}{\tilde{q}} \mathsf{PMF}[t][x] . $$

Now, when using MIA as a distinguisher, we need to compute P M F[y][x], where $y{\in \mathbb {F}_{2}^{n}}$ (expecting the (t,k)↦y = φ(f(k,t)) function to be non-injective [24], which is the case in the previous sections). The value P M F[y][x] implicitly depends upon a key guess k: P M F[y][x] = P M F[y = φ(f(k,t))][x]. Now, instead of computing $\tilde {\mathbb {P}}(x,y)$ through P M F[y][x] explicitly for each key guess, we can reformulate

$$\tilde{\mathbb{P}}(y,x) = \sum\limits_{t} \tilde{\mathbb{P}}(t,y,x) = \sum\limits_{t / \varphi(f(k,t))=y} \tilde{\mathbb{P}}(t,x) = \frac{1}{\tilde{q}} \sum\limits_{t / \varphi(f(k,t))=y} \mathsf{PMF}[t][x] . $$

Thus, we can reuse the tabulated P M F[t][x] for each key guess, which requires thus much less computations than a straightforward implementation.

Recall the expression of the estimated mutual information:

$$\tilde I(\tilde{\mathbf{x}},\tilde{\mathbf{y}}) = \sum\limits_{x,y} \tilde{\mathbb{P}}(x,y) \log_{2} \frac{\tilde{\mathbb{P}}(x,y)}{\tilde{\mathbb{P}}(x)\,\tilde{\mathbb{P}}(y)} . $$

The value for $\tilde {\mathbb {P}}(x)$ is identical for all key hypotheses and thus can be factored out. In fact, this quantity is a scaling constant which could be omitted. But for the sake of completeness, we have

$$\tilde{\mathbb{P}}(x) = \sum\limits_{t} \tilde{\mathbb{P}}(t,x) = \frac{1}{\tilde{q}} \sum\limits_{t} \mathsf{PMF}[t][x] . $$

Lastly, we need to evaluate $\tilde {\mathbb {P}}(y)$. This is simply done as follows:

$$\tilde{\mathbb{P}}(y) = \sum\limits_{x} \tilde{\mathbb{P}}(x,y) . $$

Algorithm 1 illustrates the fast computation process for MIA while Algorithm 2 computes the success rate of MIA. Algorithm 2 calls the function MIA-Distinguisher as a subroutine. This last function corresponds to the of the computation of fast MIA (Algorithm 1). However, it is optimized as follows:

• The values of $\tilde {\mathbb {P}}(x)$ and $\tilde {q}$ do not impact the result, hence they are not computed. This means that lines 4–8 of Algorithm 1 are not part of Algorithm MIA-Distinguisher, and that in the accumulation of $\tilde {I}(\tilde {\mathbf {x}},\tilde {\mathbf {y}}(k))$ at line 15 of Function MIA-Distinguisher, the terms $\tilde {\mathbb {P}}(x)$ and $\tilde {q}$ (present at line 25 of Algorithm 1), are simply dropped.

• In the line 17 of MIA-Distinguisher, we subtract the term which corresponds to the denominator $\tilde {\mathbb {P}}(y)$ of line 25 of Algorithm 1. Notice that all the parameters of the logarithms are now integers. We can thus tabulate the logarithms in a table log [i], for $i=1, \ldots , \tilde {q}$. Incidentally, the basis of the logarithm can be arbitrarily chosen. If $\tilde {q}$ is really large, say larger than 10 millions, then log [i] can be precomputed from all i < 10⁶, and evaluated otherwise, since anyhow the call of log for large values is restricted to the case of $\tilde {\mathbb {P}}(y)$ which is expected to be way larger than any $\tilde {\mathbb {P}}(x,y)$.

5.3 Standard computation algorithm for MIA

The standard computation for MIA unfolds as in Algorithm 3. This algorithm outputs exactly the same as Algorithm 1 but is slower for two reasons:

• 1. All the $\tilde {q}$ samples are scanned for each key hypothesis;

• 2. Probability mass functions are normalized. Now, divisions are costly, and also they require a conversion from integer to floating point numbers;

6 Conclusion

We derived MIA anew as the distinguisher which maximizes the success rate when the exact probabilities are replaced by online estimations. This suggests that MIA is an interesting alternative when the attacker is not able to exactly determine the link between the measured leakage and the leakage model. This situation can either result from an unknown deterministic part or from an unknown noise distribution. We have proved that, if the number of traces is greater than the number of possible values of x and y, the MIA is faster in terms of logarithm computations.

We have presented two practical case-studies in which MIA can indeed be more efficient than CPA or LRA. The first scenario is for non-Gaussian noise but known deterministic leakage model. The second scenario is for Gaussian noise with unknown deterministic leakage model, where one leverages a challenging leakage function which results in failure for CPA, and in harsh regression using LRA. Incidentally, this example is in line with the work carried out by Whitnall and Oswald [21] where a notion of relative margin is used to compare attacks. Our findings go in the same direction using the success rate as a figure of merit to compare attacks.

Finally, we extended the computation trick given for CPA to MIA avoiding the histogram estimation of conditional probabilities for each sub key individually, improving the speed of the computation.

We note that all our results are φ-dependent. It seems obvious that the closer we are to the actual leakage, the better the success rate will be. An open question is to find an analytic way to determine the function model that will provide the highest success rate.

Last, we note that our analysis is monovariate: we consider a leakage which consists in only one value. A future work would be to extend our results to mutivariate attacks.

Another topic of research is to carry out practical examples where MIA beats CPA. An viable option would be the exploitation of some specific timing attacks where the behaviour of the processor changes at every start-up.