Introduction

Populations can experience increased mortality due to habitat loss, harvest, exposure to parasites or pathogens and other changes in their environment. Understanding how populations respond to increased mortality is important for developing and applying conservation biology and population management strategies. The intuition underlying many of these strategies may be that increased mortality of a species leads to decreased abundance and biomass of all life-history stages of a species.

However, increased mortality of a species can have the counterintuitive effect of causing an increase in the abundance of one or more life-history stages. Increased abundance of one or more stages in response to increased mortality of a single stage is known as stage-specific overcompensation in (numerical) density (hereafter, overcompensation in density). Overcompensation in density has been observed in empirical studies of fish (Smith et al. (1996); Reznick, Butler IV and Rodd (2001); Zipkin, Sullivan and Cooch et al. (2008); Cameron and Benton (2004); Meyer, Lamansky and Schill (2006); Persson, Amundsen and de Roos et al. (2007); Weidel, Josephson and Kraft (2007)), insects (Watt (1955); Nicholson (1957); Smallegange, Fernandes and Croll (2018)) and crustaceans (Slobodkin and Richman (1956)). In addition, in some studies the increase in density of one or more stages offsets the decreases in densities of the other stages and the total population density increases with increased mortality (Watt (1955); Slobodkin and Richman (1956); Smith et al. (1996); Meyer, Lamansky and Schill (2006); Zipkin, Sullivan and Cooch et al. (2008)). Increases in the total population density in response to (possibly stage-specific) mortality are called hydra effects (Abrams and Matsuda (2005); Abrams (2009)).

Current theory predicts many mechanisms that can cause hydra effects in unstructured populations, but there is limited theory on the mechanisms driving overcompensation in density and hydra effects in stage-structured populations. Mechanisms causing hydra effects in multi-species models of unstructured populations include subsystem instability (i.e., positive feedbacks between species that destabilize subsets of the community; Cortez and Abrams 2016; Cortez 2016), prudent resource exploitation (i.e., consumer per capita consumption rates decrease with increasing mortality; Abrams 2009), changes in cycle amplitude for systems exhibiting population oscillations (Abrams, Brassil and Holt (2003); Abrams (2009); Sieber and Hilker (2012)), and adaptation of one or more species (Abrams and Vos (2003); Abrams and Matsuda (2005); Abrams (2019); Cortez and Yamamichi (2019)). For stage-structured populations, overcompensation in density and hydra effects are predicted to occur when there is temporal separation of mortality and density dependence such that one stage experiences increased mortality and there is overcompensation in the maturation or reproduction rate of a different stage (i.e., increased density of a stage decreases the maturation rate or reproductive output from that stage) (de Roos, Persson and Thieme (2003); Abrams (2009)). It is expected that the mechanisms for hydra effects listed above can cause overcompensation in density and hydra effects in stage-structured populations as well, but it is unknown if there are other mechanisms that also cause the two phenomena in stage-structured populations.

Insight into additional possible mechanisms may be gained by looking at the body of theory on a closely related phenomena known as stage-specific overcompensation in biomass (hereafter, overcompensation in biomass). Overcompensation in biomass occurs when increased mortality of one stage results in increased biomass of one or more stages. Current mathematical theory predicts that overcompensation in biomass is caused by bottleneck life stages (i.e., life stages where the population growth is most regulated; de Roos, Schellekens and van Kooten et al. 2007; de Roos and Persson 2013), ontogenetic asymmetry (wherein an individual’s response to resource density or the mortality it experiences differs based on its current life-history stage; Persson and de Roos 2013), and overcompensation in an ecological rate (de Roos, Schellekens and van Kooten et al. (2007); Karatayev, Kraft and Zipkin (2015)). An important property of biomass-based models is that they account for increases and decreases in biomass in each life-history stage due to somatic growth. Somatic growth is not incorporated into the models of unstructured populations or the models of stage-structured populations used in the above studies on overcompensation in density and hydra effects. Because of this, it is unclear when the mechanisms driving overcompensation in biomass also cause overcompensation in density and hydra effects.

Altogether, overcompensation in density, overcompensation in biomass and hydra effects are related phenomena, but we have a limited understanding of how the mechanisms driving the different phenomena are related. Our goal in this study is to help fill in one gap in the existing body of theory by identifying the biological and mathematical mechanisms that drive overcompensation in density and hydra effects in single-species systems. Our work focuses on finding the conditions under which the two phenomena occur at stable equilibria of an n-stage single-species model that describes the changes in density (as opposed to biomass) in each stage. We also use the model to assess whether predictions from previous studies using density-based models and biomass-based models hold for density-based single-species models with an any number of stages. The specific prediction from density-based models (Abrams (2009)) is that (i) overcompensation in the maturation or reproductive rate of one or more stages is a necessary requirement for overcompensation in density or a hydra effect to arise at a stable equilibrium. We show that overcompensation in a rate is a necessary condition for density-based two-stage models, but not necessary for density-based models with three or more stages. The predictions from biomass-based models (e.g., de Roos, Schellekens and van Kooten et al. 2007) are (ii) sufficiently strong intraspecific competition that causes overcompensation in the maturation or reproductive rate of one stage can cause stage-specific overcompensation in biomass in any other stage and (iii) a single stage cannot experience both overcompensation in its maturation rate and increased biomass in response to an increase in its own mortality rate. We show that prediction (ii) applies to overcompensation in density in our model, but counter to prediction (iii), it is possible for a single stage to simultaneously experience overcompensation in its maturation rate and overcompensation in density in response to its own mortality rate. Overall, our work helps clarify the relationships between intra-stage and inter-stage competition, overcompensation in ecological rates, overcompensation in density and hydra effects in single-species models. It also points toward future work on the relationships between those phenomena and overcompensation in biomass.

Models and Methods

Single-species n-stage model

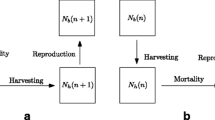
Our model describes the dynamics of a single species with n life-history stages. The density of each stage is denoted by \(N_i\) (\(1\le i \le n\)). We assume that all individuals are born into the first stage, all stages experience density-independent mortality, and only individuals in stage n reproduce. We also allow for the possibility that individuals compete for resources with other individuals that are in the same stage and other stages. These assumptions qualitatively match the life histories of many organisms (e.g., insect species) and align with the assumptions made in previous studies that use density-based stage-structured models (de Roos, Persson and Thieme (2003); Schreiber and Rudolf (2008); Abrams (2009); de Roos (2018)). We note that because our model focuses on (numerical) densities and not biomass (e.g., as in de Roos 2018; de Roos and Persson 2013; Karatayev, Kraft and Zipkin 2015), our model does not account for how the biomass of individuals in a given stage can change due to somatic growth, a point we return to in the Discussion.

The n-stage model is

$$\begin{aligned} \frac{dN_1}{dt}= & {} N_nb(N_1,N_2,\ldots , N_n) \nonumber \\&- N_1g_1(N_1,N_2,\ldots , N_n) - m_1N_1 \nonumber \\ \frac{d N_i}{dt}= & {} N_{i-1}g_{i-1}(N_1,N_2,\ldots , N_n) \nonumber \\&- N_ig_i(N_1,N_2,\ldots , N_n) - m_iN_i, \quad 2 \le i \le n-1 \nonumber \\ \frac{dN_n}{dt}= & {} N_{n-1}g_{n-1}(N_1,N_2,\ldots , N_n) - m_nN_n \end{aligned}$$
(1)

where \(m_i\) is the per capita mortality rate of stage i, \(b(N_1,N_2,\ldots , N_n)\) is the adult reproductive rate, and \(g_i(N_1,N_2,\ldots , N_n)\) is the rate at which individuals mature from stage i to stage \(i+1\). For each stage, the input rate is the maturation rate from the previous stage (stages \(i>1\)) or the adult reproduction rate (stage \(i=1\)). The output rate is the sum of the maturation rate (stages \(i<n\)) and mortality rate (all stages).

Competition between individuals in the same stage (intra-stage competition) and different stages (inter-stage competition) is accounted for in the maturation and reproductive rates of each stage. Competition within and between stages can be due to exploitative competition or interference competition. When inter-stage competition is absent, e.g., each stage has a different resource, the adult reproductive rate only depends on adult density, \(N_nb(N_1,N_2, \ldots ,N_n) = N_nb(N_n)\), and the maturation rate of stage i only depends on the density of individuals in stage i, \(N_ig_i(N_1,N_2, \ldots ,N_n) = N_ig_i(N_i)\). When inter-stage competition is present, the reproductive and maturation rates also depend on some or all of the densities of other stages. In all cases, we assume the functions b and \(g_i\) are decreasing functions of their arguments, e.g., \(\frac{\partial g_i}{\partial N_j} < 0\), where stronger competition implies values that are larger in magnitude. In Online Resource S1.1 and S1.2, we show that previous resource-explicit models with and without exploitative competition between stages (Schreiber and Rudolf (2008); Abrams (2009); de Roos (2018)) can be converted into the resource-implicit form of model (1) using a separation of time scales argument. Moreover, because all of our results focus on stable equilibria, all of our results for the resource-implicit model (1) apply to the resource-explicit models in those studies.

Jacobian, hydra effects and overcompensation in rates and biomass

Our analysis focuses on how the equilibrium densities respond to a change in the per capita mortality rate of one stage. Because of this, we assume model (1) has a (linearly) stable equilibrium point, \(\rho = (N_1^*,...,N_n^*)\), where all stages have nonzero densities. Equilibrium stability is determined by the Jacobian,

$$\begin{aligned} J|_{\rho }= & {} \left. \begin{bmatrix} J_{11} &{} J_{12} &{} \ldots &{} J_{1n} \\ J_{21} &{} J_{22} &{} \ldots &{} J_{2n} \\ J_{31} &{} J_{32} &{} \ldots &{} J_{3n} \\ \vdots &{} \vdots &{} \ldots &{} \vdots \\ J_{n1} &{} J_{n2} &{} \ldots &{} J_{nn} \end{bmatrix}\right| _{\rho }\nonumber \\= & {} \left. \begin{bmatrix} \frac{\partial }{\partial N_1}\frac{dN_1}{dt} &{} \frac{\partial }{\partial N_2}\frac{dN_1}{dt} &{} \ldots &{} \frac{\partial }{\partial N_n}\frac{dN_1}{dt} \\ \frac{\partial }{\partial N_1}\frac{dN_2}{dt} &{} \frac{\partial }{\partial N_2}\frac{dN_2}{dt} &{} \ldots &{} \frac{\partial }{\partial N_n}\frac{dN_2}{dt} \\ \vdots &{} \vdots &{} \ldots &{} \vdots \\ \frac{\partial }{\partial N_1}\frac{dN_n}{dt} &{} \frac{\partial }{\partial N_2}\frac{dN_n}{dt} &{} \ldots &{} \frac{\partial }{\partial N_n}\frac{dN_n}{dt} \end{bmatrix}\right| _{\rho }. \end{aligned}$$
(2)

If all eigenvalues of the Jacobian have negative real parts, then the equilibrium is stable. If one or more eigenvalues of the Jacobian has a positive real part, then the equilibrium is unstable.

Entry \(J_{ij}\) of the Jacobian describes how changes in the density of stage j affect the dynamics of stage i. Biologically, entries on the diagonal (\(J_{ii}\)) describe the effects of intra-stage competition in stage i on the maturation rate of stage i, the effects of mortality in stage i, and the effects of inter-stage competition of stage i on its input rate. Entries on the subdiagonal (\(J_{i+1,i}\)) describe the effects of maturation from state i, the effects of intra-stage competition on the maturate rate of stage i, and the effects of inter-stage competition of stage i on the maturation rate of stage \(i+1\). Similarly, the top-right entry, \(J_{1n}\), describes the effects of reproduction, the effects of intra-stage competition in stage n on the reproduction rate, and the effects of inter-stage competition of stage n on the maturation rate of stage 1. All other entries (\(J_{ij}\)) describe the effects of inter-stage competition of stage j on the input and output rates of stage i. In the special case of no inter-stage competition, only the diagonal, subdiagonal and top-left entries have nonzero values.

We can also interpret the Jacobian entries and products of Jacobian entries in terms of the direct and indirect effects one stage has on the dynamics of each stage. Specifically, \(J_{ij}\) describes the direct effect stage j has on the dynamics of stage i; the product \(J_{ik}J_{kj}\) describes the indirect effect stage j has on the dynamics of stage i mediated by stage k; \(J_{il}J_{lk}J_{kj}\) describes the indirect effect stage j has on the dynamics of stage i mediated by stage k and l; and so forth.

Our results about mortality perturbations involve signed direct and indirect effects. Signed direct and indirect effects are (products of) Jacobian entries that have been multiplied by the factor \((-1)^m/|J|\), where |J| is the determinant of the Jacobian and the value of the integer m is determined by the particular response being computed using equation (3); see the next subsection. A signed direct and indirect effect is positive and negative when the value of \((-1)^m/|J|\) times the indirect effect is positive and negative, respectively. For example, the signed direct effect \((-1)^mJ_{21}/|J|\) is positive when \((-1)^mJ_{21}/|J|>0\) and negative when \((-1)^mJ_{21}/|J|<0\). Similarly, the signed indirect effect \((-1)^mJ_{23}J_{31}/|J|\) is positive when \((-1)^mJ_{23}J_{31}/|J|>0\) and negative when \((-1)^mJ_{23}J_{31}/|J|<0\).

Defining overcompensation in an ecological rate, overcompensation in density and hydra effects at stable equilibria

Terms within the Jacobian entries and products of the Jacobian entries define whether overcompensation in a maturation or reproductive rates, stage-specific overcompensation in density and hydra effects occur at a stable equilibrium. In general, overcompensation in an ecological rate (at equilibrium) occurs when stage i has reduced output with increased input. More specifically, overcompensation in the maturation or reproductive rate of stage i occurs when increased density of stage i results in a reduced maturation or reproductive rate of stage i. Mathematically, overcompensation in the maturation rate of stage i is defined by \(N_i^* \frac{\partial g_i}{\partial N_i}+g_i\Big |_{\rho }<0\) and overcompensation in the reproductive rate of stage n is defined by \(N_n^* \frac{\partial b}{\partial N_n}+b\Big |_{\rho }<0\). Overcompensation in rates affects the signs of the diagonal, subdiagonal and top-right entries of the Jacobian.

Stage-specific overcompensation in density of stage i occurs (at equilibrium) when increased mortality of stage j results in increased density of stage i. Mathematically, overcompensation in density is defined by the partial derivative \(\frac{\partial N_i^*}{\partial m_j} > 0\). Following Bender, Case and Gilpin (1984), Yodzis (1988), Novak, Wootton and Doak et al. (2011), and Cortez and Abrams (2016), the partial derivatives are computed using the Jacobian via the equation,

$$\begin{aligned} \frac{\partial N_i^*}{\partial m_j} = (-1)^{i+j}\frac{N_j^*}{|J|}|M_{ji}| \end{aligned}$$
(3)

where \(|M_{ji}|\) is the j, i-minor of the Jacobian, i.e., the determinant of the submatrix of the Jacobian where row j and column i have been removed. Note that because the minors are defined by products and sums of the entries of the Jacobian, the minors can be interpreted in terms of signed direct and indirect effects between the stages.

Finally, increased mortality of a single stage can cause the total equilibrium density of a population to increase. Increased total density with increased mortality is called a hydra effect (Abrams and Matsuda (2005); Abrams (2009)) and mathematically defined by \(\sum _i\frac{\partial N_i^*}{\partial m_j} >0\).

Results

Stage-specific overcompensation in density in two-stage models

First consider the case of \(n=2\) stages, where \(N_1\) is the density of juveniles and \(N_2\) is the density of adults. The Jacobian for the two-stage model is

$$\begin{aligned} J|_{\rho } = \left.\begin{bmatrix} N_2\frac{\partial b}{\partial N_1} - m_1 - \left( N_1\frac{\partial g}{\partial N_1} + g(N_1,N_2)\right) &{} b(N_1,N_2) + N_2\frac{\partial b}{\partial N_2} - N_1\frac{\partial g}{\partial N_2}\\ g(N_1,N_2) + N_1\frac{\partial g}{\partial N_1} &{} N_1\frac{\partial g}{\partial N_2} - m_2 \end{bmatrix}\right |_{\rho }. \end{aligned}$$
(4)

where \(|J| > 0\) when evaluated at a stable equilibrium. In the two-stage system, overcompensation in juvenile maturation rate occurs when the maturation rate decreases with juvenile density (\(N_1\frac{\partial g_1}{\partial N_1} + g_1 \Big |_{\rho }< 0\)) and overcompensation in the adult reproductive rate occurs when reproductive rate decreases with adult density (\(N_2\frac{\partial b}{\partial N_2} + b \Big |_{\rho }< 0\)).

The changes in densities in response to an increase in either mortality rate are given by

$$\begin{aligned} \frac{\partial N_1^*}{\partial m_1}= & {} \frac{N_1}{|J|}\left( N_1\frac{\partial g_1}{\partial N_2} - m_2\right) \Biggr |_{\rho } \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial N_1^*}{\partial m_2}= & {} \frac{-N_2}{|J|}\Biggr (\overbrace{b(N_1,N_2) + N_2\frac{\partial b}{\partial N_2}}^{\begin{array}{c} \text {terms defining overcompensation}\\ \text { in adult reproductive rate} \end{array}} - N_1\frac{\partial g_1}{\partial N_2}\Biggr )\Biggr |_{\rho } \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial N_2^*}{\partial m_1}= & {} \frac{-N_1}{|J|}\overbrace{\left( g_1(N_1,N_2) + N_1\frac{\partial g_1}{\partial N_1}\right) }^{\begin{array}{c} \text {terms defining overcompensation}\\ \text { in juvenile maturation rate} \end{array}}\Biggr |_{\rho } \end{aligned}$$
(7)
$$\begin{aligned} \frac{\partial N_2^*}{\partial m_2}= & {} \frac{N_2}{|J|}\biggr (N_2\frac{\partial b}{\partial N_1} - m_1 \overbrace{-\left[ N_1\frac{\partial g_1}{\partial N_1} + g_1(N_1,N_2)\right] }^{\begin{array}{c} \text {terms defining overcompensation}\\ \text { in juvenile maturation rate} \end{array}}\biggr )\Biggr |_{\rho } \end{aligned}$$
(8)

Two-stage models without inter-stage competition

When there is no inter-stage competition, e.g., each stage uses a separate resource, the derivatives \(\partial g_1/\partial N_2\) and \(\partial b/\partial N_1\) are zero. Equations (5)-(8) reveal that overcompensation in density of stage i can only occur if intra-stage competition in stage j (\(j \ne i\)) is strong enough that it causes sufficiently strong overcompensation in the maturation or reproduction rate of stage j. Specifically, overcompensation in adult density in response to increases in either mortality rate can occur only if intra-stage competition in the juvenile stage is strong enough that it causes sufficiently large overcompensation in the juvenile maturation rate (i.e., \(g_1 + N_1 \frac{\partial g_1}{\partial N_1}\Big |_{\rho }\) is negative and sufficiently large in magnitude). Overcompensation in juvenile density in response to increased adult mortality can occur only if intra-stage competition in the adult stage is strong enough that it causes sufficiently large overcompensation in the adult reproductive rate (i.e., \(g_1 + N_1 \frac{\partial g_1}{\partial N_1}\Big |_{\rho }\) is negative and sufficiently large in magnitude).

Two-stage models with inter-stage competition

When there is inter-stage competition, e.g., there is overlap in resource use of the two stages, one or both of the derivatives \(\partial g_1/\partial N_2\) and \(\partial b/\partial N_1\) are negative. As in the previous case, overcompensation in density of stage i in response to an increase in mortality of any stage can occur only if intra-stage competition in stage j (\(j \ne i\)) is strong enough that it causes sufficiently strong overcompensation in the maturation or reproduction rate of stage j. The key difference is that the inter-stage competition terms inhibit overcompensation in density by requiring stronger amounts of intra-stage competition in order for overcompensation in density to occur. In total, our results show that in the two-stage model inter-stage competition inhibits overcompensation in density, intra-stage competition promotes overcompensation in density, and overcompensation in density can only occur if intra-stage competition is sufficiently strong that it causes overcompensation in the juvenile maturation or adult reproduction rate.

Figure 1 C,D shows examples where intra-stage competition in the juvenile stage is strong enough to cause overcompensation in the juvenile maturation rate and overcompensation in adult density (solid blue lines are increasing). Figure 1 F shows examples where intra-stage competition is strong enough to cause overcompensation in the adult reproductive rate and overcompensation in juvenile density (dashed red curves increasing). In all other panels, intra-stage competition is too weak to cause overcompensation in a rate and all densities decrease with increased mortality.

There are additional constraints on when overcompensation in density can occur. First, overcompensation in juvenile density in response to increased juvenile mortality is not possible in our model due to the assumption that adult per capita mortality is independent of adult density. However, if the adult per capita mortality is a decelerating function of adult density, e.g., \(m_2 = m_2(N_2)\) such that \(\frac{d}{d N_2}m_2<0\), then overcompensation in juvenile density in response to increased juvenile mortality can occur when the decelerating mortality rate causes \(J_{22}>0\). This is a form of overcompensation in the adult mortality rate wherein increased adult density results in decreased output of dead adults; see Online Resource S1.3 for details. Second, in order for the system to remain stable, overcompensation in the juvenile maturation rate and adult mortality rate (if it exists) must be sufficiently small in magnitude. Otherwise, the trace of the Jacobian is positive, which implies an unstable equilibrium.

Stage-specific overcompensation in density in three-stage models

We now focus on the case of \(n=3\) stages, where \(N_1\) is the density of small juveniles, \(N_2\) is the density of large juveniles, and \(N_3\) is the density of adults. The Jacobian for the three-stage model is

$$\begin{aligned} J|_{\rho } =\left. \begin{bmatrix} N_3\frac{\partial b}{\partial N_1} - (g_1 + N_1\frac{\partial g_1}{\partial N_1}) - m_1 &{} N_3\frac{\partial b}{\partial N_2} -N_1\frac{\partial g_1}{\partial N_2} &{} b + N_3\frac{\partial b}{\partial N_3} - N_1\frac{\partial g_1}{\partial N_3} \\ g_1 + N_1\frac{\partial g_1}{\partial N_1} - N_2\frac{\partial g_2}{\partial N_1} &{} N_1\frac{\partial g_1}{\partial N_2} - (g_2 + N_2\frac{\partial g_2}{\partial N_2}) - m_2 &{} N_1\frac{\partial g_1}{\partial N_3} - N_2\frac{\partial g_2}{\partial N_3} \\ N_2\frac{\partial g_2}{\partial N_1} &{} g_2 + N_2\frac{\partial g_2}{\partial N_2} &{} N_2\frac{\partial g_2}{\partial N_3} - m_3 \end{bmatrix} \right| _{\rho } \end{aligned}$$
(9)
Fig. 1
figure 1

In two-stage models, overcompensation in the density of stage i can only occur if intra-stage competition in stage j (\(j\ne i\)) is strong enough that it causes overcompensation in the maturation or reproductive rate of stage j. Each panel shows juvenile (dashed red) and adult (solid blue) densities as juvenile mortality (left column) or adult mortality (right column) is varied; overcompensation in density occurs when a curve is increasing. Rows show examples where (top) intra-stage competition is sufficiently weak that there is no overcompensation in any rate, or intra-stage competition is sufficiently strong that there is overcompensation in the (middle) juvenile maturation rate or (bottom) adult reproductive rate. (A,B) Overcompensation in density is impossible in the absence of overcompensation in any rate. (C,D) Overcompensation in adult density in response to increased mortality of either stage occurs if there is sufficiently strong overcompensation in the juvenile maturation rate. (E,F) Overcompensation in juvenile density can only occur in response to increased adult mortality and only if there is sufficiently strong overcompensation in the adult reproductive rate. See Online Resource S4 for model equations and parameters

Full size image

where \(|J| < 0\) when evaluated at a stable equilibrium. The equations defining how the densities respond to an increase in the mortality of each stage are given in Online Resource S2.

Three-stage models without inter-stage competition

We first consider systems where there is no inter-stage competition, i.e., when each stage has a separate resource (left column of Figure 2). Equations (S.8) in Online Resource S2.1 show that overcompensation in density of stage i in response to an increase in the mortality of stage j can only occur if (i) intra-stage competition in stage k (\(k\ne i\)) is strong enough that it causes sufficiently strong overcompensation in the maturation rate of stage k or (ii) \(j>i\) and intra-stage competition in the adult stage is strong enough that it causes sufficiently strong overcompensation in the adult reproductive rate. These predictions are identical those in de Roos, Persson and Thieme (2003).

Specifically, overcompensation in adult density in response to any mortality rate can only occur if intra-stage competition in one of the juvenile stages is strong enough that it causes sufficiently large overcompensation in one juvenile maturation rate (panel E of Figure 2). Figure 3 D-I shows examples where intra-stage competition in one of the juvenile stages is sufficiently strong to cause overcompensation in adult density, and Figure 3 A-C,J-L shows examples where overcompensation in adult density does not occur because intra-stage competition in both juveniles stages is weak.

For the juvenile stages, overcompensation in density can occur if intra-stage competition in the other juvenile stage is sufficiently strong that it causes overcompensation in the maturation rate of that stage (blue arrows in Figure 2 A,C). Overcompensation in small juvenile density also can occur if intra-stage competition between adults is sufficiently strong that it causes overcompensation in the adult reproduction rate (red arrows in Figure 2 A). Figure 3 G-I, K,L and Figure 3 D-F, L show examples where intra-stage competition is sufficiently strong to cause overcompensation in small juvenile density and large juvenile density, respectively. When intra-stage competition is sufficiently weak in all stages such that no stage experiences overcompensation in a rate, then all densities decrease with an increase in any mortality rate (Figure 3 A-C). Also, overcompensation in density of a given stage cannot occur in response to increases in the mortality rate of that stage (decreasing red dashed lines in column 1 and decreasing magenta dash-dot lines in column 2).

Three-stage models with inter-stage competition

We now consider systems where inter-stage competition between some or all stages is present. Overcompensation in density of stage i in response to an increase in the mortality of stage j can occur only if (i) intra-stage competition in stage k (\(k\ne i\)) is strong enough that it causes sufficiently large overcompensation in the maturation rate of stage k, (ii) \(j>1\) and intra-stage competition in the adult stage is strong enough that it causes sufficiently strong overcompensation in the adult reproductive rate, or (iii) there is sufficiently strong inter-stage competition between the other two stages. We focus on the two effects inter-stage competition has on overcompensation in density: (1) inter-stage competition inhibits overcompensation in density by inhibiting the mechanisms in conditions (i) and (ii) and (2) inter-stage competition causes overcompensation in density via condition (iii). To help explain this, we use the response of stage 2 to increases in mortality in stage 3,

$$\begin{aligned} \frac{\partial N_2^*}{\partial m_1} = \frac{-N_1}{|J|}\Biggr [&\overbrace{\bigg (N_3\frac{\partial b}{\partial N_1} - g_1-N_1\frac{\partial g_1}{\partial N_1}-m_1\bigg )}^{\begin{array}{c} \text {terms defining overcompensation in stage 1}\\ \text { maturation rate and inter-stage competition} \end{array}} \overbrace{\bigg (N_1\frac{\partial g_1}{\partial N_3}-N_2\frac{\partial g_2}{\partial N_3}\bigg )}^{\begin{array}{c} \text {terms defining}\\ \text {inter-stage competition} \end{array}} \nonumber \\&- \underbrace{\bigg (g_1+N_1\frac{\partial g_1}{\partial N_1}-N_2\frac{\partial g_2}{\partial N_1}\bigg )}_{\begin{array}{c} \text {terms defining overcompensation in stage 1 }\\ \text { maturation rate and inter-stage competition} \end{array}} \,\,\underbrace{\bigg (b+ N_3\frac{\partial b}{\partial N_3}- N_1\frac{\partial g_1}{\partial N_3}-m_3\bigg )}_{\begin{array}{c} \text {terms defining overcompensation in }\\ \text {reproductive rate and inter-stage competition} \end{array}}\Biggr ]\Biggr|_\rho. \end{aligned}$$
(10)

Additional details about other responses are given in Online Resource S2.1.

The first effect of inter-stage competition is that it inhibits overcompensation in density being driven by intra-stage competition. For overcompensation in density of stage i to occur via conditions (i) and (ii), intra-stage competition in stage k (\(k\ne i\)) needs to be strong enough to cause overcompensation in the output rate of stage k (left column of Figure 2, but all or some stages compete for resources). The amount of intra-stage competition needed to get overcompensation in density increases if stage k has strong inter-stage competitive effects on its own input rate or the output rate of stage \(k+1\). Both inhibitory effects can be seen in equation (10). In the first line of equation (10), the first set of parentheses contains terms defining overcompensation in the maturation rate of stage 1 and the inter-stage competitive effects of stage 1 on its input rate (i.e., the adult reproductive rate; \(N_3\partial b/\partial N_1\)). These terms have opposite signs when there is overcompensation in the maturation rate of stage 1. This means overcompensation in density of stage 2 requires greater amounts of intra-stage competition in stage 1 when stage 1 has inter-stage competitive effects on its input rate. In the second line of equation (10), the first set of parentheses contains terms defining overcompensation in the maturation rate of stage 1 and the inter-stage competitive effects of stage 1 on the output rate of stage 2 (i.e., the maturation rate of stage 2; \(N_2\partial g_2/\partial N_1\)). These terms have opposite signs when there is overcompensation in the maturation rate of stage 1. This means overcompensation in density of stage 2 requires greater amounts of intra-stage competition in stage 1 when stage 1 has inter-stage competitive effects on the output rate of stage 2. A similar effect is seen in the second set of parentheses on the second line of equation (10). In total, as in the two-stage model, inter-stage competition inhibits overcompensation in density that is driven by strong intra-stage competition.

Fig. 2
figure 2

Illustration of the ways intra-stage and inter-stage competition for resources can lead to overcompensation in density in the three-stage model. In all panels, arrows between numbered boxes denote maturation or reproduction and arrows from resources (black rectangles) to numbered squares denote resource use. For simplicity, the effects of intra-stage competition are illustrated in the scenario where each stage has a separate resource and the effects of inter-stage competition are illustrated in the scenario where pairs of stages share resources; all effects are present if all stages use the same resource. Dashed arrows mean that there is overcompensation in the reproduction or maturation rate. Thick resource-use arrows denote that a given stage has strong competitive effects on all stages (including itself) that use the same resources. Arrow colors show which maturation or reproduction rate is affected by the strong competitive interactions. Left column: Overcompensation in density of stage i can be driven by intra-stage competition in stage j (\(j\ne i\)) that is sufficiently strong to cause overcompensation in the maturation or reproduction rate of stage j (red or blue arrows). Right column: Overcompensation in density of stage i can be driven by sufficiently strong inter-stage competition between the other two stages that affects (blue arrows) the input rate for stage i or (red arrows) the input rate for the stage prior to stage i

Full size image
Fig. 3
figure 3

In three-stage models without inter-stage competition, overcompensation in stage i density can only occur if sufficiently strong intra-stage competition causes overcompensation in the maturation or reproductive rate of another stage. Each panel shows small juvenile (dashed red), large juvenile (dash-dot magenta) and adult (solid blue) densities as small juvenile mortality (left column), large juvenile mortality (middle column) or adult mortality (right column) is varied; overcompensation in density occurs when a curve is increasing. Rows show examples where (first) intra-stage competition is sufficiently weak that there is no overcompensation in any rate, or intra-stage competition is sufficiently strong that there is overcompensation in the (second) small juvenile maturation rate, (third) large juvenile maturation rate, or (fourth) adult reproductive rate. (A-C) Stage-specific overcompensation in density is impossible in the absence of overcompensation in any rate. (D-F) Overcompensation in large juvenile or adult density in response to increased mortality of any stage occurs if there is sufficiently strong overcompensation in the small juvenile maturation rate. (G-I) Overcompensation in small juvenile or adult density in response to increased mortality of any stage occurs if there is sufficiently strong overcompensation in the large juvenile maturation rate. (J-L) Overcompensation in small juvenile density in response to increased large juvenile or adult mortality and overcompensation in large juvenile density in response to increased adult mortality occurs if there is sufficiently strong overcompensation in the adult reproductive rate. See Online Resource S4 for model equations and parameters

Full size image

The second effect of inter-stage competition is it can cause overcompensation in density, even in the absence of strong intra-stage competition. In this case, overcompensation in the density of stage i is caused by sufficiently strong inter-stage competition between the other two stages (right column of Figure 2, which is presented in the simple case where only pairs of stages compete for resources). The specific inter-specific competitive effects that can cause overcompensation in density are captured in entries \(J_{12}\), \(J_{23}\) and \(J_{31}\). We denote these three entries by \(J_{j, j+1}\), where it is understood that for \(j=3\), we interpret \(j+1\) as 1. Biologically, entry \(J_{j, j+1}\) represents the difference of the competitive effects stage \(j+1\) has on the input rate of stage j and the output rate of stage j. For example, \(J_{23}\) represents the difference between the competitive effect stage 3 has on the maturation rate of stage 1 (\(N_1\frac{\partial g_1}{\partial N_3}\); the input rate for stage 2) and the competitive effect stage 3 has on the maturation rate of stage 2 (\(N_2\frac{\partial g_2}{\partial N_3}\); the output rate for stage 2); see terms in the second set of parentheses on line 1 of equation (10). Biologically, entries of the form \(J_{j, j+1}\) will be large in magnitude when two stages have strong negative effects on each other (e.g., \(J_{23}\) can be large in magnitude if there is strong competition for resources between stages 2 and 3) or there is asymmetric competition such that one stage has strong negative effects on the other but the reverse effect is weak (e.g., \(J_{23}\) can be large in magnitude when adults strongly compete with large juveniles, but large juveniles have a small effect on adults).

There are two ways in which inter-stage competition can cause overcompensation in density in the absence of overcompensation in any rate. In the first case, one of the \(J_{j, j+1}\) entries is negative and large in magnitude (blue arrows in column 2 of Figure 2). Biologically, this means that the competitive effects stage \(j+1\) has on the input rate of stage j are sufficiently larger than the competitive effects stage \(j+1\) has on the output rate of stage j. For example (blue arrows in Figure 2 b), if large juveniles compete with adults for resources and do not compete with small juveniles, then the competitive effects of the large juveniles on adult reproductive rate (input for small juveniles) are larger than the competitive effects of large juveniles on the small juvenile maturation rate (output of small juveniles). This results in \(J_{12}<0\). The first row of Figure 4 shows examples of stage-specific overcompensation in density that arise when the competitive effects of all stages on input rates are stronger than the competitive effects on output rates (i.e., \(J_{j,j+1}<0\) for all j).

The second way inter-stage competition can cause overcompensation is density is defined by \(J_{12}\) or \(J_{23}\) being positive and sufficiently large in magnitude (red arrows in column 2 of Figure 2). Biologically, these conditions imply that stage \(j+1\) has stronger competitive effects on the output rate of stage j than the input rate of stage j. For example (red arrows in Figure 2 b), if adults compete with large juveniles for resources and do not compete with small juveniles, then the adults will have larger competitive effects on the maturation rate of large juveniles (output rate of large juveniles) than on the maturation rate of small juveniles (input rate of large juveniles). This results in \(J_{23}>0\), which would cause the terms in the second set of parentheses on line 1 of equation (10) to be positive. The second row of Figure 4 shows examples of stage-specific overcompensation in density that arise when the competitive effects of one stage on the output rate of another stage are stronger than the competitive effects on the input rate (i.e., \(J_{i,i+1}>0\) for one i). We note that in our numerical simulations, these examples only arose in small regions of parameter space and the magnitude of the increase in density was small.

Fig. 4
figure 4

In the three-stage model, overcompensation in density of stage i can be caused by sufficiently strong inter-stage competition between the other stages, even in the absence of overcompensation in any rate. Each panel shows small juvenile (dashed red), large juvenile (dash-dot magenta), and adult (solid blue) density as large juvenile mortality (left column), adult mortality (middle column), or small juvenile mortality (right column) is varied; overcompensation in density occurs when a curve is increasing with increased stage-specific mortality. Columns show examples where (left) \(J_{12}\), (middle) \(J_{23}\), and (right) \(J_{31}\) are large in magnitude. (A-C) The \(J_{ij}\) entries are negative and large in magnitude, meaning stage j has larger competitive effects on the input rate of state i than on the output rate of state i. (D-E) The \(J_{ij}\) entries are positive and large in magnitude, meaning stage j has larger competitive effects on the output rate of state i than on the input rate of state i. The effects in panels C-E are small and were only observed in small regions of parameter space. See Online Resource S4 for model equations and parameters

Full size image

In addition to causing overcompensation in density of a single stage, inter-stage competition allows for scenarios where all stages increase in density in response to increased mortality of one stage. Numerical examples of this phenomenon occurring in the absence of overcompensation in any rate are given in Online Resource S2.1. We note that in our numerical simulations, such examples only arise in small regions of parameter space due to the constraints imposed by the analytical conditions for overcompensation in density in all stages. Consequently, we do not expect this scenario to arise often in natural systems.

We note two additional constraints on when overcompensation in density can occur at a stable equilibrium of the three-stage model. First, overcompensation in the adult reproductive rate cannot cause stage-specific overcompensation in density (\(\partial N^*_i/\partial m_j\)) in the absence or presence of inter-stage competition if \(i \ge j\) or \(j=1\), respectively. However, if the adult per capita mortality rate is a decelerating function of adult density, e.g., \(m_3 = m_3(N_3)\) such that \(\frac{d}{dN_3}m_3 < 0\), then overcompensation in density of stage i can occur in response to increases in the mortality rate of any stage j. Second, in order for the system to remain stable, overcompensation in the small and large juvenile maturation rates and adult mortality rate (if it exists) must be sufficiently small in magnitude. Otherwise, the trace of Jacobian (9) will become positive, which implies an unstable equilibrium.

Stage-specific overcompensation in density in n-stage models

Here, we state conditions for stage-specific overcompensation in density for n-stage models that generalize the rules for the two-stage and three-stage models. We then interpret our results in terms of direct and indirect effects. Additional mathematical details are provided in Online Resource S3.

Conditions for stage-specific overcompensation in density

In systems where there is no inter-stage competition, e.g., each stage has a separate resource, overcompensation in density of stage i in response to an increase in the mortality of stage j can only occur if (i) intra-stage competition in stage k (\(k\ne i\)) is strong enough that it causes sufficiently large overcompensation in the maturation rate of stage k or (ii) \(j>i\) and intra-stage competition in the adult stage is strong enough that it causes sufficiently strong overcompensation in the adult reproductive rate. One other interesting property of systems without inter-stage competition is that if the levels of intra-stage competition are such that there is overcompensation in the maturation rate of at least one stage and no overcompensation in the reproductive rate of stage n, then increased mortality of any stage will cause overcompensation in density of multiple stages (mathematical details provided in proposition 4 of Online Resource S3.1). In particular, if there is sufficiently strong overcompensation in the maturation rate of an even number of stages, then increased mortality of any stage will cause overcompensation in the density of all stages that are experiencing overcompensation in their maturation rates. In contrast, if there is sufficiently strong overcompensation in the maturation rate of an odd number of stages, then increased mortality of any stage will cause overcompensation in the density of all stages that are not experiencing overcompensation in their maturation rates.

In systems where inter-stage competition is present, overcompensation in density of stage i in response to an increase in the mortality of stage j can occur if (i) intra-stage competition in stage k (\(k\ne i\)) is strong enough that it causes sufficiently large overcompensation in the maturation rate of stage k, (ii) \(j\ne 1\) and intra-stage competition in the adult stage is strong enough that it causes sufficiently strong overcompensation in the adult reproductive rate, or (iii) there is sufficiently strong inter-stage competition between some or all of the other stages. As pointed out for the three-stage model, inter-stage competition allows for the possibility that all stages increase in response to increased mortality of a single stage.

Interpreting conditions for overcompensation in density in terms of direct and indirect effects

Here, we show how our results about overcompensation in density can be interpreted in terms of signed direct and indirect effects between the stages. Recall from section 2.2 that signed direct and indirect effects are defined by (products of) the Jacobian entries that are multiplied by \((-1)^m/|J|\), for some integer m. We first discuss the specific direct and indirect effects defining \(\partial N_i^*/\partial m_i\), followed by the effects defining \(\partial N_i^*/\partial m_j\).

The sign of the change in density of stage i in response to increases in its own mortality rate (i.e., \(\partial N_i^*/\partial m_i\)) is determined by the sign of \(|M_{ii}|/|J|\). The submatrix \(M_{ii}\) has two interpretations: (i) \(M_{ii}\) defines all of the direct and indirect effects between all stages except for stage i and (ii) \(M_{ii}\) defines the stability of the equilibrium when the dynamics of stage i have been removed and the density of stage i is held fixed at its equilibrium density (i.e., \(N_i = N_i^*\); Cortez and Abrams 2016). This means that overcompensation in density of stage i in response to an increase in its own mortality rate is possible only if the sum of all signed direct and indirect effects between all stages except state i is positive, i.e., \(|M_{ii}|/|J|>0\). Interestingly, this shows that overcompensation in density of stage i in response to its own mortality is not driven by the dynamics of stage i or direct and indirect effects involving stage i, but instead driven by the dynamics and direct and indirect effects involving all other stages.

The sign of the change in density of stage i in response to increases in the mortality of stage j (i.e., \(\partial N_i^*/\partial m_j, j\neq i\)) is determined by the sign of \((-1)^{i+j}|M_{ij}|/|J|\). The determinant \(|M_{ij}|\) is the sum of three different kinds of terms that represent the direct and indirect effects of stage j on stage i, weighted by direct and indirect effects involving specific subsets of other stages. The first kind of term represents the indirect effect of stage j on stage i, mediated by changes in all of the other stages. Mathematically, it is defined by a string of direct effects connecting stage j to stage i that involves all of the other stages. For example, in a four-stage system, \(J_{13}J_{34}J_{42}\) is the indirect effect of stage 2 on stage 1, mediated by stages 3 and 4. The second kind of term represents the direct effect of stage j on stage i, weighted by all of the direct and indirect effects between the other stages. Mathematically, these terms are defined by the product of the direct effect of stage j on stage i and the determinant of the submatrix without the dynamics of stages i and j. For example, in a four-stage system, \(J_{12}(J_{34}J_{34}-J_{33}J_{44})\) is the product of the direct effect of stage 2 on stage 1 (\(J_{12}\)) and the determinant of the submatrix without the dynamics of stages 1 and 2 (i.e., just the dynamics of stages 3 and 4; \(J_{34}J_{34}-J_{33}J_{44}\)). The third kind of term represents the indirect effect of stage j on stage i mediated by some of the other stages and weighted by all of the direct and indirect effects between the remaining stages. Mathematically, these terms are defined by the product of (i) a string of direct effects that connects stage j to stage i that involves a subset of the other stages and (ii) the determinant of the submatrix without the dynamics of those stages. For example, in a four-stage system, \(J_{13}J_{32}J_{44}\) is the product of the indirect effect of stage 2 on stage 1 mediated by stage 3 (\(J_{13}J_{32}\)) and the determinant of the submatrix with only the dynamics of stage 4 (\(J_{44}\)).

The signed versions of the above terms (i.e., terms multiplied by the factor \((-1)^m/|J|\)) help explain our general conditions for overcompensation in density and help explain why those conditions differ between models with and without inter-stage competition. First consider models without inter-stage competition. When there is no overcompensation in any rate, all signed terms are negative (e.g., \(-J_{21}/|J|<0\) and \(J_{11}/|J|<0\) in a two-stage model). Consequently, increased mortality of any stage causes a decrease in the density of all stages. In contrast, if intra-stage competition in stage j causes sufficiently strong overcompensation in the maturation rate of stage j, then \(J_{j+1,j}\) and \(J_{jj}\) change sign. Similarly, if intra-stage competition in stage n causes sufficiently strong overcompensation in the reproductive rate of stage n, then \(J_{1n}\) changes sign. This causes some of the signed terms to change from negative to positive (e.g., overcompensation in the maturation rate of stage 1 causes \(-J_{21}/|J|>0\) and \(J_{11}/|J|>0\) in a two-stage model), which allows for the possibility of increased mortality of stage j causing an increase in density of stage i.

For models with inter-stage competition, the equations defining the responses to increased density involve signed terms that are negative and positive. For example, in a three-stage model where inter-stage competition is weak and there is no overcompensation in any rate, the sign of \(\partial N_1^*/\partial m_2\) is determined by \(-J_{12}J_{33}/|J|+J_{13}J_{32}/|J|\), whose first and second terms are positive and negative, respectively. In these systems with inter-stage competition, overcompensation in density arises either because (i) intra-stage competition is strong enough to cause a signed term to change from negative to positive or (ii) inter-stage competition is strong enough to either cause a signed term that is positive to increase in magnitude or cause signed term to change from negative to positive. As an example of the former, overcompensation in the reproduction rate of stage 3 (\(J_{13}<0\)) or overcompensation in the maturation rate of stage 2 (\(J_{32}<0\)) can cause the signed indirect effect \(J_{13}J_{32}/|J|\) from above to change from negative to positive. As an example of the latter, if the competitive effect of stage 2 on the reproduction rate of stage 3 is much stronger than the competitive effect of stage 2 on the maturation rate of stage 1, then \(J_{12}\) will be negative and large in magnitude, which causes the signed direct effect \(-J_{12}J_{33}/|J|\) from above to be large in magnitude.

The relationship between overcompensation in density and overcompensation in rates

One advantage of interpreting our conditions for overcompensation in density in terms of direct and indirect effects is that it helps clarify the relationship between overcompensation in ecological rates and overcompensation in density. This helps assess whether three predictions from previous studies using density-based or biomass-based models hold for density-based single-species models with any number of stages. First, using a density-based two-stage model, Abrams (2009) found that overcompensation in the maturation rate or reproductive rate of one stage (caused by intra-stage competition) was necessary for overcompensation in density. Our results show that overcompensation in a rate is a necessary condition in the two-stage model, but not for models with more than two stages. The underlying reason is that sufficiently strong inter-stage competition produces positive signed direct effects, which can cause overcompensation in density, even in the absence of overcompensation in a rate.

Second, previous studies using biomass-based models predict that overcompensation in the maturation rate of stage j can cause overcompensation in biomass of any stage other than stage i (de Roos, Schellekens and van Kooten et al. (2007); Karatayev, Kraft and Zipkin (2015)). Our results show that this statement holds for overcompensation in density. This is because overcompensation in density in the maturation rate of stage i affects the signs of entries \(J_{ii}\) and \(J_{i+1,i}\), one of which is always present in the equation defining \(\partial N_i^*/\partial m_j\) when \(i\ne j\). Moreover, our results show that if overcompensation in density of stage i is caused by overcompensation in the maturation rate of some stage, it must be overcompensation in the maturation of a different stage. Mathematically, this is because entries \(J_{ii}\) and \(J_{i+1,i}\) are not elements of  the submatrix (\(M_{ji}\)), which determines how stage i responds to increases in mortality of stage j.

Third, one study (de Roos, Schellekens and van Kooten et al. (2007)) using a biomass-based model has argued that if intra-stage competition causes overcompensation in the maturation rate of stage i, then there cannot be stage-specific overcompensation in density of stage i in response to increases in its own mortality. The apparent contradiction in this scenario is that overcompensation in maturation rate is often interpreted to mean ‘decreased output with increased input’ and overcompensation in density with increased mortality of the same stage is often interpreted to mean ‘increased output with decreased input’. This conclusion does not hold for our density-based model. The reason is that interpretation ‘increased output with decreased input’ does not recognize that overcompensation in density of stage i in response to increases in its own mortality is determined solely by the direct and indirect effects involving the growth rates of other stages, not the growth rate of stage i. Mathematically, our results show that there is no contradiction for our density-based model because the submatrix that defines overcompensation in density of stage i in response to increases in its own mortality is independent of the Jacobian entries whose values are affected by overcompensation in the maturation rate of stage i, (i.e., \(\partial N_i^*/\partial m_i\) is defined by \(M_{ii}\), which is independent of \(J_{ii}\) and \(J_{i+1,i}\)).

However, while the mathematical conditions defining overcompensation in density of a stage in response to increases in its own mortality and overcompensation in its maturation rate are independent, they jointly affect the stability of the equilibrium a model. Because of this, there are restrictions on when a stage can simultaneously experience both overcompensation in density in response to an increase in its own mortality and overcompensation in its maturation rate at a stable equilibrium. Specifically, in the absence of inter-stage competition, if overcompensation in the maturation rate of stage i causes stage i to experience positive density dependence (\(J_{ii}>0\)), then it is not possible for increased mortality of stage i to cause overcompensation in its biomass at a stable equilibrium. This is because in the absence of inter-stage competition, positive density dependence of stage i and overcompensation in density in response to increases in its own mortality imply the equilibrium is unstable; see Online Resource S3.2 for details. However, sufficiently strong inter-stage competition can stabilize the equilibrium and allow stage i to experience both types of overcompensation and positive density dependence at a stable equilibrium.

We point out two specific scenarios where a single stage can simultaneously experience overcompensation in density in response to increases in its own mortality rate and overcompensation in its maturation rate; numerical examples are provided in Online Resource S3.2. First, in the absence of inter-stage competition, stage 1 can experience both types of overcompensation if the overcompensation in maturation rate of stage 1 is sufficiently weak such that stage 1 experiences negative density dependence (\(J_{11}<0\)) and stage n experiences nonlinear mortality such that \(J_{nn}>0\). For example, consider a two-stage model with nonlinear adult mortality and Jacobian \(J=\left( \begin{array}{cc} -1 &{} 0.5\\ -1.5 &{} 0.05 \end{array}\right)\). This model satisfies the necessary and sufficient condition for overcompensation in density of stage 1 in response to increases in its own mortality (\(J_{22}>0\)), is stable because \(|J|>0\) and \(J_{11}+J_{22}<0\), and has overcompensation in the maturation rate of stage 1 (necessary for \(J_{21}<0\)). Second, both types of overcompensation can occur for any stage \(i<n\) if there is (i) sufficiently weak overcompensation in the maturation rate of stage i such that stage i experiences negative density dependence (\(J_{ii}<0\)), (ii) sufficiently strong overcompensation in the maturation rate of stage \(j\ne i\) such that \(\partial N_i^*/\partial m_i>0\), and (iii) sufficiently strong inter-stage competition. In this case, overcompensation in density of stage i is caused by overcompensation in the maturation rate of state j and inter-stage competition stabilizes the equilibrium.

Hydra Effects

A hydra effect occurs at a stable equilibrium when the total equilibrium density (\(N^* = \sum _i N_i^*\)) increases in response to increased stage-specific mortality, i.e., \(\frac{\partial N^*}{\partial m_i} >0\). One way to compute the derivative is to add up the responses of all stages, \(\frac{\partial N^*}{\partial m_i}= \sum _j \frac{\partial N_j^*}{\partial m_i}\). Instead, we rewrite model (1) in terms of the dynamics of the total density (N) and the densities of each class except for the class experiencing increased mortality (i.e., \(N_j\) for all \(j\ne i\)). The derivative is then computed using the same approach as above. Additional details are given in Online Resources S1.2, S2.2 and S3.3.

Below we present a summary of our results. The results largely mirror the conditions for overcompensation in density. This is expected because a necessary condition for a hydra effects is that at least one stage experiences overcompensation in density.

Hydra Effects in two-stage models

In the two-stage model, the responses to increased mortality in one stage are

$$\begin{aligned} \frac{\partial N^*}{\partial m_1}= & {} \frac{N_1}{|J|}\left[ N_1\left( \frac{\partial g_1}{\partial N_2}-\frac{\partial g_1}{\partial N_1}\right) - g_1 -m_2\right]\Biggr|_\rho \end{aligned}$$
(11)
$$\begin{aligned} \frac{\partial N^*}{\partial m_2}= & {} \frac{N_2}{|J|}\left[ N_2\left( \frac{\partial b}{\partial N_1}-\frac{\partial b}{\partial N_2}\right) + N_1\left( \frac{\partial g_1}{\partial N_2}-\frac{\partial g_1}{\partial N_1}\right) -b-g_1-m_1\right]\Biggr|_\rho \end{aligned}$$
(12)

where \(|J|>0\). For both responses, a hydra effect occurs only if there is one stage where (i) intra-stage competition that is strong enough to cause overcompensation in its maturation or reproduction rate and (ii) the effects of intra-stage competition on the per capita maturation or reproduction rate of that stage are greater than the effects of inter-stage competition. As a specific example, equation (11) is positive only if there is overcompensation in the maturation rate of stage 1 (\(N_1\partial g_1/\partial N_1+g_1<0\)) and the effects of intra-stage competition on the per capita maturation rate of stage 1 are greater (i.e., negative and larger in magnitude) than the effects of inter-stage competition (\(\frac{\partial g_1}{\partial N_2}-\frac{\partial g_1}{\partial N_1}>0\)). Equation (12) has the same interpretation, with the only difference being that a hydra effect can be driven by sufficiently strong intra-stage competition in either stage.

Hydra Effects in three-stage models

In the three-stage model, hydra effects can arise via two mechanisms. The first is that there is one stage where (i) intra-stage competition that is strong enough to cause overcompensation in its maturation or reproduction rate and (ii) the effects of intra-stage competition on the per capita maturation or reproduction rate of that stage are greater than the effects of inter-stage competition. This mechanism is the same as the two-stage model. The second mechanism is that inter-stage competition is sufficiently stronger than intra-stage competition. In numerical simulations, hydra effects at a stable equilibria were much less likely to be caused by the second mechanism. This suggests that hydra effects are more likely to be driven by strong intra-stage competition than strong inter-stage competition in natural systems.

To show how these conditions arise in the mathematical formulas, we use the specific case of the response to increased mortality in stage 1; responses to increased mortality in other stages have a similar structure and are given in Online Resource S2.2. The response to increased mortality in stage one is

$$\begin{aligned} \frac{\partial N^*}{\partial m_1} = \frac{N_1}{|J|}\biggr [&\overbrace{N_2\frac{\partial g_2}{\partial N_3}\left( N_1\frac{\partial g_1}{\partial N_2}-g_1 -N_1\frac{\partial g_1}{\partial N_1}\right) + N_1\frac{\partial g_1}{\partial N_3}\left( N_2\frac{\partial g_2}{\partial N_1}-g_2 -N_2\frac{\partial g_2}{\partial N_1}\right) }^{\text {stronger intra-stage competition promotes hydra effects}}\nonumber \\&+\overbrace{m_2\left( g_1 +N_1\frac{\partial g_1}{\partial N_1}-N_1\frac{\partial g_1}{\partial N_2}\right) +m_3\left( g_2 +N_2\frac{\partial g_2}{\partial N_2}-N_2\frac{\partial g_2}{\partial N_1}\right) }^{\text {stronger intra-stage competition promotes hydra effects}} -N_2\frac{\partial g_2}{\partial N_3}m_2 + m_2m_3\nonumber \\&\overbrace{\left( g_1 +N_1\frac{\partial g_1}{\partial N_1}\right) \left( g_2+N_2\frac{\partial g_2}{\partial N_2}\right) -N_1N_2\frac{\partial g_1}{\partial N_2}\frac{\partial g_2}{\partial N_1}+N_2\frac{\partial g_2}{\partial N_1}m_2}^{\text {stronger inter-stage competition promotes hydra effects}}\biggr ]\Biggr|_\rho. \end{aligned}$$
(13)

where \(|J|<0\). Lines 1 and 2 of equation (13) show that sufficiently strong intra-stage competition can cause a hydra effect. For this to occur, intra-stage competition must be strong enough to cause overcompensation in the maturation rate of one stage (e.g., \(g_1 +N_1\frac{\partial g_1}{\partial N_1}<0\) for the first set of terms in parentheses on line 1) and the per capita effects of intra-state competition on the maturation rate must be stronger than the per capita effects of inter-stage competition (e.g., \(\frac{\partial g_1}{\partial N_2} - \frac{\partial g_1}{\partial N_1}>0\)) in the set of terms). Line 3 shows that sufficiently strong inter-stage competition can cause a hydra effect. For this to occur, the effects of inter-stage competition (\(N_1N_2\frac{\partial g_1}{\partial N_2}\frac{\partial g_2}{\partial N_1}\)) must be sufficiently larger in magnitude than the effects of intra-stage competition (two sets of terms in parentheses on line 3).

Hydra Effects in n-stage models

The responses to increased mortality in the n-stage model when there is no inter-stage competition are given in Online Resource S3.2. The key takeaway from those equations is that sufficiently strong intra-stage competition in any stage can cause a hydra effect so long as the intra-stage competition causes overcompensation in the maturation or reproductive rate of at least one stage. In addition, our results about overcompensation in density suggest that a hydra effect is most likely to arise when there is sufficiently strong overcompensation in the maturation or reproductive rate of a single stage. This is because that scenario results in all but one stage increases in density in response to increased mortality.

The equations defining the responses to increased mortality when inter-stage competition is present are analytically intractable. We expect that the results from the three-stage model generalize to the n-stage model because the results about overcompensation in density for the three-stage model generalize to the n-stage model.

Discussion

In this study, we used an n-stage single-species model to examine how stage-structured species respond to increased mortality. We focused on identifying when increased mortality of a single stage caused an increase in the (numerical) density of one or more stages (stage-specific overcompensation in density) or an increase in total density of the population (a hydra effect). Understanding these phenomena is important because they affect conservation and population management decisions. In particular, many population management decisions may be designed under the assumption that increased removal or mortality implies reduced density of all stages, but stage-specific overcompensation in density and hydra effects do not align with this assumption. This can lead to unintended outcomes, e.g., increased removal of an invasive species may actually cause an increase in the density of the invasive species (Zipkin, Sullivan and Cooch et al. (2008)). Our results increase our understanding of the biological mechanisms that can cause overcompensation in density and hydra effects and point to future work on related phenomena.

Previous studies on single-species systems (de Roos, Persson and Thieme (2003); Abrams (2009)) have shown that overcompensation in density and hydra effects can be driven by intra-stage competition that is strong enough to cause overcompensation in the maturation or reproductive rate of one or more stages. Our study adds to this in three ways. First, our results show that sufficiently strong intra-stage competition mechanism can drive both phenomena in models with any number of stages (left column of figure 2). Second, our results show that inter-stage competition inhibits this mechanism. Specifically, the amount of intra-stage competition in stage k needed to cause overcompensation in density of stage i increases if stage k has strong inter-stage competitive effects on its own input rate or the output rate of stage \(k+1\). Third, we show that in models with three or more stages, overcompensation in density can also be caused by sufficiently strong inter-stage competition between stages (right column of figure 2). Thus, our work has helped reveal that inter-stage competition can inhibit and promote different mechanisms driving overcompensation in density and hydra effects.

The introduction lists empirical studies where overcompensation in density and hydra effects have been observed in stage-structured populations. Because hydra effects necessarily require overcompensation in density in at least one stage, it is unsurprising that hydra effects are present only in a subset of the systems where overcompensation in density occurs. In particular for the single-species systems, overcompensation in density was observed in four systems (Watt (1955); Slobodkin and Richman (1956); Nicholson (1957); Cameron and Benton (2004)) and only two also exhibited a hydra effect (compare 66% and 75% removal treatments in figure 5 of Slobodkin and Richman (1956); compare 0.3 removal treatment to other treatments in figure 6 of Watt (1955)). Unfortunately, we cannot determine if the responses in those four single-species studies were driven by overcompensation in an ecological rate or inter-stage competition because none of the studies measured how maturation or reproduction rates depend on density. However, two other studies (Buckley, Hinz and Matthies et al. (2001); Pardini, Drake and Chase et al. (2009)) provide some evidence of a causal connection between overcompensation in an ecological rate and stage-specific overcompensation in density. Both studies observed overcompensation in the survival rate to flowering and fecundity of a plant. When that was incorporated into a mechanistic model, overcompensation in density of one stage was predicted with increased mortality early in life (Buckley, Hinz and Matthies et al. (2001); Pardini, Drake and Chase et al. (2009)).

The two mechanisms driving overcompensation in density (sufficiently strong intra-stage or inter-stage competition) can both be interpreted in terms of signed direct and indirect effects. One advantage of this is that it can help connect results from previous studies on overcompensation in density in resource-explicit models. For example, de Roos (2018) and Schreiber and Rudolf (2008) explored the conditions for overcompensation in consumer density in consumer–resource systems. As shown in Online Resources S1.1 and S1.2, the conditions for overcompensation in consumer biomass in their studies are mathematically equivalent to the conditions for overcompensation in density in our two-stage model. Thus, signed direct and indirect effects also explain how stage-specific overcompensation in density arose in their consumer–resource models.

Another advantage of interpreting our conditions in terms of signed direct and indirect effects is that it helps clarify the causal relationship between overcompensation in a rate and overcompensation in density. First, overcompensation in a rate is a necessary condition for overcompensation in density only in models without inter-stage competition. This explains why previous studies (de Roos, Persson and Thieme (2003); Abrams (2009)) using models without inter-stage competition predicted that overcompensation in a rate was necessary for overcompensation in density. Second, overcompensation in density of stage i is not affected by the presence or absence of overcompensation in the maturation or reproductive rate of that stage. Thus, when overcompensation in an ecological rate causes overcompensation in density of a particular stage, the maturation or reproductive rate must be for a different stage than the stage that is the experiencing overcompensation in density. Third, overcompensation in the maturation rate of stage i does not necessarily preclude the possibility of overcompensation in density of stage i in response to increases in its own mortality. Our work in Online Resource S3.1 shows that a single stage cannot simultaneously experience both types of overcompensation at a stable equilibrium if there is no inter-stage competition and the overcompensation in maturation rate is sufficiently large to result in positive density dependence of that stage (i.e., \(J_{ii} > 0\)). However, if the stage is experiencing negative density dependence (\(J_{ii}<0\)) or inter-stage competition is sufficiently strong, then a stage can simultaneously experience both types of overcompensation at a stable equilibrium. This contrasts with biomass-based models that predict a single stage cannot simultaneously experience overcompensation in biomass (i.e., increased biomass of a stage in response to increased mortality of some stage) and overcompensation in its maturation rate (de Roos, Schellekens and van Kooten et al. (2007)).

This difference in predictions points toward the need for theory that identifies connections between the mechanisms driving overcompensation in biomass, overcompensation in density,  and hydra effects. There are empirical examples of all phenomena occurring simultaneously (Watt (1955); Slobodkin and Richman (1956); Smith et al. (1996); Meyer, Lamansky and Schill (2006); Zipkin, Sullivan and Cooch et al. (2008)) and examples where only some of the phenomena occur simultaneously (e.g., Buckley, Hinz and Matthies et al. 2001; Weidel, Josephson and Kraft 2007); see Schröder, van Leeuwen, and Cameron (2014) for a comparison of systems exhibiting overcompensation in biomass and hydra effects. The partial overlap is expected: the phenomena are not independent because changes in density and changes in biomass are not independent. This suggests that there may be similarities and differences between the mechanisms driving the three phenomena. Current theory is limited in its ability to make this comparison because biomass-based models differ from density-based models in that biomass-based models account for increases and decreases in biomass due to somatic growth. In mechanistic biomass-based models (de Roos, Schellekens and van Kooten et al. (2007); de Roos and Persson (2013); Persson and de Roos (2013)), this results in the maturation rate of state i depending on the mortality rate of stage i, which means the equation defining the response to increased mortality is similar, but not identical, to equation (3). An ideal comparison of the mechanisms driving the different phenomena would involve models that describe the changes the size distribution of a species (e.g., De Roos and Persson 2002). Nonetheless, comparing the predictions from structurally different biomass-based and density-based models may still be useful. For example, our results that a single stage can experience simultaneous overcompensation in its maturation rate and overcompensation in density in density-based models suggests that, contrary to previous predictions (de Roos, Schellekens and van Kooten et al. (2007)), it may be possible in biomass-based models for a single stage to experience simultaneous overcompensation in its maturation rate and overcompensation in biomass.

Additional theory is also needed to identify what mechanisms can drive hydra effects, overcompensation in density and overcompensation in biomass in multi-species models with stage-structured populations. Much of the work on overcompensation in biomass has focused on single-species consumer–resource models. Consequently, it is still unclear whether interactions with other species (e.g., competitors, predators or parasites) can drive overcompensation in biomass via other mechanisms. Hydra effects can arise in multi-species systems through a variety of mechanisms: subsystem instability driven by inter-specific species interactions (Cortez and Abrams (2016); Cortez (2016)), prudent exploitation by predators (Abrams (2009)), changes in cycle amplitude in systems undergoing oscillations (Abrams, Brassil, and Holt (2003); Abrams (2009); Sieber and Hilker (2012)), and adaptation of one or more species (Abrams (2009); Abrams and Vos (2003); Abrams and Matsuda (2005); Abrams (2019); Cortez and Yamamichi (2019)). There is some overlap between these mechanisms and the mechanisms found in this study. For example, subsystem instability is the mechanism causing overcompensation in density of stage i in response to increases in its own mortality (Cortez and Abrams (2016)). It is reasonable to assume that the other mechanisms driving hydra effects may also affect the possibility and likelihood of overcompensation in density in multi-species systems. This in turn suggests that those mechanisms may affect overcompensation in biomass, but it is unclear how. Thus, additional work on multi-species systems is needed to further understand the mechanisms driving these counterintuitive responses to increased mortality.