1 Introduction

Velocity boundary layer and thermal boundary layer (VBL and TBL respectively) develop on a heated flat plate due to natural convection and heat diffusion normal to the heated surface [1]. The motion of electrically-conducting liquid induces a current in the liquid, \(\overrightarrow{J}\), in the presence of a transverse magnetic field, \(\overrightarrow{B},\) and that current produces an opposing Lorentz force, (\(\overrightarrow{J}\times \overrightarrow{B})\) [2,3,4]. The Lorentz force competes with buoyancy rise and affects the growth of the velocity as well as thermal boundary layers [2]. Several engineering appliances require control of the flow and heat transfer, and hence there is a need to develop a fundamental understanding of the phenomenon of magneto-convection (convection influenced by magnetic field). Some of the important application areas include vacuum arc re-melting [4, 5], arc welding, electromagnetic braking and stirring in continuous casting of steel [4,5,6], flow in liquid metal batteries, etc. [7, 8]. Of particular interest are the cases where the magnetic effects compete with buoyancy effects. Ultrasound Doppler Velocimetry (UDV) has recently been used in some of these applications such as for velocity measurement in liquid metal electrodes [8].

Several theoretical and numerical studies are reported in the literature to predict the thermal boundary layer, velocity boundary layer, and heat transfer rate in the context of magneto-convection. These studies predict that under the effect of an applied magnetic field, the velocity and thermal boundary layers get stretched, the maximum core velocity reduces and the net heat transfer decreases from the heated surface [9,10,11]. At a higher range of Hartmann numbers (\(Ha = BL\surd (\sigma /\rho \nu )\)), when the induced magnetic field is comparable to the applied magnetic field, the frictional drag reduces, and the bulk temperature increases [11]. (Here, L is the characteristic length scale, which corresponds to the height of the plate, and \(\sigma ,\rho ,\nu\) are electrical conductivity, density, and kinematic viscosity, respectively.)

Despite several theoretical and numerical studies on magneto-convection, very few experimental studies are available for natural convection [12, 13]. To the best of our knowledge, there is no experimental observation reported for magneto-convection in the context of buoyancy-driven flows over a vertically heated flat plate. In the present study, the UDV technique is used to measure the velocity distribution in the close vicinity of the heated flat plate, and velocity profiles are drawn under varying Rayleigh as well as Hartmann numbers.

2 Experimental methodology

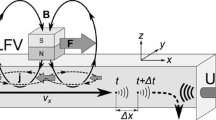
A 2 mm thick, 30 mm wide, and 80 mm high copper plate is attached to an acrylic cuboidal box 60 mm wide, 110 mm long, and 150 mm height, as shown in figure 1a. The working fluids used in our study are normal tap water and saline water with concentrations of 5% and 10% (by weight) of table salt. The Hartmann number of the working fluid changes mainly due to the changes in its electrical conductivity. With regards to the working fluids employed in the present set of experiments, the conductivity of tap water is quite small as compared to that of salt water (table 1).

Figure 1
figure 1

(a) Experimental set-up and (b) schematic representation of velocity measurement along boundary layer thickness, all the dimensions in mm.

Full size image
Table 1 Properties of working fluids at 30°C [14, 19,20,21].
Full size table

A constant wall surface temperature boundary condition is maintained by circulating thermostated (hot) water through the flat plate. The level of accuracy in velocity measurements using the UDV technique largely depends on the strength of the echo signal that the probe receives. At low flow velocities, owing to poor echo from the seeding particles, uncertainties associated with UDV-based measurements are expected to be relatively on the higher side [15]. In the experiments reported, the maximum wall temperature has been maintained at 45 °C, while maintaining the ambient temperature at 30 °C. Following this, the temperature differences between the pool and the heated plate have been taken as 5, 10, and 15 °C.

The temperature of the heated surface is measured and monitored with a k-type thermocouple coupled with a PID controller (MULTISPAN UTC 4202G, with \(\pm 1\;^\circ {\text{C}}\) accuracy and 95% confidence level). A 4 MHz UDV probe with UDOP 3010 [14] is used to measure the velocity field. Copolyamide (GRILTEX 2A P1) seeding particles 0.15% (by weight) are mixed with the working fluids. UDV probe is kept at a Doppler angle of 45° and slowly moved horizontally backward at a spatial interval of 2 mm (with \(\pm\) 0.2 mm) to capture several velocity profiles along its axis (figure 1b). To obtain the velocity profile at any given height of the plate, vertical velocity values are taken from the measured profile at several locations (2 mm apart) along the velocity boundary layer choosing the wall as a reference. The velocity profile is measured in a quasi-uniform magnetic field (a detailed explanation is given in section 3.2) near the vicinity of the heated surface, and in this experiment, we obtain such a field distribution on a straight line 30 mm above the bottom of the plate. A fixed 45° angle allows us to easily relate the horizontal movement of the UDV probe to the location of the measurement point on the horizontal velocity profile. At small Doppler angle, the UDV probe must be moved closer to the wall. Upward-moving seeding particles may collide with the probe, settle down and distort the velocity boundary layer. Uncertainty was large while fixing the wall position according to the echo profile at a high UDV angle because the echo did not have a clear peak. After trial and error, the UDV probe angle is chosen at 45° to make the measurement accurate and reliable.

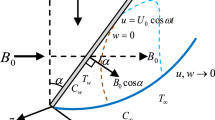
Magneto-convection is achieved by placing a \(50\times 50\times 25\) mm neodymium magnet behind the heated surface, which creates a magnetic field strength of 350 \({\text{mT}}\) on its surface. UDV measurements are taken on the mid-height of the magnet, i.e., the line where the field is horizontal (figure 6). Magnetic field strength is measured with a magnetic field meter (Metravi GM-197 AC/DC) with 4% accuracy. An average magnetic field is used to calculate the Hartmann number, and the Lorentz force per unit volume is calculated using the local velocity and the field strength at the same point. A schematic of the boundary layer with the direction of Lorentz force is shown in figure 2.

Figure 2
figure 2

(a) Schematic of natural convection-based thermal and velocity boundary layer profiles under the influence of the externally applied magnetic field. (b) Schematic representation of Lorentz force in the flow field due to the induced current.

Full size image

A comparison of UDV measurements performed in the configuration of fully developed laminar flow through a standard rectangular cross-section channel attached with a rotameter has also been carried out. The comparison resulted in a reasonably good agreement with the theoretical prediction [16, 17] as well as with the flow velocity measured by Rotameter.

2.1 Magneto-convection equations

The governing equations are the continuity, steady-state momentum and energy equations. A Lorentz force source term is included in the momentum equation (only the x-component is shown here). Induced current density is due to the flow interacting with the field (Ohm’s law), and the magnetic field is due to the permanent magnet.

$${\text{Conti}}.\quad \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(1)
$${\text{x}} - {\text{mom}}. \quad u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} + g\beta \Delta T + \left( {\frac{{\vec{J} \times \vec{B}}}{\rho }} \right)_{x}$$
(2)
$${\text{Energy}}\;{\text{eqn}}.\quad u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{J^{2} }}{{\sigma \rho C_{p} }}$$
(3)
$${\text{Ohm's}}\;{\text{law}}\quad \vec{J} = \sigma \left( {\vec{E} + \vec{v} \times \vec{B}} \right)$$
(4)
$${\text{Since applied electric field}},\quad E = 0,$$
$$\vec{J} = \sigma \left( {\vec{v} \times \vec{B}} \right)$$
(5)
$${\text{Lorentz}}\;{\text{ force}}\quad F_{L} = \left( { \vec{J} \times \vec{B}} \right)_{x} = - \sigma uB^{2}$$
(6)
$${\text{Hartmann}}\;{\text{No}}.\quad Ha = BL\surd \left( {\sigma /\rho \nu } \right)$$
(7)
$${\text{Rayleigh}}\;{\text{No}}.\quad Ra = \frac{{g\beta \Delta TL^{3} }}{\nu \alpha }$$
(8)

The magnetic field profile is mapped in the fluid domain and an exponentially-decaying profile (9) is fitted to the same. An average magnetic field (10) is then calculated and used to find the Lorentz force.

$$B (y) = 141.45{\text{exp}}(-0.036y)$$
(9)
$${B}_{avg }=\frac{{\int }_{0}^{\delta }B\left(y\right)dy}{\delta }$$
(10)

Fluid properties (with values taken from the available literatures) have the standard notation and are indicated in table 1.

3 Results and discussion

3.1 Experiments without the magnetic field

UDV measures the velocity of the flow field along its axis and gives its component along the flow based on the Doppler angle [12]. The accuracy of the measurement depends on the echo from the seeding particles; hence, a moderate flow velocity and an optimum number of particles are needed to map an accurate and smooth velocity profile inside the flow field [15,16,17].

In figure 3, the measured velocity for the flow inside the rectangular cross-sectional channel [18] is compared with the theoretical maximum velocity, and flow is measured with a standard rotameter. UDV measurement has very good agreement up to 15 LPH. At a very low flow rate, deviation occurs due to the weight of seeding particles and at a higher flow rate, deviation increases because of the transition from laminar to turbulent flow regime in the channel.

Figure 3
figure 3

Comparison of velocity measured through UDV in a rectangular cross-sectional channel with that of the theoretical approach.

Full size image

The error band is 1.162 to 10.46 mm/s, minimum at 5 LPH (1.162 mm/s) and maximum at 20 LPH (10.46 mm/s).

The raw velocity profile measured by UDV at a Doppler angle of 45° is shown in figure 4. The velocity component toward the probe is measured to be negative while the component away from it is measured as positive. The velocity boundary layer (VBL) thickness (\(\delta\)) at 30 mm height of the wall, across the line of measurement, is indicated in figure 4, evident from the sign change in the measured velocity. Temperature distribution across the heated flat plate varies in the limited range of \(\pm 1\%\) or less from bottom to top. The uncertainty in the velocity measurement by UDV is approx. \(\pm\) 0.02%. Near the stationary wall, echoes are not very clear due to multiple reflections from seeding particles. This is the inherent uncertainty in UDV measurement [15, 16]. Doppler angle is measured with an accuracy of \(\pm\) 0.5°. To draw the velocity profile along the velocity boundary layer, the average value of repeated velocity measurements at any given point is considered and shown with an error bar in figures 5, 7 and 8.

Figure 4
figure 4

Vertical velocity profile measured by UDV at Doppler angle 45°. Near 82 mm the velocity is zero on wall.

Full size image

Velocity profile inside boundary layer for normal tap water is measured for Rayleigh numbers (\(Ra\)) \(6.25\times {10}^{7}, 1.25\times {10}^{8}\mathrm{ and }1.87\times {10}^{8}\) (corresponding to ∆T of 5, 10, and 15°C, respectively) as shown in figure 5a. For all calculations, the characteristic length scale is kept fixed at L = 80 mm. With the increase in \(Ra\), the maximum velocity inside the boundary layer increases, and VBL gets stretched. Salt concentration increases the density, thermal diffusivity, thermal expansion coefficient, and viscosity of the working fluid [19,20,21]. This is evident in figure 5b—at higher concentrations, the boundary layer thickness rises due to higher heat diffusion even though ∆T is fixed at 10°C.

Figure 5
figure 5

(a) Velocity profile for tap water measured by UDV at a height of 30 mm for varying Ra. (b) VBL for different salt concentrations at a fixed \(\Delta T=10^\circ {\text{C}}\).

Full size image

3.2 Under the influence of external magnetic field

Figure 6a shows the magnetic field distribution, obtained through a 2D COMSOL simulation with a permanent magnet (of the same strength as the one used in our experiments). Note that the major field component in the fluid is horizontal.

Figure 6
figure 6

(a) Magnetic flux density distribution in x-y plane. Measurements are taken along line A-A (midpoint of magnet). (b) Variation of magnetic field along the normal to the heated surface at 30 mm height (along A-A).

Full size image

Since there is non-uniformity in the magnetic field, measurements have been taken only along line A-A (figure 6a). The Hartmann number is calculated using the average value of the magnetic field inside the velocity boundary layer (VBL). Variation of the magnetic field along the boundary layer thickness is shown in figure 6b. Magnetic field strength decreases exponentially along the boundary layer. An average value of 115 \(mT\) is calculated using equations (9) and (10), where δ is approx. 12 mm. Presence of an ambient magnetic field may cause uncertainty in the measurements, however, it is very small as the Earth’s magnetic field is ~ 50 μT. Uncertainty in the Lorentz force (\({F}_{L}=\sigma u{B}^{2})\) is due to the error in the measurement of velocity and magnetic field along velocity boundary layer, and is calculated by equation (11).

$${\epsilon }_{{F}_{L}}=\sqrt{\sum_{i=1}^{N}{\left({\epsilon }_{{x}_{i}}\frac{\partial {F}_{L}}{\partial {x}_{i}}\right)}^{2}}$$
(11)

Where \({\epsilon }_{{F}_{L}}\) is the uncertainty in Lorentz force, \({\epsilon }_{{x}_{i}}\) is the error in the individual measured component and \(\frac{\partial {F}_{L}}{\partial {x}_{i}}\) is the partial derivative of the Lorentz force with respect to the individual variable. Maximum uncertainty in the Lorentz force is approx. \(\pm\) 8% in our study.

An order of magnitude balancing of the Lorentz and buoyancy terms in the momentum equation (2), with velocity scaling as \(\sqrt{g\beta \Delta TL}\), suggests that the order of magnitude for electrical conductivity of working fluid should be,

$$\sigma \sim \frac{\rho }{{B}^{2}}\sqrt{\frac{g\beta \Delta T}{L}}$$
(12)

for stronger Joule dissipation (magnetic damping) over viscous dissipation [4]. If the electrical conductivity is small, then so is the Lorentz force as compared to the buoyancy. The effect of varying \(Ha\) at a fixed \(\Delta T\) of \(10^\circ C\) is shown in figure 7. Salt concentration in water increases the rate of heat diffusion, which results in larger buoyancy forces that compete with the Lorentz force during magneto-convection.

Figure 7
figure 7

Velocity profile with varying \(Ha\) at a fixed \(\Delta T\) of \(10^\circ C\).

Full size image

The velocity profile at 5% salt concentration and varying Rayleigh No. (6.48×107, 1.3×108 and 1.94×108) with and without magnetic field (\(Ha\) is \(0\) and \(0.75\)) is shown in figure 8. UDV measurement shows that the effect of Lorentz force is small in all the three cases as the change in Hartmann number is small.

Figure 8
figure 8

Velocity profile with 5% salt concentration with and without magnetic field at varying (a) \(Ra\) of \(6.48\times {10}^{7},(\mathbf{b}) 1.3\times {10}^{8}, (\mathbf{c}) 1.9\times {10}^{8}\).

Full size image

Though the change in maximum velocity inside the VBL is very less, a stretching of VBL is observed due to the cumulative volumetric effect of Lorentz force against buoyancy rise. Note that in these experiments, the seeding particles move along the boundary layer and sometimes penetrate through it (velocity here is generally taken to be zero in theoretical studies, which assume a very large width). It is also observed that the velocity boundary layer is thicker at low \(Ra\) as compared to moderate \(Ra\) which is also expected from theoretical considerations [1]. Once again, a larger velocity is observed at a larger Ra.

Variation of the Lorentz force inside the boundary layer at \(\Delta T\) of \(10^\circ C\) is shown in figure 9 for all the three working fluids. In the Lorentz force calculation, the magnetic field inside the boundary layer decays faster than the velocity. At 10% salt concentration, both electrical conductivity and velocity inside the boundary layer are relatively larger which results in a larger Lorentz force. Tap water has very low electrical conductivity and thus the Lorentz force is very small.

Figure 9
figure 9

Lorentz force inside boundary layer at \(\Delta T\) of \(10^\circ {\text{C}}\).

Full size image

4 Conclusions and future scope of work

In this study, using UDV we have measured the velocity profile on a fixed heated vertical plate placed in an otherwise quiescent fluid medium for varying temperature differences \((\Delta T)\) (\(5, \;10,\; 15\;^\circ {\text{C}}\)) and Hartmann numbers (\(Ha\)) (0, 0.086, 0.75 and 0.93) under quasi-static heating condition. We have demonstrated how to measure the velocity on a plane transverse to the wall by moving the UDV probe. To our knowledge, this is the first experimental study of free magneto-convection on a vertical heated wall. Higher velocity is observed at higher Ra as expected. At low \(Ra\) the velocity boundary layer thickness is more than that at higher \(Ra\). At a very low Hartmann number, the Lorentz force is relatively small as compared to the buoyancy force but still, the magnetic field stretches the velocity boundary layer.

Free ions in the flow experience the Lorentz force. An application of this is the MHD generator, where the rate of separation of ions and its effect on the open circuit voltage would affect the generator’s efficiency. Similarly, the motion of ions in a liquid metal battery (LMB) during its charging and discharging affects its voltage efficiency. The effect of a magnetic field on the natural convection of conducting liquid in a confined cavity (e.g., flows in LMB) could be explored using UDV.

In our experiments the magnetic field is non-uniform. This can affect the Lorentz force and thus also the velocity profile. In particular, it can create vorticity components that are otherwise absent with uniform magnetic field [3]. Having two magnets on the side walls, facing each other, can possibly give a uniform field that is still perpendicular to the flow direction. However, bringing two strong permanent magnets close to each other needs extreme caution and customized fixtures to hold the magnets must be designed. We plan to investigate the low Hartmann magneto convection under this arrangement.