1 Introduction

A growing number of non-linear loads in distribution system such as diode rectifiers used in adjustable speed drives, electronic ballast used in fluorescent lamps, welding equipment, arc furnaces and other types of switching loads generate harmonic currents and consequent distortion of system voltages. As a result, the power quality of the distribution system is adversely affected in terms of higher power losses and malfunction of equipment fed from the line. Power factor improvement and reduction of harmonics in the system can be achieved by means of passive filters, active filters or hybridisation of both types. The potentialities and limitations of passive filters, their performance optimisation using particle swarm optimization (PSO) algorithm and the performance improvement of distribution system have been investigated by Das [1], Na He et al [2] and Rivas et al [3]. As a means of overcoming certain limitations of the passive filter, active filters have been introduced subsequently. An active filter needs a controller to process the system signals, generate a reference current waveform and insulated gate bipolar transistor (IGBT) gate trigger signals so as to inject the compensation currents at the point of common coupling (PCC). The control algorithm can be structured based on analytical equations up to the reference current generation followed by a set of regulators for processing of current error [4,5,6]. Since the entire system is characterised by non-linearities and possible parameter variations, a set of fuzzy logic-based proportional integral (PI) controllers for compensation is advantageous instead of classical PI controllers [7,8,9,10]. Many of the active filter topologies are marked by high kVA rating, which imply higher complexity and cost. Further, the resulting high DC link voltage for effective compensation of higher-order harmonic currents demands higher voltage rating of the semiconductor switches and reliability issues [4]. These problems have motivated the development of hybrid active power filters for harmonic reduction [11, 12]. The hybrid filter topology generally consists of a shunt configuration comprising a passive and an active compensator in series. Different control algorithms and strategies have been reported by many authors with varying levels of performance regarding supply-side power factor and total harmonic distortion (THD) [13,14,15,16,17,18,19,20]. The active filters are capable of directing all the harmonic load current components to the passive filter and thereby eliminate any possibility of resonance in the supply system [13]. One relevant idea that has not garnered much attraction is related to the introduction of fuzzy logic theory-based PI controller in the hybrid compensation scheme for handling the inherently present non-linear control problems.

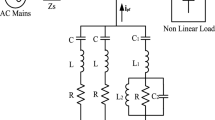
This paper deals with design and simulation of a hybrid filter for elimination of harmonics in a three-phase distribution network feeding non-linear loads. The configuration of the hybrid filter consists of selective fifth and seventh harmonic elimination passive filter connected in series with active filter and terminated with a capacitor as shown in figure 1. For controlling the active filter, a non-linear control algorithm based on synchronously rotating reference frame is utilised. This yields a reference current waveform and forces injection of harmonic currents, which are defined by a pair of fuzzy logic-based PI controllers. For sustaining the compensator action, it is necessary to regulate the DC link capacitor voltage, which is also carried out using another fuzzy logic controller.

Figure 1
figure 1

Configuration of shunt hybrid power filter.

Full size image

2 General theory of fuzzy control

In cases where the phenomena and the mathematical model are not fully understood or non-linearities are present, application of conventional feedback theory has many limitations. An alternative formulation of the control problem is by using fuzzy logic where linguistic variables are used to replace analytical terms in the mathematical model. In general, the FLC consists of three stages: fuzzification, inference with rule base and defuzzification [9], as shown in figure 2. During the fuzzification, the numerical input variables are converted into equivalent linguistic variables as fuzzy sets. Then, the input fuzzy sets are sent to the inference mechanism to obtain output fuzzy sets based on the fuzzy rule base table. Finally, the output fuzzy sets are converted into crisp variables as the output, which represents the actuating signal.

Figure 2
figure 2

Structure of the fuzzy logic controller.

Full size image

3 Power and filter circuits

Figure 1 shows a three-phase distribution circuit feeding a set of non-linear loads, which require power factor and harmonic compensation. The compensator configuration consists of a passive part made up of parallel connected 5th and 7th selective harmonic elimination branches in series with a low rating active power filter provided with a DC link capacitor, the whole compensator being wired in the form of a shunt hybrid power filter. The mathematical model of the whole circuit has been developed for formulating the non-linear control problem and is presented next.

3.1 Shunt hybrid power filter modelling

By applying Kirchhoff’s laws in figure 1, the equivalent equation governing all the three phases in generic form is obtained [10, 20] as follows:

$$ V_{sk} = L_{PFeq} \frac{{di_{fk} }}{dt} + R_{PFeq} i_{fk} + \frac{1}{{C_{PFeq} }}\int {i_{fk} } dt\mathop {}\limits_{{}} + V_{kM} + V_{MN} $$
(1)

where i fk is the filter current, k = 1, 2, 3 represent the three phases and R PFeq , L PFeq and C PFeq are equivalent parameter values of the 5th and 7th selective harmonic filters. V MN represents the voltage between the active filter and supply neutral.

The capacitor current I dc and voltage V dc are related by

$$ \frac{{dV_{dc} }}{dt} = \frac{1}{{C_{dc} }}i_{dc} $$
(2)

Assuming balanced supply voltage, we get

$$ V_{s1} + V_{s2} + V_{s3} = 0 $$

Considering Eq. (1) for k = 1, 2 and 3 and adding we get

$$ V_{MN} = - \frac{1}{3}_{{}} \sum\limits_{k = 1}^{3} {_{{}} V_{kM} } $$
(3)

The switching function \( C_{k} \)of the kth leg of the inverter [13] is defined as in (4), where \( S_{k} \)and \( S_{k}^{\prime } \) are the switches in the same leg.

$$ C_{k} = \left\{ {\begin{array}{*{20}c} {1} & {{\text{if}}\;S_{k} \;{\text{is}}\;On\;{\text{and}}\;S_{k}^{\prime } \;{\text{is}}\;Off} \\ {0} & {{\text{if}}\;S_{k} \;{\text{is}}\;Off\;{\text{and}}\;S_{k}^{\prime } \;{\text{is}}\;On} \\ \end{array} } \right. $$
(4)

Thus, with \( V_{kM} = C_{k} V_{dc} \) and differentiation of the same leads to

$$ \frac{{dV_{kM} }}{dt} = C_{k} \frac{{dV_{dc} }}{dt}. $$

By combining Eqs. (1), (3) and (4) and incorporating switching function C k , the following equations are obtained:

$$ \begin{aligned} \frac{{dV_{sk} }}{dt} =\,\, & L_{PFeq} \frac{{d^{2} i_{fk} }}{{dt^{2} }} + R_{PFeq} \frac{{di_{fk} }}{dt} + \frac{1}{{C_{PFeq} }}i_{fk} + \left( {C_{k} - \sum\limits_{m = 1}^{3} {C_{m} } } \right)\frac{{dV_{dc} }}{dt} \\ \frac{{d^{2} i_{fk} }}{{dt^{2} }} = & - \frac{{R_{PFeq} }}{{L_{PFeq} }}\frac{{di_{fk} }}{dt} - \frac{1}{{C_{PFeq} L_{PFeq} }}i_{fk} - \frac{1}{{L_{PFeq} }}\left( {C_{k} - \frac{1}{3}\sum\limits_{m = 1}^{3} {C_{m} } } \right)\frac{{dV_{dc} }}{dt} + \frac{1}{{L_{PFeq} }}\frac{{dV_{dc} }}{dt} \\ \end{aligned} $$
(5)

Defining q nk as an overall switching function, it is obtained as

$$ q_{nk} = \left( {C_{k} - \frac{1}{3}\sum\limits_{m = 1}^{3} {C_{m} } } \right)_{n} $$

where n = 0 or 1 and the value of q nk relies on the phase k and switching function. In other words, the transformation given below depends on the parameters C 1, C 2, C 3 [14, 20] and indicates the interaction among the three phases.

$$ \left[ {\begin{array}{*{20}c} {q_{n1} } \\ {q_{n2} } \\ {q_{n3} } \\ \end{array} } \right] = \frac{1}{3}\left[ {\begin{array}{*{20}c} 2 & { - 1} & { - 1} \\ { - 1} & 2 & { - 1} \\ { - 1} & { - 1} & 2 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ \end{array} } \right] $$
(6)

Re-writing Eq. (2) in terms of a switching function k and filter current i fk we get

$$ \frac{{dV_{dc} }}{dt} = \frac{1}{{C_{dc} }}\sum\limits_{k = 1}^{3} {q_{nk} i_{fk} = \frac{1}{{C_{dc} }}\left[ {q_{n123} } \right]}^{T} \left[ {i_{f123} } \right] $$
(7)

Since zero-sequence component of the filter current is absent, i f3 can be expressed by

$$ i_{f3} = \, {-} \, \left( {i_{f1} + i_{f2} } \right) $$

A similar substitution of the variable q n enables the modelling of the capacitor operation as

$$ \frac{{dV_{dc} }}{dt} = \frac{1}{{C_{dc} }}\left[ {2q_{n1} + q_{n2} } \right]_{{}} i_{f1} + \frac{1}{{C_{dc} }}\left[ {q_{n1} + 2q_{n2} } \right]_{{}} i_{f2} $$
(8)

The entire model of the shunt hybrid power filter in abc reference frame is represented by the following equations:

$$ L_{PFeq} \frac{{d^{2} i_{f1} }}{{dt^{2} }} = - R_{PFeq} \frac{{di_{f1} }}{dt} - \frac{1}{{C_{PFeq} }}i_{f1} - q_{n1} \frac{{dV_{dc} }}{dt} + \frac{{dV_{s1} }}{dt} $$
(9)
$$ L_{PFeq} \frac{{d^{2} i_{f2} }}{{dt^{2} }} = - R_{PFeq} \frac{{di_{f2} }}{dt} - \frac{1}{{C_{PFeq} }}i_{f2} - q_{n2} \frac{{dV_{dc} }}{dt} + \frac{{dV_{s2} }}{dt} $$
(10)
$$ C_{dc} \frac{{dV_{dc} }}{dt} = \left[ {2q_{n1} + q_{n2} } \right]_{{}} i_{f1} + \left[ {q_{n1} + 2q_{n2} } \right]_{{}} i_{f2} $$
(11)

3.2 Equations in d–q frame

Equations (9)–(11) describing the system model are transformed into the synchronous orthogonal frame using the transformation matrix [14]

$$ T_{dq}^{123} = \sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}c} {\cos \theta } & {\cos \left( {\theta - {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}} \right)} & {\cos \left( {\theta - {\raise0.7ex\hbox{${4\pi }$} \!\mathord{\left/ {\vphantom {{4\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}} \right)} \\ { - \sin \theta } & { - \sin \left( {\theta - {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}} \right)} & { - \sin \left( {\theta - {\raise0.7ex\hbox{${4\pi }$} \!\mathord{\left/ {\vphantom {{4\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}} \right)} \\ \end{array} } \right] $$
(12)

where \( \theta = \omega t \) and ω represents the mains frequency in rad/s.

Equation (7), after transformation, takes the following form:

$$ \begin{aligned} \frac{{dV_{dc} }}{dt} = & \frac{1}{{C_{dc} }}\left( {T_{dq}^{123} \left[ {q_{ndq} } \right]} \right)^{T} \left( {T_{dq}^{123} \left[ {i_{dq} } \right]} \right) \\ = & \frac{1}{{C_{dc} }}\left[ {q_{ndq} } \right]\left[ {i_{dq} } \right] \\ \end{aligned} $$
(13)

On the other hand, Eqs. (9) and (10) are combined and written as

$$ \frac{{d^{2} }}{{dt^{2} }}\left[ {i_{f12} } \right] = - \frac{{R_{PFeq} }}{{L_{PFeq} }}\frac{d}{dt}\left[ {i_{f12} } \right] - \frac{1}{{C_{PFeq} L_{PFeq} }}\left[ {i_{f12} } \right] - \frac{1}{{L_{PFeq} }}\left[ {q_{n12} } \right]\frac{{dV_{dc} }}{dt} + \frac{1}{{L_{PFeq} }}\frac{d}{dt}\left[ {V_{s12} } \right] $$
(14)

The aforementioned transformations when applied to Eq. (14) yields

$$ \frac{{d^{2} }}{{dt^{2} }}\left[ {T_{12}^{dq} \left[ {i_{dq} } \right]} \right] = - \frac{{R_{PFeq} }}{{L_{PFeq} }}\frac{d}{dt}\left[ {T_{12}^{dq} \left[ {i_{dq} } \right]} \right] - \frac{1}{{C_{PFeq} L_{PFeq} }}T_{12}^{dq} \left[ {i_{dq} } \right] - \frac{1}{{L_{PFeq} }}T_{12}^{dq} \left[ {q_{ndq} } \right]\frac{{dV_{dc} }}{dt} + \frac{1}{{L_{PFeq} }}\frac{d}{dt}\left[ {T_{12}^{dq} \left[ {V_{dq} } \right]} \right] $$
(15)

After simplification and reduction of Eq. (15) the following relation is obtained.

$$ \begin{aligned} T_{12}^{dq} \frac{{d^{2} }}{{dt^{2} }}\left[ {i_{dq} } \right] + \left( {\frac{d}{dt}T_{12}^{dq} } \right)\frac{d}{dt}\left[ {i_{dq} } \right] + \left( {\frac{d}{dt}T_{12}^{dq} } \right)\frac{d}{dt}\left[ {i_{dq} } \right] + \left( {\frac{{d^{2} }}{{dt^{2} }}\left[ {T_{12}^{dq} } \right]} \right)\left[ {i_{dq} } \right] \hfill \\ = - \frac{{R_{PFeq} }}{{L_{PFeq} }}\frac{d}{dt}\left[ {T_{12}^{dq} \left[ {i_{dq} } \right]} \right] - \frac{1}{{C_{PFeq} L_{PFeq} }}T_{12}^{dq} \left[ {i_{dq} } \right] - \frac{1}{{L_{PFeq} }}T_{12}^{dq} \left[ {q_{ndq} } \right]\frac{{dV_{dc} }}{dt} + \frac{1}{{L_{PFeq} }}\frac{d}{dt}\left[ {T_{12}^{dq} \left[ {V_{dq} } \right]} \right] \hfill \\ \end{aligned} $$
(16)

Further simplification of (16) leads to the following equation in d–q frame of reference.

$$ \begin{aligned} \frac{{d^{2} }}{{dt^{2} }}\left[ {i_{dq} } \right] = - \left[ {\begin{array}{*{20}c} {\frac{{R_{PFeq} }}{{L_{PFeq} }}} & { - 2\omega } \\ {2\omega } & {\frac{{R_{PFeq} }}{{L_{PFeq} }}} \\ \end{array} } \right]\frac{d}{dt}\left[ {i_{dq} } \right] - \left[ {\begin{array}{*{20}c} { - \omega^{2} + \frac{1}{{C_{PFeq} L_{PFeq} }}} & { - \omega \frac{{R_{PFeq} }}{{L_{PFeq} }}} \\ {\omega \frac{{R_{PFeq} }}{{L_{PFeq} }}} & { - \omega^{2} + \frac{1}{{C_{PFeq} L_{PFeq} }}} \\ \end{array} } \right]\left[ {i_{dq} } \right] - \frac{1}{{L_{PFeq} }}\left[ {q_{ndq} } \right]\frac{{dV_{dc} }}{dt} + \frac{1}{{L_{PFeq} }}\frac{d}{dt}\left[ {V_{dq} } \right] \\ + \frac{1}{{L_{PFeq} }}\left[ {\begin{array}{*{20}c} 0 & { - \omega } \\ \omega & 0 \\ \end{array} } \right]\left[ {V_{dq} } \right] \\ \end{aligned} $$
(17)

The complete d–q frame dynamic model of the system is obtained from Eqs. (13) and (17) and takes the following form:

$$ L_{PFeq} \frac{{d^{2} i_{d} }}{{dt^{2} }} = - R_{PFeq} \frac{{di_{d} }}{dt} + 2\omega L_{PFeq} \frac{{di_{q} }}{dt} - \left( { - \omega^{2} L_{PFeq} + \frac{1}{{C_{PFeq} }}} \right)i_{d} + \omega R_{PFeq} i_{q} - q_{nd} \frac{{dV_{dc} }}{dt} + \frac{{dV_{d} }}{dt} - \omega V_{q} $$
(18)
$$ L_{PFeq} \frac{{d^{2} i_{q} }}{{dt^{2} }} = - R_{PFeq} \frac{{di_{q} }}{dt} - 2\omega L_{PFeq} \frac{{di_{d} }}{dt} - \left( { - \omega^{2} L_{PFeq} + \frac{1}{{C_{PFeq} }}} \right)i_{q} - \omega R_{PFeq} i_{d} - q_{nq} \frac{{dV_{dc} }}{dt} + \frac{{dV_{q} }}{dt} + \omega V_{d} $$
(19)
$$ C_{dc} \frac{{dV_{dc} }}{dt} = q_{nd} i_{d} + q_{nq} i_{q} $$
(20)

3.3 Control of harmonic currents

Based on the load and compensator models presented in sections 3.1 and 3.2, the control problem is formulated with the objective of minimising supply-side harmonic currents and improving the power factor. In addition, for maintaining the performance during load fluctuations it is also necessary to maintain a desired voltage across the DC link capacitor. The control law is derived using the following approach.

Re-arranging Eqs. (18) and (19), the control variables u d and u q are written as

$$ u_{d} = 2\omega L_{PFeq} \frac{{di_{q} }}{dt} + \omega R_{PFeq} i_{q} - q_{nd} \frac{{dV_{dc} }}{dt} + \frac{{dV_{d} }}{dt} - \omega V_{q} $$
(21)
$$ u_{q} = - 2\omega L_{PFeq} \frac{{di_{d} }}{dt} - \omega R_{PFeq} i_{d} - q_{nq} \frac{{dV_{dc} }}{dt} + \frac{{dV_{q} }}{dt} + \omega V_{d} $$
(22)

Processing the current harmonics in terms of the decoupled i d –i q components and generating the respective errors along with their derivatives, the required inputs to the fuzzy logic controller are obtained. The idea is to dynamically update the PI controller parameters by the process of fuzzification, inference mechanism and defuzzification. The pair of equations relating the control variables u d and u q with d–q axis variables i d and i q now take the following form:

$$ u_{d} = L_{PFeq} \frac{{d^{2} i_{d} }}{{dt^{2} }} + R_{PFeq} \frac{{di_{d} }}{dt} + \left( { - \omega^{2} L_{PFeq} + \frac{1}{{C_{PFeq} }}} \right)i_{d} $$
(23)
$$ u_{q} = L_{PFeq} \frac{{d^{2} i_{q} }}{{dt^{2} }} + R_{PFeq} \frac{{di_{q} }}{dt} + \left( { - \omega^{2} L_{PFeq} + \frac{1}{{C_{PFeq} }}} \right)i_{q} $$
(24)

By taking the Laplace Transform of (23) and (24), the transfer function is obtained.

$$ \frac{{I_{d} (s)}}{{U_{d} (s)}} = \frac{{I_{q} (s)}}{{U_{q} (s)}} = \frac{1}{{L_{PFeq} \left( {s^{2} + \frac{{R_{PFeq} }}{{L_{PFeq} }}s + \frac{1}{{C_{PFeq} L_{PFeq} }} - \omega^{2} } \right)}} $$
(25)

Re-arranging Eqs. (21) and (22) for expressing the variables q nd and q nq in terms of the other system variables, the following two equations are obtained:

$$ q_{nd} = \frac{{2\omega L_{PFeq} \frac{{di_{q} }}{dt} + \omega R_{PFeq} i_{q} + \frac{{dV_{d} }}{dt} - \omega V_{q} - u_{d} }}{{\frac{{dV_{dc} }}{dt}}} $$
(26)
$$ q_{nq} = \frac{{ - 2\omega L_{PFeq} \frac{{di_{d} }}{dt} + \omega R_{PFeq} i_{d} + \frac{{dV_{q} }}{dt} - \omega V_{d} - u_{q} }}{{\frac{{dV_{dc} }}{dt}}} $$
(27)

Equations (26) and (27) are interpreted as defining control laws for compensation.

3.4 DC link voltage control

In a hybrid compensation technique, switching loss in active power filter is directly proportional to the DC link voltage, and regulation of this voltage is required for effective operation [13, 20, 21]. An additional fuzzy logic-based PI controller is used to regulate the DC link capacitor voltage. The electrical quantity adjusted by this designed voltage regulator is \( i_{q1}^{*} \).

Focusing on the reactive component \( i_{q} \)for charging the link capacitor, the governing Eq. (20) takes the following form:

$$ C_{dc} \frac{{dV_{dc} }}{dt} = q_{nq} i_{q} $$
(28)

Defining the input equivalent voltage as

$$ u_{dc} = \, q_{nq} i_{q.} $$

The active filter reactive current is given by

$$ i_{q} = \frac{{u_{dc} }}{{q_{nq} }} = \frac{{u_{dc} V_{dc} }}{{q_{nq} V_{dc} }} $$
(29)

Under normal operating conditions of active filter, the voltage \( V_{Mq} \) called q axes voltage of the active filter takes the form \( V_{Mq} \cong q_{nq} V_{dc} \) [20].

$$ V_{Mq} = - Z_{PFeq1} i_{q1}^{*} $$
(30)

where \( Z_{PFeq1} \)is the equivalent impedance of the passive filter for fundamental frequency and its DC component is \( i_{q1}^{*} \)

Now the DC loop control law is deduced from (29) and (30) as

$$ i_{q1}^{*} = \frac{{V_{dc} }}{{ - Z_{PFeq1} i_{q} }}u_{dc} $$
(31)

The filter current in three phases are expressed as [13]

$$ \left[ {\begin{array}{*{20}c} {i_{f1} } \\ {i_{f2} } \\ {i_{f3} } \\ \end{array} } \right] = \sqrt {\frac{2}{3}} i_{q} \left[ {\begin{array}{*{20}c} { - \sin \theta } \\ { - \sin \left( {\theta - {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}} \right)} \\ { - \sin \left( {\theta - {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}} \right)} \\ \end{array} } \right] $$
(32)

The rms value of the fundamental component of the filter current i f is given by

$$ i_{f} = \frac{{i_{q} }}{\sqrt 3 } $$
(33)

Substitution of Eq. (33) into (31) yields the Laplace transformed control law as

$$ I_{q1}^{*} (s) = \frac{{V_{dc} (s)}}{{\sqrt 3 Z_{PFeq1} I_{f} (s)}}U_{dc} (s) $$
(34)

To keep the DC link voltage close to the reference value, the error voltage \( \tilde{V}_{dc} = V_{dc}^{*} - V_{dc} \) is processed by a fuzzy logic controller. The aforementioned power circuit along with the compensator has to be interfaced with an appropriate controller for generating gate trigger waveforms for the IGBTs of the active filter. This will minimise the harmonic currents drawn from the mains and also for sustaining the DC link voltage across capacitor through a regulator action. In view of inherent non-linearities present in the system and the possibility of fluctuation of source voltage and/or loading pattern, a heuristic controller based on fuzzy logic theory is appropriate.

4 Development of fuzzy logic controller

Essentially, the control action has to be incorporated in the d–q axes current loops and the capacitor voltage regulator loop. The requirement of injecting compensating harmonic currents has to be implemented by separating the load side harmonic currents in comparison with the filter current to generate three error channels, one each for I d , I q and V dc as shown in figure 3. Accordingly, there are three channels of control action for handling a corresponding three numbers of error signals and their derivatives. Considering the error and its rate of change as fuzzy variables, their processing is carried out using fuzzy logic controller in order to dynamically vary the K P and K I parameters [8].

Figure 3
figure 3

Configuration of fuzzy controller.

Full size image

Figure 4 shows the structure of the control scheme, which consists of blocks for d–q axes transformation, reference current generation using non-linear control law along with the elements of fuzzy-based PI control scheme. Essentially, this scheme generates a set of IGBT gate trigger signals for 6 pulse voltage-fed inverter for realising the compensator action in the power circuit.

Figure 4
figure 4

Architecture of the control scheme for shunt hybrid power filter.

Full size image

4.1 Fuzzy logic-based control of active filter

The aim is to obtain harmonics-free source currents which are in phase with the supply voltages. The approach is to replace the conventional PI controllers by fuzzy logic-based PI controllers. The implementation of FLC is characterised by utilising error (e) and its derivative (∆e). The fuzzy logic controller is characterised by choice of five linguistic variables for input and output quantities, Gaussian membership function and ‘centroid’-based defuzzification. Defining the error (e) between the reference harmonic current (i ref ) and injected filter current (i f ), leads to the formulation of fuzzy rules, which are based on error, its sign and rate of change of the same. The choice of linguistic description of the output of the fuzzy controller is summarised in table 1 and is applicable to d and q axes current control channels.

Table 1 Fuzzy rule base for current control loop.
Full size table

4.2 DC capacitor voltage control

Based on the DC voltage error and its rate of change with time, the fuzzy control algorithm is implemented to regulate the capacitor voltage. The objective is to improve the dynamic performance of the hybrid filter under variable load conditions. A Gaussian membership function is suitable for this application. The rule table contains 49 rules as shown in table 2.

Table 2 Fuzzy set rules for voltage control loop.
Full size table

5 Simulation results

The simulation schematic covering the entire supply side at 400 V, 50 Hz and load parameters along with the elements of shunt hybrid filter has been created using power system block set of Matlab/Simulink. Here, by considering various loads as given below, the performance of the compensator is evaluated:

  1. 1.

    Current source type non-linear load

  2. 2.

    Voltage source type non-linear load

  3. 3.

    Dynamic load variation

  4. 4.

    Unbalanced load.

The aforementioned parameters are summarised in table 3.

Table 3 Specification of parameters.
Full size table

5.1 Current source type non-linear load

The three-phase main supplies a diode bridge rectifier feeding an R–L load, which imposes a typical flat top non-linearity in the current waveform, resulting in pronounced harmonic at the supply side. The hybrid compensator with non-linear control algorithm using fuzzy logic-based PI controller is introduced to mitigate the above situation. The simulation results at steady state of the proposed hybrid power filter with the above load are presented in figure 5a to e covering the waveforms of three-phase source voltage (VS123), load current (IL123), source current (IS123) after compensation, filter current (IF123) and DC link voltage (Vdc). respectively.

Figure 5
figure 5

Steady-state response of shunt hybrid filter for current source type non-linear load.

Full size image

Figure 6a and b shows the harmonics spectrum of supply current before compensation and after compensation, respectively. The results indicate that the THD of the source current of phase 1 is reduced from 25.74% to 3.43% due to the introduction of the shunt hybrid filter. The shunt hybrid filter is found be effective in handling the compensation requirements of the entire set of load variations.

Figure 6
figure 6

Harmonic spectrum of source current in phase 1 (a) without filter, (b) with filter.

Full size image

5.2 Dynamically varying R–L load

It is quite common that the load currents handled by a distribution feeder vary widely over the time of the day. Hence it is desirable that the filter is able to handle dynamically varying load conditions with appropriate correction. The simulation results for dynamic change of load current from 11 A(rms) to 17.9 A at t = 2 s, are presented in figure 7a to e covering source voltage (VS123), load current (IL123), source current (IS123), filter current (IF123) and DC link voltage waveforms, respectively. Fuzzy-based controller designed for this application maintains a low level of THD at the source end along with effective regulation of the DC link voltage. Further, the indirect effect of harmonic correction for power factor improvement has also been investigated in the case of R–L load and the simulations results pertaining to the same are shown in figure 8. The results show that the source side power factor comes closer to unity under varying load conditions.

Figure 7
figure 7

Response of shunt hybrid filter for dynamic variation in current source type non-linear load.

Full size image
Figure 8
figure 8

Phase voltage and current waveforms under dynamic variation in current source type non-linear load.

Full size image

5.3 Voltage source type non-linear load

Many appliances, such as UPS and motor drives, connected to a distribution line have in-built rectifiers terminated with high-value capacitors. Such a load draws high values of spike currents of opposite polarity in every cycle of the mains and is incorporated in the simulation schematic for examining the filter performance. The simulation results corresponding to this case study is presented in figure 9a to e, which show the source voltage (VS123), load current (IL123), supply current (IS123) after compensation, filter current (IF123) and DC link voltage (Vdc) waveforms, respectively. Figure 10a and b show the harmonic spectrum of line currents from mains before and after filtering, which indicates that the THD of the source current is considerably reduced from 29.55% to 4.08%.

Figure 9
figure 9

Response of shunt hybrid filter for voltage source type non-linear load.

Full size image
Figure 10
figure 10

Harmonic spectrum of source current in phase 1 (a) without filter, (b) with filter.

Full size image

5.4 Dynamically varying R–C load

By introducing a step increase in load current to the extent of doubling the rms value of the R–C circuit, the ability of the hybrid filter to mitigate the harmonic current dynamically is examined in the simulation setup. The results of this simulation, where the load current changes from 15.95 A (rms) to 29.32 A at 2 s are shown in figure 11a to e. It is seen that the designed hybrid filter reduces the harmonic content within a THD of 5%, in addition to maintaining a steady DC link voltage.

Figure 11
figure 11

Performance of the shunt hybrid filter under varying R–C load condition.

Full size image

5.5 Unbalanced load

Distribution networks are characterised by unbalanced phase currents and it is necessary to examine the effectiveness of the designed hybrid filter for handling such loads. For simulation, this unbalance is introduced by the parallel connection of a single-phase diode rectifier fed R–L load with R = 20Ω and L = 5 mH in phase 1 only. The steady-state response of the entire system is depicted in figure12a to e. It is observed from the results that the THD of phase 1 current is 2.05% at the supply side, while the remaining phase current THDs are 4.65% and 4.60%, respectively.

Figure 12
figure 12

Performance of shunt hybrid filter in unbalanced load condition.

Full size image

6 Limitations and future scope

Although a three-phase distribution system for power quality enhancement has been considered in this paper, it is limited to a three-wire system only with isolated neutral. Hence, issues arising out of zero-sequence currents due to load unbalance have not been considered. This research work can be extended for a three-phase four-wire system. Further, incorporation of controllers utilising various other soft computing techniques such as neural, fuzzy-neural and genetic algorithms can also be carried out as further work.

7 Conclusion

The design of hybrid filter along with fuzzy logic-based PI controller is carried out by formulating the non-linear control scheme with synchronously rotating reference frame theory-based reference current generation. The overall system is simulated using power system block set of MATLAB SIMULINK software for different types of non-linear loads. The steady-state response of the proposed filter for current source type non-linear load and for a step load disturbance shows that the source current is sinusoidal after compensation and DC link voltage is also maintained constant. The Fourier analysis indicates that the THD has been reduced to 3.43%. The phase voltage and current waveform depict that the power factor is maintained around 0.9. Similar results have been obtained when the supply system feeds RC-type non-linear loads. Finally, the ability of the hybrid compensator for handling unbalanced loads with improved power quality of the distribution system is presented. Further, it is observed that in all the aforementioned load conditions, the source currents are maintained nearly sinusoidal and also in phase with the respective system voltages. Furthermore, the THD has been brought down to well within 5% as stipulated by IEEE 519-1992 standard in all the above cases. Thus, the introduction of fuzzy logic-based PI controller is capable of suppressing the harmonics present in the supply currents and improves the source side power factor. Incidentally, on account of lower DC link voltage, the rating of the active power filter used in hybrid scheme is considerably reduced.