1 Introduction

Crashworthiness is the measure of capacity of a structure and its components to protect the occupants in case of crash. It accounts vehicle’s structural ability to plastically deform and yet maintain a sufficient space for its occupant’s survival during crash. The desire to improve crashworthiness cannot be overestimated. The National Highway Traffic Safety Administration (NHTSA), USA revealed that 30,800 fatalities and over 2,362,000 injuries were reported in year 2012 due to vehicle crashes in the USA. alone whereas in India, there were 243,475 fatalities in year 2011 [1]. In Bhopal alone, road accidents data during preceding years is quite alarming and same is reproduced in table 1 for last four years [2]. It is to be noted that these accidents are results of several reasons associated with the driving. However, most of these include the crash related fatalities or injuries. Hence, more emphasis is put forward for developing vehicles with higher crashworthiness. In order to reduce such fatalities in the coming years, vehicles in India need to be designed and complied for higher crashworthiness and this requires use of innovative technology for improving the efficiency of vehicle crash tubes with minimum addition of weight to the vehicles. This can only be improved by the use of proper material and innovative design.

Table 1 Road accidents during last four years for Bhopal, MP, India [2].
Full size table

It is important to note that, most of the investigation reports had revealed the poor crashworthiness of vehicles under such accidents [3–6]. Various energy absorbers are available to improve the crashworthiness of these vehicles, without drastically increasing the weight. The components of deformable energy absorbers which improves crashworthiness include as steel drums, circular tubes, tubular rings, square tubes, corrugated tubes, multi-corner columns, frusta, struts, honeycomb cells, sandwich plates and some other special shapes such as stepped circular thin-walled tubes and top-hat thin-walled sections [7–9]. In such situations, progressive folding collapse of thin-walled structures is an efficient energy absorber because it can undergo large displacement at near constant stress. Moreover, it is also economical and easy to manufacture [10]. Tube sections are widely used as energy absorbers in civil, mechanical, marine and aeronautical applications [11]. In modern automotive design thin-walled columns have been used in the design of crash boxes and bumper beams while for rail vehicles, upfront had been used to reduce the crippling impact load [12, 13]. Further, to reduce severe neck and spinal injuries in case of air crash, seats had been redesigned by placing two aluminium tubes over the seat rails and between two seat brackets in the aircraft industry [14, 15]. Although these retrofitted seats were 3% heavier than the original design, but these helped to decrease the acceleration experienced by the dummy occupant by 50% during a vertical drop test. Thin-walled sections could also be installed at the foot of elevator shaft as an energy dissipating shock absorber [16]. For crashworthiness applications recently developed metallic foams play a great role, as they showed ability to undergo large plastic deformation at a relatively constant load level [17–20]. It has been found that by filling thin-walled sections with foam, the energy absorption capacity can be improved significantly. The increase is mainly accredited to the interaction between the foam filler and the tube wall. Hence, investigation of their deformation behaviour under different loading scenarios and development of alternative lightweight designs is the need of current research.

In the present paper, different types of energy absorbers along with their deformation modes are summarized in section titled ‘Energy absorbers’. Under ‘Concepts of collapse load and energy absorption’ section, simple expression to compute the peak load, stroke efficiency and energy efficiency is discussed. Wherein, ‘Crashworthiness by plastic collapse’ section deals with the plastic hinge formation and fold development mechanism, symmetric mode, extensional mode, asymmetric mixed modes. In the next section, brief of metallic foams and their use in crashworthiness over polymeric foams is discussed. In ‘Foam-filled tubes’ section detailed discussion of effect of foam filling is summarized along with the FE investigation used for such investigations. In the last section, ‘Externally stiffened tubes’ are discussed for their application in energy absorption. Finally, summary is presented which includes what further need to be done.

2 Energy absorbers

An energy absorber is basically a system that converts kinetic energy into another form of energy. This converted energy is either reversible (e.g. pressure energy in compressible fluids and elastic strain energy in solids) or irreversible (e.g. plastic deformation energy). There exist different types of collapsible impact energy absorbers and the most common are following [21],

  1. 1.

    Tubes

  2. 2.

    Frusta

  3. 3.

    Multi-corner columns

  4. 4.

    Struts

  5. 5.

    Sandwich plates

  6. 6.

    Honeycomb cells

Apart from the abovementioned common structures, other shapes that were utilized in energy absorption include W-frame made of four rods connected by three elbows, polygonal cross-section cylinders subjected to lateral and axial loads, wave-shape guard fence made of bent pipes, cubic rod cell, three-dimensional tubular system, inversion of spherical shells and axial crushing between rigid plates, symmetric stepped circular thin-walled tube, and single-hat and double-hat thin walled sections.

Thin tubes are the most common shape and probably the oldest shape of collapsible impact energy absorbers which is attributed to their high frequency of occurrence as structural elements. In thin metallic tubes plastic energy is dissipated through several modes of deformation as [21],

  1. 1.

    Inversion

  2. 2.

    Splitting

  3. 3.

    Lateral indentation

  4. 4.

    Lateral flattening

  5. 5.

    Axial crushing

  6. 6.

    Global bending and

  7. 7.

    Progressive diamond collapse

There are three most common modes of collapse for axial compression of tube sections which are known as progressive buckling, external inversion and axial splitting as shown in figure 1 [22]. In this paper, the focus is on the progressive buckling of metallic components with particular reference to aluminium tubes. The important mechanical property of material which governs the collapse load includes stress–strain behaviour which in turn depends on the structure and heat treatment of material and vary in large range [10].

Figure 1
figure 1

Modes of collapse of hollow tubes under axial compression (a) progressive buckling, (b) external inversion, and (c) axial splitting [22].

Full size image

3 Concepts of collapse load and energy absorption

In the past, crashworthiness of a component is evaluated by utilizing several performance indicators proposed by different researchers [7, 10, 23–39]. Based on these investigations, collapse load emerged as an important design parameter of crashworthiness studies, as it is directly related to the accelerations experienced by the passengers. The instantaneous load–displacement response is obtained by measuring the load on the component–striker interface and the displacement of the striker. The area under the load–displacement curve results in total energy absorption (E ab) of the component as computed by the following equation.

$$ E_{\text{ab}} = \int_{0}^{d} {\,F(d)} \,{\text{d}}x, $$
(1)

where F(d) is the instantaneous crushing force and d is the displacement of the striker. In order to evaluate the specific energy absorption (E s), the total energy absorption is divided by the mass of the component (m c) as

$$ E_{\text{s}} = \int_{0}^{d} \,F(d) \,{\text{d}}x / m_{c}. $$
(2)

In the designing of energy absorbers, normally the oscillation of instantaneous load is ignored and the mean collapse load is computed as

$$ E_{\text{s}} = {1 \mathord{\left/ {\vphantom {1 {d\int_{0}^{d} {\,F(d)} \,{\text{d}}x}}} \right. \kern-0pt} {d\int_{0}^{d} {\,F(d)} \,{\text{d}}x}}. $$
(3)

Figure 2(a) shows the force vs. distance response and the axial force reaches an initial peak followed by a sharp drop and then oscillations. These oscillations are result of the formation of successive folding with subsequent peak corresponding to the arrival of a folding process. Sometimes, there is a secondary peak in between the two successive peaks due to local deformations. However, again the load will start to rise steeply at maximum displacement (d max) which renders the energy absorber become unusable because of the extremely high acceleration associated with the deformation process. Therefore, d max represents the maximum useful displacement of the component and more commonly termed as the stroke length. Thus, the energy absorbed is the area under this curve up to d max. Moreover, it is to be noted that for all practical purposes, the average force is often worked out as an indication of energy absorption capacity. The non-symmetric mode exhibits similar characteristics in the force–displacement curves.

Figure 2
figure 2

Typical deformation response of thin-walled tube (a) instantaneous force vs. displacement, (b) internal energy vs. displacement, and (c) mean force vs. displacement [78].

Full size image

Further, the stroke efficiency is defined as the maximum useful displacement divided by the original length of the energy absorber:

$$ S_{e} = {{d_{\hbox{max} } } \mathord{\left/ {\vphantom {{d_{\hbox{max} } } L}} \right. \kern-0pt} L}. $$
(4)

In the above equation, L is the initial length of energy absorber. An ideal energy absorber should have the quality to attain maximum force immediately after the yielding of material and maintain a constant force level throughout the entire length of the component. As a result, the energy efficiency is defined as follows:

$$ E_{e} = \frac{{E(d_{\hbox{max} } )}}{{F_{\hbox{max} } \times L}}. $$
(5)

This parameter is used to compare the different types of energy absorbers.

4 Crashworthiness by plastic collapse

When a thin-walled circular tube is subjected to axial compressive forces, it may buckle either axi-symmetrically (concertina mode) or non-axi-symmetrically (diamond mode). It was observed that thicker tubes with radius (R) to thickness (h) ratio i.e. R/h < 45 deformed axi-symmetrically. On the other hand, thinner tubes with larger R/h values deformed non-axi-symmetrically [10]. It is to be further noted that L/D ratio considerably affects the deformation modes of the tube. It has been observed that deformation mode considerably changes from concertina to Euler buckling depending upon the L/D ratio [10].

Alexander [7] proposed the first analytical expression of the quasi-static axial collapse of thin-walled cylindrical shells. If the tube folded by forming axi-symmetric rings then a concertina mode was assumed. In his analysis, the work done for deforming the metal was split into two parts, first part is required for bending at the plastic hinges and second is required for stretching the tube wall between hinges. Figure 3 presents the idealized model in his study. In this figure, during the formation of a single fold three circumferential plastic hinges occur. Assuming that the fold goes completely outwards, all the materials between the hinges experience circumferential tensile strain. The external work done is dissipated by plastic bending of three hinges and circumferential stretching of the materials in between. The equation to calculate the mean collapse load was proposed as

$$ F_{\text{m}} = K\,\sigma_{\text{y}} \,h^{1.5} \sqrt D , $$
(6)

where σ y is the yield strength of the material, K is a constant which is computed by best fit of the experimental data.

Figure 3
figure 3

Idealized axi-symmetric crushing mode of cylindrical shell [7].

Full size image

Later on Pugsley and Macaulay [40] studied about the collapse mechanism of thinner cylindrical shells. In their analysis, energy was assumed to be absorbed by plastic bending and shear of the diamond pattern. They presented a theoretical estimate of the mean axial crushing load for diamond mode of collapse as

$$ F_{\text{m}} = \sigma_{\text{y}} \,h\,(10.05\,h + 0.38\,D). $$
(7)

They proposed another model for the diamond mode based on the folding of a row of n diamonds. Using the same plastic hinge analysis as shown in Alexander’s work, the average crushing force was evaluated as

$$ F_{\text{m}} = 2.286\,n^{2} \sigma_{\text{y}} \,h^{2} , $$
(8)

where n is the number of diamond lobes formed during crushing, which depends on the D/h ratio. Generally speaking, n increases for large D/h ratio. Figure 4 shows the concertina and diamond modes of collapse for thin-walled circular tubes.

Figure 4
figure 4

Deformation modes of thin-walled circular tubes (a) concertina and (b) diamond [10].

Full size image

For square tubes under axial crushing folding mechanisms are shown in figure 5. The sequences of incidences are as follows

Figure 5
figure 5

Deformation stages in an axial crushing of thin-walled square tubes (a) local buckling, (b) rising of stress concentrations, (c) edge yielding, and (d) plastic collapse.

Full size image
  1. (i)

    At the weakest point of the tube, local buckling has begins and a slight wave appears on the tube wall

  2. (ii)

    As the collapse continues stress concentrations rise at the edges of the tube wall

  3. (iii)

    The edges of the tube wall are subjected to yield and the collapse load reaches its maximum value

  4. (iv)

    First part of the plate folds in an accordion-like mode, and

  5. (v)

    The same mechanism is followed by subsequent local buckling and folding.

As compared to the circular tubes, theoretical analysis for the static buckling of thin-walled square tubes follows the same general procedure. One of the first models was proposed by Wierzbicki and Abramowicz using super-folding element [9]. In their method, a kinematically admissible model was developed as a basic folding mechanism. This model was later modified by Abramowicz and Jones [41] to study the progressive buckling of square tubes with mean width c and wall thickness h. Two basic collapse elements were identified as illustrated in figure 6. Based on these two elements, four deformation modes were predicted i.e. one symmetric mode, one extensional mode, and two asymmetric modes.

Figure 6
figure 6

Basic collapse elements (a) type-I and (b) type II [41].

Full size image

Thus, the mean collapse load of each deformation mode can be found by equating the external work of axial crushing force to the internal work required to form either one layer of lobes with four basic collapse elements, or two adjacent layers of lobes with eight basic collapse elements. These four types of deformation modes are described next.

4.1 Symmetric mode

In the symmetric mode of deformation, two lobes on opposite sides fold inward and the other two folds outward. This mode consists of four type-I basic collapse element in one layer. This particular crushing mode is predicted to form in thin square tubes with c/h > 40.8 approximately [41]. Assuming an effective crushing distance of 0.73, the mean crushing force and the half fold length (H) of this mode are predicted using Eqs. (9) and (10) [41],

$$ \frac{{F_{\text{m}} }}{{M_{0} }} = 38.12(c/h)^{1/3} $$
(9)
$$ H = 0.99c^{2/3} h^{1/3} , $$
(10)

where M 0 is the fully plastic moment of the wall per unit length given by Eq. (11) as

$$ M_{0} = \sigma_{0} h^{2} /4. $$
(11)

where σ 0 is the flow stress of tube material. For an ideal elastic-perfectly plastic material, the flow stress is equivalent to the yield stress. Further, it is to be noted that at the expense of considerably more complicated calculations, the flow stress can be modified for strain hardening materials in this formula [9]. Abramowicz and his co-researchers theoretically developed the following equivalent flow stress denoted by σ w, to be substituted for the plastic flow stress in the theoretical expressions developed by Abramowicz and Jones [42–44] as

$$ \sigma_{\text{w}} = 2.23^{n} \frac{{\sigma_{\text{u}} }}{n + 1}\left( {\frac{2}{n + 1}} \right)^{2/3} \left( {\frac{h}{c}} \right)^{4n/9} , $$
(12)

where n is the strain hardening constant, and σ u is the ultimate tensile strength. Hanssen et al [45–47] used this formula to evaluate the mean flow stress and substituted into Eq. (9) to calculate mean crushing force of square extrusions made of aluminium alloy AA6060. Excellent agreement was found between theoretical and experimental results.

4.2 Extensional mode

Extensional mode is predicted to form in thick square tubes with c/h <7.5. It consists of four type-II folding elements in one layer. The mean crushing force and the half fold length are predicted as in Eqs. (13) and (14), respectively.

$$ \frac{{F_{\text{m}} }}{{M_{0} }} = 32.64\left( {\frac{c}{h}} \right)^{1/2} + 8.16 $$
(13)
$$ H = c^{1/2} h^{1/2} .$$
(14)

4.3 Asymmetric mixed mode A

Asymmetric mixed mode A-type consists of two layers with six type-I and two type-II folding elements. This mode of deformation is kinematically possible and has been observed by Abramowicz and Jones [41]. However, it is less often reported in literature than the previous two modes of collapse. The mean crushing load and the half fold length are evaluated as

$$ \frac{{F_{\text{m}} }}{{M_{0} }} = 33.58\,\left( {\frac{c}{h}} \right)^{1/3} + 2.92\,\left( {\frac{c}{h}} \right)^{2/3} + 2 $$
(15)
$$ H = 0.73c^{2/3} h^{1/3} . $$
(16)

4.4 Asymmetric mixed mode B

The asymmetric mixed mode B-type progressive buckling is idealized as two adjacent layers of lobes having seven type-I and one type-II basic folding elements. It is virtually indistinguishable with the symmetric mode of collapse [41]. This type of crushing is predicted to occur within the range of 7.5 ≤ c/h ≤ 40.8. The mean crushing force and the half fold length are given as

$$ \frac{{F_{\text{m}} }}{{M_{0} }} = 35.54\,\left( {\frac{c}{h}} \right)^{1/3} + 1.65\left( {\frac{c}{h}} \right)^{2/3} + 1 $$
(17)
$$ H = 0.83c^{2/3} h^{1/3} . $$
(18)

It is important to note that the exact mode of collapse observed from experiment also depends on the imperfections of the sample and is therefore very difficult to predict. Figure 7 shows the different type of deformation modes in square tubes.

Figure 7
figure 7

Deformation modes of thin-walled square tubes (a) symmetrical, (b) extensional, and (c) axi-symmetric mixed mode B [41].

Full size image

It has been commented by Jones [10] that dynamic plastic buckling happens in dynamic axial loading conditions, which is due to the structural inertia effects. In this circumstance, the deformed shape of the structure might be very different from the progressive buckling profile as illustrated in figure 8. In dynamic plastic buckling, the shell is wrinkled over the entire length and the lateral displacement field is associated with high mode numbers whereas in case of progressive folding, the wrinkling phenomenon is absent [10]. Two major effects associated with dynamic loading are the strain rate effect and the inertia effect. The strain rate effect is usually taken into account of by using material constitutive models with strain-rate sensitivity, for example the Johnson–Cook model [48].

Figure 8
figure 8

Modes of deformation in static and dynamic loading conditions (a) dynamic plastic buckling and (b) progressive folding [10].

Full size image

5 Metallic foams

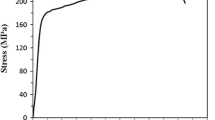
Cellular materials are typically used in cushioning, damping, insulation, construction, and many other applications [17, 19, 20, 49–52]. It is to be noted that three-dimensional cellular structures are known as foams. Foams may be either open-cell, where gas pockets connect with each other, or closed-cell, where gas forms discrete pockets, each completely surrounded by solid material. Figure 9 shows both the types of foams. Metallic foams possess a good combination of mechanical, electrical, thermal and acoustic properties [17]. In particular, the mechanical strength, stiffness and energy absorption capacity of metallic foams are much higher than those of polymer foams [51]. This presents a unique opportunity to cost-effectively increase the crashworthiness of vehicles without adding much weight. Metallic foams are attractive materials for automotive, aerospace, military and many other applications [49]. They have been used in the design of helmet and car bumper system [45–47]. Moreover, metallic foam can undergo large plastic deformation at a relatively constant load level. Figure 10 illustrates a typical compressive stress–strain response. The response closely resembles an ideal energy absorber in that the stress attains the maximum value quickly, and maintains the level over a large range of strain.

Figure 9
figure 9

Metallic foams (a) open cell and (b) closed cell [79].

Full size image
Figure 10
figure 10

Typical compressive stress–strain response of aluminium foam.

Full size image

The compressive stress–strain curve for typical closed-cell metallic foam exhibits three distinct regions i.e. linear elastic, plateau, and densification. Linear elasticity is controlled by cell wall bending and cell face stretching. The plateau region is associated with the collapse of cells and formation of plastic hinges. It is worth noting that since the foam cells collapse as the foam is squeezed, the axial compression produces very little lateral spreading, resulting in a close-to-zero Poisson’s ratio during the plastic collapse. Also, the compression of gas within each cell during the plateau stage gives a slowly rising stress–strain curve. In the densification range, cells have been completely collapsed with opposing cell walls touching each other. Further strain compresses the solid itself, giving the final region of rapidly increasing stress.

5.1 Mechanical properties of foam materials

A number of researchers have investigated the mechanical properties of foam materials. Ashby et al [17] showed that the mechanical properties of foams depend on their relative density. A power law relationship relating foam properties to the relative density was proposed as

$$ \frac{{P_{f} }}{{P_{s} }} = C\left( {\frac{{\rho_{f} }}{{\rho_{s} }}} \right)^{n} , $$
(19)

where P f is the property of the foam, P s is the property of the solid, ρ f is the foam density, ρ s is the density of the solid material, C and n are the proportionality and exponential constant, respectively. The power law equation given above has been fit to experimental data by a number of researchers using the method of least squares in order to evaluate the values of the coefficients.

6 Foam-filled tubes

The development of inexpensive closed-cell aluminium foams presents a unique opportunity to increase the crashworthiness of vehicles in a cost-effective manner [45–47, 53–58]. By filling thin-walled section with foam, the force level is significantly higher than the combined effect of empty column and foam alone. Figure 11 illustrates the interaction effect. The general expression of the axial collapse force of a foam-filled structure is given by

$$ F_{\text{m}}^{\text{tot}} = F_{\text{m}}^{\text{c}} + F_{\text{m}}^{\text{f}} + F_{\text{m}}^{\text{int}} , $$
(20)

where F totm is the mean collapse load of the foam-filled column, F cm and F fm are the mean collapse loads of empty column and foam, respectively, and F intm is the increase in mean collapse force due to the interaction effect. The mean collapse loads of column and foam are solely dictated by the material and geometrical properties. The foam–column interaction component relies on the relative stiffness of the interface and the penetration resistance of the foam layer adjacent to the outer column.

Figure 11
figure 11

Effect of foam filling on the collapse load of thin-walled columns [45–47].

Full size image

Thornton [59] was the first to report the earliest investigations on the crushing behaviour of thin-walled section filled with foam. Quasi-static and dynamic axial compressive testing of polyurethane foam-filled sections has been done by him. It was found that as compared to thickening of empty tube wall, foam filling was not weight effective. Lampinen and Jeryan [60] have done same study to verify it. The effect of polyurethane foam filler on the axial crushing of thin-walled aluminium alloy cans has been studied by Reddy and Wall [61]. It was found that the stability of crushing was improved by the presence of filler. Mantena and Mann [62] analyzed the effect of foam density for three different polymeric structural foams as fillers inside hollow steel tube. It was concluded that the lower density foams were not effective because the crushing load did not show significant improvement. Hanseen et al [45–47] experimentally studied aluminium foam-filled square aluminium columns made of 6060-T4 and 6060-T6. It was found that the transition from symmetric mode to extensional mode is dependent on the foam density as well as the tube wall thickness. An empirical expression was developed to evaluate the mean collapse load of foam-filled column:

$$ F_{\text{m}}^{\text{tot}} = 13.06\sigma_{0} c^{1/3} h^{5/3} + \sigma_{f} C_{f}^{2} + C_{\text{avg}} ch\sqrt {\sigma_{0} } \sigma_{f} , $$
(21)

where C f is the width of the foam-filler and C avg is a parameter to be determined by experimental data in order to provide best fit. Note that on the right hand side of the equation, the first term represents the column strength, the second term represents the foam strength, and the third term denotes the interaction effect.

FEM has been used extensively to study the crushing behaviour of foam-filled sections. Meguid et al [3, 4] investigated numerically and experimentally the crashworthiness of ultra light polymeric foam-filled structures. Figure 12 illustrates the FE model which was used for their numerical simulations. The tube material was aluminium with circular cross section, with a PVC foam filler of annulus cross section and density of 60 kg/m3. Comprehensive finite element simulations were conducted to investigate the effects of key geometrical parameters on the energy absorption characteristics of foam-filled columns. In their FE simulations, the foam filler’s stiffness was varied by changing the cross-sectional dimensions. It has been observed that the tube stiffness was controlled by changing the wall thickness. It was found that the relative axial stiffness of the component has a major role in the collapse behaviour of the foam-filled column. In addition, it was suggested that there exists an optimum geometrical configuration in which the maximum value of E s can be obtained.

Figure 12
figure 12

FE model geometry and contact conditions.

Full size image

Santosa and Wierzbicki [63] used explicit finite element code PAM-CRASH to examine the quasi-static axial crushing of AA6063-T7 aluminium square columns filled with aluminium foam. In particular, the strengthening mechanism of the foam filler was examined. They derived empirical relationships to calculate the mean collapse force of honeycomb-filled column (strong axis aligned with the compression axis) and that of aluminium foam filled column (strong mechanical properties in all directions) based on their numerical results as

$$ F_{\text{m}} ,h_{\text{comb}} = 14\sigma_{\text{f}} h^{5/3} c^{1/3} + c^{2} \sigma_{\text{y}} ,h_{\text{comb}} $$
(22)
$$ F_{\text{m,foam}} = 14\sigma_{\text{f}} h^{5/3} c^{1/3} + 2c^{2} \sigma_{\text{y,foam}} . $$
(23)

It was concluded that the strengthening contribution due to the lateral strength of the foam by restraining the formation of inward folds of outer column was approximately equal to that provided by the uni-axial strength of the foam. Moreover, it was suggested that a good way to leverage the foam properties to provide better energy absorption was to increase the density and strength of the foam, thus taking advantage of both mechanisms.

By foam-filling, the number of lobes on the tube wall will increase due to the elastic–plastic foundation provided by the foams to the sidewalls as shown in figure 13. Hanssen et al [45–47] have done extensive experiments to study the behaviour of square AA6060 aluminium extrusions filled with aluminium foams under quasi-static loading conditions. It was reported that the number of symmetric lobes of aluminium square columns increased from 5–6 to 8–10 due to aluminium foam filling and also most of the researchers have drawn similar conclusions [44, 64, 65].

Figure 13
figure 13

Comparison of deformation mode under quasi-static compression (a) empty column and (b) foam-filled column [80].

Full size image

When the foam core is filled within circular columns, it has been widely reported that the non-axi-symmetric mode of collapse transform to axi-symmetric mode. This is due to the restraining of the inner fold by the lateral strength of the foam. Hanssen et al [45–47] experimentally tested AA6060 aluminium extrusions filled with aluminium foam under quasi-static loading condition. Figure 14 presents one set of results corresponding to T4 temper condition and h = 1.43 mm. It was concluded that low density foam filler (0.13 g/cm3) had no effect on the deformation mode compared to the non-filled extrusions. On the other hand, noticeable shift from diamond to concertina mode was observed for higher density foam fillers (0.25 g/cm3 and 0.35 g/cm3).

Figure 14
figure 14

Mode of collapse of empty and foam-filled circular aluminium columns [80].

Full size image

It has been shown that functionally graded foam material (FGFM) is a suitable candidate for improving E s over traditional uniform density foam (UDF) [64, 66]. Nouraei [67] used LS-DYNA to analyze the crushing behaviour of aluminium columns filled with discrete functionally graded aluminium foam with different densities. The effects of various design parameters on the energy absorption characteristics were examined, such as density grading, number of grading layers, and thickness of interactive layer. It was concluded that the E s of FGFM was improved over UDF.

Numerous researchers have investigated the effect of bonding on the response of the foam-filled structure. Santosa et al [68] conducted both numerical and experimental study of aluminium foam-filled sections. It was found that the mean crushing force in the case of bonded filling can reach up to 60% higher than that of the unbounded case. However, the initial peak load also increased significantly due to the additional stiffness provided by the adhesive. Hanssen et al [45–47] also conducted research on the crushing response of square aluminium extrusions filled with aluminium foam filler. From their static crushing tests, it was reported that bonded foam filling could result in global ruptures that would suppress progressive folds and result in a drastic decrease in E s. It was cautioned that strict requirements need to be placed on the mechanical properties of foam filler, extrusion and adhesive in order to avoid fracture. A summary of their experimental results is shown in figure 14.

7 Externally stiffened tubes and optimization

Recently, plastic expansion of circular tubes by rigid inserts has been introduced as an efficient way to absorb energy without any serious sensitivity to loading direction and other external parameters [69, 70]. However, this method yields slow stroke efficiency (the ratio of deformed length to the total tube length) and E s (the ratio of total energy absorption to the tube mass) values while it requires lower values of mean crush load to protect the structure from damage. The combination of different methods of energy dissipation (inversion and axial crushing of metal tubes in a single collapsible design) was investigated for the first time by Chirwa [71].

Recently, Salehghaffari et al [72] developed a new design concept to control energy absorption characteristics of thin-walled circular tubes under an axial compression. By machining wide circumferential grooves from the outer surface of a thick-walled tube at specific intervals, they arrived at general design concept for an integrally stiffened (monolithic) tube as shown in figure 15. The thicker portions (rings) essentially act as external stiffeners for the enclosed thin-walled tube sections. When the stiffened tube is subjected to an axial compression, the thin-walled sections between two adjacent ring stiffeners fold result in enhanced energy absorption. This design model has been shown to be efficient in encouraging concertina folds, improving crushing stability, and making the component less sensitive to loading parameters, while improving its energy absorption characteristics such as an SE, maximum and mean crush forces and E s (figure 16).

Figure 15
figure 15

Results from static crushing of foam-filled components [45–47].

Full size image
Figure 16
figure 16

Externally stiffened circular tube with associated geometric design parameters [72].

Full size image

Structural optimization techniques have been applied recently to optimize energy absorption characteristics of energy absorbing components. Yamazaki and Han [73] and Chiandussi and Avalle [74] have applied an RSM (response surface method) in crashworthiness optimization of energy absorbing devices. However, the drawback of using second-order response surface (RS) models is that they may not be appropriate for creating global models that are accurate over the entire design space for highly nonlinear problems. Although it is possible to develop higher order RS models, they may not be effective or appropriate for crashworthiness optimization, partly due to the high computational cost in an extensive sampling of the design space [74]. Recent innovations to improve both the accuracy and efficiency of an RSM include the development and application of the sequential local RSM [75, 76], adaptive RSM [57], and trust-region-based RSM [77].

8 Summary and conclusions

Herein, eighty papers have been studied and comprehensive review in a simpler way is presented. The intention is to equip the designers and beginners for basic understanding the collapse mechanism of tubes. Emphasis was on the square and circular tubes under axial loading. In the axial collapse of thin-walled metallic tubes, the kinetic energy is dissipated as plastic strain energy during the formation of plastic hinges and extensional deformation of tube walls. It is to be noted that energy is to be dissipated by plastic collapse instead of being elastic. If it is elastic region only then, it will results in more damage to the occupants as no energy will be dissipated. The design of thin-walled sections are challenging due to the large deformation process and the material non-linearity. It is important to note that an ideal energy absorber must possess the following three characteristics as (i) high energy absorption, (ii) acceptable crippling load, and (iii) repeatable mode of collapse. It is important to note that while designing any energy absorber, the peak load should be relatively closer to its mean operating load so as to avoid the sudden change in acceleration experienced by the occupants. Research has shown that hollow circular and square tubes, composite tubes and multi-tube designs have been extensively used in engineering applications. However, review of the literature indicated that there is no comprehensive study of externally stiffened particularly twisted tube with and without foams. Similarly, there exists a gap in the research about change of deformation mode due to foam filling and its understanding. Effect of foam filling and their failure mechanism still need to be investigated to understand the mechanics of the crushing phenomena. Also, investigation needs to be done on the perforated tubes and to compute their energy absorption behaviour. Further, research emphasis also needs to be put on the effect of considering the foam fixity in foam filled tube.