1 Introduction

Worldwide, the thermodynamic properties of actinide dioxides are the most important properties of nuclear fuels. These oxides are widely used in nuclear reactors. The thermodynamic properties of nuclear fuels are of special interest to the fuel designers for the theoretical and experimental investigations of fuel performance. The heat capacity and thermal diffusivity are the most important parameters to calculate the thermal conductivity of actinide dioxides at an atomic level. These properties are very important to the quantum statistical theory of thermodynamic properties of solids. Some effort has been taken for the accurate calculation of the heat capacity of nuclear fuels [1,2,3,4]. Morimoto et al theoretically calculated the thermal conductivities of (U, Pu, Np)O\({}_{2}\) solid solutions based on the classical phonon transport model and compared them with the experimental results [5]. The estimation of thermal conductivity of nuclear materials has been done in the literature utilising purely analytical, experimental and numerical methods that account for all temperatures and ensure the required results [1, 5]. The heat capacities of the nuclear fuels UO\({}_{2}\) and NpO\({}_{2}\) were calculated using the series expansion relation for integer and non-integer n-dimensional Debye functions with binomial coefficients and incomplete gamma functions for integer and non-integer n-dimensional Debye functions [6]. Estimation of the heat capacity is essential to evaluate the thermal conductivity and enthalpy of the nuclear fuel. Thermal conductivity is a significant safety parameter that allows fuel temperature calculations to operate the nuclear reactor at normal conditions. Furthermore, measuring the heat capacity is required to estimate fuel behaviour during reactor transients.

Thermodynamic and transport properties of solid and liquid UO\({}_{2}\) have been reviewed and analysed by Fink in 2000 [7]. Fink developed a particularly good and rather simple approximation to the heat capacity of UO\({}_{2}\). Fink established two sets of equations to calculate the enthalpy and heat capacity of solid UO\({}_{2}\): one using exponentials and the other with polynomials. Fink chose to use only the Einstein approximation since the focus was on temperatures above the temperatures where the Debye and Einstein models deviate significantly. One important point is that Fink fits his value of the Einstein temperature to the data, rather than using a value from the literature. The high-temperature heat capacity of UO\({}_{2}\) deviates significantly from a simple Debye or Einstein description. Therefore, the high-temperature behaviour of C\(_{P}\) is dominated by processes that do not appear to be relevant in other actinide dioxides. That fact also leaves room for possible improvements on Fink’s expression to include physics that are treated very simply. Another point to be made about Fink’s work is that it started from the enthalpy and differentiated that to obtain the heat capacity, which could be important in the practical application of the work.

Thermal conductivity has been calculated for Np-oxide addition in UO\({}_{2}\) and mixed oxide fuels [8, 9]. Mixed oxide fuels comprise PuO\({}_{2}\) blended with natural or depleted UO\({}_{2}\). In the mixed oxide fuel, the ratios of PuO\({}_{2}\) and UO\({}_{2}\) are approximate, 5% and 95%, respectively. Some studies have been carried out for the evaluation of the thermal conductivity of pure NpO\({}_{2}\) [10, 11]. In 2014, Saygi evaluated the thermal conductance and heat capacities of one-dimensional nanowire systems by using Bloch–Grüneisen functions and Debye functions [12]. Basak et al simulated a UO\({}_{2}\) system using classical molecular dynamics and the interpotential parameters were found using the isothermal compressibility values from 300 to 1600 K [13]. The interatomic potential used there was generally a collective potential model comprising Bushing–Ida and Morse-type potential. The calculated lattice parameters, thermal expansivity and isothermal compressibility of UO\({}_{2}\) using the current potential parameters are in agreement with the experimental values. The Bruggeman–Fricke model was used by Webb and Charit to investigate the thermal conductivity of oxide fuels [14]. The evaluated outcomes are in agreement with the experimental data. Valhovic et al measured the thermal diffusivity of UO\({}_{2}\) from 500 to 3060 K by advanced laser-flash technique with two different set-ups [15]. The laser flash method was used to measure the thermal diffusivity and specific heat of the irradiated nuclear fuels with a laser-flash apparatus and the continuous wave laser-heating method was used for non-irradiated samples at very high temperatures. The thermal diffusivity decreases between 500 and 2000 K, then remains nearly constant up to 2700 K. Sobolev and Lemehov [16] established some useful formulas for calculating heat capacity, thermal expansion coefficient, bulk modulus and thermal conductivity of dioxides. Using phonon spectrum data, an efficient method for determining thermal conductivity and heat capacity has been established [17]. By isolating the acoustic and optic components to thermodynamic functions, several computational approaches have been developed that allow precise simulation of thermodynamic properties for a wide range of materials [18,19,20,21]. Many have investigated the thermodynamic properties of actinide dioxide nuclear fuels to enhance the properties of these materials [10, 16, 22,23,24,25]. Despite the massive increase in processing capacity, most of these purely numerical methods have some restrictions in the application.

Compared to other nuclear fuels, UO\({}_{2}\) and PuO\({}_{2}\) are generally used worldwide in almost all nuclear reactors as nuclear fuel rods. The thermal conductivity of UO\({}_{2}\) is very low that can result in localised overheating in the centres of fuel pellets. Sometimes, the mixture of UO\({}_{2}\) and PuO\({}_{2}\) is used as a mixed oxide fuel. As a result, the nuclear industry must investigate its thermodynamic properties in a wide range of conditions. Specifically, the study of severe temperature circumstances that arise inadvertently or accidentally became necessary at the earliest after many nuclear reactor accidents.

Because of international rules, the radiotoxicity of these elements and other factors, experimental research of U and Pu and their derivatives have been limited. However, for such materials, atomic simulation using computational approaches is free of these constraints. In the present study, we have calculated the isochoric heat capacity of nuclear fuels of UO\({}_{2}\) and PuO\({}_{2}\) using the collective Einstein–Debye model, in which the Debye model approximates the acoustic modes of the lattice while the Einstein model approximates the optical modes. To approximate the integral in the Debye function, we apply Simpson’s 3/8th rule to make the expression fully analytic. With the approximation expression in hand, we calculate the heat capacities using literature values for the Debye and Einstein characteristic temperatures, then compare them to the results from a variety of experimental and model-based heat capacity studies. The temperature dependence of heat capacity at constant volume, C\(_{\textrm{V}}\), is calculated using Einstein and Debye temperatures, while the heat capacity at constant pressure, C\(_{\textrm{P}}\), is measured using the thermal diffusion formula. Computational schemes are presented to demonstrate the accuracy, preciseness and efficiency of the proposed algorithm for a wide range of temperatures. Work of this type, namely developing physics-based approximations to data is, of course, very important, not only because of the insights gained from the process, but also because accurate, physics-based approximations can be expected to retain validity outside the range of the data, with the obvious caveat that such validity only applies within the same material phase.

2 Method

UO\({}_{2}\) and PuO\({}_{2}\) hold stable crystal structures (CaF\({}_{2}\)-type) [26]. The phononic heat capacity of solids as a function of temperature at constant volume can be described by the Einstein–Debye expression [21]:

$$\begin{aligned} C_\textrm{V}(T)=3N_{\textrm{A}}k_{\textrm{B}}M\left( \frac{{\theta }_\textrm{D}}{T},\frac{{\theta }_\textrm{E}}{T}\right) . \end{aligned}$$
(1)

The temperature dependence of heat capacity at constant pressure can be expressed by [27]

$$\begin{aligned} C_\textrm{P}(T)=C_\textrm{V}(T)+A_{0}{\left( C_\textrm{V}\left( T\right) \right) }^2\frac{T}{T_m}, \end{aligned}$$
(2)

where N\(_{\textrm{A}}\) is the Avogadro number, k\(_{\textrm{B}}\) is the Boltzmann constant, T is the absolute temperature, \(\theta \)\({}_{\textrm{D}}\) is the Debye temperature, \(\theta \)\({}_{\textrm{E}}\) is the Einstein temperature, \(A_0=5.1\ \times {10}^{-3\ }\mathrm {J^{-1}\ K\ {mol}}^{-1}\) and T\(_{m}\) is the melting temperature. The function M \(\left( \frac{{\theta }_\textrm{D}}{T},\frac{{\theta }_\textrm{E}}{T}\right) \) which describes the temperature dependence of \(C_\textrm{V}\) can be defined as [27]

$$\begin{aligned} M\left( \frac{{\theta }_\textrm{D}}{T},\frac{{\theta }_\textrm{E}}{T}\right) =L_{V }\left( \frac{{\theta }_\textrm{D}}{T}\right) +\left( s-1\right) A_{V}\left( \frac{{\theta }_\textrm{E}}{T}\right) . \end{aligned}$$
(3)

The first term in eq. (3) is the isochoric heat function which represents the contribution of acoustic phonons to \(C_\textrm{V}\) and the second one is that of optical phonons. In the second term, s is the total number of atoms in a single-crystalline lattice point. The function \(L_{V}\!\left( {{\theta }_\textrm{D}}/{T}\right) ,\) for n-dimensional crystalline is described by [27]

$$\begin{aligned} L_{V}\left( \frac{{\theta }_\textrm{D}}{T}\right) =n\ {\left( \frac{T}{{\theta }_\textrm{D}}\right) }^n\int ^{{{\theta }_\textrm{D}}/{T}}_0{\frac{t^{n+1}\textrm{e}^t}{{\left( \textrm{e}^t-1\right) }^2}\textrm{d}t}. \end{aligned}$$
(4)

Equation (4) represents the Debye function. For metals and alloys, generally, we take \({n} = \)3–5. Assume

$$\begin{aligned} I=\int ^{{{\theta }_\textrm{D}}/{T}}_0{\frac{t^{n+1}\textrm{e}^t}{{\left( \textrm{e}^t-1\right) }^2}\textrm{d}t}. \end{aligned}$$
(5)

Here we used the following Simpson’s 3/8th rule to determine eq. (5)

$$\begin{aligned} I&=\int ^b_a{f\left( x\right) }\textrm{d}x\nonumber \\&\approx \frac{3h}{8}\bigg \{f\left( x_0\right) +f\left( x_N\right) +3\left[ f\left( x_1\right) +f\left( x_2\right) \right. \nonumber \\&\quad \left. +f\left( x_4\right) +\dots +f\left( x_{N-2}\right) +f\left( x_{N-1}\right) \right] \nonumber \\&\quad +2\left[ f\left( x_3\right) +f\left( x_6\right) +\dots +f\left( x_{\frac{N}{3}-1}\right) \right] \bigg \}, \end{aligned}$$
(6)

where

$$\begin{aligned}{} & {} h=\frac{b-a}{N},\quad a=x_0,\\{} & {} {x}_1=a+h,\quad {x}_2=a+2h, \ldots , \quad b=a+Nh. \end{aligned}$$

One can rewrite eq. (6) alternately as the sum of values

$$\begin{aligned}&I=\ \int ^b_a{f\left( x\right) }\textrm{d}x\approx \frac{3h}{8}\nonumber \\&\quad \times \left\{ f\left( x_0\right) +f\left( x_N\right) +\sum ^{N-1}_{i\left( \ne 3k\right) =1}{f\left( x_i\right) +\sum ^{\frac{N}{3}-1}_{j=1}{f\left( x_{3j}\right) }}\right\} . \end{aligned}$$
(7)

In eq. (5), let

$$\begin{aligned}&f\left( t\right) =\frac{t^{n+1}\textrm{e}^t}{{\left( \textrm{e}^t-1\right) }^2}, \end{aligned}$$
(8)
$$\begin{aligned}&f\left( t_0\right) =f\left( 0\right) ={{\mathop {\textrm{lim}}_{t\rightarrow 0} \frac{t^{n+1}\textrm{e}^t}{{\left( \textrm{e}^t-1\right) }^2}\ } \rightarrow \frac{0}{0}}. \end{aligned}$$
(9)

Apply L’ Hopital’s rule as follows:

$$\begin{aligned} f\left( 0\right)&={\mathop {\textrm{lim}}_{t\rightarrow 0} \frac{\left( n+1\right) t^n\textrm{e}^t+t^{n+1}\textrm{e}^t}{2\left( \textrm{e}^t-1\right) \textrm{e}^t}\ }\rightarrow \frac{0}{0} \end{aligned}$$
(10)
$$\begin{aligned} f\left( 0\right)&={\mathop {\textrm{lim}}_{t\rightarrow 0} \frac{\ \left( n+1\right) nt^{n-1}+(n+1)t^n}{2\ \textrm{e}^t\ }=0\ }. \end{aligned}$$
(11)

Applying Simpson’s 3/8th rule in eq. (5), we get the following result:

$$\begin{aligned} I&=\ \int ^b_a{f\left( x\right) }\textrm{d}x\approx \frac{3h}{8}\nonumber \\&\quad \times \left\{ f\left( x_N\right) +3\sum ^{N-1}_{i\left( \ne 3k\right) =1}{f\left( x_i\right) +2\sum ^{\frac{N}{3}-1}_{j=1}{f\left( x_{3j}\right) }}\right\} . \end{aligned}$$
(12)

In eq. (3), the second term \(A_{V}\!\left( {{\theta }_\textrm{E}}/{T}\right) \) is the Einstein function, determined by the following relation [26]:

$$\begin{aligned} A_{V}\left( \frac{{\theta }_\textrm{E}}{T}\right)&={\left( \frac{{\theta }_\textrm{E}}{T}\right) }^2\frac{\textrm{e}^{{({\theta }_\textrm{E}}/{T)}}}{{\left( \textrm{e}^{{({\theta }_\textrm{E}}/{T)}}-1\right) }^2}\ \nonumber \\&=\ {\left( \frac{{\theta }_\textrm{E}}{2T\,\textrm{sinh}\left( \frac{{\theta }_\textrm{E}}{2T}\right) }\right) }^2. \end{aligned}$$
(13)
Fig. 1
figure 1

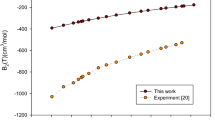
The temperature dependence of heat capacity for UO\(_2\) (\(\theta _\textrm{D} = 377\) K, \(\theta _\textrm{E} = 535.8\) K, ref. [35]).

Full size image

3 Numerical results and discussion

In the present study, an analytical method was proposed to evaluate the isochoric and isobaric heat capacities of the nuclear fuels UO\({}_{2}\) and PuO\({}_{2}\) as a function of temperature using Einstein–Debye model and thermal diffusion formula, respectively. We have calculated the isochoric and isobaric heat capacities of UO\({}_{2}\) and PuO\({}_{2}\) using three different sets of integer values (n \(=\) 3.4, 3.8 and 4.0). We have constructed a program for the computation of heat capacity by using Python language. Simpson’s 3/8th rule has been taken into account for the easy calculation of heat capacity. The results are plotted for the integer and non-integer values of n \(=\) 3.4, 3.8 and 4.0 and compared with other previously published experimental outcomes [28,29,30,31,32,33,34]. A rigorous review of the thermophysical properties of UO\({}_{2}\) and mixed oxide fuels was conducted and the best thermophysical property correlation was chosen in [32]. The solidus and liquidus temperatures of UO\({}_{2}\) and PuO\({}_{2}\), thermal expansion and density, enthalpy and specific heat, enthalpy of fusion and thermal conductivity are among the properties examined by Carbajo et al [32]. The temperature dependence of computational results and results obtained from the literature (Arima et al [28], Yun et al [29], Eser et al [31] and Chu et al [34]) are compared in figures 1 and 2 for \(C_\textrm{V}\) and \(C_\textrm{P}\) of nuclear fuels. The parameter value n reported in the literature is taken to be from 3 to 5 for nuclear fuels, nanomaterials and semiconductor samples. We note that the calculation by Eser et al [31] does not perform a particularly good job of reproducing the experimental data so that there is room for improvement that could likely be accomplished with relatively little effort. As shown in figures 1 and 2, the best-fitting curve for the relevant analytical \(C_\textrm{V}\) and \(C_\textrm{P}\) data can be achieved. The consistency of the method with standard computational and literature results demonstrates that the results are suitable.

In figure 1, the temperature dependence of isochoric and isobaric heat capacities of UO\({}_{2}\) nuclear fuels are estimated between 100 and 3000 K and compared with the results for previous reports [28, 29, 31]. UO\({}_{2}\) and PuO\({}_{2}\) are isostructural and they form solid solutions. When compared to conventional UO\({}_{2}\) fuel, the minor fraction of PuO\({}_{2}\) in mixed oxide fuel will alter the thermophysical properties of mixed oxide fuels marginally [32]. The heat capacity results are almost consistent in the vicinity of 500 K. The maximum deviation of heat capacity is obtained with ref. [31] as shown in figure 1. The fitting techniques are performed using eqs (1) and (2) and plots obtained with the parameter values for nuclear fuels UO\({}_{2}\) (\(\theta _{\textrm{D}} =377\) K, \(\theta _\textrm{E} = 535.8\) K) [35] and N = 900 is taken for more accurate values. As can be seen from figure 1, the calculated heat capacities in the present study were consistent with the literature reports (Arima et al [28] and Yun et al [29]) at low temperatures.

In figure 2, the temperature dependence of isochoric and isobaric heat capacities of PuO\({}_{2}\) nuclear fuel is evaluated between the same temperature ranges 100–3000 K and compared with the previously published reports [28, 31, 34]. In this figure, the results are in agreement at the low-temperature range but, the deviation is more at the high-temperature range. This deviation might be due to many effects like Schottky and the exciting terms. However, \(N = 900\) is taken for more accurate values for PuO\({}_{2}\) sample (\(\theta {}_{\textrm{D}}=415\) K, \(\theta _{\textrm{E}} = 571\) K) [35] and N \(=\) 900. The results obtained for \(C_\textrm{V}\) (\({n} = 4.0\)) and \(C_\textrm{P}\) (\({n} = 3.4\)) were found to be more consistent with the results found in Arima et al [28] and Chu et al [34], respectively. Arima et al [28] extensively carried out molecular dynamics (MD) simulations for some thermal properties of uranium nitride (UN), PuN, UO\({}_{2}\) and PuO\({}_{2}\), such as thermal expansion, ionic diffusion and heat capacity. Chu et al [34] performed molecular statics and molecular dynamics simulations to investigate the entropy and enthalpy of PuO\({}_{2}\) and \(\alpha \)-Pu\({}_{2}\)O\({}_{3}\), as well as their heat capacity and thermal expansion.

Evaluated heat capacities \(C_\textrm{V}\) and \(C_\textrm{P}\) as a function of temperature in the present study were consistent with the previous literature data. As we relatively compare the theoretically evaluated \(C_\textrm{V}\) and \(C_\textrm{P}\), the latter shows higher values than \(C_\textrm{V}\). However, some results are not in agreement at high temperatures for UO\({}_{2}\) fuel which shows that high temperatures are unsuitable when compared to average nuclear reactor core temperatures. Finally, one can see that the proposed method in this study reveals preciseness and efficiency. Furthermore, this method is reliable to evaluate the heat capacity of nuclear fuels for a variety of samples. The proposed method can be used for studying experimental results of nuclear fuels.

Fig. 2
figure 2

The temperature dependence of heat capacity for PuO\(_2\) (\(\theta _\textrm{D} = 415\) K, \(\theta _\textrm{E} = 571\) K, ref. [35]).

Full size image

4 Conclusion

In this work, the temperature dependence of isochoric heat capacity C\(_\textrm{V}\) for nuclear fuels UO\({}_{2}\) and PuO\({}_{2}\) were evaluated by a precise novel method based on the Einstein–Debye approximation while isobaric heat capacity C\(_\mathrm{P\ }\)was evaluated by the thermal diffusion formula in a wide range of temperatures. Here, the acoustic modes of the lattice are approximated by the Debye model while the optical modes are approximated by the Einstein model. This method is extremely adaptable, with no restrictions on how it might be applied to study the thermophysical properties of the nuclear fuel. It was observed that the proposed method based on Simpson’s 3/8th rule is entirely novel for integer and non-integer values of parameter n and reveals the stability of the method for UO\({}_{2}\) and PuO\({}_{2}\) nuclear fuels. The results from the proposed method is in agreement with the other literature results which can be used to estimate the other thermodynamic properties of nuclear fuels. The efficacy of the analytical approach is well-known and acclaimed for its computational convenience and precision, as well as its full comprehension of related physical facts. The consistency of the method with standard computational and literature results, as well as its stability, were found to be satisfactory for UO\({}_{2}\) and PuO\({}_{2}\) nuclear fuels.