The influence of temperature and composition on the crystal properties of Al$_{1-x}$B$_{{x}}$N semiconducting ternary alloys

Abstract

Structural parameters, energy band gaps, electronic charge density, phonon modes and transport properties of Al$_{1-x}$B$_{x}$N ternary alloys in the hypothetical zinc-blende structure are investigated using first-principles total-energy calculations. The authors’ results show that by adding more B atoms into AlN, the material under focus becomes less compressible, less ionic and its energy band gap still ($\Gamma$-X) indirect for all alloy compositions x of interest exhibiting a bowing parameter of 1.24 eV. The calculated phonon density of states indicates soft modes for B contents in the interval 0.5 $\le x\le$ 0.8 suggesting thus non-dynamical stability of the ground-state phase in this composition range. The temperature dependence of structural and transport properties is examined and discussed. The thermal conductivity of cubic BN at 300 K is recorded as 0.862 kW/m$\cdot$K showing a very good accord with the experimental values reported in the literature.

1 Introduction

Wide band-gap binary nitride materials are of great interest and are intensively used for the fabrication of optical and electronic devices. This mainly originates from their tremendous optoelectronic and thermal properties [1,2,3,4,5,6,7,8,9,10,11,12]. These materials adopt cubic zinc-blende (ZB) as well as hexagonal wurtzite structures. Alloying these materials makes it possible to tune the band-gap energy accurately, which permits the construction of novel materials with desirable fundamental properties by adjusting the alloy composition. This is because many physical properties of these alloys change continuously between the values of the corresponding parent compounds [13, 14]. Consequently, by alloying BN with AlN, we obtain Al$_{1-x}$B$_{x}$N ternary semiconductor alloys. These alloys may offer many possibilities for device engineering and can cover a wide range of wavelength acting in the ultraviolet range [15,16,17]. A possible merge of high resistivity and excellent chemical and thermal stabilities makes AlN and BN suitable materials to be used as passivation layers for semiconductor devices.

Current activities in optoelectronic devices have led to significant interest in studies of electronic, dynamical and thermal properties of materials. Thermal expansion is connected with thermal properties. It also influences many other fundamental properties, such as the variation of the energy band gap with temperature, internal electric field and device lifetime. Moreover, the knowledge of the thermal expansion coefficient is especially important for epitaxial growth [18,19,20,21,22]. Regarding ternary nitride semiconductors, different studies were dedicated to the calculation of the structural and electronic properties of these materials [8]. The present work deals with various fundamental properties of Al$_{1-x}$B$_{x}$N ternary alloys with emphasis on their dependences on composition and temperature. These include elastic, piezoelectric, vibrational and transport properties. The objective of this work is to show how these properties change when varying the alloy composition x in the zinc-blende Al$_{1-x}$B$_{x}$N with different compositions, ranging from 0 to 1 and the temperature in the interval 0–600 K. The calculations were carried out within the virtual crystal approximation (VCA) using ab-initio pseudopotential calculations in the generalised gradient approximation (GGA) based on density functional theory (DFT) and density functional perturbation theory (DFPT) which may impart considerable information related to the properties of these alloys. Wherever possible, our findings are compared with the previous theoretical calculations and experimental results. The rest of the manuscript is arranged as follows. In §2 we report in brief the computational details of our calculations. In §3 the results regarding the structural, electronic, vibrational, thermodynamic and thermoelectric properties of zinc-blende Al$_{1-x}$B$_{x}$N alloys are analysed and compared with other theoretical calculations and experimental findings. Concluding remarks are summarised in §4.

2 Computational details

The calculations were performed using DFT [23, 24] within the plane-wave basis set and pseudopotentials implemented in the abinit package [25]. Exchange correlation of GGA is used to describe the interaction energy of the electrons [26]. The interactions between electrons and core ions are simulated with Troullier–Martins norm-conserving pseudopotentials [27]. The electron states considered in valence states are B-2s$^{2}$2p$^{1}$, Al-3s$^{2}$3p$^{1}$ and N-2s$^{2}$2p$^{3}$. The energy cut-off of the plane-wave expansions was chosen as 160 Ry. The special points sampling integration over the Brillouin zone was employed with 6$\times$6$\times$6 mesh using the Monkhorst–Pack method [28]. The equilibrium structural parameters, namely lattice constants (a) and bulk modulus (B), were derived from total energy against the unit cell volume plot, then by fitting to the Birch–Murnaghan equation of state [29]. The elastic constants ($C_{ij})$ were obtained using DFPT [30,31,32,33] from the second derivatives of the total energy concerning the strain perturbation [34]. The piezoelectric tensor components $e_{ij}$ were consecutively calculated from the second derivatives of the total energy concerning strain and electric field. Phonon calculations have been executed by using the DFPT within the linear response approach [35,36,37]. The dynamical matrices have been computed, then Fourier-transformed to real space and hence force constants are established and employed to determine phonon frequencies at different k points of the Brillouin zone [35,36,37]. The alloy is simulated for the compositions x ($0\le x\le 1)$ by applying the VCA [38]. The VCA is a docile way of studying configurationally disordered systems. In the VCA approach, the atoms A and B are replaced by a single kind of pseudoatom C, which linearly averaged the crystal potential of those of A and B. The thermodynamic properties of Al$_{1-x}$B$_{x}$N ternary alloys at various compositions x, are obtained using the quasi-harmonic Debye model approach included in Gibbs code [39]. Seebeck coefficient and thermal conductivity are obtained using the Boltztrap code [40]. The thermal transport properties were computed using a dense mesh of 40$\times$40$\times$40 k-points in the BZ. The transport parameters calculated in the BoltzTraP code use constant relaxation time approximation. Thus, the electronic part of the thermal conductivity appears with relaxation time. To extract the real values of these quantities, we need to evaluate carrier relaxation time. The carrier relaxation time can be calculated by using the following expression as reported in ref. [41]:

$$\begin{aligned} \tau =\left( \frac{2}{m^{*}k_{\mathrm {B}}T} \right) ^{3/2}\frac{\pi ^{1/2}{\hbar }^{{4}}C_{ii}}{3D^{2}}=A_{x}T^{-3/2}, \end{aligned}$$

(1)

where the direction-dependent elastic constants ($C_{ii})$ of a cubic crystal can be defined as follows [41]:

$$\begin{aligned} C_{ii}= & {} C_{11} \,\mathrm{in} \,\left( 100 \right) , \end{aligned}$$

(2)

$$\begin{aligned} C_{ii}= & {} \frac{1}{2}\left( C_{11}+C_{12}+2C_{44} \right) \,\mathrm{in} \,\left( 110 \right) , \end{aligned}$$

(3)

$$\begin{aligned} C_{ii}= & {} \frac{1}{3}\left( C_{11}+2C_{12}+4C_{44} \right) \,\mathrm{in}\,\left( 111 \right) , \end{aligned}$$

(4)

$\langle c_{ii}\rangle$ the average value of $C_{ii}$ for three different directions of propagation.

D is the deformation potential defined as

$$\begin{aligned} D=a_{0}\frac{\partial E_{g}}{\partial a}. \end{aligned}$$

Here, $E_{g}$ is the change of band energy with the change of lattice parameters (a). Precise effective masses m* tensor eigenvalues of the lowest conduction band structure at the X point, obtained from DFPT [42] for BN are 0.3015, 0.3015 and 0.9164 in units of electron mass and thus the average effective mass is 1/(1/ $m^*_{\mathrm {BN}})=$ 0.3883. As for AlN effective mass tensor eigenvalues, they are 0.3272, 0.3272 and 0.5281 and 1/(1/ $m^*_{\mathrm {AlN}})=$ 0.3747. Note that the average effective mass for BN and AlN is almost the same. The effective mass of the Al$_{1-x}$B$_{x}$N ternary alloys is assumed to follow Vegard’s law.

3 Results and discussion

Table 1 Equilibrium lattice parameter a, bulk modulus $B_{0}$ and its pressure-derivative $B_{0}^{\prime }$ for Al$_{1-x}$B$_{x}$N$\, \left( 0\le x\le 1 \right) \,$ternary alloys.

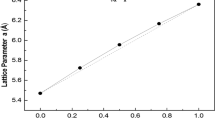
The equilibrium structural parameters are determined by fitting the curves that represent the variation in the total energy vs. the volume for Al$_{1-x}$B$_{x}$N ternary alloys (0 $\le x \le \,$1) in the hypothetical zinc-blende structure to the Birch–Murnaghan equation of state. The procedure is similar to that used in refs [43,44,45]. Our results regarding the equilibrium lattice parameter $a_{0}$, bulk modulus $B_{0}$ and its first-pressure derivative ${B_{0}^{\prime }}$ for zinc-blende Al$_{1-x}$B$_{x}$N at various alloy compositions x in the interval 0–1 are given in table 1. For comparison, we show also the data available in the present literature. We remark from table 1 that our results regarding $a_{0\, }$ agree very well with those of experiment [46] for both parent compounds of the alloy system of interest. Moreover, they are closer to the experiment [46] than the theoretical results reported in ref. [48]. For $x=0.50$, our result agrees very well with that reported by Kumar et al [48]. For other alloy concentrations x $(0<x< 1)$, our results are predictions. As far as $B_{0}$ and $B_{0}^{\prime }$ are concerned, our findings are for reference. Note that $B_{0}$ of AlN is much smaller than that of BN. This indicates that BN is less compressible than AlN.

Fig. 1

Relative lattice parameter (a/$a_{0})$ against temperature for Al$_{1-x}$B$_{x}$N ternary alloys.

Fig. 2

Relative bulk modulus ($B$ $/$ $B_{0})$ against temperature for Al$_{1-x}$B$_{x}$N ternary alloys.

Table 2 Elastic constants ($C_{ij}^{\prime })$ and $T^{-3/2}$ relaxation time coefficients $A_{x}\,$of Al$_{1-x}$B$_{x}$N$\, \left( 0\le x\le 1 \right) \,$ternary alloys.

Our obtained equilibrium lattice parameters a(x) and bulk modulus $B\left( x \right)$ for zinc-blende Al$_{1-x}$B$_{x}$N at various alloy compositions x in the interval 0–1 can be fitted to a least-squares procedure giving the following expressions:

$$\begin{aligned}&a(x)=4.383-0.138\, x-0.617\, x^{2} \end{aligned}$$

(5)

$$\begin{aligned}&B\left( x \right) =198.856-75.874\, x+235.981\, x^{2}. \end{aligned}$$

(6)

The quadratic terms in eqs (5) and (6) are the bowings of the lattice constant and the bulk modulus respectively. The magnitude of the quadratic term in eq. (5) confirms the non-linear behaviour of the lattice constant a as a function of x. The deviation of the structural parameters from linearity (non-obedience to the Vegard’s Law) in ternary semiconductor alloys is due principally to the lattice mismatch between the lattice constants of AlN and BN. However, one can notice that for other alloys like Zn$_{1-x}$Cd$_{x}$S [50], Si$_{1-x}$C$_{x}$, Si$_{1-x}$Ge$_{x}$ and Si$_{1-2x}$C$_{x}$Ge$_{x}$ [51] (0 $\le x \le$ 1) the investigation has been done based on first-principles calculations where lattice parameters have taken a linear dependence with the composition and follow the Vegard’s law.

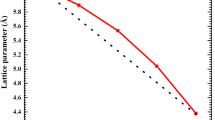
Figure 1 shows the variation of the relative lattice parameter ($a$ $/$ $a_{0})_{\, }$with temperature for Al$_{1-x}$B$_{x}$N for various concentrations of B from 0 to 1. We remark that for a given alloy concentration x, $a$ $/$ $a_{0\, }$remains almost constant up to the temperature 100–150 K (depending on x) and augments rapidly thereafter. This indicates that by increasing temperature up to 600 K, the lattice parameter increases as well, especially in the temperature interval 150–600 K. This is true for all alloy compositions with x ranging from 0 to 1.

Fig. 3

Direct ($\Gamma$-$\Gamma$) and indirect ($\Gamma$-X) and ($\Gamma$-L) band-gap energies along with the valence bandwidth against composition x for Al$_{1-x}$B$_{x}$N ternary alloys.

The evolution of the relative bulk modulus ($B$ $/$ $B_{0})$ as a function of temperature in Al$_{1-x}$B$_{x}$N ternary system for x ranging from 0 to 1 is plotted in figure 2. Note that by raising the temperature to 100 K, B/$B_{0}$ remains almost constant ($B$ $/$ $B_{0}=1$, i.e. $B=B_{0})$, then it decreases quickly by enhancing the temperature beyond 100 K up to 600 K. The decrease of $B$ $/$ $B_{0}$ by enhancing the temperature in the interval 100–600 K means that the bulk modulus B decreases. The decrease of B by increasing the temperature in the range 100–600 K suggests that the stiffness of the material under focus becomes lower when the temperature is enhanced beyond 100 K up to 600 K. This statement is true for all alloy compositions with x ranging from 0 to 1. Nevertheless, one should note that B becomes less important when the temperature is increased. Therefore, we can conclude that one can combine x and the temperature to obtain the desired bulk modulus of the material under focus.

The elastic properties of semiconducting materials are interesting quantities that are linked to several fundamental properties of these materials which include inter-atomic potentials and phonon spectra, to name a few [52,53,54,55,56]. For that, the elastic constants of Al$_{1-x}$B$_{x}$N have been computed using GGA approach. Our findings regarding the elastic constants of Al$_{1-x}$B$_{x}$N for different B contents are collected in table 2. Data existing in the present literature are also presented for comparison. The accord between our results and those of the literature is generally reasonable. Note that the $C_{ij}$s obtained using the LDA approach [17] are closer to the experiment [55] than those obtained using the GGA approach (present work).

The knowledge of the electronic properties of semiconducting materials is a piece of important information that can allow a precious synthesis of these materials and the fabrication of devices based on them [59,60,61,62,63,64]. In this work, the electronic band structure of Al$_{1-x}$B$_{x}$N, assuming zinc-blende structure has been computed for x ranging from 0 to 1 using the GGA approach.

The variation of the conduction band edges at $\Gamma$, X and L with respect to the top of the valence band as a function of B content for the Al$_{1-x}$B$_{x}$N ternary alloy system is shown in figure 3. Also shown in the same figure is the evolution of the valence bandwidth (VBW) as a function of x. Note that all direct and indirect energy band gaps increase monotonically and in a non-linear way with an increase in the concentration of B in Al$_{1-x}$B$_{x}$N. The same conclusion can be drawn for the VBW vs. B content. The alloy system under focus seems to be an indirect band-gap ($\Gamma$-X) semiconductor for all B concentrations in the interval 0–1. Our results yielded values of 3.35 and 4.52 eV for $\Gamma$-X of AlN and BN, respectively. The ($\Gamma$-X) band-gap bowing parameter is found to be 1.24 eV, whereas that of ($\Gamma$-$\Gamma$) band gap is estimated to be 5.73 eV. These parameters are induced by composition disorder. The trend in the VBW is generally related to the ionicity character of the crystal [65]. In general, as the VBW becomes wider, the semiconductor material becomes less ionic. In our case (figure 3), the VBW increases by enhancing B in Al$_{1-x}$B$_{x}$N. This suggests that the crystal of interest becomes less ionic when going from AlN to BN. This is consistent with the Phillips ionicity scale [66] which shows that the ionicity of BN (with an ionicity factor of 0.221) is smaller than that of AlN (with an ionicity factor of 0.449).

In their study of the elastic modulus, optical phonon modes and polaron properties in Al$_{1-x}$B$_{x}$N ternary alloys, Bouarissa and Saib [17] have reported that the Fröhlich coupling parameter in Al$_{1-x}$B$_{x}$N becomes almost constant in the alloy composition ranging from 0.5 to 0.8. In the present work, we have presented the phonon density of states for Al$_{1-x}$B$_{x}$N for x ranging from 0 to 1 in figure 4. Our results show that in the alloy composition range 0.5–0.8, some phonon frequencies are negative indicating that the material system under focus is dynamically unstable in the composition range 0.5–0.8 ($0.5\le \, x\, \le 0.8)$.

Fig. 4

Phonon density of states (DOS) for Al$_{1-x}$B$_{x}$N ternary alloys at different compositions x.

A crystalline structure is stable if it fulfils two conditions: its elastic constant, $C_{ij}$, obeys the Born criterion and all its phonon mode frequencies are positive (dynamical stability). The cubic crystal of the zinc-blende system has three separate elastic constants: $C_{11}$, $C_{12}$ and $C_{44}$; the stability criteria follow the ensuing formulas,

$$\begin{aligned} C_{11}-C_{12}> 0; C_{11} \quad + 2C_{12}> 0\quad \mathrm{and}\quad C_{44}> 0. \end{aligned}$$

(7)

Fig. 5

Valence electron charge density of Al$_{1-x}$B$_{x}$N ternary alloys at different compositions x.

Fig. 6

Seebeck coefficient against temperature for Al$_{1-x}$B$_{x}$N ternary alloys.

Table 3 Lattice parameters a, bulk modulus B, carrier relaxation time $\tau$, Seebeck coefficient S and thermal conductivity $\kappa _{e}\,$ at 300 K for Al$_{1-x}$B$_{x}$N $\left( 0\le x\le 1 \right)$.

Single-crystal elastic constants are evaluated and shown in table 2. Applying Born criteria to our results, it appears that, it is out of all studied concentrations of Al$_{1-x}$B$_{x}$N. Our system is mechanically stable. From the phonon density of states, we conclude that Al$_{1-x}$B$_{x}$N is dynamically unstable in the composition range 0.5–0.8 ($0.5\le \, x\, \le 0.8)$. Thus, it is verified that our zinc-blende structure of Al$_{1-x}$B$_{x}$N is stable when $0\le x<0.5$ and $0.8<\, x\, \le 1$. To confirm other structures, a similar study is needed.

The physics of the chemical bond is very important in making a general distinction between ionic and covalent bonding in semiconducting materials [66, 67]. On the other hand, the investigation of electron charge density in semiconductors may provide useful information regarding the chemical bonding properties and interstitial impurities in the materials under focus [68,69,70,71]. In this work, the valence electron charge density is computed for the material system in question. Our results for zinc-blende Al$_{1-x}$B$_{x}$N ternary semiconductor alloys at various concentrations x $(0\le x\le 1)$ are displayed in figure 5. Note that for zinc-blende AlN ($x=\,$0), an important electric charge quantity is lying between the atomic sites and at the anion site. This indicates the presence of mixed-covalent-ionic bonding. Nevertheless, the top of the electron charge distribution is located nearer to the anion site than to the cation site. This suggests that the contribution to the formation of chemical bonding comes essentially from the anion. When more B atoms are added in AlN, the amount of charges becomes more important and the maximum of the electron charge density increases and shifts slightly towards the cation. This reflects the change in the ionicity character of the material system under focus.

The evolution of the Seebeck coefficient as a function of temperature for Al$_{1-x}$B$_{x}$N when x varies in the interval 0 to 1 is shown in figure 6. Note that by enhancing the temperature from 0 to 1000 K, the Seebeck coefficient increases or decreases (depending on the B concentration x) up to around 300 K, then it approaches a constant value between 0.23 and 0.25 mV/K when the temperature is beyond 300 K. For good efficiency, materials with high Seebeck coefficient are required. The use of these materials represents one among several important factors for the efficient behaviour of thermoelectric generators and thermoelectric coolers. Physically speaking, the Seebeck coefficient in both magnitude and sign is in some sense the entropy per unit charge in the material.

The $T^{-3/2}$ relaxation time coefficients at various alloy compositions x are given in table 2. Table 3 reports the values of relaxation time at 300 K expressed in seconds for the material under focus for x ranging from 0 to 1. The evolution of the thermal conductivity per relaxation time against temperature obtained from the use of BoltzTrap code for Al$_{1-x}$B$_{x}$N ternary alloys at various B contents x in the interval 0–1 is depicted in figure 7. For a given alloy composition x, the thermal conductivity per relaxation time remains almost constant when the temperature is augmented up to 200 K. Beyond this temperature and up to 1000 K, the thermal conductivity per relaxation time increases rapidly and in a non-linear way showing an upward bowing. This is true for all alloy compositions x.

Fig. 7

Thermal conductivity per relaxation time against temperature for Al$_{1-x}$B$_{x}$N ternary alloys.

Fig. 8

Thermal conductivity against temperature for Al$_{1-x}$B$_{x}$N ternary alloys.

The temperature dependence of the thermal conductivity in Al$_{1-x}$B$_{x}$N is illustrated in figure 8 for various values of x $(0\le x\le 1)$. We remark that for a given x, the thermal conductivity is highly increased with rising temperature in the interval 0–1000 K. Qualitatively, the behaviour of the thermal conductivity against temperature is similar for all alloy compositions x. However, from the quantitative point of view, the magnitude of the thermal conductivity depends strongly on x. The heat conductivity in Al$_{1-x}$B$_{x}$N is essentially attributed to lattice vibrations (phonons). The increase of the thermal conductivity with increasing temperature means that the heat transfer occurs at a higher rate when the temperature is raised. Correspondingly, materials of high thermal conductivity can be widely used in heat sink applications. The determined thermal conductivity for Al$_{1-x}$B$_{x}$N at 300 K is presented in table 3. By referring to this table, one can note that the obtained thermal conductivity of 0.862 kW/m$\cdot$K for cubic BN is in very good accord with the experimental values 0.768 and 0.940 kW/m$\cdot$K reported in ref. [72]. Due to the lack of data regarding the thermal conductivity of Al$_{1-x}$B$_{x}$N $(0\le x< 1)$, to the authors’ best knowledge, the present findings are predictions. However, one should note that the values obtained for these materials in this work exceed the overall thermal conductivity of metals.

4 Conclusions

The structural, elastic, electronic, optical, vibrational and thermoelectric properties of Al$_{1-x}$B$_{x}$N ternary alloys with emphasis on their dependence on composition and temperature were investigated. The computations were performed using first-principles total energy calculations. A hypothetical zinc-blende structure was assumed for all compositions x $(0\le x\le 1)$. The authors’ results showed that by enhancing the B content, the material system of interest becomes less compressible. The variation of the energy band gaps against composition x showed that the material under focus remains an indirect ($\Gamma$-X) band-gap semiconductor for all x in the range 0–1 and it exhibits a bowing parameter of 1.24 eV. The evolution of VBW against x suggested that the crystal ionicity of the material system in question decreases when going from $x=0$ (AlN) to $x=1$ (BN), indicating that BN is less ionic than AlN which is consistent with the Phillips ionicity scale. The phonon density of states indicated soft modes in the composition range $0.5\le x \le 0.8$ which suggests non-dynamical stability of the ground state phase in this range. The temperature dependence of structural parameters and thermoelectric properties such as carrier relaxation time, Seebeck coefficient and thermal conductivity was analysed and discussed. The thermal conductivity of cubic BN at 300 K is recorded as 0.862 kW/m$\cdot$K. This accords well with the experiments.