Theoretical investigation of structural, electronic and thermoelectric properties of $p{-}n$ type $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system

Abstract

Based on the density functional theory and the Boltzmann transport theory, the thermoelectric properties of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ solid solution with $x= 0.25, 0.5 \hbox { and } 075$ were investigated. The calculated structural parameters were in good agreement with the previous work and the mechanical and dynamical stabilities were confirmed. The electronic band structure computed using the Tran-Blaha-modified Becke and Johnson (TB-mBJ) exchange potential indicated that the band gap can be tuned by the alloy effect. We combined first-principles calculations and the semiclassical Boltzmann transport theory by considering the electronic transport in the $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ solid solution to determine the effect of varying the Sn composition on the thermoelectric performance. Our results have shown exceptionally high electrical conductivity for ${\hbox {Mg}}_{2}\hbox {Sn}$ and higher Seebeck coefficient for $\hbox {Mg}_{2}\hbox {Si}$. The highest figure of merit (ZT) was predicted for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ solid solution with $x = 0.5$ where ZT has reached 0.55 with carrier concentration charge $n = 10^{20}\hbox { cm}^{-3}$ (p-type doping) at intermediate temperatures. Consequently, the alloying system with p-type doping may improve the thermoelectric properties compared to the $\hbox {Mg}_{2}\hbox {Si}$ and $\hbox {Mg}_{2}\hbox {Sn}$ pristine compounds.

1 Introduction

New alternative sources of energy as an alternative to the limited and polluted energy from oil, nuclear reactions, wood and natural gas are the need of the hour because of the growing demand of energy in different industrial sectors. Nowadays considerable efforts are made to produce energy from sustainable sources [1,2,3,4,5]. Thermoelectricity offers the possibility to transform heat into electricity which is an important source of renewable and sustainable energy as far as the ecological aspects are concerned. Thermoelectric materials should play a greater role in the near future to contribute in sustainable development [6,7,8,9].

Recently, thermoelectric phenomenon has attracted so much attention in industry due to the discovery of new materials that could generate energy from the wasted heat in common materials. The conversion efficiency of thermoelectric systems depends on the combination of opposite properties, called the figure of merit (ZT). ZT is calculated as $\hbox {ZT}=(S^{2} \sigma / K)T$, where T is the absolute temperature, S is the Seebeck coefficient, $\sigma$ is the electrical conductivity and K is the thermal conductivity [10, 11]. It has been very difficult to increase $\hbox {ZT}\,{>}\,1$ because an efficient thermoelectric performance depends on the ability to generate a potential difference by Seebeck effect, drive an electric current, and maintain a temperature gradient between the hot source and the cold one [4].

For a long time, the limits in the thermoelectric performance has restricted industrial applications such as in space (radio isotope generator for space probes) and electronics (refrigeration using Peltier modules). However, since late 1990s the emergence of new thermoelectric concept has achieved significant advances leading to improved thermoelectric performance [12].

The most commonly used thermoelectric material at low temperatures (150–200 K) is an alloy made of bismuth and antimony, such as $\hbox {Bi}_{1-x}\hbox {Sb}_{x}$. This has shown better thermoelectric performance with n-type doping than with p-type doping. So far the bismuth tellurium alloy ($\hbox {Bi}_{2}\hbox {Te}_{3}$) was the most investigated thermoelectric material both experimentally and theoretically [13].

Furthermore, the antimony and tellurium alloy ($\hbox {Sb}_{2}\hbox {Te}_{3}$) which has the same crystalline structure as the $\hbox {Bi}_{2}\hbox {Te}_{3}$ alloy [14] has shown an interesting thermoelectric performance operating at intermediate temperature. Besides, the lead telluride (PbTe) and lead tin alloys (PbSn) which have shown an optimised and tunable band gap for thermoelectric conversion achieved a better thermoelectric performance around 700 K [15]. On other hand, the ${\hbox {Mg}}_{2}\hbox {X}$ system has attracted the interest of the thermoelectric scientific community due to the abundance of these elements in nature and non-toxicity [16].

The compounds of the silicide family are more involved in the fabrication of thermoelectric devices [17]. The silicide family has more interesting thermoelectric applications [18]. Furthermore, because of their high specific strength and elastic modulus, they have been used in aerospace applications and automobiles as optical fibres due to their good ohmic contact with Si [19].

The $\hbox {Mg}_{2}\hbox {Si}$ and $\hbox {Mg}_{2}\hbox {Sn}$ compounds are crystallised in a cubic face centred structure (Fm-3m) with antifluorite-type and their lattice parameters are: 6.39 Å for $\hbox {Mg}_{2}\hbox {Si}$ and 6.765 Å for $\hbox {Mg}_{2}\hbox {Sn}$ indicating an indirect band gap for both materials [16]. Due to a large difference in mass between $\hbox {Mg}_{2}\hbox {Si}$ and $\hbox {Mg}_{2}\hbox {Sn}$, it was found that their solid solutions have a lower thermal conductivity. Therefore, the $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ alloy might present more interesting features which may lead to better thermoelectric performance. Recent experimental works have reported that $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ solid solutions may achieve better thermoelectric performance with n-type doping [20].

Thus, in this report we aim to investigate the physical properties such as structural, electronic and transport properties of the $\hbox {Mg}_{2}\hbox {Si}$, $\hbox {Mg}_{2}\hbox {Sn}$ compounds and $\hbox {Mg}_{2}\hbox {Si}_{1-{x}}\hbox {Sn}_{{x}}$ ($x= 0.25, 0.5 \;\text {and}\; 0.75$) alloy system with different charge carrier concentrations (n- and p-type doping) to explore the alloy and doping effects on the thermoelectric performance. We employed the density functional theory (DFT), using the full potential- linearised augmented plane waves (FP-LAPW) method. The paper is organised as follows: In §2, we detail the computational considerations and technical data useful for modelling. In §3, we present our main calculated results and discussed them in light of available experimental and theoretical works. We report our major findings in §4.

2 Computational methods

Ab-initio calculations were performed using the FP-LAPW method implemented in the Wien2k code [21]. To describe the exchange-correlation potential we adopted the GGA approximation with the PBE parametrisation [22] combined with the Tran-Blaha modified Becke and Johnson (TB-mBJ) potential [23] to avoid the underestimation of the band gap with the simple Perdew–Burke–Ernzerhof-generalised gradient approximation. For the Brillouin zone sampling, we used a Monkhorst and Pack mesh [24] with k-mesh of $12\times 12\times 12$ and well-converged basis sets with $R_{\mathrm{MT}}K_{\mathrm{max}} = 7$ where $R_{\mathrm{MT}}$ and $K_{\mathrm{max}}$ are the smallest muffin-tin radius and the maximum size of the reciprocal lattice vectors, respectively. The maximum value for partial waves inside the atomic spheres is $l_{\mathrm{max}} = 10$. We have optimised and relaxed the structures until the minimum of the energies were reached and the forces in the solid solutions ($x=0.25, 0.5$ and 0.75) were less than 1 mRy / au. An initial calculation with a supercell of $2\times 2\times 2$ confirmed that there is no preferential site for the two atoms Si and Sn in the solid system. The structural, electronic and elastic properties were calculated from the conventional cell (8 atoms of Mg and 4 atoms of Si or Sn). The mechanical stability of the system was investigated through the calculation of the elastic modulus by applying small strain to the equilibrium unit cell and determining the corresponding variations in the total energy. The dynamical stability of the system was calculated through the phonon dispersion using finite displacement technique as implemented in PHONOPY code [25] with a $2 \times 2 \times 2$ supercell. The thermoelectric transport properties such as the electrical conductivity ($\upsigma$), Seebeck coefficient (S) and electronic thermal conductivity ($K_{\mathrm{ele}}$) were obtained by solving the linearised Boltzmann equation within the relaxation time approximation as implemented in the BoltzTraP code [26]. This is based on the fact that the electrons contributing to transport are in a narrow energy range due to the delta-function like Fermi broadening. For such a narrow energy range, the relaxation time is nearly the same for the electrons. The accuracy of this method has been well tested earlier, and the method actually turns out to be a good approximation [27, 28].

Table 1 Structural parameter of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system.

Fig. 1

Lattice constant of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system as a function of Sn concentration.

Table 2 Elastic moduli C11, C12 and C44 (in GPa) of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system.

3 Results and discussion

3.1 Structural and electronic properties

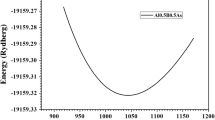
Full optimisation of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ structures were initiated from the experimental lattice parameters. The computed optimised lattice parameters were reported in table 1 with the theoretical results and available experimental data in order to compare them. Our calculated structural parameters are in good agreement with the experimental and the theoretical work [3, 16]. It can be seen from figure 1 that the ground-state lattice constant increases linearly with the Sn substitution, following Vegard’s law fairly well:

$$\begin{aligned}&{} { at }(x) = 6.76\,{*}\,x + 6.39\,{*}\, (1 - x), \end{aligned}$$

(1)

$$\begin{aligned}&{} { ar}(x) = 6.82\,{*}\,x+ 6.38\,{*}\,(1 - x), \end{aligned}$$

(2)

where at and ar are the theoretical (according to the Vegard’s law) and our experimental lattice parameters respectively. From the Vegard’s law we obtained the basic lattice parameter for different concentrations ($x=0.25, 0.5 \hbox { and } 0.75$) and calculated their optimised parameter. We attach great importance to the structural parameter and atomic position (optimisation of forces for the solid solution is necessary due to the change of atomic position) because accurate structural parameters lead to an accurate estimation of the physical properties.

Fig. 2

Phonon dispersion curves of (a) $\hbox {Mg}_{2}\hbox {Si}$, (b) $\hbox {Mg}_{2}\hbox {Si}_{0.5}\hbox {Sn}_{0.5}$ and (c) $\hbox {Mg}_{2}\hbox {Sn}$ and the total and partial phonon DOSs of (d) $\hbox {Mg}_{2}\hbox {Si}$, (e) $\hbox {Mg}_{2}\hbox {Si}_{0.5}\hbox {Sn}_{0.5}$ and (f) $\hbox {Mg}_{2}\hbox {Sn}$.

The elastic properties of the $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system were calculated to confirm their mechanical stability. The elastic constants for a cubic structure are reduced to three constants ($C11,~C12\,$ and C44) because of its symmetry. Our computed results are listed in table 2. To be considered as mechanically stable, the cubic structures must fulfill the following requirements on the elastic constants: $C11>0$, $C44>0$, $C11>{\vert }C12{\vert }$ and ($C11+2C12)>0$. The elastic stiffness constants of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ satisfy the above conditions implying that the considered alloys are mechanically stable. The present computational results are in good agreement with the previous reports [29, 30].

Besides, we calculated the phonon spectrum density to confirm the dynamical stability of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system. Figures 2a–2c show the phonon dispersion curves for $\hbox {Mg}_2\hbox {Si}_{1-x}\hbox {Sn}_{x}$ alloys. Note that the calculated phonon band of the alloy system ($x=0.25, 0.5$ and 0.75) has shown a similar behaviour. Due to the fact mentioned in the previous paragraph we shall present only the $x\,{=}\,0.5$ concentration as illustration. No imaginary phonon frequency was found in the whole BZ for all the systems, which supports the dynamical stability of this system. The increase of the Sn concentration led to a decrease in the phonon frequency. This can be explained by the difference in atomic masses between the Si and Sn elements. However, the coupling is the strongest between the acoustical and optical branches because the atomic masses are similar for Mg and Si. The large difference of atomic masses between Mg and Sn lead to more efficiency of the phonon scattering, thus decreasing the lattice part of thermal conductivity. To better understand the contributions of each atom in the phonon frequency, the total and partial phonon densities of states are displayed in figures 2d–2f. The low-frequency modes below 4 THz were mainly dominated by Sn, whereas the high-frequency modes (above 7 THz) were dominated by Si. The frequency ranges (4–6 THz) are dominated slightly by the Mg atom. The partial phonon DOS of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ alloys system indicates that Sn atoms contribute more to the low-frequency region than Si and Mg atoms because Sn is heavier than the other two atoms. The contribution of the Si atoms is in high frequencies due to the strong bond with Mg compared to Sn.

Fig. 3

Electronic band structures of (a) $\hbox {Mg}_{2}\hbox {Si}$, (b) $\hbox {Mg}_{2}\hbox {Si}_{0.5}\hbox {Sn}_{0.5}$ and (c) $\hbox {Mg}_{2}\hbox {Sn}$ and the total and partial electronic DOSs of (d) $\hbox {Mg}_{2}\hbox {Si}$, (e) $\hbox {Mg}_{2}\hbox {Si}_{0.5}\hbox {Sn}_{0.5}$ and (f) $\hbox {Mg}_{2}\hbox {Sn}$.

Figures 3a–3c show the calculated band structures of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ alloys. Note that here also we presented only the $x=0.5$ concentration as illustration since the alloy system has shown a similar magnitude. As mentioned earlier, generally the PBE-GGA functional underestimates the band gap. For instance, $\hbox {Mg}_{2}\hbox {Sn}$ has shown a metallic character with the simple PBE-GGA. Thus, the TB-mBJ potential leads to the accurate estimation of the band gaps. Our calculations of the electronic band structure using TB-mBJ potential for $\hbox {Mg}_{2}\hbox {Si}$ and $\hbox {Mg}_{2}\hbox {Sn}$ has shown an indirect band-gap semiconductor character. The valence band maximum (VBM) was located at the T-point while the conduction band minimum (CBM) was located at the X-point. Interestingly, an indirect to direct band gap transition occurs for $x = 0.25, 0.5$ and 0.75 alloy compositions where the CBM moves from T-points to X-point while the VBM remains at the T-points. This may lead to an increase in the mobility of charges indicating that the band gap can be tuning by the alloy effect. The calculated band-gap values for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ alloys, as well as experimental data and theoretical results are shown in table 3. Besides, to better understand the atomic contribution to the electronic band structure we also study the density of electronic states (DOS) for $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ alloys system as shown in figures 3d–3f. The valence region $-5$ to 0 eV are dominated by the s and p states of Mg with the p state of Si (Sn). One can observe in this interval a slight superiority of the p states of the Si atoms which is due to the strong bond of Si with Mg in comparison with Sn. In the conduction region we observe the domination of the p state of Si (Sn) and a contribution of the s and p states of the Mg atoms.

Table 3 Band-gap values of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system.

3.2 Thermoelectric properties

The variation of the transport properties of the $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ alloys with respect to temperature and carrier concentration $n=10^{19}$, $10^{20}$ and $10^{21}\hbox {cm}^{-3}$ (p- and n-types) was estimated from simulations using BoltzTraP code [26]. On the basis of the calculated band structure, we estimated the electrical conductivity $(\sigma )$ with the constant scattering time relaxation ($\tau$) approximation from the ratio $\sigma /\tau$. The relaxation time $(\tau )$ can be determined by comparing the experimentally measured electrical conductivity $(\sigma )$ [10, 29].

The relaxation time rests on both temperature and charge carrier concentration (n) using the standard electron–phonon relation, given by $\tau = C\times T^{- 1}n^{-1/3}$, where C is a constant to be determined from experimental data [10]. We estimated C to be $1.21496\times 10^{-5}$ and $8.24883 \times 10^{-5}$ for $\hbox {Mg}_{2}\hbox {Si}$ and $\hbox {Mg}_{2}\hbox {Sn}$ respectively [31] and $2.0807\times 10^{-5}$, $1.16933\times 10^{-5}$ and $1.13612\times 10^{-5}$ for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ solid solution ($x=0.25, 0.5 \hbox { and } 0.75$) [29, 35].

Fig. 4

Evolution of the electrical conductivity with respect to the temperature for different carrier concentrations with (a) representing the p-type and (b) the n-type, obtained for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system.

After the determination of $\tau$ we present now the evolution of electrical conductivity of $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ alloys as a function of temperatures and different carrier concentrations as displayed in figure 4. We can see that the electrical conductivity decreases as temperature increases with p and n carrier concentrations. This behaviour is mainly due to the reduction of electron mobility at high temperatures except for the low concentration doping level ($n=10^{19}\hbox { cm}^{-3}$). The electrical conductivity of $\hbox {Mg}_{2}\hbox {Sn}$ is remarkably higher and increases as the carrier concentration charges increase from $1000\hbox { S}/\hbox {cm}\,(10^{19}\hbox { cm}^{-3})$ at 300 K to 25000 S / cm ($10^{21}\hbox { cm}^{-3}$) at 300 K for p- and n-types, which may be explained by the lower band gap of $\hbox {Mg}_{2}\hbox {Sn}$. Note that the large difference of $\sigma$ (S / cm) between $\hbox {Mg}_{2}\hbox {Sn}$ and $\hbox {Mg}_{2}\hbox {Si}$ is reported previously in [32]. Besides, one can remark that $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ with $x=0.25$ ($n=10^{19}$ and $10^{20}$, with n-type doping) has shown a higher value of $\upsigma$ than the p-doping level. The electrical conductivity of the $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ alloy system is dependent on temperature and carrier concentration charge at the same time. For instance, the electrical conductivity of $\hbox {Mg}_{2}\hbox {Sn}$ is larger than that of the other materials [33] at room temperature and intermediate temperature. It was comparable for the $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ solid system and the $\hbox {Mg}_{2}\hbox {Si}$ compound. One may expect that the ZT of the $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ alloy system will reach its maximum near the intermediate temperature as in the previous work [33], a high ZT was reached in the range of 700 K.

Fig. 5

Evolution of the Seebeck coefficient with respect to the temperature for different carrier concentrations with (a) representing the p-type and (b) the n-type, obtained for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system.

Figure 5 shows the calculated Seebeck coefficient (S) as a function of temperature for the $\hbox {Mg}_{2}\hbox {Si}_{1-{x}}\hbox {Sn}_{{x}}$ solid solutions in different carrier concentrations (p- and n-types). The sign of Seebeck coefficient follows the type of doping carrier concentration charge and indicates whether the material is p- or n-type. We found that the absolute value of the Seebeck coefficient increases with an increase in temperature except at low carrier concentration, $n=10^{19}\hbox { cm}^{-3}$ where it decreases above 600 K. We also found that the Seebeck coefficient reaches its maximum value (in absolute value) for low carrier concentration $n =10^{19}\hbox { cm}^{-3}$. It reached $500\,\mu \hbox {V}/\hbox {K}$ for the p-type $\hbox {Mg}_{2}\hbox {Si}$ at 650 K due to a slight increase in the charge concentration (holes) and the strong binding nature of Si–Mg in $\hbox {Mg}_{2}\hbox {Si}$ compound. However, for the high carrier concentration ($n=10^{20}$ and $10^{21}\hbox { cm}^{-3})$, although the Seebeck coefficient has increased linearly as a function of temperature (from 300 to 900 K), it has decreased as the carrier concentration increased ($n=10^{20}$ and $10^{21}\hbox { cm}^{-3})$.

Fig. 6

Evolution of the electronic thermal conductivity $(K_\mathrm{e})$ with respect to the temperature for different carrier concentrations with (a) representing the p-type and (b) the n-type, obtained for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system.

Fig. 7

Evolution of the ZT with respect to the temperature for different carrier concentrations with (a) representing the p-type and (b) the n-type, obtained for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system.

Now we turn our attention to the thermal conductivity, where both lattice and electronic parts can contribute to the total thermal conductivity. However, a low thermal conductivity is compulsory to keep the temperature gradient. The thermal conductivity ($K_{\mathrm{Total}}=K_{\mathrm{ele}}+K_{\mathrm{L}}$) consists of two parts: electronic and phonon contribution. It is a complicated task to compute lattice thermal conductivity ($K_{\mathrm{L}}$) from the ab-initio calculations. Therefore, in the present work, $K_{\mathrm{L}}$ is considered as a constant parameter independent of temperature and carrier concentration [34]. The measured thermal conductivity undergoes small variations of about 10 to 20%, in the temperature range 300–800 K [35]. The lattice part of the thermal conductivity was found to be 7.9 and 5.9 W / m K for ${\hbox {Mg}}_{2}{\hbox {Si}}$ and $\hbox {Mg}_{2}{\hbox {Sn}}$ respectively [34, 35]. For the $\hbox {Mg}_{2}{\hbox {Si}}{-}{\hbox {Sn}}$ alloy system, we shall take $K_{\mathrm{L}}$ as fixed ($K_{\mathrm{L}}=1.25\hbox { W}/{\hbox {m}}\,{\hbox {K}}$) from the previous thermal lattice measurement of a different $\hbox {Mg}_{2}\hbox {Si}{-}\hbox {Sn}$ solid solution in which $K_{\mathrm{L}}$ had shown similar magnitude as a function of the variation of the alloy concentration [16]. Now we focus on the electronic part within the constant time relaxation ($\tau$), which is calculated using the Boltzmann approach as implemented in BoltzTraP code [26]. The electronic part of the thermal conductivity, $K_{\mathrm{ele}}=K_{\mathrm{ele}}(T, n$), was determined using the same electron lifetime $\tau$. The electronic thermal conductivity ($K_{\mathrm{ele}}$) for $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ alloys as a function of temperatures and for constant chemical potential is presented in figure 6. Note that $K_{\mathrm{ele}}$ for $\hbox {Mg}_{2}\hbox {Sn}$ has larger values than for other compounds, reach 25 W / m K at 800 for $n = 10^{21}\hbox { cm}^{-3}$ (n-type). This is due to the high electrical conductivity of the material and the mobility of the charge carriers. However, at low temperatures $K_{\mathrm{ele}}$ has a marginal contribution to $K_{\mathrm{Total}}$ compared to $K_{\mathrm{L}}$. We noticed a significant increase of $K_{\mathrm{ele}}$ for $\hbox {Mg}_{2}\hbox {Sn}$ above 400 K while for the other compounds $K_{\mathrm{ele}}$ was almost constant for the whole temperature range (300–900 K), while the $\hbox {Mg}_{2}\hbox {Si}$ compound has shown a lower value of $K_{\mathrm{ele}}$ which was comparable to other optimal thermoelectric materials operating at high temperature [33]. Therefore, the $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ solid system has led to a decrease in the lattice thermal conductivity and $\hbox {Mg}_{2}\hbox {Sn}$ has shown a higher electronic thermal conductivity while $\hbox {Mg}_{2}\hbox {Si}$ has exhibited a lower electronic thermal conductivity. Since the thermoelectric performance is based on the compromise between the high electrical conductivity and low thermal conductivity one may expect that the $\hbox {Mg}_{2}\hbox {Si}_{x}\hbox {Sn}_{1-x}$ solid system will enhance the thermoelectric conversion efficiency.

After determining all the thermoelectric coefficients we turn our attention to ZT. According to figure 7, $\hbox {Mg}_{2}\hbox {Si}_{0.5}\hbox {Sn}_{0.5}$ exhibits a maximal thermoelectric performance throughout the carrier concentration range $n= 10^{19}$ to $10^{21}\hbox { cm}^{-3}$ (p- and n-types). Except for the concentration $n = 10^{19}$ n-type, the maximum value of ZT is obtained to be 0.6 for $x= 0.25$. In particular, $\hbox {ZT} = 0.53$ can be reached at 800 K for $\hbox {Mg}_{2}\hbox {Si}_{0.5}\hbox {Sn}_{0.5}$ with a carrier concentration of $10^{20}\hbox { cm}^{-3}$ (p-type). The value of ZT has increased significantly for the whole temperature range (300–900 K) for all compounds except for $\hbox {Mg}_{2}\hbox {Si}$. This later shows a constant behaviour for ZT when temperature changes. Therefore, the increase in the charge carrier concentrations (up to $n = 10^{20}\hbox { cm}^{-3})$ mainly with p-type doping has led to a considerable enhancement in the thermoelectric performance of the $\hbox {Mg}_{2}\hbox {Si}{-}\hbox {Sn}$ materials compared to the pristine $\hbox {Mg}_{2}\hbox {Si}$ and $\hbox {Mg}_{2}\hbox {Sn}$ compounds.

4 Conclusion

In summary, we have investigated the thermoelectric properties of $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ solid solution with $x{=}\,0.25$, $0.5 \,\hbox {and}\, 0.75$ using full potential-linearised augmented plane wave (FP-LAPW) method and Boltzmann transport theory. The calculated structural parameter was found to be in good agreement with the experimental data and the mechanical and dynamical stabilities of all the systems were confirmed. The electronic band structure was calculated using the TB-mBJ potential which shows more accurate results and found to be in good agreement with the previous work indicating that the band gap may be tuned by the alloy system. The transport properties were computed using the semiclassical Boltzmann theory. $\hbox {Mg}_{2}\hbox {Sn}$ has displayed higher electrical conductivity while $\hbox {Mg}_{2}\hbox {Si}$ has shown larger value of Seebeck coefficient. A thorough analysis of the behaviour of transport coefficient with effects of temperature and charge concentrations were reported and discussed. Finally, a ZT value of 0.53 was reached at 800 K for $\hbox {Mg}_{2}\hbox {Si}_{0.5}\hbox {Sn}_{0.5}$ with a carrier concentration of $10^{20}\hbox { cm}^{-3 }$ (p-type) at intermediate temperatures. Thus, based on our results the alloy system $\hbox {Mg}_{2}\hbox {Si}{-}\hbox {Sn}$ may improve the thermoelectric performance compared to the pristine $\hbox {Mg}_{2}\hbox {Si}$ and $\hbox {Mg}_{2}\hbox {Sn}$ compounds due mainly to the reduction of the lattice thermal conductivity caused by the alloying system. The p-type doping has shown an optimal thermoelectric performance in this alloying system. This may lead to future work on p-type $\hbox {Mg}_{2}\hbox {Si}_{1-x}\hbox {Sn}_{x}$ system such as the band-gap engineering through strain effect and the nanostructuration leading to an enhancement of their thermoelectric performances.