1 Introduction

The physical meaning of thermal diffusivity is associated with how fast the heat spreads, when the temperature varies with time [1]. Velocity-based estimations of thermal diffusivity (TD) are well known. In the macroscopic approach, Angstrom introduced the velocity of a ‘steady periodic temperature-wave’ to estimate thermal conductivity of solids [2]. King [3] has modified the heat source and estimated both thermal conductivity and thermal diffusivity based on the velocity of periodically oscillating temperature waves. Recently, the use of step-temperature excitation ‘position-dependent velocity of a single non-effective temperature point and a single effective temperature point’ for the estimation of thermal diffusivity of solid was reported by Settu Balachandar et al [4,5]. In the microscopic level, Einstein [6] related ‘the mean square spread of the temperature point’ with thermal diffusivity of solids. Debye [7] explained the thermal transport property of dielectric solids based on phonons; ‘the average velocity of gas particles’.

Several optical and non-optical methods have been utilized for measuring the TD of optically transparent solids. Some of the popular methods are flash method [8], thermal lensing [9], interferometric technique [4,5,10–12], photoacoustic technique [13], photothermal deflection technique [14,15] etc. Recently, Settu Balachandar et al reported a two-beam interferometer which separates a unique isothermal surface in a transient temperature profile and measures its velocity. The magnitude of the isothermal surface is predicted using the thermo-optic coefficient of the solid to estimate the thermal diffusivity of dielectric solids [4,5].

In this article, a conceptually new approach is proposed to estimate the TD of optically transparent dielectric bulk solids at ambient temperature based on the instantaneous velocity of isothermal surfaces, using a self-reference interferometric technique.

The proposed analytical model is as follows.

2 Analytical treatment

During one-dimensional (1D) unsteady heat flow, the temperature anywhere in the heat-affected region varies both with space and time, satisfying [2]

$$ \alpha \frac{\partial^{2}T\!{\kern-.5pt}\left( {x,t} \right)}{\partial x^{2}}=\frac{\partial T\!{\kern-.5pt}\left( {x,t} \right)}{\partial t}. $$
(2.1)

Using the chain rule we can rewrite eq. (2.1) as

$$ \alpha \cdot\frac{\partial^{2}T(x,t)}{\partial x^{2}}=\frac{\partial T(x,t)}{\partial x}\cdot\frac{\partial x}{\partial t}, $$
(2.2)
$$ \alpha =v{}\left[ {\frac{\left( {{\partial T(x,t)}/{\partial x}} \right)}{({{\partial^{2}T(x,t)}/{\partial x^{2}}} )}} \right], $$
(2.3)

where v = ∂ x/∂ t is the speed /velocity.

Step-temperature excitation is popular because it is simple. If T(x,t) is the temperature disturbance that propagates to a depth x in time t s, then the non-dimensional temperature for such an excitation is given by [2]

$$ {\Theta} =\text{erfc}(\eta ) $$
(2.4)

where

$$ {\Theta} =\frac{T(x,t)-T_{i}} {T_{H} -T_{i}} $$
(2.5)

and

$$ \eta =\frac{x}{\sqrt {4\alpha t}} . $$
(2.6)

From eq. (2.4),

$$ \eta =\text{inverfc}({\Theta} ), $$
(2.7)

where erfc is the complementary error function, T H is the step temperature at x = 0, T i is the initial temperature, Θ is the non-dimensional temperature, η is the similarity variable, and inverfc is the inverse complementary error function. The first-order and second-order differentials of the temperature profiles can be used to estimate velocity [4,5].

Velocity v can be written as

$$ v=\left( {\frac{x}{2t}} \right)\!. $$
(2.8)

This equation implies that step-temperature excitation exhibits position-dependent velocity and the said velocity is equal to the instantaneous velocity of that isothermal surface at a given location. The proof is as follows:

Consider a moving temperature point T(x,t) in the heat ray path resulting from step-temperature excitation for two different instants of time t 1 and t 2 (0<t 1<t 2). The corresponding location of this temperature point is at x 1 and at x 2 respectively. Using eqs (2.4) and (2.6) this can be rewritten as follows:

$$ {\Theta} =\text{erfc}\left( {\frac{x_{1}} {\sqrt {4\alpha t}_{1}} } \right)=\text{erfc}\left( {\frac{x_{2}} {\sqrt {4 \alpha t_{2}} } } \right), $$
(2.9)
$$ \eta =\left( {\frac{x_{1}} {\sqrt {4 \alpha t}_{1}} } \right)=\left( {\frac{x_{2}} {\sqrt {4 \alpha t_{2}} } } \right). $$
(2.10)

The LHS of eqs (2.9) and (2.10) implies that for the given Θ, η is constant and time invariant i.e., x and the square root of t vary but the ratio remains constant; the equation above then becomes

$$ \frac{x_{1}} {\sqrt {t_{1}} } =\frac{x_{2}} {\sqrt {t_{2}} } . $$
(2.11)

Let

$$ x_{2}=x_{1}+{\Delta} x $$
(2.12)

and

$$ t_{2}=t_{1}+{\Delta} t . $$
(2.13)

Rearranging, we get

$$\begin{array}{@{}rcl@{}} \frac{t_{1} +{\Delta} t}{t_{1}} =\left[ {1+\frac{\Delta x}{x_{1}} } \right]^{2}. \end{array} $$

Using the binomial approximation, the equation above can be written as

$$\frac{\Delta t}{t_{1}} =\frac{2{\Delta} x}{x_{1}} . $$
$$ \text{Instantaneous velocity}=v=\frac{\Delta x}{\Delta t}=\left( {\frac{x_{1}} {2t_{1}} } \right)\!. $$
(2.14)

Equation (2.14) implies the instantaneous velocity of the temperature point. It tallies with the velocity given in eq. (2.8). Using eqs (2.6) and (2.7),

$$2\eta^{2}=\left( {\frac{v x}{\alpha} } \right)\!. $$

The thermal diffusivity is given by

$$ \alpha =\left( {\frac{vx}{2\eta^{2}}} \right)\!. $$
(2.15)

3 Experimental set-up of self-reference interferometer

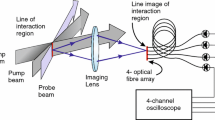
The schematic diagram of the experimental set-up is shown in figure 1. The experimental set-up consists of a laser source, a microscopic objective, a pin hole with an observer plane, a camera, a Peltier heater and a solid sample. When a monochromatic light source is switched ON, the light passes through the microscopic objective and the pin hole produces a ‘slowly diverging laser beam’ which falls onto the sample surface. One beam reflected from the front surface of the sample and ‘the other beam refracted from the front surface, passing through the sample medium and reflected from the back surface’ of the sample interfere with each other and form an interference pattern. The fringe pattern is concentric circles with non-uniform spacing. Thus, an optically transparent solid sample is utilized to form self-reference interferometer. The intensity at the centre of the fringe system (bright /dark) and the size of the fringe pattern are governed by the wavelength of the source and the optical configuration, i.e., the distance between the source and the sample, the refractive index of the media (air and sample) and thickness of the sample. The intensity at the centre of the fringe system indicates a point in a fixed plane (inside the sample) away from the heat source and the experiment will be stopped before the heat disturbance reaches the said fixed plane to ensure the boundary condition that the solid is semi-infinite.

Figure 1
figure 1

The schematic diagram of the self-reference interferometer.

Full size image

Let the initial intensity at the centre of the fringe system is maximum, i.e., the initial path difference is made experimentally equal to multiples of 2 π and is given by [5]

$$ I_{{\max}}=4I_{0}(\cos((2\pi d(n_{0}))/\lambda )^{2}), $$
(3.1)

where λ is the wavelength of the laser source, n 0 is the refractive index of the plate, d is the thickness of the sample, and I max is the maximum intensity at the centre of the fringe system at an ambient temperature. The change in intensity at any point due to a transient heat flow is given by

$$ I_{\text{change}}=4I_{0}(\cos((2\pi(d+ {\Delta} d)(n_{0}+{\Delta} n))/\lambda )^{2}). $$
(3.2)

The change in the refractive index due to the thermal expansion Δd of the sample, and the temperature-dependent refractive index Δn is given by

$$ {\Delta} n =(\partial n/\partial T){\Delta} T_{C}. $$
(3.3)

The thermal expansion coefficient is 8.3×10−5/∘C and the thermo-optic coefficient ∂ n/∂ T reported for BK7 is 0.27×10−5/∘C and it is linear from an ambient temperature to 125 ∘C [16].

4 Experimental result

1D unsteady heat flow is established via step-temperature excitation. Peltier heat is switched ON and the desired temperature T H is pre-set (by adjusting the power supply). The experiment starts when the sample surface is suddenly kept in thermal contact with the heater. Due to the heat flow inside the solid, the intensity pattern changes which is recorded using a CCD camera. Two frames are sampled at known intervals of time shown in figure 2. In the sampled interferogram, the portion of interest is cropped. The corresponding normalized intensity profile at two instants of time is plotted against the pixels (shown in figure 3).

Figure 2
figure 2

The interferogram at different instants of time t 1 and t 2 during 1D unsteady heat flow via step-temperature excitation (from left to right) for BK7 sample.

Full size image
Figure 3
figure 3

The normalized intensity profile along heat ray path at t 1 and t 2 s for the BK7 sample.

Full size image
Figure 4
figure 4

The plot of ‘the product of experimentally measured instantaneous velocity with its distance’ vs. normalized intensity of the quartz sample.

Full size image

Three intensity points are considered in the linear region, using eq. (2.14). Instantaneous velocity is estimated from the knowledge of the time elapsed Δt and the predicted shift in location Δx via the calibration of the sample under the given optical configuration. Estimate 2 η 2 using eq. (4.1).

$$ 2\eta^{2}=2\{\text{inverfc}({\Theta} )\}^{2}. $$
(4.1)

The experimental data are as follows: BK7 glass is used as the specimen. The frames are taken at t 1 = 1 s and t 2 = 3 s; so Δt = 2 s. T H = 29.5∘C T i = 24∘C, ΔT H = 5.5∘C. The wavelength of the laser is 632.8 nm, d, the length of the sample is 8 mm, n = 1.515. The measured instantaneous velocities from the experiment are 0.169 mm /s, 0.156 mm /s and 0.13 mm /s. The predicted values of 2 η 2 are 2.3, 2.1, and 1.7 respectively. The thermal diffusivity of the solid is estimated from eq. (2.15). The value obtained from the proposed method is 0.56 mm 2/s and the reported value is 0.548 mm 2/s [17].

Under identical experimental conditions, the same experimental procedure is adopted for the quartz glass specimen. But another approach is introduced; which does not involve thermo-optic coefficient, 2 η 2, thermal expansion etc. Consider a linear region in normalized intensity points obtained via the experiment shown in figure 4 (here 0.5 to 0.8 was considered), and the position of the corresponding intensity points. The thermal diffusivity is obtained from the slope of ‘the product of instantaneous velocity of normalized intensity points and its corresponding distance’ vs. normalized intensity points. The thermal diffusivity value obtained from the proposed method is 0.88 mm 2/s and the reported value is 0.91 mm 2/s [11]. It closely tallies with the literature value.

The advantages of the proposed interferometric approach are as follows: there is hardly any alignment problem, the fringes are non-localized with a huge contrast and the size of the pattern can also be altered. There is also flexibility in altering the intensity pattern at the centre of the fringe system, and flexibility in fixing the distance between the sample and the detector. This approach is highly sensitive to the change in refractive index within the sample because the probe beam travels twice in the sample medium and thermal compensation for the reference beam is not required. The proposed interferometric approach requires fewer parameters to be measured, and it is not necessary that the sample should have highly polished surfaces, and perfect parallelism.

5 Conclusion

The instantaneous velocity of isothermal surfaces based estimation of the thermal diffusivity is proposed and demonstrated using a self-reference interferometer. The proposed interferometer is simple and it is easier to measure position-dependent instantaneous velocity using the ‘position- and magnitude-dependent shift-in-intensity profile’ obtained from the two sampled-interferograms. The advantage of the self-reference interferometer is that the test beam travels twice inside the sample and so the signal strength is higher than in other interferometers. Preliminary results of the glass samples with linear thermo-optic coefficient and linear thermal expansion are reported. The thermal diffusivity value closely matches with the literature for the BK7 sample. Further, the improved method for quartz sample in which the knowledge of temperature profile, thermo-optic coefficient, and thermal expansion are not needed to estimate thermal diffusivity, is also discussed for the quartz sample.